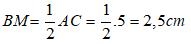50 Bài tập Hình chữ nhật Toán 8 mới nhất
Với 50 Bài tập Hình chữ nhật Toán lớp 8 mới nhất được biên soạn bám sát chương trình Toán 8 giúp các bạn học tốt môn Toán hơn.
Tài liệu gồm: 15 bài tập trắc nghiệm, 15 bài tập tự luận có lời giải và 20 bài tập vận dụng. Mời các bạn đón xem:
Bài tập Hình chữ nhật - Toán 8
I. Bài tập trắc nghiệm
Bài 1: Chọn đáp án đúng nhất trong các đáp án sau?
A. Hình chữ nhật là tứ giác có bốn cạnh bằng nhau.
B. Hình chữ nhật là tứ giác có bốn góc vuông.
C. Hình chữ nhật là tứ giác có hai góc vuông.
D. Các phương án trên đều không đúng.
Lời giải:
Định nghĩa: Hình chữ nhật là tứ giác có bốn góc vuông.
Chọn đáp án B.
Bài 2: Tìm câu sai trong các câu sau
A. Trong hình chữ nhật có hai đường chéo bằng nhau.
B. Trong hình chữ nhật có hai đường chéo cắt nhau tại trung điểm mỗi đường.
C. Trong hình chữ nhật có hai cạnh kề bằng nhau.
D. Trong hình chữ nhật, giao của hai đường chéo là tâm của hình chữ nhật đó
Lời giải:
Định lý trong hình chữ nhật
+ Hình chữ nhật có hai đường chéo bằng nhau.
+ Hình chữ nhật có hai đường chéo cắt nhau tại trung điểm mỗi đường.
+ Giao của hai đường chéo của hình chữ nhật là tâm của hình chữ nhật đó.
+ Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông
⇒ Đáp án C sai.
Chọn đáp án C.
Bài 3: Các dấu hiệu nhận biết sau, dấu hiệu nào nhận biết chưa đúng?
A. Hình bình hành có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình chữ nhật.
B. Tứ giác có ba góc vuông là hình chữ nhật.
C. Hình thang cân có một góc vuông là hình chữ nhật.
D. Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
Lời giải:
Dấu hiệu nhận biết hình chữ nhật:
+ Tứ giác có ba góc vuông là hình chữ nhật.
+ Hình thang cân có một góc vuông là hình chữ nhật.
+ Hình bình hành có một góc vuông là hình chữ nhật.
+ Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.
⇒ Hình bình hành có hai đường chéo cắt nhau tại trung điểm mỗi đường chưa đủ điều kiện để là hình chữ nhật.
Chọn đáp án A.
Bài 4: Khoanh tròn vào phương án sai
A. Trong tam giác vuông đường trung tuyến ứng với cạnh huyền và bằng nửa cạnh huyền.
B. Trong tam giác, đường trung tuyến với với một cạnh và bằng nửa cạnh ấy thì tam giác đó là tam giác vuông.
C. Trong tam giác vuông, đường trung tuyến ứng với cạnh góc vuông không bằng cạnh ấy.
D. Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền thì vuông góc với cạnh huyền.
Lời giải:
Định lý
+ Trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
+ Nếu một tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh ấy thì tam giác đó là tam giác vuông.
Chọn đáp án D.
Bài 5: Trong hình chữ nhật có kích thước lần lượt là 5cm và 12cm. Độ dài đường chéo của hình chữ nhật là ?
A. 17cm
B. 13cm
C. √119 cm
D. 12cm
Lời giải:
Độ dài của đường chéo hình chữ nhật bằng căn bậc hai tổng hai bình phương của hai kích thước hình chữ nhật
Do đó, độ dài đường chéo là √(52+122) = 13( cm )
Chọn đáp án B.
Bài 6: Cho hình chữ nhật ABCD có AB = 6cm và đường chéo BD = 10cm. Tính BC?
A. 8cm
B. 6cm
C. 7cm
D. 9cm
Lời giải:
Vì ABCD là hình chữ nhật nên AC = BD = 10cm.
Áp dụng định lí Pytago vào tam giác ABC ta có:
AC2 = AB2 + BC2
Suy ra: BC2 = AC2 - AB2 = 102 – 62 = 64
Nên BC = 8 cm
Chọn đáp án A
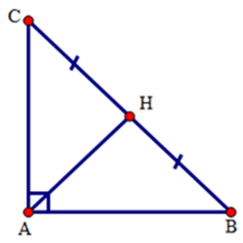
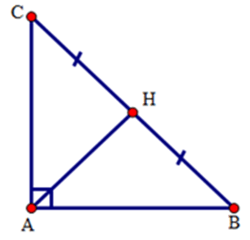
Bài 7: Cho tam giác ABC vuông tại B, gọi M là trung điểm của AC. Biết AB = 3cm, BC = 4cm. Tính BM?
A. 2cm
B. 3cm
C. 2,5cm
D. 3,5cm
Lời giải:
Áp dụng định lí Pytago vào tam giác vuông ABC ta có:
AC2 = AB2 + BC2 = 32 + 42 = 25
Suy ra: AC = 5cm
Tam giác ABC vuông tại B có BM là đường trung tuyến ứng với cạnh huyền AC nên:
Chọn đáp án
Bài 8: Cho hình thang vuông ABCD có ˆA+ˆD = 90o. Gọi M là trung điểm của AC và BM = 12 AC. Tìm khẳng định sai?
A. AC = BD
B. Tứ giác ABCD là hình chữ nhật
C. M là trung điểm của BD
D. AD = AB
Lời giải:
+ Xét tam giác ABC có đường trung tuyến BM và BM = 12 AC
Suy ra: tam giác ABC vuông tại B: ˆB = 90o
* Xét tứ giác ABCD có ˆA=ˆD=ˆB = 90o
Suy ra: tứ giác ABCD là hình chữ nhật (dấu hiệu nhận biết)
Theo tính chất của hình chữ nhật ta có:
AC = BD; AB = CD; AD = BC
Chọn đáp án D
Bài 9: Cho tam giác ABC vuông tại A. Gọi M , N, P lần lượt là trung điểm của AB; AC và BC. Hỏi tứ giác AMPN là hình gì? Chọn khẳng định đúng nhất?
A. Hình bình hành
B. Hình thang cân
C. Hình thang vuông
D. Hình chữ nhật
Lời giải:
* Ta có: M và P lần lượt là trung điểm của AB và BC nên MP là đường trung bình của tam giác.
Từ (1) và (2)suy ra: MP = AN .
* Xét tứ giác AMPN có: MP// AN ( vì MP // AC) và MP = AN
Suy ra: tứ giác AMPN là hình bình hành.
* Lại có ^BAC = 90o ( giả thiết)
Suy ra: tứ giác AMPN là hình chữ nhật.
Chọn đáp án D
Bài 10: Cho hình thang vuông ABCD vuông tại A và D, có AB = 6cm; DC = 9cm ; BC = 5cm. Tính AD?
A. 3cm
B. 4cm
C. 5cm
D. 6cm
Lời giải:
Kẻ BH vuông góc với CD tại H.
* xét tứ giác ABHD có: ˆA=ˆD=ˆH
Suy ra: tứ giác ABHD là hình chữ nhật
⇒ DH = AB = 6 (tính chất hình chữ nhật )
* HC = CD - DH = 9 – 6 = 3cm
* Áp dụng định lí Pytago vào tam giác vuông BCH có:
BH2 + HC2 = BC2
Suy ra: BH2 = BC2 – HC2 = 52 – 32 = 16
Nên BH = 4cm
* Vì ABHD là hình chữ nhật nên AD = BH = 4cm
Chọn đáp án B
Bài 11: Độ dài đường trung tuyến ứng với cạnh huyền của tam giác vuông có các cạnh góc vuông bằng 6cm, 8cm là:
A. 10cm
B. 9cm
C. 5cm
D. 8cm
Lời giải:
Áp dụng định lý Pytago cho tam giác ABC vuông tại A ta có:
BC2 = AC2 + AB2 hay BC2 = 62 + 82
⇒ BC2 = 100. Suy ra BC = 10 (cm)
Do AH là đường trung tuyến ứng với cạnh huyền BC nên
AH = BC : 2 = 10 : 2 = 5cm
Đáp án cần chọn là: C
Bài 12: Độ dài đường trung tuyến ứng với cạnh huyền của tam giác vuông có các cạnh góc vuông bằng 5cm, 12cm là:
A. 6,5cm
B. 6cm
C. 13cm
D. 10cm
Lời giải:
Áp dụng định lý Pytago cho tam giác ABC vuông tại A ta có:
BC2 = AC2 + AB2 hay BC2 = 52 + 122
⇒ BC2 = 169. Suy ra BC = 13 (cm)
Do AH là đường trung tuyến ứng với cạnh huyền BC nên
AH = BC : 2 = 13 : 2 = 6,5cm
Đáp án cần chọn là: A
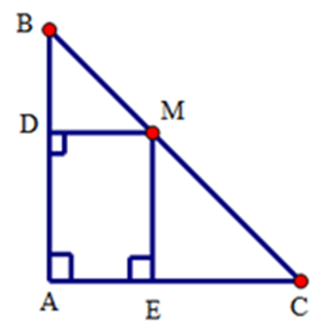
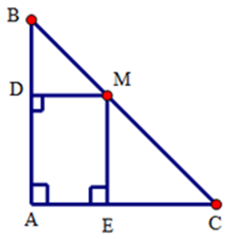
Bài 13: Cho tam giác ABC vuông tại A, AC = 6cm, điểm M thuộc cạnh BC. Gọi D, E theo thứ tự là các chân đường vuông góc kẻ từ M đến AB, AC. Chu vi của tứ giác ADME bằng:
A. 6cm
B. 36cm
C. 18cm
D. 12cm
Lời giải:
+ Xét tứ giác ADME có 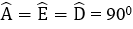
+ Xét tam giác DMB có 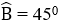
+ Do ADME là hình chữ nhật nên chu vi ADME là:
(AD + DM).2 = (AD + BD).2 = 6.2 = 12 cm
Vậy chu vi ADME là 12cm
Đáp án cần chọn là: D
Bài 14: Cho tam giác ABC vuông tại A, AC = 8cm, điểm M thuộc cạnh BC. Gọi D, E theo thứ tự là các chân đường vuông góc kẻ từ M đến AB, AC. Chu vi của tứ giác ADME bằng:
A. 16cm
B. 38cm
C. 18cm
D. 12cm
Lời giải:
+ Xét tứ giác ADME có 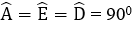
+ Xét tam giác DMB có 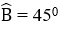
+ Do ADME là hình chữ nhật nên chu vi ADME là:
(AD + DM).2 = (AD + BD).2 = 8.2 = 16 cm
Vậy chu vi ADME là 12cm
Đáp án cần chọn là: A
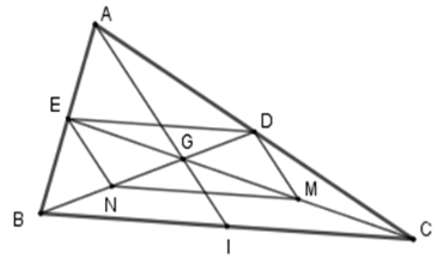
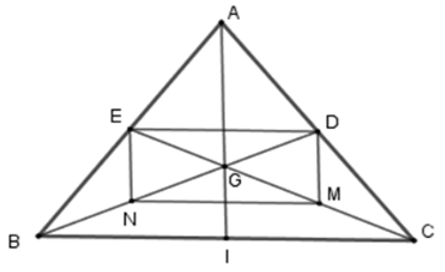
Bài 15: Cho tam giác ABC với ba trung tuyến AI, BD, CE đồng quy tại G. M và N lần lượt là trung điểm của GC và GB.
1. Tứ giác MNED là hình gì?
A. Hình chữ nhật
B. Hình bình hành
C. Hình thang cân
D. Hình thang vuông
Lời giải:
+ Xét tam giác ABC có E là trung điểm AB; D là trung điểm AC nên ED là đường trung bình của tam giác ABC ⇒ ED // BC; ED = 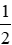
+ Xét tam giác GBC có N là trung điểm của GB; M là trung điểm GC nên MN là đường trung bình của tam giác GBC. ⇒ MN // BC; MN = 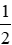
Từ (1), (2) ⇒ MN // ED, MN = ED nên tứ giác MNED là hình bình hành (dấu hiệu nhận biết)
Đáp án cần chọn là: B
2. Để MNED là hình chữ nhật thì tam giác ABC cần có điều kiện:
A. ΔABC đều
B. ΔABC vuông tại A
C. ΔABC cân tại A
D. ΔABC vuông cân tại A
Lời giải
+ Xét tam giác ABG có EN là đường trung bình nên EN // AG hay EN // AI.
+ Để hình bình hành MNED là hình chữ nhật thì 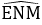
+ Lại có EN // AI suy ra AI ⊥ BC
Xét tam giác ABC có AI vừa là đường cao vừa là trung tuyến nên ΔABC cân tại A.
Đáp án cần chọn là: C
II. Bài tập tự luận có lời giải
Bài 1: Chứng minh rằng:
a) Giao điểm của hai đường chéo của hình chữ nhật là tâm đối xứng của hình chữ nhật đó.
b) Hai đường thẳng đi qua trung điểm hai cặp cạnh đối của hình chữ nhật là hai trục đối xứng của hình chữ nhật đó.
Lời giải:
a)
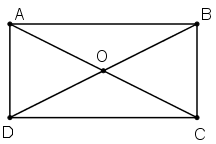
Giả sử ABCD là hình chữ nhật. Gọi O là giao điểm của AC và BD.
Theo tính chất đường chéo của hình chữ nhật ta có; hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường.
Vậy: OA = OC và OB= OD
Do đó, O là tâm đối xứng của hình chữ nhật đó.
b)
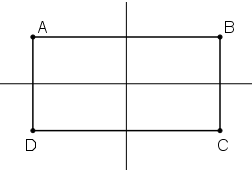
Áp dung tính chất: Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang cân đó.
ABCD là hình chữ nhật
⇒ ABCD là hình thang cân (hai đáy AB và CD)
⇒ Đường thẳng đi qua trung điểm AB và CD là trục đối xứng ABCD.
Tương tự vậy: ABCD cũng là hình thang cân với hai đáy AD và BC
⇒ Đường thẳng đi qua trung điểm AD và BC là trục đối xứng của ABCD.
Vậy ta có điều phải chứng minh.
Bài 2 Cho hình bình hành ABCD. Các tia phân giác của các góc A, B, C, D cắt nhau như trên hình 91. Chứng minh rằng EFGH là hình chữ nhật.
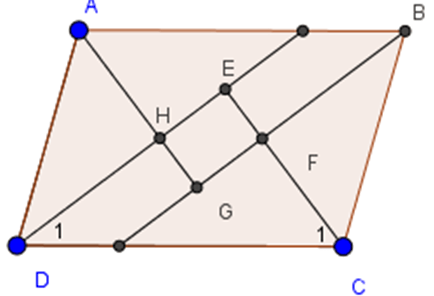
Hướng dẫn giải chi tiết:
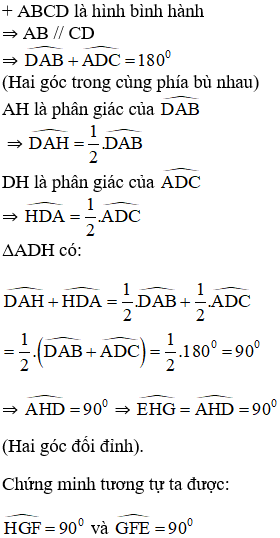
Bài 3 Điền vào chỗ trống, biết rằng a, b là độ dài của các cạnh, d là độ dài đường chéo của một hình chữ nhật.
| a | 5 | .... | √13 |
| b | 12 | √6 | .... |
| d | .... | √10 | 7 |
Lời giải:
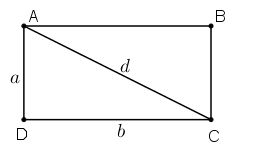
Trong hình chữ nhật ABCD ta luôn có
![]()
Do đó áp dụng định lý Py-ta-go ta có: d2 = a2 + b2.
Vậy :
- Cột thứ hai:
d2 = a2 + b2 = 52 + 122 = 25 + 144 = 169 nên d = 13
- Cột thứ ba:
a2 + b2 = d2 ⇒ a2 = d2 – b2 = (√10)2-(√6)2 = 4 nên a = 2
- Cột thứ tư:
a2 + b2 = d2 ⇒ b2 = d2 – a2 = 72 – (√13)2 = 36 nên b = 6.
Vậy ta có bảng sau:
| a | 5 | 2 | √13 |
| b | 12 | √6 | 6 |
| d | 13 | √10 | 7 |
Bài 4 Tính độ dài đường trung tuyến ứng với cạnh huyền của một tam giác vuông có cạch góc vuông bằng 7cm và 24 cm.
Lời giải:
Gọi a là độ dài cạnh huyền của tam giác vuông.
Theo định lý Pi-ta-go ta có:
a2 = 72 + 242 = 625
⇒ a = 25cm
⇒ Độ dài trung tuyến ứng với cạnh huyền bằng: a2=252 = 12,5 (cm).
Cho tam giác ABC, đường cao AH. Gọi I là trung điểm của AC, E là điểm đối xứng với H qua I. Tứ giác AHCE là hình gì? Vì sao?
Lời giải:
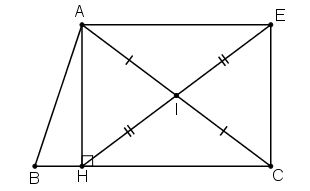
I là trung điểm của AC ⇒ IA = IC.
E đối xứng với H qua I ⇒ IE = IH
⇒ AC ∩ HE = I là trung điểm của AC và HE
⇒ AHCE là hình bình hành (dấu hiệu nhận biết 4)
Lại có : Ĥ = 90º
⇒ AHCE là hình chữ nhật (đpcm).
Bài 5 Các câu sau đúng hay sai?
a) Nếu tam giác ABC vuông tại C thì điểm C thuộc đường tròn có đường kính là AB (h.88)
b) Nếu điểm C thuộc đường tròn có đường kính là AB (C khác A và B) thì tam giác ABC vuông tại C (h.89).
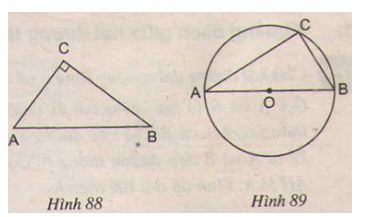
Lời giải:
a) Đúng
Gọi O là trung điểm của AB.
Ta có CO là trung tuyến ứng với cạnh huyền nên
⇒ OC = AB2 = OA = OB.
⇒ A, B, C cùng thuộc đường tròn bán kính OA.
Tâm O là trung điểm của AB nên AB là đường kính.
Vậy C thuộc đường tròn đường kính AB.
b) Đúng
Gọi O là tâm đường tròn.
⇒ OA = OB = OC = R
AB là đường kính nên AB = 2R.
Tam giác ABC có CO là trung tuyến và CO = AB2
⇒ ΔABC vuông tại C.
Bài 6 Chứng minh rằng:
a) Giao điểm của hai đường chéo của hình chữ nhật là tâm đối xứng của hình chữ nhật đó.
b) Hai đường thẳng đi qua trung điểm hai cặp cạnh đối của hình chữ nhật là hai trục đối xứng của hình chữ nhật đó.
Lời giải:
a)
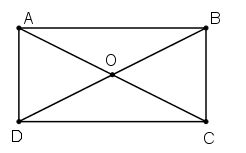
Giả sử có ABCD là hình chữ nhật có AC ∩ DB = O.
ABCD là hình chữ nhật
⇒ ABCD là hình bình hành
⇒ O là tâm đối xứng của ABCD.
b)
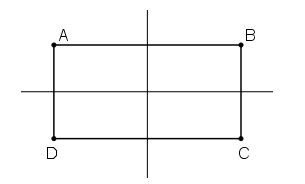
ABCD là hình chữ nhật
⇒ ABCD là hình thang cân (2 đáy AB và CD)
⇒ Đường thẳng đi qua trung điểm AB và CD là trục đối xứng ABCD.
Tương tự vậy: ABCD cũng là hình thang cân với 2 đáy AD và BC
⇒ Đường thẳng đi qua trung điểm AD và BC là trục đối xứng của ABCD.
Vậy ta có điều phải chứng minh.
Bài 7 Tìm x trên hình 90
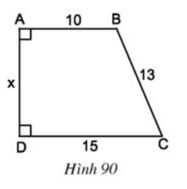
Lời giải:
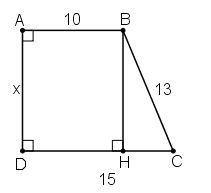
Kẻ BH ⊥ CD
⇒ ABHD là hình chữ nhật
⇒ ABHD là hình bình hành
⇒ DH = AB = 10 ⇒ HC = CD – DH = 5.
Δ BHC vuông tại H có:
ABHD là hình bình hành
⇒ AD = BH = 12
hay x = 12.
Bài 8. Một đội công nhân đang trồng cây trên đoạn đường AB thì gặp chướng ngại vật che lấp tầm nhìn (h.92). Đội đã dựng các điểm C, D, E như trên hình vẽ rồi trồng cây tiếp trên đoạn đường EF vuông góc với DE. Vì sao AB và EF cùng nằm trên một đường thẳng?
Lời giải:

Bài 9 Cho ΔABC vuông cân tại C. Trên cạnh AC, BC lấy lần lượt các điểm P, Q sao cho AP = CQ. Từ điểm P vẽ PM // BC (M thuộc AB). Chứng minh rằng tứ giác PCQM là hình chữ nhật.
Hướng dẫn:

Ta có ΔABC vuông cân ⇒ˆA=45∘
⇒ ΔAPM vuông cân
⇒ AP = PM
Theo giả thiết AP = CQ ⇒ PM = CQ
Lại có PM // CQ ⇒ tứ giác PMCQ là hình bình hành.
Mà ˆC=90∘ ⇒ tứ giác PMCQ là hình chữ nhật.
III. Bài tập vận dụng
Bài 1 Cho tứ giác ABCD có AC ⊥ BD. Gọi E, F, G, H lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh rằng tứ giác EFGH là hình chữ nhật.
Bài 2 Cho ΔABC vuông tại A, AB < AC, đường cao AH. Lấy điểm E trên cạnh AC sao cho AE = AB. Gọi I là trung điểm của BE, kẻ EK ⊥ BC (K ∈ BC), EN ⊥ AH (N ∈ AH)
a) Chứng minh rằng tứ giác NEKH là hình chữ nhật.
b) ^IHA=^IHC
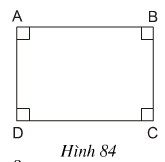
Bài 3 Chứng minh rằng hình chữ nhật ABCD trên hình 84 cũng là một hình bình hành, một hình thang cân.
Bài 4 Với một chiếc compa, ta sẽ kiểm tra được hai đoạn thẳng bằng nhau hay không bằng nhau. Bằng compa, để kiểm tra tứ giác ABCD có là hình chữ nhật hay không, ta làm thế nào ?
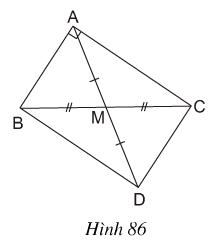
Bài 5 Cho hình 86:
a) Tứ giác ABDC là hình gì ? Vì sao ?
b) So sánh các độ dài AM và BC.
c) Tam giác vuông ABC có AM là đường trung tuyến ứng với cạnh huyền. Hãy phát biểu tính chất tìm được ở câu b) dưới dạng một định lý.
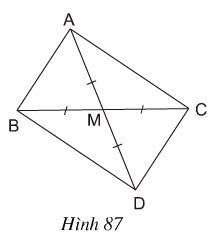
Bài 6 Cho hình 87:
a) Tứ giác ABDC là hình gì ? Vì sao ?
b) Tam giác ABC là tam giác gì ?
c) Tam giác ABC có đường trung tuyến AM bằng nửa cạnh BC. Hãy phát biểu tính chất tìm được ở câu b) dưới dạng một định lý.
Bài 7 Một đội công nhân đang trồng cây trên đoạn đường AB thì gặp chướng ngại vật che lấp tầm nhìn. Độ đã dựng các điểm C, D, E như trên hình vẽ rồi trồng cây tiếp trên đoạn đường EF vuông góc với DE. Vì sao AB và EF cùng nằm trên một đường thẳng.

Bài 8 Tìm x trên hình vẽ dưới đây.

Bài 9 Cho hình thang cân ABCD có AB // CD; AB < CD. Đường cao AH. Gọi M, N lần lượt là trung điểm của AD và BC. Tính độ dài đoạn MN biết HC = 5cm.
Bài 10 Cho ΔABC vuông tại A, từ điểm D trên cạnh huyền BC vẽ DE ⊥ AB, DF ⊥ AC. Gọi I là trung điểm của EF. Chứng minh ba điểm A, I, D thẳng hàng.
Bài 11 Cho ΔABC cân tại A. Từ điểm D trên đáy BC kẻ đường vuông góc với BC cắt AB ở E và AC ở F. Vẽ các hình chữ nhật DBHE và CDFK. Chứng minh rằng A là trung điểm của HK
Bài 12 Cho ΔABC cân tại A, đường cao BH. Từ điểm M trên cạnh BC kẻ MP ⊥ AB, MQ ⊥ AC. Chứng minh rằng MP + MQ = BH.
Bài 13 Cho ΔABC có góc B nhọn và ˆB=2ˆC. Kẻ đường cao AH, trên tia đối của tia BA lấy điểm D sao cho BD = BH, gọi I là giao điểm của DH và BC. Chứng minh rằng:
a) AI = IC
b) AD = HC
Bài 14 Cho hình thang cân ABCD có AB // CD, hai đường chéo AC và BD vuông góc với nhau. Chứng minh rằng chiều cao BH bằng đường trung bình MN.
Bài 15 Cho ΔABC vuông tại A, đường cao AH, trung tuyến AM và phân giác AD. Chứng minh rằng:
a) ^HAB=^MAC
b) AD là tia phân giác của ^HAM
c) IH ⊥ HK
Xem thêm các bài Bài tập Toán lớp 8 hay, chi tiết khác:
Xem thêm các chương trình khác:
- Tóm tắt tác phẩm Ngữ văn 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Soạn văn 8 (hay nhất) | Để học tốt Ngữ văn lớp 8 (sách mới)
- Soạn văn 8 (ngắn nhất) | Để học tốt Ngữ văn lớp 8 (sách mới)
- Văn mẫu lớp 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Tác giả - tác phẩm Ngữ văn 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Hóa học 8
- Giải sbt Hóa học 8
- Giải vở bài tập Hóa học 8
- Lý thuyết Hóa học 8
- Các dạng bài tập Hóa học lớp 8
- Giải sgk Vật Lí 8
- Giải sbt Vật Lí 8
- Lý thuyết Vật Lí 8
- Giải vở bài tập Vật lí 8
- Giải sgk Tiếng Anh 8 (sách mới) | Giải bài tập Tiếng Anh 8 Học kì 1, Học kì 2
- Giải sgk Tiếng Anh 8 | Giải bài tập Tiếng Anh 8 Học kì 1, Học kì 2 (sách mới)
- Giải sbt Tiếng Anh 8 (sách mới) | Sách bài tập Tiếng Anh 8
- Giải sbt Tiếng Anh 8 (thí điểm)
- Giải sgk Tin học 8 | Giải bài tập Tin học 8 Học kì 1, Học kì 2 (sách mới)
- Giải sgk Lịch Sử 8 | Giải bài tập Lịch sử 8 Học kì 1, Học kì 2 (sách mới)
- Lý thuyết Lịch sử 8 (sách mới) | Kiến thức trọng tâm Lịch sử 8
- Giải vở bài tập Lịch sử 8
- Giải Tập bản đồ Lịch sử 8
- Đề thi Lịch Sử 8
- Giải vở bài tập Sinh học 8
- Giải sgk Sinh học 8
- Lý thuyết Sinh học 8
- Giải sgk Giáo dục công dân 8 | Giải bài tập Giáo dục công dân 8 Học kì 1, Học kì 2 (sách mới)
- Lý thuyết Giáo dục công dân 8 (sách mới) | Kiến thức trọng tâm GDCD 8
- Lý thuyết Địa Lí 8 (sách mới) | Kiến thức trọng tâm Địa Lí 8
- Giải sgk Địa Lí 8 | Giải bài tập Địa Lí 8 Học kì 1, Học kì 2 (sách mới)
- Giải Tập bản đồ Địa Lí 8
- Đề thi Địa lí 8