50 Bài tập Những hằng đẳng thức đáng nhớ Toán 8 mới nhất

Bài tập Những hằng đẳng thức đáng nhớ

I. Bài tập trắc nghiệm

Bài 1: Điền vào chỗ trống: A = ($\frac{1}{2}$x - y )² = $\frac{1}{4}$x² - ... + y²

A. 2xy   

B. xy

C. - 2xy   

D. $\frac{1}{2}$ xy

Lời giải:

Áp dụng hằng đẳng thức (a - b)² = a² - 2ab + b².

Khi đó ta có A = ( $\frac{1}{2}$x - y )² = $\frac{1}{4}$x² - 2.$\frac{1}{2}$x.y + y² = $\frac{1}{4}$x² - xy + y².

Suy ra chỗ trống cần điền là xy.

Chọn đáp án B.

Bài 2: Điều vào chỗ trống: ... = ( 2x - 1 )( 4x² + 2x + 1 ).

   A. 1 - 8x³.

   B. 1 - 4x³.

   C. x³ - 8.

   D. 8x³ - 1.

Lời giải:

Áp dụng hằng đẳng thức a³ - b³ = ( a - b )( a² + ab + b² )

Khi đó ta có ( 2x - 1 )( 4x² + 2x + 1 )

= ( 2x - 1 )[ ( 2x )² + 2x.1 + 1 ]

= ( 2x )³ - 1 = 8x³ - 1.

Suy ra chỗ trống cần điền là 8x³ - 1.

Chọn đáp án D.

Bài 3: Tính giá trị của biểu thức A = 8x³ + 12x²y + 6xy² + y³ tại x = 2 và y = -1.

A. 1   

B. 8

C. 27  

D. -1

Lời giải:

Áp dụng hằng đẳng thức ( a + b )³ = a³ + 3a²b + 3ab² + b³.

Khi đó ta có:

A = 8x³ + 12x²y + 6xy² + y³ 

= ( 2x )³ + 3.( 2x )².y + 3.( 2x ).y² + y³ 

= ( 2x + y )³

Với x = 2 và y = -1 ta có A = ( 2.2 - 1 )³ = 3³ = 27.

Chọn đáp án C.

Bài 4: Tính giá trị của biểu thức A = 35² - 700 + 10².

A. 25².   

B. 15².

C. 45².   

D. 20².

Lời giải:

Ta có A = 35² - 700 + 10² = 35² - 2.35.10 + 10²

Áp dụng hằng đẳng thức ( a - b )² = a² - 2ab + b².

Khi đó A = ( 35 - 10 )² = 25².

Chọn đáp án A.

Bài 5: Giá trị của x thỏa mãn 2x² - 4x + 2 = 0 là ?

A. x = 1.   

B. x = - 1.

C. x = 2.   

D. x = - 2.

Lời giải:

Ta có 2x² - 4x + 2 = 0

⇔ 2( x² - 2x + 1 ) = 0        ( 1 )

Áp dụng hằng đẳng thức ( a - b )² = a² - 2ab + b²

Khi đó ta có ( 1 ) ⇔ 2( x - 1 )² = 0

⇔ x - 1 = 0

⇔ x = 1.

Chọn đáp án A.

Bài 6: 

Lời giải:

Áp dụng hằng đẳng thức đáng nhớ: 

Ta được:

Chọn đáp án A

Bài 7: Điền vào chỗ chấm:

Lời giải:

Chọn đáp án C

Bài 8: Rút gọn biểu thức: A = (x – 2y).(x² + 2xy + y²) - (x + 2y). (x² – 2xy + y²)

A. 2x³    

B. -16y³

C. 16y³    

D. –2x³

Lời giải:

Áp dụng hằng đẳng thức:

a³ – b³ = (a – b).(a² + ab + b²) và a³ + b³ = (a + b).(a² – ab + b²) ta được:

A = (x – 2y). (x² + 2xy + y²) - (x + 2y). (x² – 2xy + y²)

A = x³ – (2y)³ - [x³ + (2y)³]

A = x³ – 8y³ – x³ – 8y³ = -16y³

Chọn đáp án B

Bài 9: Tìm x biết x² – 16 + x(x – 4) = 0

A. x = 2 hoặc x = - 4.

B. x = 2 hoặc x = 4.

C. x = -2 hoặc x = - 4.

D. x = -2 hoặc x = 4.

Lời giải:

Ta có: x² – 16 + x(x – 4) = 0

⇔ (x + 4). (x - 4) + x.(x – 4) = 0

⇔ (x + 4 + x).(x - 4) = 0

⇔ (2x + 4). (x - 4) = 0

⇔ 2x + 4 = 0 hoặc x – 4 = 0

* Nếu 2x + 4 = 0 thì x = -2

* Nếu x – 4 =0 thì x = 4

Vậy x = -2 hoặc x = 4.

Chọn đáp án D

Bài 10: Rút gọn biểu thức A = (x + 2y ).(x - 2y) - (x – 2y)²

A. 2x² + 4xy    

B. – 8y² + 4xy

C. - 8y²    

D. – 6y² + 2xy

Lời giải:

Ta có: A = (x + 2y ). (x - 2y) - (x – 2y)²

A = x² – (2y)² – [x² – 2.x.2y +(2y)² ]

A = x² – 4y² – x² + 4xy - 4y²2

A = -8y² + 4xy

Chọn đáp án B

Bài 11: Chọn câu đúng

A. (c + d)² – (a + b)² = (c + d + a + b)(c + d – a + b)

B. (c – d)² – (a + b)² = (c – d + a + b)(c – d – a + b)

C. (a + b + c – d)(a + b – c + d) = (a + b)² – (c – d)²

D. (c – d)² – (a – b)² = (c – d + a – b)(c – d – a – b)

Lời giải:

Ta có:

(c + d)² – (a + b)² = (c + d + a + b)(c + d – (a + b)) = (c + d + a + b)(c + d – a – b) nên A sai

(c – d)² – (a + b)² = (c – d + a + b)[c – d – (a + b)] = (c – d + a + b)(c – d – a – b) nên B sai

(c – d)² – (a – b)² = (c – d + a – b)(c – d – (a – b)) = (c – d + a – b)(c – d – a + b) nên D sai

(a + b + c – d)(a + b – c + d) = [(a + b) + (c – d)][(a + b) – (c – d)] = (a + b)² – (c – d)² nên C đúng

Đáp án cần chọn là: C

Bài 12: Chọn câu đúng

A. 4 – (a + b)² = (2 + a + b)(2 – a + b)

B. 4 – (a + b)² = (4 + a + b)(4 – a – b)

C. 4 – (a + b)² = (2 + a – b)(2 – a + b)

D. 4 – (a + b)² = (2 + a + b)(2 – a – b)

Lời giải

Ta có 4 – (a + b)² = 2² – (a + b)² 

= (2 + a + b)[2 – (a + b)]

= (2 + a + b)(2 – a – b)

Đáp án cần chọn là: D

Bài 13: Rút gọn biểu thức A = (3x – 1)² – 9x(x + 1) ta được

A. -15x + 1 

B. 1            

C. 15x + 1            

D. – 1

Lời giải: Ta có

A = (3x – 1)² – 9x(x + 1)

= (3x)² – 2.3x.1 + 1 – (9x.x + 9x)

= 9x² – 6x + 1 – 9x² – 9x

 = -15x + 1

Đáp án cần chọn là: A

Bài 14: Rút gọn biểu thức A = 5(x + 4)² + 4(x – 5)² – 9(4 + x)(x – 4), ta được:

A. 342     

B. 243    

C. 324   

D. -324

Lời giải

Ta có

A = 5(x + 4)² + 4(x – 5)² – 9(4 + x)(x – 4)

= 5(x² + 2.x.4 + 16) + 4(x² – 2.x.5 + 5²) – 9(x² – 4²)

= 5(x² + 8x + 16) + 4(x² – 10x + 25) – 9(x² – 4²)

= 5x² + 40x + 80 + 4x² – 40x + 100 – 9x² + 144

= (5x² + 4x² – 9x²) + (40x – 40x) + (80 +100 + 144)

= 324

Đáp án cần chọn là: C

Bài 15: Rút gọn biểu thức B = (2a – 3)(a + 1) – (a – 4)² – a(a + 7) ta được

A. 0            

B. 1            

C. 19          

D. – 19

Lời giải

B = (2a – 3)(a + 1) – (a – 4)² – a(a + 7)

= 2a² + 2a – 3a – 3 – (a² – 8a + 16) – (a² + 7a)

= 2a² + 2a – 3a – 3 – a² + 8a – 16 – a² – 7a

= - 19

Đáp án cần chọn là: D

Bài 16: Cho B = (x² + 3)² – x²(x² + 3) – 3(x + 1)(x – 1). Chọn câu đúng.

A. B < 12   

B. B > 13   

C. 12 < B< 14

D. 11 < B < 13

Lời giải

B = (x² + 3)² – x²(x² + 3) – 3(x + 1)(x – 1).

= (x²)² +2.x².4 + 3² – (x².x² + x².3) – 3(x² – 1)       

= x⁴ + 6x² + 9 – x⁴ – 3x² – 3x² + 3 = 12

Đáp án cần chọn là: D

Bài 17: Cho 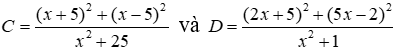. Tìm mối quan hệ giữa C và D.

A. D = 14C + 1

B. D = 14C 

C. D = 14C – 1

D. D = 14C – 2

Lời giải

Ta có:

Vậy D = 29; C = 2 suy ra D = 14C + 1 (do 29 = 14.2 + 1)

Đáp án cần chọn là: A

Bài 18: Cho M = 4(x + 1)² +  (2x + 1)² – 8(x – 1)(x + 1) – 12x và N = 2(x – 1)² – 4(3 + x)² + 2x(x + 14).

Tìm mối quan hệ giữa M và N

A. 2N – M = 60

B. 2M – N = 60

C. M> 0, N < 0

D. M > 0, N > 0

Lời giải

Ta có

M = 4(x + 1)² +  (2x + 1)² – 8(x – 1)(x + 1) – 12

= 4(x² + 2x + 1) + (4x² + 4x + 1) – 8(x² – 1) – 12x

= 4x² + 8x + 4 + 4x² + 4x + 1 – 8x² +8 – 12x

= (4x² + 4x² – 8x²) + (8x + 4x – 12x) + 4 + 1 +8

= 13

N = 2(x – 1)² – 4(3 + x)² + 2x(x + 14)

= 2(x² – 2x + 1) – 4(9 + 6x + x²) + 2x² + 28x

= 2x² – 4x + 2 – 36 – 24x – 4x² + 2x² + 28x

= (2x² +2x² – 4x²) + (-4x – 24x + 28x) + 2 – 36

= -34

Suy ra M = 13, N = -34 ⇔ 2M – N = 60

Đáp án cần chọn là: B

Bài 19: Có bao nhiêu giá trị x thỏa mãn (2x – 1)² – (5x – 5)² = 0

A. 0            

B. 1            

C. 2            

D. 3

Lời giải

Vậy có hai giá trị của x thỏa mãn yêu cầu

Đáp án cần chọn là: C

Bài 20: Có bao nhiêu giá trị x thỏa mãn (2x + 1)² – 4(x + 3)² = 0

A. 0            

B. 1            

C. 2            

D. 3

Lời giải

Ta có:

Vậy có một giá trị của x thỏa mãn yêu cầu.

Đáp án cần chọn là: B

II. Bài tập tự luận

Bài 1: Viết các biểu thức sau dưới dạng bình phương của một tổng hoặc một hiệu:

a,	b,
c,	d,
e,	f,

Lời giải:

a, 

b, 

c, 

d,  

e, 

f,

Bài 2: Tính giá trị của biểu thức:

a,  tại a = 2, b = 3

b,  tại 

c,  tại x= 5

Lời giải:

a, Thay a = 2, b = 3 vào  có: 

b, Có 

Thay  có: 

c, Có 

Thay x = 5 có: 

Bài 3: Tính:

a,  

b, 

Lời giải:

a,

b,

Bài 4 

Viết các biểu thức sau dưới dạng bình phương của một tổng hoặc một hiệu:

a) x² + 2x + 1

b) 9x² + y² + 6xy;

c) 25a² + 4b² – 20ab;

d) x² – x + $\frac{1}{4}$

Đáp án và hướng dẫn giải:

a) x² + 2x + 1 = x²+ 2.x.1 + 12

= (x + 1)²

b) 9x² + y²+ 6xy = (3x)² + 2.3. x.y + y.2 = (3x + y)²

c) 25a² + 4b²– 20ab = (5a)² – 2.5a.2b + (2b)² = (5a – 2b)²

Hoặc 25a² + 4b² – 20ab = (2b)² – 2.2b.5a + (5a)² = (2b – 5a)²

d) x² – x + $\frac{1}{4}$

= x² – 2.x.$\frac{1}{2}$+ ($\frac{1}{2}$)²

=(x - $\frac{1}{2}$)²

Hoặc x² – x + $\frac{1}{4}$

= $\frac{1}{4}$- x + x2 =($\frac{1}{2}$)² – 2.$\frac{1}{2}$ x + x² = ($\frac{1}{2}$ - x⁾²

Bài 5

Chứng minh rằng:

(10a + 5)² = 100a . (a + 1) + 25.

Từ đó em hãy nêu cách tính nhẩm bình phương của một số tự nhiên có tận cùng bằng chữ số 5.

Áp dụng để tính: 25², 35², 65², 75².

Đáp án và hướng dẫn giải:

Ta có: (10a + 5)² = (10a)² + 2.10a.5 + 5²

= 100a² + 100a + 25

= 100a(a + 1) + 25.

Cách tính nhẩm bình thường của một số tận cùng bằng chữ số 5;

Ta gọi a là số chục của số tự nhiên có tận cùng bằng 5 => số đã cho có dạng 10a + 5 và ta được

(10a + 5)² = 100a(a + 1) + 25

Vậy để tính bình phương của một số tự nhiên có tận cùng bởi chữ số 5 ta tính tích a(a + 1) rồi viết 25 vào bên phải.

Áp dụng;

Để tính 25² ta tính 2(2 + 1) = 6 rồi viết tiếp 25 vào bên phải ta được 625.

Để tính 35² ta tính 3(3 + 1) = 12 rồi viết tiếp 25 vào bên phải ta được 1225.

65² = (10.6 + 5)²= 100.6(6+1) +25= 600.7 +25 =4200 +25= 4225

75² =(10.7+5)2 = 100.7(7+1) +25 = 700.8 +25=5600 +25 = 5625

Bài 6

Hãy tìm cách giúp bạn An khôi phục lại những hằng đẳng thức bị mực làm nhòe đi một số chỗ:

a) x² + 6xy + … = (… + 3y)²;

b) … – 10xy + 25y² = (… – …)²;

Hãy nêu một số đề bài tương tự.

Đáp án và hướng dẫn giải:

a) x² + 6xy + … = (… + 3y)² nên x² + 2x . 3y + … = (…+3y)²

= x² + 2x . 3y + (3y)² = (x + 3y)²

Vậy: x² + 6xy +9y² = (x + 3y)²

b) …-2x . 5y + (5y)2 = (… – …)²;

x² – 2x . 5y + (5y)² = (x – 5y)²

Vậy: x² – 10xy + 25y² = (x – 5y)²

Bài 7:

Tính diện tích phần hình còn lại mà không cần đo.

Từ một miếng tôn hình vuông có cạnh bằng a + b, bác thợ cắt đi một miếng cũng hình vuông có cạnh bằng a – b (cho a > b). Diện tích phần hình còn lại là bao nhiêu? Diện tích phần hình còn lại có phụ thuộc vào vị trí cắt không?

Đáp án và hướng dẫn giải bài:

Diện tích của miếng tôn là (a + b)²

Diện tích của miếng tôn phải cắt là (a – b)².

Phần diện tích còn lại là (a + b)2 – (a – b)².

Ta có: (a + b)² – (a – b)² = a² + 2ab + b² – (a² – 2ab + b²)

= a² + 2ab + b² – a² + 2ab – b²

= 4ab

Vậy phần diện tích hình còn lại là 4ab và không phụ thuộc vào vị trí cắt.

Bài 8: 

Nhận xét sự đúng, sai của kết quả sau:

x² + 2xy + 4y² = (x + 2y)²

Đáp án và hướng dẫn giải:

Nhận xét sự đúng, sai:

Ta có: (x + 2y)² = x² + 2 . x . 2y + 4y²

= x² + 4xy + 4y²

Nên kết quả x² + 2xy + 4y² = (x + 2y)² sai.

Bài 9: 

Viết các đa thức sau dưới dạng bình phương của một tổng hoặc một hiệu:

a) 9x² – 6x + 1;

b) (2x + 3y)² + 2.(2x + 3y) + 1.

Hãy nêu một đề bài tương tự.

Đáp án và hướng dẫn giải:

a) 9x² – 6x + 1 = (3x)² – 2 . 3x . 1 + 1² = (3x – 1)²

Hoặc 9x² – 6x + 1 = 1 – 6x + 9x² = (1 – 3x)²

b) (2x + 3y) = (2x + 3y)² + 2 . (2x + 3y) . 1 + 1²

= [(2x + 3y) + 1]²

= (2x + 3y + 1)²

Đề bài tương tự. Chẳng hạn:

1 + 2(x + 2y) + (x + 2y)²

4x² – 12x + 9…

16x² y⁴ – 8xy² +1

Bài 10

Tính nhanh:

a) 1012; b) 1992; c) 47.53.

Đáp án và hướng dẫn giải:

a) 101² = (100 + 1)² = 100² + 2 . 100 + 1 = 10201

b) 199²= (200 – 1)² = 200² – 2 . 200 + 1 = 39601

c) 47.53 = (50 – 3)(50 + 3) = 50² – 3² = 2500 – 9 = 2491.

III. Bài tập vận dụng

Bài 1:

Chứng minh rằng:

(a + b)² = (a – b)² + 4ab;

(a – b)² = (a + b)² – 4ab.

Áp dụng:

a) Tính (a – b)², biết a + b = 7 và a . b = 12.

b) Tính (a + b)², biết a – b = 20 và a . b = 3.

Bài 2:

Tính giá trị của biểu thức 49x² – 70x + 25 trong mỗi trường hợp sau:

a) x = 5;

b) x = 1/7.

Bài 3:

Tính:

a) (a + b + c)²; b) (a + b – c)²;

c) (a – b – c)²

Bài 4. Áp dụng hằng đẳng thức để tính nhanh

a)  =                     b) 29,9. 30,1 =

c)  – 2.31,8.21,8 +  =

Bài 5. Điền vào ô trống để trở thành hằng đẳng thức:

Ví  dụ : 36 + 24x + ………..=

Phân tích : 36 = và 24x = 2. 6x. 2, từ đó phần còn thiếu là  = 4

Đáp án : 36 + 24x + 4 = 

a)  + 20x + ……..  =

b) 16 + 24x + ……..= 

c)  – ……….  + 49 =   

d) …………- 42xy +  49 = 

e)    + ………..+ 4 = 

f) 4 +…………..+ 1 =

g) (2a +3b)(            –                +               ) = 8   + 27

h) (5x –    )(        +          20xy +               ) = 125 – 64

Bài 6. Viết mỗi biểu thức sau dưới dạng tổng của hai bình phương

Ví dụ :   – 2xy + 2 +2y +1 = (  – 2xy + ) + ( +2y +1) =  + 

a)  + 10x + 26 +  +2y =

b)  – 6z + 13 +  +4t =

c) 4 – 4xz + 1 + 2 -2z =

Bài 7. Tìm giá trị lớn nhất của biểu thức:

a) C = 4x –  + 3

Tìm giá trị nhỏ nhất của biểu thức:

a) A =  – 6x + 11

b) B =  – 4x +  – 8y + 6

Bài 8. Chứng minh các biểu thức sau luôn dương với mọi giá trị của biến

D =  – 8x +19 

Chứng minh các biểu thức sau luôn âm với mọi giá trị của biến

 E = – + 2x – 7 

Bài 9. Khai triển hằng đẳng thức dạng  và 

 =  + 2.A.B +                =  – 2.A.B +  

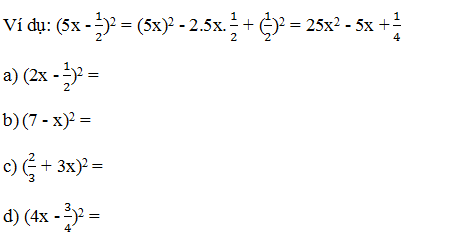
Bài 10. Khai triển hằng đẳng thức dạng  và 

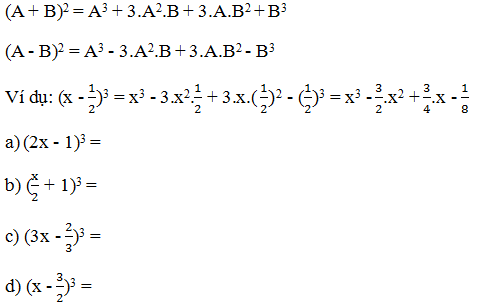
Xem thêm các bài Bài tập Toán lớp 8 hay, chi tiết khác:

Bài tập Nhân đơn thức với đa thức

Bài tập Những hằng đẳng thức đáng nhớ

Bài tập Phân tích đa thức thành nhân tử

Bài tập Chia đơn thức cho đơn thức

Bài tập Chia đa thức cho đơn thức

A. 2xyB. xyC. - 2xyD. 1/2 xyLời giải:Áp dụng hằng đẳng thức (a - b)² = a² - 2ab + b².Khi đó ta có A = ($\frac{1}{2}$x - y )² = $\frac{1}{4}$x² - 2.$\frac{1}{2}$x.y + y² = $\frac{1}{4}$x² - xy + y².Suy ra chỗ trống cần điền là xy.Chọn đáp án B.Bài 2: Điều vào chỗ trống: ... = ( 2x - 1 )( 4x² + 2x + 1 ).A. 1 - 8x³.B. 1 - 4x³.C. x³ - 8.D. 8x³ - 1.Lời giải:Áp dụng hằng đẳng thức a³ - b³ = ( a - b )( a² + ab + b² )Khi đó ta có ( 2x - 1 )( 4x² + 2x + 1 ) = ( 2x - 1 )[ ( 2x )² + 2x.1 + 1 ] =( 2x )³ - 1 = 8x³ - 1.Suy ra chỗ trống cần điền là 8x³ - 1.Chọn đáp án D.Bài 3: Tính giá trị cuả biểu thức A = 8x³ + 12x²y + 6xy² + y³ tại x = 2 và y = -1.A. 1B. 8C. 27D. -1Lời giải:Áp dụng hằng đẳng thức ( a + b )³ = a³ + 3a²b + 3ab² + b³.Khi đó ta có:A = 8x³ + 12x²y + 6xy² + y³ = ( 2x )³ + 3.( 2x )².y + 3.( 2x ).y² + y³ = ( 2x + y )³Với x = 2 và y = -1 ta có A = ( 2.2 - 1 )³ = 3³ = 27.Chọn đáp án C.Bài 4: Tính giá trị của biểu thức A = 35² - 700 + 10².A. 25².B. 15².C. 45².D. 20².Lời giải:Ta có A = 35² - 700 + 10² = 35² - 2.35.10 + 10²Áp dụng hằng đẳng thức ( a - b )² = a² - 2ab + b².Khi đó A = ( 35 - 10 )² = 25².Chọn đáp án A.Bài 5: Giá trị của x thỏa mãn 2x² - 4x + 2 = 0 là?A. x = 1.B. x = - 1.C. x = 2.D. 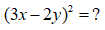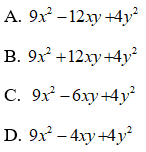x = - 2.Lời giải:Ta có 2x² - 4x + 2 = 0 ⇔ 2( x² - 2x + 1 ) = 0        ( 1 )Áp dụng hằng đẳng thức ( a - b )² = a² - 2ab + b²Khi đó ta có ( 1 ) ⇔ 2( x - 1 )² = 0 ⇔ x - 1 = 0 ⇔ x = 1.Chọn đáp án A.Bài 6: Lời giải:Áp dụng hằng đẳng thức đáng nhớ: 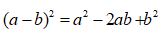Ta được: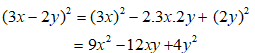Chọn đáp án  A.Bài 7: Điền vào chỗ chấm: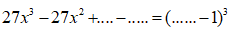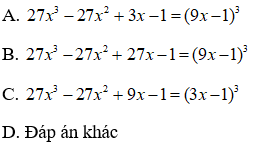Lời giải: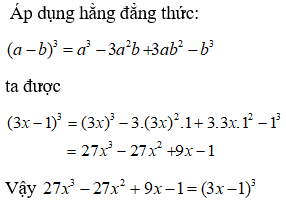Chọn đáp án C.Bài 8: Rút gọn biểu thức: A = (x – 2y).(x² + 2xy + y²) - (x + 2y). (x² – 2xy + y²)A. 2x³B. -16y³C. 16y³D. –2x³Lời giải:Áp dụng hằng đẳng thức:a³ – b³ = (a – b).(a² + ab + b²) và a³ + b³ = (a + b).(a² – ab + b²) ta được:A = (x – 2y). (x² + 2xy + y²) - (x + 2y). (x² – 2xy + y²)A = x³ – (2y)³ - [x³ + (2y)³]A = x³ – 8y³ – x³ – 8y³ = -16y³Chọn đáp án BBài 9: Tìm x biết x² – 16 + x(x – 4) = 0A. x = 2 hoặc x = - 4.B. x = 2 hoặc x = 4.C. x = -2 hoặc x = - 4.D. x = -2 hoặc x = 4.Lời giải:Ta có: x² – 16 + x(x – 4) = 0⇔ (x + 4). (x - 4) + x.(x – 4) = 0⇔ (x + 4 + x).(x - 4) = 0⇔ (2x + 4). (x - 4) = 0⇔ 2x + 4 = 0 hoặc x – 4 = 0* Nếu 2x + 4 = 0 thì x = -2* Nếu x – 4 =0 thì x = 4Vậy x = -2 hoặc x = 4.Chọn đáp án DBài 10: Rút gọn biểu thức A = (x + 2y ).(x - 2y) - (x – 2y)²A. 2x² + 4xyB. – 8y² + 4xyC. - 8y²D. – 6y² + 2xyLời giải:Ta có: A = (x + 2y ). (x - 2y) - (x – 2y)²A = x² – (2y)² – [x² – 2.x.2y +(2y)² ]A = x² – 4y² – x² + 4xy - 4y²2A = -8y² + 4xyChọn đáp án BBài 11: Chọn câu đúngA. (c + d)² – (a + b)² = (c + d + a + b)(c + d – a + b)B. (c – d)² – (a + b)² = (c – d + a + b)(c – d – a + b)C. (a + b + c – d)(a + b – c + d) = (a + b)² – (c – d)²D. (c – d)² – (a – b)² = (c – d + a – b)(c – d – a – b)Lời giải:Ta có:(c + d)² – (a + b)² = (c + d + a + b)(c + d – (a + b)) = (c + d + a + b)(c + d – a – b) nên A sai(c – d)² – (a + b)² = (c – d + a + b)[c – d – (a + b)] = (c – d + a + b)(c – d – a – b) nên B sai(c – d)² – (a – b)² = (c – d + a – b)(c – d – (a – b)) = (c – d + a – b)(c – d – a + b) nên D sai(a + b + c – d)(a + b – c + d) = [(a + b) + (c – d)][(a + b) – (c – d)] = (a + b)² – (c – d)² nên C đúngĐáp án cần chọn là: CBài 12: Chọn câu đúngA. 4 – (a + b)² = (2 + a + b)(2 – a + b)B. 4 – (a + b)² = (4 + a + b)(4 – a – b)C. 4 – (a + b)² = (2 + a – b)(2 – a + b)D. 4 – (a + b)² = (2 + a + b)(2 – a – b)Lời giải:Ta có 4 – (a + b)² = 2² – (a + b)² = (2 + a + b)[2 – (a + b)]                                                = (2 + a + b)(2 – a – b)Đáp án cần chọn là: DBài 13: Rút gọn biểu thức A = (3x – 1)² – 9x(x + 1) ta được:A. -15x + 1 B. 1            C. 15x + 1            D. – 1Lời giải:Ta có A = (3x – 1)² – 9x(x + 1)          = (3x)² – 2.3x.1 + 1 – (9x.x + 9x)          = 9x² – 6x + 1 – 9x² – 9x          = -15x + 1Đáp án cần chọn là: ABài 14: Rút gọn biểu thức A = 5(x + 4)² + 4(x – 5)² – 9(4 + x)(x – 4), ta được 2 ^{+ 4(x – 5)}2 ^{– 9(}A. 342        B. 243        C. 324        D. -324Lời giải:Ta có A = 5(x + 4)² + 4(x – 5)² – 9(4 + x)(x – 4)          = 5(x² + 2.x.4 + 16) + 4(x² – 2.x.5 + 5²) – 9(x² – 4²)          = 5(x² + 8x + 16) + 4(x² – 10x + 25) – 9(x² – 4²)          = 5x² + 40x + 80 + 4x² – 40x + 100 – 9x² + 144          = (5x² + 4x² – 9x²) + (40x – 40x) + (80 +100 + 144)          = 324Đáp án cần chọn là: CBài 15: Rút gọn biểu thức B = (2a – 3)(a + 1) – (a – 4)² – a(a + 7) ta đượcA. 0            B. 1            C. 19          D. – 19Lời giải:Ta có B = (2a – 3)(a + 1) – (a – 4)² – a(a + 7)          = 2a² + 2a – 3a – 3 – (a² – 8a + 16) – (a² + 7a)          = 2a² + 2a – 3a – 3 – a² + 8a – 16 – a² – 7a          = - 19Đáp án cần chọn là: DBài 16: Cho B = (x² + 3)² – x²(x² + 3) – 3(x + 1)(x – 1). Chọn câu đúng.A. B < 12   B. B > 13   C. 12 < B< 14D. 11 < B < 13Lời giải:Ta có B = (x² + 3)² – x²(x² + 3) – 3(x + 1)(x – 1).          = (x²)² +2.x².4 + 3² – (x².x² + x².3) – 3(x² – 1)                 = x⁴ + 6x² + 9 – x⁴ – 3x² – 3x² + 3 = 12Đáp án cần chọn là: DBài 17: Cho 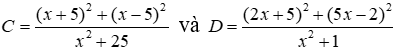. Tìm mối quan hệ giữa C và D.A. D = 14C + 1B. D = 14C C. D = 14C – 1D. D = 14C – 2Lời giải:Ta có: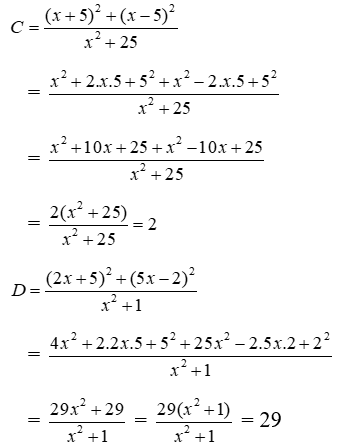Vậy D = 29; C = 2 suy ra D = 14C + 1 (do 29 = 14.2 + 1)Đáp án cần chọn là: ABài 18: Cho M = 4(x + 1)² +  (2x + 1)² – 8(x – 1)(x + 1) – 12x và N = 2(x – 1)² – 4(3 + x)² + 2x(x + 14).Tìm mối quan hệ giữa M và NA. 2N – M = 60B. 2M – N = 60C. M> 0, N < 0D. M > 0, N > 0Lời giải:Ta có:M = 4(x + 1)² +  (2x + 1)² – 8(x – 1)(x + 1) – 12= 4(x² + 2x + 1) + (4x² + 4x + 1) – 8(x² – 1) – 12x= 4x² + 8x + 4 + 4x² + 4x + 1 – 8x² +8 – 12x= (4x² + 4x² – 8x²) + (8x + 4x – 12x) + 4 + 1 +8= 13N = 2(x – 1)² – 4(3 + x)² + 2x(x + 14)= 2(x² – 2x + 1) – 4(9 + 6x + x²) + 2x² + 28x= 2x² – 4x + 2 – 36 – 24x – 4x² + 2x² + 28x= (2x² +2x² – 4x²) + (-4x – 24x + 28x) + 2 – 36= -34Suy ra M = 13, N = -34 ⇔ 2M – N = 60Đáp án cần chọn là: BBài 19: Có bao nhiêu giá trị x thỏa mãn (2x – 1)² – (5x – 5)² = 0A. 0            B. 1            C. 2            D. 3Lời giải: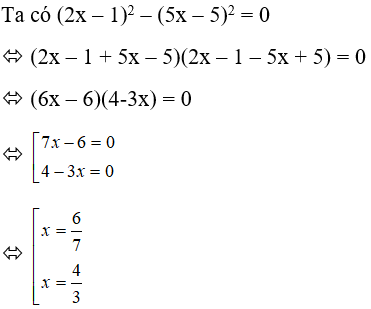Vậy có hai giá trị của x thỏa mãn yêu cầuĐáp án cần chọn là: CBài 20: Có bao nhiêu giá trị x thỏa mãn (2x + 1)² – 4(x + 3)² = 0A. 0            B. 1            C. 2            D. 3Lời giải:Ta có: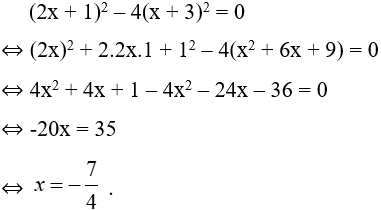Vậy có một giá trị của x thỏa mãn yêu cầu.Đáp án cần chọn là: BII. Bài tập tự luậnBài 1: Cho đa thức 2x² – 5x + 3. Viết đa thức trên dưới dạng 1 đa thức của biến y trong đó y=x+1.Lời giải:Theo đề bài ta có: y = x + 1 => x = y – 1.A = 2x² – 5x + 3= 2(y – 1)² – 5(y – 1) + 3 = 2(y² – 2y + 1) – 5y + 5 + 3 = 2y² – 9y + 10Bài 2: So sánh hai số sau, số nào lớn hơn?a) A = (2 + 1)(2²+ 1)(2⁴+ 1)(2⁸ + 1)(2¹⁶ + 1) và B = 2³²b) A = 1989.1991 và B = 1990²_{Lời giải:}a) Ta nhân 2 vế của A với 2 – 1, ta được:A = (2 – 1)(2 + 1)(2² + 1)(2⁴ + 1)(2⁸ + 1)(2¹⁶ + 1)Ta áp dụng đẳng thức ( a- b)(a + b) = a² – b² nhiều lần, ta được:A = 2³² – 1.=> Vậy A < B.b) Ta đặt 1990 = x => B = x²Vậy A = (x – 1)(x + 1) = x² – 1=> B > A là 1.Bài 3: Tìm giá trị nhỏ nhất của các biểu thức sau:a) A = x² – 4x + 1b) B = 4x² + 4x + 11c) C = 3x² – 6x – 1Lời giải:a) Ta sẽ biến đổi A= x² – 4x + 1 = x² – 4x + 4 – 3 = ( x- 2)² – 3Do ( x- 2)² > 0 nên => ( x- 2)² – 3 ≥ -3Vậy giá trị nhỏ nhất của biểu thức A(A_{min) = -3 khi và chỉ khi x = 2.}b) B = 4x² + 4x + 11 = (2x + 1)² + 10Vậy B_min = 10 khi và chỉ khi x = -$\frac{1}{2}$.c) C = 3x² – 6x – 1 = 3(x – 1)² – 4Vậy C_min = -4 khi và chỉ khi x = 1.Bài 4: Cho a + b + c = 2p. Chứng minh rằng: 2bc + b² + c² – a² = 4p(p – a)Lời giải:Ta sẽ đi biến đổi VP.VP = 2p(2p – 2a) = (a + b + c)( a + b – c) = ( b + c )² – a² = b² + 2bc + c² – a² = VT (đccm)Bài 5: Hiệu các bình phương của 2 số tự nhiên chẵn liên tiếp bằng 36. Tìm hai số ấy.Lời giải:Gọi 2 số chẵn liên tiếp là x và x + 2 (x chẵn). Ta có:(x + 2)² – x² = 36<=> x² + 4x + 4 – x² = 36<=> 4x = 32<=> x = 8=> số thứ 2 là 8+2 = 10Đáp số: 8 và 10Bài 6: Viết các biểu thức sau dưới dạng bình phương một tổng:a, x² + 6x + 9b, x² + x + 1/4c,2xy² + x²y⁴ + 1Lời giải:a, x² + 6x + 9 = x² + 2.x.3 + 3² = (x + 3)²b, x² + x + 1/4 = x² + 2.x.1/2 + (1/2 )² = (x + 1/2)²c, 2xy² + x²y⁴ + 1 = (xy²)² + 2.xy².1 + 1² = (xy² + 1)²Bài 7: Rút gọn biểu thức:a, (x + y)² + (x – y)²b, 2(x – y)(x + y) + (x + y)² + (x – y)²c, (x – y + z)² + (z – y)² + 2(x – y + z)(y – z)Lời giải:a, (x + y)² + (x – y)²= x² + 2xy + y² + x² – 2xy + y²= 2x² + 2y²b, 2(x – y)(x + y) + (x + y)² + (x – y)²= [(x + y) + (x – y)]² = (2x)² = 4x²c, (x – y + z)² + (z – y)² + 2(x – y + z)(y – z)= (x – y + z)² + 2(x – y + z)(y – z) + (y – z)²= [(x – y + z) + (y – z)]² = x²Bài 8: Tính giá trị của biểu thức sau:a, x² – y² tại x = 87 và y = 13b, x³ – 3x² + 3x – 1 tại x = 101c, x³ + 9x²+ 27x + 27 tại x = 97Lời giải:a, Ta có: x² – y² = (x + y)(x – y)b, Thay x = 87, y = 13, ta được:x² – y² = (x + y)(x – y)= (87 + 13)(87 – 13)= 100.74 = 7400c, Ta có: x³ + 9x² + 27x + 27= x³ + 3.x².3 + 3.x.3² + 3³= (x + 3)³Thay x = 97, ta được: (x + 3)³ = (97 + 3)³ = 100³ = 1000000Bài 9: Chứng minh rằng:a, (a + b)(a² – ab + b²) + (a – b)(a² + ab + b²) = 2a³b, (a + b)[(a – b)² + ab] = (a + b)[a² – 2ab + b² + ab] = a³ + b³Lời giải:a, Ta có: (a + b)(a² – ab + b²) + (a – b)(a² + ab + b²) = a³ + b³ + a³ – b³ = 2a³Vế trái bằng vế phải nên đẳng thức được chứng minh.b, Ta có: (a + b)[(a – b)² + ab] = (a + b)[a² – 2ab + b² + ab]= (a + b)(a² – 2ab + b²) = a³ + b³Vế phải bằng vế trái nên đẳng thức được chứng minh.Bài 10: Chứng tỏ rằng:a, x² – 6x + 10 > 0 với mọi xb, 4x – x² – 5 < 0 với mọi xLời giải:a, Ta có: x² – 6x + 10 = x² – 2.x.3 + 9 + 1 = (x – 3)² + 1Vì (x – 3)² ≥ 0 với mọi x nên (x – 3)² + 1 > 0 mọi xVậy x² – 6x + 10 > 0 với mọi x.b, Ta có: 4x – x2 – 5 = -(x² – 4x + 4) – 1 = -(x – 2)² -1Vì (x – 2)² ≥ 0 với mọi x nên –(x – 2)² ≤ 0 với mọi x.Suy ra: -(x – 2)² -1 ≤ 0 với mọi xVậy 4x – x2 – 5 < 0 với mọi x.III. Bài tập vận dụngBài 1: Tính.Bài 2: Rút gọn rồi tính giá trị biểu thức.Bài 3: viết biểu thức  thành tích chứng minh với moi số nguyên n biểu thức  chia hết cho 8.Bài 4: Chứng minh với moi số nguyên N biểu thức  chia hết cho 4.Bài 5: Viết biểu thức sau dưới dang tích:Bài 6: Chứng minh các hằng đẳng thức sau:a) (a² – b²)² + (2ab)² = (a² + b²)²b) (a² + b²)(c² + d²) = (ac + bd)² + (ad – bc)²Bài 7: Tìm giá trị lớn nhất của các biểu thức sau:a) 5 – 8x – x²b) 4x – x² + 1Bài 8: Tổng 3 số a, b, c bằng 9, Tổng các bình phương của chúng bằng 53. Tính ab + bc + ca.Bài 9: Cho a + b + c = 2p. Chứng minh rằng:(p – a)² + (p – b)² + (p – c)² = a² + b² + c² – p²Bài 10: Tính giá trị của các biểu thức:a) x² – 10x + 26 với x = 105b) x² + 0,2x + 0,01 với x = 0,9