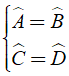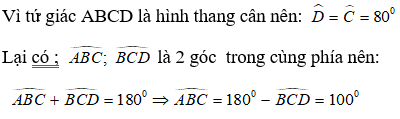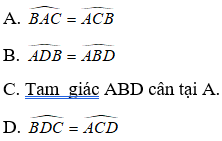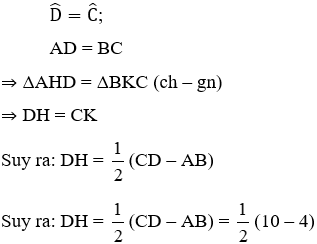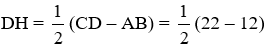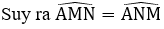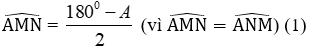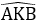50 Bài tập Hình thang cân Toán 8 mới nhất

Bài tập Hình thang cân - Toán 8

I. Bài tập trắc nghiệm

Bài 1: Điền cụm từ thích hợp vào chỗ trống

A. Hình thang cân là…………………………………..

B. Hình thang có………………. là hình thang cân .

C. Hai cạnh bên của hình thang cân…………………..

D. Hình thang cân có hai góc kề một đáy…………….

Lời giải:

+ Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.

→ Đáp án A điền: “hình thang có hai góc kề một đáy bằng nhau”.

+ Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.

→ Đáp án B điền: “hai góc kề một đáy bằng nhau”

+ Hai cạnh bên của hình thang cân bằng nhau.

→ Đáp án C điền: “bằng nhau”

+ Hình thang cân là hình thang có hai góc kề một đáy bằng nhau

→ Đáp án D điền: “bằng nhau”

Bài 2: Điền chữ “Đ” hoặc “S” vào mỗi câu khẳng định sau:

A. Tứ giác có hai cạnh bên bằng nhau là hình thang cân.

B. Hình thang cân có hai cạnh bên bằng nhau.

C. Hình thang cân có hai góc kề một cạnh đáy bù nhau.

D. Hình thang cân có hai góc kề một cạnh đáy bằng nhau.

Lời giải:

+ Tứ giác có hai cạnh bên bằng nhau là hình thang cân.

→ Đáp án A sai vì hai cạnh bên bằng nhau chưa chắc tạo ra hình thang.

+ Hình thang cân có hai cạnh bên bằng nhau.

→ Đáp án B đúng.

+ Hình thang cân có hai góc kề một cạnh đáy bằng nhau.

→ Đáp án D đúng, đáp án C sai.

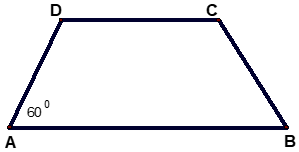
Bài 3: Cho hình thang cân ABCD (như hình vẽ) có $\widehat{BAD}$ = 60⁰. Số đo của $\widehat{BCD}$ˆ = ?

A. 50⁰   

B. 60⁰

C. 120⁰   

D. 80⁰

Lời giải:

Áp dụng tính chất của hình thang cân ta có:

Mà $\hat{A}+\hat{B}+\hat{C}+\hat{D}$ˆ = 360⁰ ⇔ $2\hat{A}+2\hat{C}$ = 360⁰

⇒ 2$\hat{C}$= 360⁰ - 2$\hat{A}$ˆ = 360⁰ - 2.60⁰ = 240⁰ ⇔ Cˆ = 120⁰

Chọn đáp án C.

Bài 4: Cho hình thang cân ABCD (AB // CD) . Tìm mệnh đề sai?

Lời giải:

Chọn đáp án D

Bài 5: Cho hình thang cân ABCD (AB// CD) và $\hat{D}$ˆ = 80^o. Tính $\widehat{ABC}$ˆ

A. 100^o    

B. 90^o

C. 80^o    

D. 110^o

Lời giải:

Chọn đáp án A

Bài 6: Cho hình thang ABCD có AB // CD , hai đường chéo AC và BD cắt nhau tại O sao cho OA = OB; OC = OD . Tìm khẳng định sai trong các khẳng định sau?

A. ABCD là hình thang cân

B. AC = BD

C. BC = AD

D. Tam giác AOD cân tại O.

Lời giải:

* Ta có: OA = OB nên tam giác OAB cân tại O

* Do OC = OD nên tam giác OCD cân tại O

* vì OA = OB và OC = OD nên OA + OC = OB + OD

Hay AC = BD

Hình thang ABCD có hai đường chéo AC = BD nên đây là hình thang cân.

Suy ra: BC = AD và $\widehat{BAD}=\widehat{ABC}$ˆ; $\widehat{ADC}=\widehat{DCB}$ˆ

Chọn đáp án D

Bài 7: Cho hình thang cân ABCD có AB // CD và $\hat{A}$ˆ = 125^o. Tính $\hat{B}$?

A. 125^o    

B. 65^o

C. 90^o    

D. 55^o

Lời giải:

Theo định nghĩa hình thang cân ta có: $\hat{A}=\hat{B}$ = 125^o

Chọn đáp án A

Bài 8: Cho hình thang cân ABCD có AB// CD và AB = BC. Tìm khẳng định sai.

Lời giải:

* Xét tam giác ABC có AB = BC nên tam giác ABC cân tại B.

Suy ra: $\widehat{BAC}=\widehat{ACB}$ˆ

* Vì ABCD là hình thang cân nên AD = BC

Lại có AB = BC nên AB = AD.

* Suy ra: ΔABD cân tại A nên $\widehat{ADB}=\widehat{ABD}$ˆ

Chọn đáp án D

Bài 9: Cho hình thang cân ABCD có AB // CD. Gọi giao điểm của AD và BC là M . Tam giác MCD là tam giác gì ?

A. Tam giác cân    

B. Tam giác nhọn

C. Tam giác vuông    

D. Tam giác tù

Lời giải:

ABCD là hình thang cân nên: $\hat{D}=\hat{C}$ˆ

Xét tam giác MCD có $\hat{D}=\hat{C}$ˆ nên đây là tam giác cân tại M

Chọn đáp án A

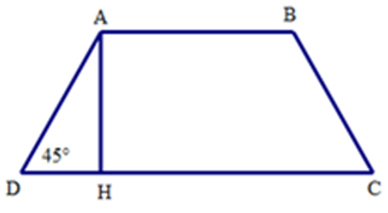
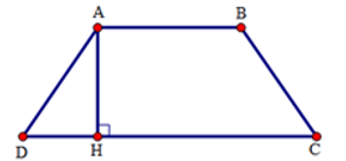
Bài 10: Cho hình thang cân ABCD có đáy nhỏ AB = 3cm, đường AH = 5cm, và  = 45⁰. Độ dài đáy lớn CD bằng

A. 13 cm        

B. 10 cm         

C. 12 cm         

D. 8 cm

Lời giải:

Ta có tam giác ADH vuông cân tại H vì 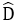 = 45⁰.

Do đó DH = AH = 5cm

Mà DH = 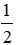(CD – AB)

Suy ra CD = 2DH + AB = 2.5 + 3 = 13 (cm)

Vậy CD = 13 cm

Đáp án cần chọn là: A

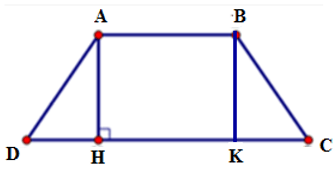
Bài 11: Cho hình thang cân ABCD đáy nhỏ AB = 4cm, đáy lớn CD = 10cm, cạnh bên BC = 5cm thì đường cao AH bằng:

A. 4,5 cm       

B. 4 cm           

C. 3,5 cm        

D. 3 cm

Lời giải:

Kẻ BK ⊥ DC tại K.

Vì ABCD là hình thang cân nên ta có:

Do ABCD là hình thang cân nên AD = BC = 5 cm

Áp dụng định lí Py-ta-go vào tam giác ADH vuông tại H ta có

AD² = AH² + DH²

⇒ AH² = AD² – DH² = 5² – 3²

⇒ AH = 4

Vậy AH = 4cm

Đáp án cần chọn là: B

Bài 12: Cho hình thang cân ABCD đáy nhỏ AB = 12cm, đáy lớn CD = 22cm, cạnh bên BC = 13cm thì đường cao AH bằng:

A. 9 cm          

B. 8 cm           

C. 12 cm         

D. 6 cm

Lời giải:

Ta có: 

Do ABCD là hình thang cân nên AD = BC = 13 cm

Áp dụng định lí Py-ta-go vào tam giác ADH vuông tại H ta có

AD² = AH² + DH²

⇒ AH² = AD² – DH² = 13² – 5²

⇒ AH = 12

Vậy AH = 12cm

Đáp án cần chọn là: C

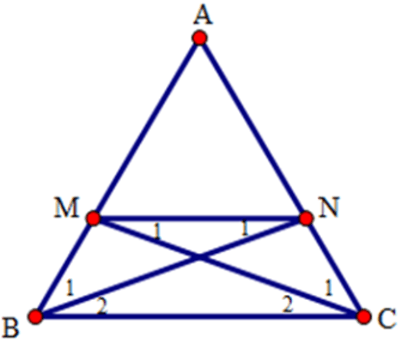
Bài 13: Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy các điểm M, N sao cho BM = CN. Tứ giác BMNC là hình gì?

A. Hình thang            

B. Hình thang cân      

C. Hình thang vuông  

D. Cả A, B, C đều sai

Lời giải:

Ta có AB = AM + MB và AC = AN + NC

Mà AB = AC (do tam giác ABC cân tại A) và BM = NC (gt)

Suy ra AN = AM

Xét tam giác AMN cân tại A.

Xét tam giác ANM có: 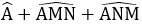 (tổng ba góc trong một tam giác)

Xét tam giác ABC cân tại A ta có:

(tổng ba góc trong một tam giác) nên  (2)

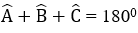
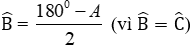
Từ (1) và (2) suy ra: 

Mà  là hai góc đồng vị nên MN // BC

Xét tứ giác MNCB có MN // BC nên MNCB là hình thang.

Lại có 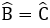 (do ΔABC cân tại A) nên MNCB là hình thang cân.

Đáp án cần chọn là: B

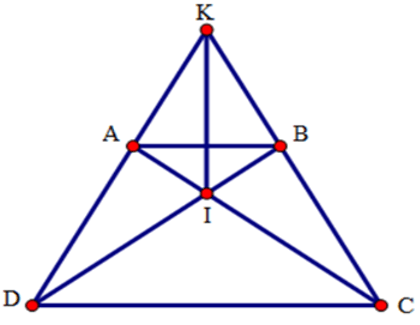
Bài 14: Cho hình thang cân ABCD (AB // CD) có hai đường chéo cắt nhau tại I, hai đường thẳng AD và BC cắt nhau ở K. Chọn khẳng định đúng:

A. KI là đường trung trực của hai đáy AB và CD

B. KI là đường trung trực của đáy AB nhưng không là đường trung trực của CD

C. KI là đường trung trực của đáy CD nhưng không là trung trực của AB

D. KI không là đường trung trực của cả hai đáy AB và CD.

Lời giải:

Xét tam giác ACD và tam giác BDC có:

+ AD = BC (do ABCD là hình thang cân)

+ AC = BD (do ABCD là hình thang cân)

+ CD là cạnh chung

Suy ra ΔACD = ΔBDC (c.c.c)

Suy ra 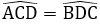 (cmt), suy ra tam giác ICD cân tại I. Do đó ID = IC (1)

Tam giác KCD có hai góc ở đáy bằng nhau nên tam giác KCD cân ở K.

Do đó KC = KD (2)

Từ (1) và (2) suy ra KI là đường trung trực của CD (*).

Xét tam giác ADB và tam giác BCA có:

+ AD = BC (cmt)

+ AB là cạnh chung

+ AC = BD

Suy ra ΔADB = ΔBCA (c.c.c)

Suy ra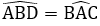  

Xét tam giác IAB có 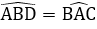 nên tam giác IAB cân tại I.

Do đó IA = IB (3)

Ta có KA = KD – AD; KB = KC – BC

Mà KD = KC, AD = BC, do đó KA = KB (4)

Từ (3) và (4) suy ra KI là đường trung trực của AB. (**)

Từ (*) và (**) suy ra KI là đường trung trực của hai đáy (đpcm)

Đáp án cần chọn là: A

Bài 15: Cho hình thang cân ABCD (AB // CD) có hai đường chéo cắt nhau tại I, hai đường thẳng AD và BC cắt nhau ở K. Chọn câu sai.

A. ΔKAB cân tại K                

B. ΔKCD cân tại K

C. ΔICD đều                          

D. KI là đường phân giác 

Lời giải:

Xét tam giác ACD và tam giác BDC có:

+ AD = BC (do ABCD là hình thang cân)

+ AC = BD (do ABCD là hình thang cân)

+ CD là cạnh chung

Suy ra ΔACD = ΔBDC (c.c.c)

Suy ra 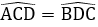 (hai góc tương ứng), suy ra tam giác ICD cân tại I.

Nên C sai vì ta chưa đủ điều kiện để IC = CD

Tam giác KCD có hai góc ở đáy bằng nhau nên tam giác KCD cân ở K nên B đúng.

Xét tam giác KDI và tam giác KCI có:

+ KD = KC (do ΔKCD cân tại K))

+ KI là cạnh chung

+ IC = ID

Suy ra ΔKDI = ΔKCI (c.c.c)

Suy ra 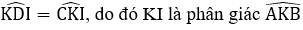 nên D đúng.

Ta có AB // CD (do ABCD là hình thang) nên 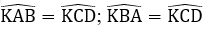 (các cặp góc đồng vị bằng nhau)

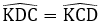
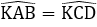
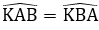
Mà  (tính chất hình thang cân) nên   (tính chất hình thang cân) nên  hay ΔKAB cân tại K. Do đó A đúng

Đáp án cần chọn là: C

II. Bài tập tự luận có lời giải

Bài 1: Hình thang cân ABCD có AB //CD, AB < CD. Kẻ các đường cao AH, BK. Chứng minh rằng: DC = CK

Lời giải:

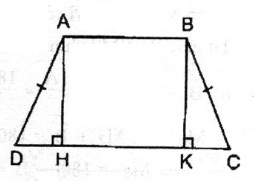
Xét hai tam giác vuông AHD và BKC:

$\widehat{AHD}=\widehat{BKC}$ = 90^o

AD = BC (tính chất hình thang cân)

$\hat{C}=\hat{D}$ (gt)

Suy ra: ΔAHD = ΔBKC (cạnh huyền, góc nhọn)

⇒ HD = KC

Bài 2 Hình thang cân ABCD có AB // CD, O là giao điểm của hai đường chéo. Chứng minh rằng OA = OB, OC = OD.

Lời giải:

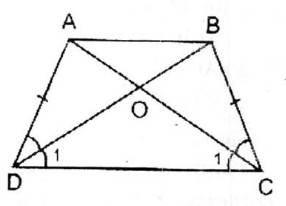
Xét ΔADC và ΔBCD, ta có:

AD = BC (tính chất hình thang cân)

$\widehat{ACD}=\widehat{BCD}$ (gt)

DC chung

Do đó: ΔADC = ΔBCD (c.g.c) ⇒ $\widehat{C_1}=\widehat{D_1}$

Trong ΔOCD ta có: $\widehat{C_1}=\widehat{D_1}$ ⇒ ΔOCD cân tại O ⇒ OC = OD (1)

AC = BD (tính chất hình thang cân) ⇒ AO + OC = BO + OD (2)

Từ (1) và (2) suy ra: AO = BO.

Bài 3 Cho tam giác ABC cân tại A. Trên cạnh AB, AC lấy các điểm M, N sao cho BM = CN

a, Tứ giác BMNC là hình gì? Vì sao?

b, Tính các góc của tứ giác BMNC biết rằng góc $\hat{A}$ = 40^o

Lời giải:

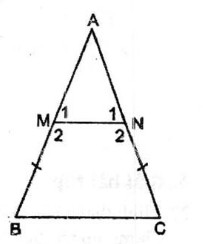
a, ΔABC cân tại A

⇒$\hat{B}=\hat{C}$ = $\frac{({180}^o-\hat{A} )}{2}$ (tính chất tam giác cân) (1)

AB = AC (gt) ⇒ AM + BM = AN + CN

Mà BM = CN (gt) ⇒ AM = AN

⇒ ΔAMN cân tại A

⇒$\widehat{M_1}=\widehat{N_1}$ = $\frac{({180}^0-\hat{A})}{2}$ (tính chất tam giác cân) (2)

Từ (1) và (2) suy ra: $\widehat{M_1}=\hat{B}$

⇒ MN // BC (vì có cặp góc đồng vị bằng nhau)

Tứ giác BCNM là hình thang có B = C

Vậy BCNM là hình thang cân.

b, $\hat{B}=\hat{C}=\frac{({180}^o – {40}^o)}{2}$ = 70^o

Mà $\widehat{M_2}+\hat{B}$ = 180^o – 70^o = 110^o

$\widehat{N_2}=\widehat{M_2}$= 110^o (tính chất hình thang cân)

Bài 4 Cho tam giác ABC cân tại A, các đường phân giác BE, CF. Chứng minh rằng BFEC là hình thang cân có đáy nhỏ bằng cạnh bên.

Lời giải:

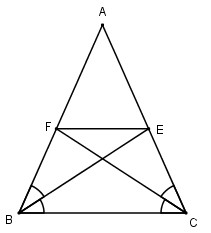
Xét hai tam giác AEB và AFC

Có AB = AC (ΔABC cân tại A)

$\widehat{ABE}=\frac{\hat{B}}{2}=\frac{\hat{C}}{2}=\widehat{ACF}$

$\hat{A}$ là góc chung

⇒ ΔAEB = ΔAFC (g.c.g) ⇒ AE = AF ⇒ ΔAEF cân tại A

⇒ $\widehat{AFE}$ = $\frac{{180}^0-\hat{A}}{2}$ và trong tam giác ΔABC: $\hat{B}=\frac{\left({180}^0-\hat{A}\right)}{2}$

⇒$\widehat{AFE}=\hat{B}$ ⇒ FE//BC

⇒ Tứ giác BFEC là hình thang.

Vì FE//BC nên ta có: $\widehat{FEB}=\widehat{EBC}$ (so le trong)

Lại có: $\widehat{FBE}=\widehat{EBC}$

⇒$\widehat{FBE}=\widehat{FEB}$

⇒ ΔFBE cân ở F ⇒ FB = FE

⇒ Hình thang BFEC là hình thang cân có đáy nhỏ bằng cạnh bên (đpcm)

Bài 5 Chứng minh hình thang có hai đường chéo bằng nhau là hình thang cân.

Lời giải:

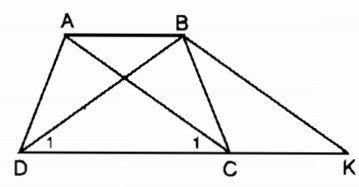
Từ B kẻ đường thẳng song song với AC cắt đường thẳng DC tại K.

Ta có hình thang ABKC có hai cạnh bên BK // AC nên AC = BK

Mà AC = BD (gt)

Suy ra: BD = BK do đó ΔBDK cân tại B

⇒ $\widehat{D_1}=\hat{K}$ (tính chất hai tam giác cân)

Ta lại có: $\widehat{C_1}=\hat{K}$ (hai góc đồng vị)

Suy ra: $\widehat{D_1}=\widehat{C_1}$

Xét ΔACD và ΔBDC:

AC = BD (gt)

$\widehat{D_1}=\widehat{C_1}$ (chứng minh trên)

CD chung

Do đó ΔACD = ΔBDC (c.g.c) ⇒ $\widehat{ADC}=\widehat{BCD}$

Hình thang ABCD có $\widehat{ADC}=\widehat{BCD}$ nên là hình thang cân.

Bài 6 Tính các góc của hình thang cân, biết một góc bang 50^o

Lời giải:

Giả sử hình thang ABCD có AB // CD và $\hat{D}$ = 50^o

Vì $\hat{C}=\hat{D}$ (tính chất hình thang cân)

⇒ $\hat{C}$ = 50^o

$\hat{A}+\hat{D}$ = 180^o (hai góc trong cùng phía)

⇒ $\hat{A}$ = 180^o - $\hat{D}$ = 180^o – 50^o = 130^o

$\hat{B}=\hat{A}$ (tính chất hình thang cân)

Suy ra: $\hat{B}$ = 130^o

Bài 7 Hình thang cân ABCD có đáy nhỏ AB bằng cạnh bên AD. Chứng minh rằng CA là tia phân giác của góc C.

Lời giải:

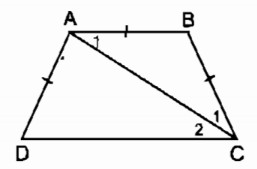
Ta có:

AB = AD (gt)

AD = BC (tính chất hình thang cân)

⇒ AB = BC do đó $∆$ABC cân tại B

⇒ $\hat{A}=\hat{C}$ (tính chất tam giác cân)

Mặt khác: AB//CD (gt)

$\widehat{A_1}=\widehat{C_2}$ (hai góc so le trong)

Suy ra: $\widehat{C_1}=\widehat{C_2}$

Vậy CA là tia phân giác của (BCD)

Bài 8 Hai đoạn thẳng AB và CD cắt nhau tại 0. Biết rằng OA = OC, OB = OD. Tứ giác ABCD là hình gì ? Vì sao

Lời giải:

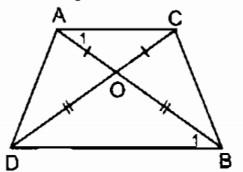
Ta có: OA = OC (gt)

⇒ ΔOAC cân tại O

⇒$\widehat{A_1}=\frac{{180}^0-\widehat{AOC}}{2}$ (tính chất tam giác cân) (1)

OB = OD (gt)

⇒ ΔOBD cân tại O

⇒ $\widehat{B1}=\frac{{180}^0-\widehat{BOD}}{2}$ (tính chất tam giác cân) (2)

$\widehat{AOC}=\widehat{BOD}$ (đối đỉnh) (3)

Từ (1), (2), (3) suy ra: $\widehat{A_1}=\widehat{B_1}$

⇒ AC // BD (vì có cặp góc ở vị tri so le trong bằng nhau)

Suy ra: Tứ giác ABCD là hình thang

Ta có: AB = OA + OB

CD = OC + OD

Mà OA = OC, OB = OD

Suy ra: AB = CD

Vậy hình thang ABCD là hình thang cân.

Bài 9 Cho tam giác ABC cân tại A. Lấy điểm D trên cạnh AB, điểm E trên cạnh AC sao cho AD = AE

a, Tứ giác BDEC là hình gì? Vì sao

b, Các điểm D, E ở vị trí nào thì BD =DE = EC?

Lời giải:

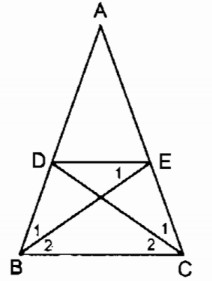
a, AD = AE (gt)

⇒ ΔADE cân tại A ⇒$\widehat{ADE}=\frac{({180}^0-\hat{A})}{2}$

ΔABC cân tại A ⇒ $\widehat{ABC}=\frac{{180}^0-\hat{A}}{2}$

Suy ra: $\widehat{ADE}=\widehat{ABC}$

⇒ DE // BC (Vì có cặp góc đồng vị bằng nhau)

Tứ giác BDEC là hình thang

$\widehat{ABC}=\widehat{ACB}$ (tính chất tam giác cân) hay $\widehat{DBC}=\widehat{ECB}$

Vậy BDEC là hình thang cân.

b, Ta có: BD = DE ⇒ ΔBDE cân tại D

$\widehat{B_1}=\widehat{E_1}$

Mà $\widehat{E_1}=\widehat{B_2}$ (so le trong)

⇒ $\widehat{B_1}=\widehat{B_2}$

DE = EC ⇒ ΔDEC cân tại E

⇒ $\widehat{D_1}=\widehat{C_1}$

$\widehat{D_1}=\widehat{C_2}$(so le trong)

⇒ $\widehat{C_1}=\widehat{C_2}$

Vậy khi BE là tia phân giác của $\widehat{ABC}$, CD là tia phân giác của $\widehat{ACB}$ thì BD = DE = EC.

Bài 10 Hình thang cân ABCD có 0 là giao điểm của hai đường thắng chứa cạnh bên AD, BC và E là giao điểm của hai đường chéo. Chứng minh rằng OE là đường trung trực của hai đáy.

Lời giải:

Ta có: $\widehat{ADC}=\widehat{BCD}$ (gt)

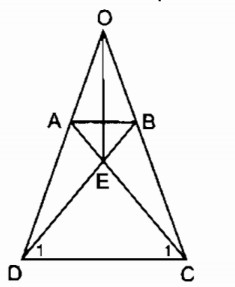
⇒ $\widehat{ODC}=\widehat{OCD}$

⇒ΔOCD cân tại O

⇒ OC = OD

OA + AD = OB + BC

Mà AD = BC (tính chất hình thang cân)

⇒ OA = OB

Xét ΔADC và. ΔBCD:

AD = BC (chứng minh trên)

AC = BD (tính chất hình thang cân)

CD chung

Do đó ΔADC và ΔBCD (c.c.c)

⇒ $\widehat{D_1}=\widehat{C_1}$

⇒ΔEDC cân tại E

⇒ EC = ED nên E thuộc đường trung trực CD

OC = OD nên O thuộc đường trung trực CD

E ≠ O. Vậy OE là đường trung trực của CD.

Ta có: BD= AC (chứng minh trên)

⇒ EB + ED = EA + EC mà ED = EC

⇒ EB = EA nên E thuộc đường trung trực AB

OA = OB nên O thuộc đường trung trực của AB

E ≠O. Vậy OE là đường trung trực của AB.

Bài 11

a, Hình thang ABCD có đáy nhỏ AB = b , đáy lớn CD = a, đường cao AH. Chứng minh rằng HA = $\frac{\left(a-b\right)}{2}$ , HC = $\frac{\left(a+b\right)}{2}$ (a, b có cùng đơn vị đo).

b, Tính đường cao của hình thang cân có hai đáy 10cm, 26cm và cạnh bên 17cm.

Lời giải:

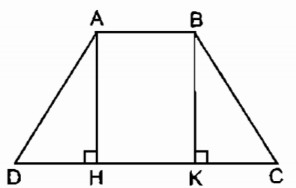
a, Kẻ đường cao BK

Xét hai tam giác vuông AHD và BKC, ta có:

$\widehat{AHD}=\widehat{BKC}$ = 90^o

AD = BC (tỉnh chất hình thang-Cân)

$\hat{D}=\hat{C}$(gt)

Do đó: ΔAHD = ΔBKC (cạnh huyền, góc nhọn) ⇒ HD = KC.

Hình thang ABKH có hai cạnh bên song song nên AB = HK

a – b = DC – AB = DC – HK = HD + KC = 2HD ⇒ HD = $\frac{\left(a-b\right)}{2}$

HC = DC – HD = $\frac{a-\left(a-b\right)}{2}=\frac{\left(a+b\right)}{2}$

b, HD = $\frac{\left(CD-AB\right)}{2}=\frac{\left(26-10\right)}{2}$ = 8 (cm)

Trong tam giác vuông AHD có $\widehat{AHD}$ = 90^o

AD² = AH² + HD² (định lý Pi-ta-go)

⇒ AH² = AD² - HD²

AH² = l7² - 8²= 289 – 64 = 225

AH = 15 (cm)

Bài 12 Hình thang cân ABCD có đường chéo BD vuông góc với cạnh bên BC, BD là tia phân giác của-góc D. Tính chu vi của hình thang, biết BC = 3cm.

Lời giải:

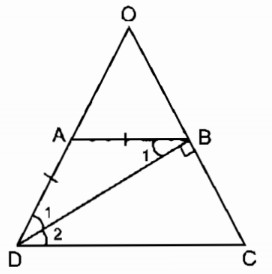
Ta có: AD = BC = 3 (cm) (tính chất hình thang cân)

$\widehat{ABD}=\widehat{BDC}$ (so le trong)

$\widehat{ADB}=\widehat{BDC}$ (gt)

⇒ $\widehat{ABD}=\widehat{ABD}$

⇒ΔABD cân tại A

⇒ AB = AD = 3 (cm)

ΔBDC vuông tại B

$\widehat{BDC}+\hat{C}$ = 90^o

$\widehat{ADC}=\hat{C}$ (gt)

Mà $\widehat{BDC}=\frac{1}{2}\widehat{ADC}$ = $\frac{1}{2}\widehat{ADC}$ nên $\widehat{BDC}=\frac{1}{2}\hat{C}$

$\hat{C}+\frac{1}{2}\hat{C}$ = 90^o ⇒ $\hat{C}$ = 60^o

Từ B kẻ đường thẳng song song AD cắt CD tại E.

Hình thang ABED có hai cạnh bên song song nên AB = DE và AD = BE

⇒ DE = 3 (cm), BE = 3 (cm)

$\widehat{BEC}=\widehat{ADC}$ (đồng vị)

Suy ra: $\widehat{BEC}=\hat{C}$

⇒ΔBEC cân tại B có $\hat{C}$ = 60^o

⇒ΔBEC đều

⇒ EC = BC = 3 (cm)

CD = CE + ED = 3 + 3 = 6(cm)

Chu vi hình thang ABCD bằng:

AB + BC + CD + DA = 3 + 3 + 6 + 3 = 15 (cm)

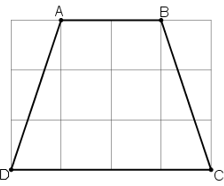
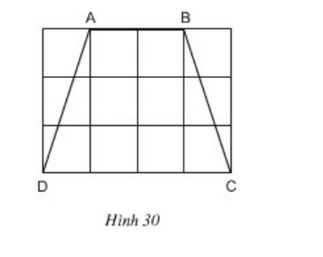
Bài 13 Tính độ dài các cạnh của hình thang cân ABCD trên giấy kẻ ô vuông (h.30, độ dài của cạnh ô vuông là 1cm)

Bài giải:

Vì độ dài của cạnh ô vuông là 1cm nên độ dài của cạnh:

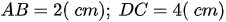
Áp dụng định lí Py ta go trong tam giác vuông EAD, ta có:

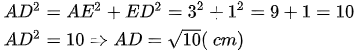
Vì tứ giác ABCD là hình thang cân nên :

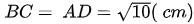
Vậy độ dài các cạnh của hình thang ABCD là:

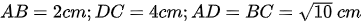
Bài 14 Cho hình thang cân ABCD. Kẻ các đường cao AE, BF của hình thang. Chứng minh rằng .

Bài giải:

Vì ABCD là hình thang cân nên ta có:

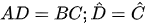
Xét hai tam giác vuông EAD và FBC ta có:

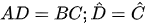
Vậy 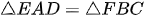 (ch-gn). Suy ra  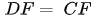(dpcm)

Bài 15 Cho hình thang cân ABCD , E là giao điểm của hai đường chéo. Chứng minh rằng .

Bài giải:

Do ABCD là hình thang cân nên: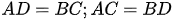 

Xét hai tam giác ADC và BCD, ta có:

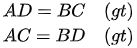
DC: cạnh chung

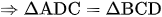 (c.c.c)  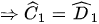(hai góc tương ứng)

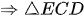 cân tại E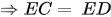 

Mà 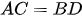 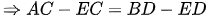 hay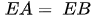 

Vậy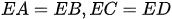 

III. Bài tập vận dụng

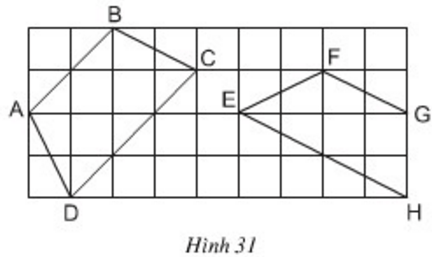
Bài 1 Cho các tứ giác ABCD và EFGH trên giấy kẻ ô vuông (h.31), tứ giác nào là hình thang cân ?

Vì sao ?

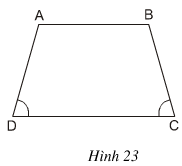
Bài 2 Hình thang ABCD (AB // CD) trên hình 23 có gì đặc biệt?

Bài 3 Cho hình 24.

a) Tìm các hình thang cân.

b) Tính các góc còn lại của mỗi hình thang cân đó.

c) Có nhận xét gì về hai góc đối của hình thang cân?

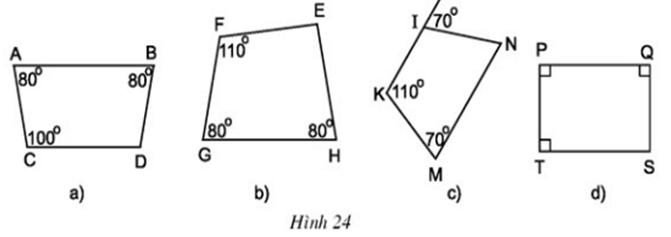
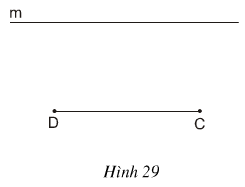
Bài 4 Cho đoạn thẳng CD và đường thẳng m song song với CD (h.29). Hãy vẽ các điểm A, B thuộc m sao cho ABCD là hình thang có hai đường chéo CA, DB bằng nhau. Sau đó hãy đo các góc C và D của hình thang ABCD đó để dự đoán về dạng của các hình thang có đường chéo bằng nhau.

Bài 5 Tính độ dài các cạnh của hình thang cân ABCD trên giấy kẻ ô vuông (h.30, độ dài của cạnh ô vuông là 1cm).

Bài 6 Cho hình thang cân ABCD (AB // CD, AB < CD). Kẻ các đường cao AE, BF của hình thang. Chứng minh rằng DE = CF.

Bài 7 Cho hình thang cân ABCD (AB//CD), E là giao điểm của hai đường chéo. Chứng minh rằng EA = EB, EC = ED.

Bài 8 Trong các tứ giác ABCD, EFGH trên giấy kẻ ô vuông (h.31), tứ giác nào là hình thang cân? Vì sao?

Bài 9 Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy theo thứ tự các điểm D, E sao cho AD = AE

a) Chứng minh rằng BDEC là hình thang cân.

b) Tính các góc của hình thang cân đó, biết rằng góc A = 50^o.

Bài 10 Cho tam giác ABC cân tại A, các đường phân giác BD, CE (D ∈ AC, E ∈ AB). Chứng minh rằng BEDC là hình thang cân có đáy nhỏ bằng cạnh bên.

Bài 11 Hình thang ABCD (AB // CD) có

Chứng minh rằng ABCD là hình thang cân.

Bài 12 Chứng minh định lý: "Hình thang có hai đường chéo bằng nhau là hình thang cân" qua bài toán sau: Cho hình thang ABCD (AB // CD) có AC = BD. Qua B kẻ đường thẳng song song với AC, cắt đường thẳng DC tại tại E. Chứng minh rằng:

a) ΔBDE là tam giác cân.

b) ΔACD = ΔBDC

c) Hình thang ABCD là hình thang cân.

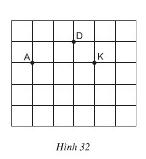
Bài 13 Cho ba điểm A, D, K trên giấy kẻ ô vuông (h.32) Hãy tìm điểm thứ tư M giao điểm của các dòng kẻ sao cho nó cùng với ba diểm đã cho là bốn đỉnh của một hình thang cân.

Bài 14 Hình thang ABCD (AB // CD) có

Chứng minh rằng ABCD là hình thang cân.

Bài 15 Chứng minh định lý: "Hình thang có hai đường chéo bằng nhau là hình thang cân" qua bài toán sau: Cho hình thang ABCD (AB // CD) có AC = BD. Qua B kẻ đường thẳng song song với AC, cắt đường thẳng DC tại tại E. Chứng minh rằng:

a) ΔBDE là tam giác cân.

b) ΔACD = ΔBDC

c) Hình thang ABCD là hình thang cân.

Bài 16 Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy theo thứ tự các điểm D, E sao cho AD = AE

a) Chứng minh rằng BDEC là hình thang cân.

b) Tính các góc của hình thang cân đó, biết rằng góc A = 50^o.

Bài 17 Hình thang ABCD (AB // CD) trên hình 23 có gì đặc biệt ?

Bài 18 Cho hình 24.

a) Tìm các hình thang cân.

b) Tính các góc còn lại của mỗi hình thang cân đó.

c) Có nhận xét gì về hai góc đối của hình thang cân ?

Bài 19 Cho đoạn thẳng CD và đường thẳng m song song với CD (hình 29). Hãy vẽ các điểm A, B thuộc m sao cho ABCD là hình thang có hai đường chéo CA và DB bằng nhau. Sau đó hãy đo các góc C  và góc D của hình thang ABCD đó để dự đoán về dạng của những hình thang có đường chéo bằng nhau.

Bài 20 Tính độ dài các cạnh của hình thang cân ABCD trên giấy kẻ ô vuông (h.30, độ dài của cạnh ô vuông là 1cm).

Xem thêm các bài Bài tập Toán lớp 8 hay, chi tiết khác:

Bài tập Tứ giác

Bài tập Hình thang

Bài tập Đường trung bình của tam giác, của hình thang

Bài tập Đối xứng trục

Bài tập Hình bình hành