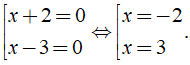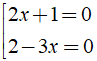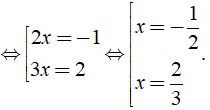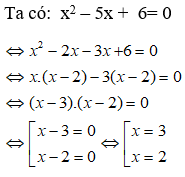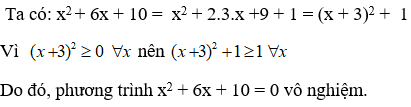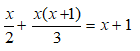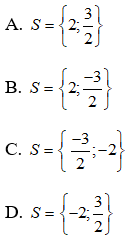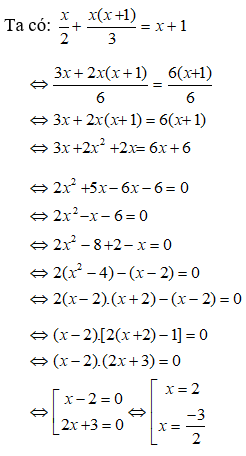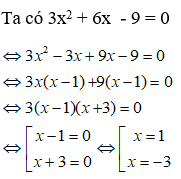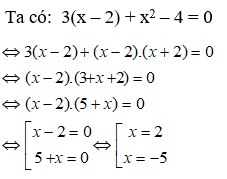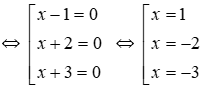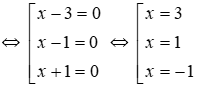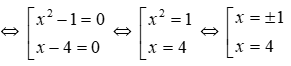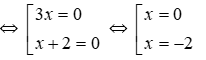50 Bài tập Phương trình tích Toán 8 mới nhất
Với 50 Bài tập Phương trình tích Toán lớp 8 mới nhất được biên soạn bám sát chương trình Toán 8 giúp các bạn học tốt môn Toán hơn.
Tài liệu gồm: 15 bài tập trắc nghiệm, 15 bài tập tự luận có lời giải và 20 bài tập vận dụng. Mời các bạn đón xem:
Bài tập Phương trình tích - Toán 8
I. Bài tập trắc nghiệm
Bài 1: Nghiệm của phương trình ( x + 2 )( x - 3 ) = 0 là?
A. x = - 2. B. x = 3.
C. x = - 2; x = 3. D. x = 2.
Lời giải:
Ta có: ( x + 2 )( x - 3 ) = 0 ⇔
Vậy nghiệm của phương trình là x = - 2; x = 3.
Chọn đáp án C.
Bài 2: Tập nghiệm của phương trình ( 2x + 1 )( 2 - 3x ) = 0 là?
A. S = { - 12 }. B. S = { - 12; 32 }
C. S = { - 12; 23 }. D. S = { 32 }.
Ta có: ( 2x + 1 )( 2 - 3x ) = 0 ⇔
Vậy tập nghiệm của phương trình S = { - 12; 23 }.
Chọn đáp án C.
Bài 3: Nghiệm của phương trình 2x( x + 1 ) = x2 - 1 là?
A. x = - 1.
B. x = ± 1.
C. x = 1.
D. x = 0.
Ta có: 2x( x + 1 ) = x2 - 1 ⇔ 2x( x + 1 ) = ( x + 1 )( x - 1 )
⇔ ( x + 1 )( 2x - x + 1 ) = 0 ⇔ ( x + 1 )( x + 1 ) = 0
⇔ ( x + 1 )2 = 0 ⇔ x + 1 = 0 ⇔ x = - 1.
Vậy phương trình có nghiệm là x = - 1.
Chọn đáp án A.
Bài 4: Giá trị của m để phương trình ( x + 2 )( x - m ) = 4 có nghiệm x = 2 là?
A. m = 1.
B. m = ± 1.
C. m = 0.
D. m = 2.
Phương trình ( x + 2 )( x - m ) = 4 có nghiệm x = 2, thay x = 2 vào phương trình đã cho
Khi đó ta có: ( 2 + 2 )( 2 - m ) = 4 ⇔ 4( 2 - m ) = 4
⇔ 2 - m = 1 ⇔ m = 1.
Vậy m = 1 là giá trị cần tìm.
Chọn đáp án A.
Bài 5: Giá trị của m để phương trình x3 - x2 = x + m có nghiệm x = 0 là?
A. m = 1.
B. m = - 1.
C. m = 0.
D. m = ± 1.
Thay x = 0 vào phương trình x3 - x2 = x + m.
Khi đó ta có: 03 - 02 = 0 + m ⇔ m = 0.
Vậy m = 0 là giá trị cần tìm.
Chọn đáp án C.
Bài 6: Giải phương trình: x2 - 5x + 6 = 0
A. x = 3 hoặc x = 2
B. x= -2 hoặc x = -3
C. x = 2 hoặc x = -3
D. x = -2 hoặc x = 3
Chọn đáp án A
Bài 7: Số nghiệm của phương trình x2 + 6x + 10 = 0
A. 1
B. 2
C. 0
D. Vô nghiệm
Chọn đáp án D
Bài 8: Giải phương trình:
Chọn đáp án B
Bài 9: Giải phương trình : 3x2 + 6x - 9 = 0
A. x = 1
B. x = 1 hoặc x = -3
C. x = 1 hoặc x = -2
D. x = -3 hoặc x = -2
Chọn đáp án B
Bài 10: Giải phương trình: 3(x - 2) + x2 - 4 = 0
A. x = 1 hoặc x = 2
B. x = 2 hoặc x = -5
C. x = 2 hoặc x = - 3
D. Đáp án khác
Vậy nghiệm của phương trình đã cho là x = 2 hoặc x = - 5
Chọn đáp án B
II. Bài tập tự luận có lời giải
Bài 1: Tích các nghiệm của phương trình x3 + 4x2 + x – 6 = 0 là?
Lời giải
Ta có
x3 + 4x2 + x – 6 = 0
⇔ x3 – x2 + 5x2 – 5x + 6x – 6 = 0
⇔ x(x – 1) + 5x(x – 1) + 6(x – 1) = 0
⇔ (x – 1)(x2 + 5x + 6) = 0
⇔ (x – 1)(x2 + 2x + 3x + 6) = 0
⇔ (x – 1)[x(x + 2) + 3(x + 2)] = 0
⇔ (x – 1)(x + 2)(x + 3)= 0
Vậy S = {1; -2; -3} nên tích các nghiệm là 1.(-2).(-3) = 6
Bài 2 Tích các nghiệm của phương trình x3 – 3x2 – x + 3 = 0 là?
Lời giải
Ta có x3 – 3x2 – x + 3 = 0
⇔ (x3 – 3x2) – (x – 3) = 0
⇔ x(x2 – 3) – (x – 3)= 0
⇔ (x – 3)(x2 – 1) = 0
⇔ (x – 3)(x – 1)(x + 1) = 0
Vậy S = {1; -1; 3} nên tích các nghiệm là 1.(-1).3 = -3
Bài 3 Nghiệm lớn nhất của phương trình (x2 – 1)(2x – 1) = (x2 – 1)(x + 3) là?
Lời giải
Ta có (x2 – 1)(2x – 1) = (x2 – 1)(x + 3)
⇔ (x2 – 1)(2x – 1) – (x2 – 1)(x + 3) = 0
⇔ (x2 – 1)(2x – 1 – x – 3) = 0
⇔ (x2 – 1)(x – 4) = 0
Vậy tập nghiệm của phương trình S = {-1; 1; 4}
Nghiệm lớn nhất của phương trình là x = 4
Bài 4 Số nghiệm của phương trình: (x2 + 9)(x – 1) = (x2 + 9)(x + 3) là?
Lời giải
Ta có (x2 + 9)(x – 1) = (x2 + 9)(x + 3)
⇔ (x2 + 9)(x – 1) - (x2 + 9)(x + 3) = 0
⇔ (x2 + 9)(x – 1 – x – 3) = 0
⇔ (x2 + 9)(-4) = 0
⇔ x2 + 9 = 0 ⇔ x2 = -9 (vô nghiệm)
Vậy tập nghiệm của phương trình S = Ø hay phương trình không có nghiệm
Bài 5 Nghiệm nhỏ nhất của phương trình (2x + 1)2 = (x – 1)2 là?
Lời giải
Ta có (2x + 1)2 = (x – 1)2
⇔ (2x + 1 + x – 1)(2x + 1 – x + 1) = 0
⇔ 3x(x + 2) = 0
Vậy tập nghiệm của phương trình S = {0; -2}
Nghiệm nhỏ nhất là x = -2
Bài 6 Giải các phương trình:
a) (3x - 2)(4x + 5) = 0
b) (2,3x - 6,9)(0,1x + 2) = 0
c) (4x + 2)(x2+ 1) = 0
d) (2x + 7)(x - 5)(5x + 1) = 0
Lời giải:
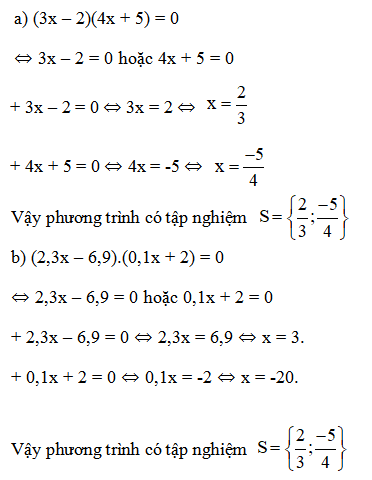

Bài 7 Bằng cách phân tích vế trái thành nhân tử, giải các phương trình sau:
a) 2x(x – 3) + 5(x – 3) = 0;
b) (x2– 4) + (x – 2)(3 – 2x) = 0;
c) x3– 3x2+ 3x – 1 = 0;
d) x(2x – 7) – 4x + 14 = 0;
e) (2x – 5)2– (x + 2)2= 0;
f) x2– x – (3x – 3) = 0.
Lời giải:
a) 2x(x – 3) + 5(x – 3) = 0
⇔ (2x + 5)(x – 3) = 0
⇔ 2x + 5 = 0 hoặc x – 3 = 0
+ 2x + 5 = 0 ⇔2x = -5 ⇔ x = -52
+ x – 3 = 0 ⇔x = 3.
Vậy phương trình có tập nghiệm
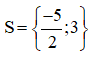
b) (x2– 4) + (x – 2)(3 – 2x) = 0
⇔ (x – 2)(x + 2) + (x – 2)(3 – 2x) = 0
⇔ (x – 2)[(x + 2) + (3 – 2x)] = 0
⇔ (x – 2)(5 – x) = 0
⇔ x – 2 = 0 hoặc 5 – x = 0
+ x – 2 = 0 ⇔ x = 2
+ 5 – x = 0 ⇔ x = 5.
Vậy tập nghiệm của phương trình là S = {2; 5}.
c) x3– 3x2+ 3x - 1 = 0
⇔ (x – 1)3 = 0 (Hằng đẳng thức)
⇔ x – 1 = 0
⇔ x = 1.
Vậy tập nghiệm của phương trình là S={1}.
d) x(2x – 7) – 4x + 14 = 0
⇔ x(2x – 7) – 2(2x – 7) = 0
⇔(x – 2)(2x – 7) = 0
⇔ x – 2 = 0 hoặc 2x – 7 = 0
+ x – 2 = 0 ⇔ x = 2.
+ 2x – 7 = 0 ⇔ 2x = 7 ⇔ x = 72
Vậy tập nghiệm của phương trình là:
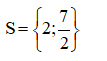
e) (2x – 5)2– (x + 2)2= 0
⇔ [(2x – 5) + (x + 2)].[(2x – 5) – (x + 2)]= 0
⇔ (3x – 3)(x – 7) = 0
⇔ 3x – 3 = 0 hoặc x – 7 = 0
+ 3x – 3 = 0 ⇔3x = 3 ⇔ x = 1.
+ x – 7 = 0 ⇔ x = 7.
Vậy phương trình có tập nghiệm S = {1; 7}.
f) x2– x – (3x – 3) = 0
⇔ x(x – 1) – 3(x – 1) = 0
⇔ (x – 3)(x – 1) = 0
⇔ x – 3 = 0 hoặc x – 1 = 0
+ x – 3 = 0 ⇔ x = 3
+ x – 1 = 0 ⇔ x = 1.
Vậy phương trình có tập nghiệm S = {1; 3}.
Bài 8 Phân tích đa thức P(x) = (x2 – 1) + (x + 1)(x – 2) thành nhân tử.
Lời giải
P(x) = (x2– 1) + (x + 1)(x – 2)
P(x) = (x – 1) (x+1) + (x + 1)(x – 2)
P(x) = (x + 1) (x – 1 + x – 2)
P(x) = (x +1) (2x – 3)
Bài 9 Hãy nhớ lại một tính chất của phép nhân các số, phát biểu tiếp các khẳng định sau:
Trong một tích nếu có một thừa số bằng 0 thì …; ngược lại, nếu tích bằng 0 thì ít nhất một trong các thừa số của tích …
Lời giải
Trong một tích nếu có 1 thừa số bằng 0 thì tích bằng 0; ngược lại, nếu tích bằng 0 thì ít nhất 1 trong các thừa số của tích bằng 0
Bài 10 Giải phương trình:
(x – 1)(x2 + 3x – 2) – (x3 – 1) = 0.
Lời giải
(x – 1)(x2 + 3x – 2) – (x3 – 1) = 0
⇔ (x – 1)(x2 + 3x - 2) - (x - 1)(x2 + x + 1) = 0
⇔ (x – 1)[(x2 + 3x - 2) - (x2 + x + 1)] - 0
⇔ (x – 1)(2x - 3) = 0
⇔ x - 1 = 0 hoặc 2 - 3 = 0
x - 1 = 0 ⇔x = 1
2x - 3 = 0 ⇔x = 32
Vậy tập nghiệm của phương trình là S = {1;32}
III. Bài tập vận dụng
Bài 1 Phân tích đa thức P(x) = (x2 – 1) + (x + 1)(x – 2) thành nhân tử.
Bài 2 Hãy nhớ lại một tính chất của phép nhân các số, phát biểu tiếp các khẳng định sau: Trong một tích nếu có một thừa số bằng 0 thì …; ngược lại, nếu tích bằng 0 thì ít nhất một trong các thừa số của tích …Bài 3 Giải phương trình: (x – 1)(x2 + 3x – 2) – (x3 – 1) = 0.
Bài 4 Giải phương trình (x3 + x2) + (x2 + x) = 0.
Bài 5 Giải các phương trình:
a) (3x - 2)(4x + 5) = 0
b) (2,3x - 6,9)(0,1x + 2) = 0
c) (4x + 2)(x2 + 1) = 0
d) (2x + 7)(x - 5)(5x + 1) = 0
Bài 6 Bằng cách phân tích vế trái thành nhân tử, giải các phương trình sau:
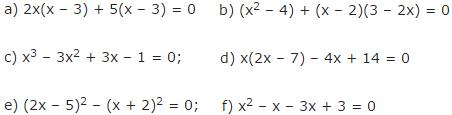
Bài 7 Giải các phương trình:
a) x(2x - 9) = 3x(x - 5)
b, 0,5x(x - 3) = (x - 3)(1,5x - 1)
c) 3x - 15 = 2x(x - 5)
d) 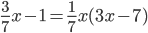
Bài 8 Giải các phương trình:
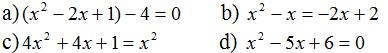
Bài 9 Giải các phương trình:
a) 2x³ + 6x² = x² + 3x
b) (3x - 1)(x² + 2) = (3x - 1)(7x - 10)
Bài 10 Giải các phương trình:
a) (3x−2)(4x+5)=0
b) (2,3x−6,9)(0,1x+2)=0
c) (4x+2)(x2+1)=0
d) (2x+7)(x−5)(5x+1)=0
Xem thêm các bài Bài tập Toán lớp 8 hay, chi tiết khác:
Bài tập Mở đầu về phương trình
Bài tập Phương trình bậc nhất một ẩn và cách giải
Bài tập Phương trình đưa được về dạng ax + b = 0
Xem thêm các chương trình khác:
- Tóm tắt tác phẩm Ngữ văn 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Soạn văn 8 (hay nhất) | Để học tốt Ngữ văn lớp 8 (sách mới)
- Soạn văn 8 (ngắn nhất) | Để học tốt Ngữ văn lớp 8 (sách mới)
- Văn mẫu lớp 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Tác giả - tác phẩm Ngữ văn 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Hóa học 8
- Giải sbt Hóa học 8
- Giải vở bài tập Hóa học 8
- Lý thuyết Hóa học 8
- Các dạng bài tập Hóa học lớp 8
- Giải sgk Vật Lí 8
- Giải sbt Vật Lí 8
- Lý thuyết Vật Lí 8
- Giải vở bài tập Vật lí 8
- Giải sgk Tiếng Anh 8 (sách mới) | Giải bài tập Tiếng Anh 8 Học kì 1, Học kì 2
- Giải sgk Tiếng Anh 8 | Giải bài tập Tiếng Anh 8 Học kì 1, Học kì 2 (sách mới)
- Giải sbt Tiếng Anh 8 (sách mới) | Sách bài tập Tiếng Anh 8
- Giải sbt Tiếng Anh 8 (thí điểm)
- Giải sgk Tin học 8 | Giải bài tập Tin học 8 Học kì 1, Học kì 2 (sách mới)
- Giải sgk Lịch Sử 8 | Giải bài tập Lịch sử 8 Học kì 1, Học kì 2 (sách mới)
- Lý thuyết Lịch sử 8 (sách mới) | Kiến thức trọng tâm Lịch sử 8
- Giải vở bài tập Lịch sử 8
- Giải Tập bản đồ Lịch sử 8
- Đề thi Lịch Sử 8
- Giải vở bài tập Sinh học 8
- Giải sgk Sinh học 8
- Lý thuyết Sinh học 8
- Giải sgk Giáo dục công dân 8 | Giải bài tập Giáo dục công dân 8 Học kì 1, Học kì 2 (sách mới)
- Lý thuyết Giáo dục công dân 8 (sách mới) | Kiến thức trọng tâm GDCD 8
- Lý thuyết Địa Lí 8 (sách mới) | Kiến thức trọng tâm Địa Lí 8
- Giải sgk Địa Lí 8 | Giải bài tập Địa Lí 8 Học kì 1, Học kì 2 (sách mới)
- Giải Tập bản đồ Địa Lí 8
- Đề thi Địa lí 8