50 Bài tập Liên hệ giữa thứ tự và phép cộng Toán 8 mới nhất
Với 50 Bài tập Liên hệ giữa thứ tự và phép cộng Toán lớp 8 mới nhất được biên soạn bám sát chương trình Toán 8 giúp các bạn học tốt môn Toán hơn.
Tài liệu gồm: 15 bài tập trắc nghiệm, 15 bài tập tự luận có lời giải và 20 bài tập vận dụng. Mời các bạn đón xem:
Bài tập Liên hệ giữa thứ tự và phép cộng - Toán 8
I. Bài tập trắc nghiệm
Bài 1: Trong các khẳng định sau đây, khẳng định nào đúng?
4 + ( - 3 ) ≤ 5 ( 1 )
6 + ( - 2 ) ≤ 7 + ( - 2 ) ( 2 )
24 + ( - 5 ) > 25 + ( - 5 ) ( 3 )
A. ( 1 ),( 2 ),( 3 )
B. ( 1 ),( 3 )
C. ( 1 ),( 2 )
D. ( 2 ),( 3 )
+ Ta có: -3 < 1 nên 4 + (-3) < 4 + 1 hay 4 + (-3) < 5
Khẳng định ( 1 ) đúng.
+ Ta có: 6 < 7 nên 6 + (-2) < 7 + (-2)
Khẳng định ( 2 ) đúng.
+ Ta có: 24 < 25 ⇒ 24 + ( - 5 ) < 25 + ( - 5 )
→ Khẳng định ( 3 ) sai.
Chọn đáp án C.
Bài 2: Cho a - 3 > b - 3. So sánh hai số a và b
A. a ≥ b
B. a < b
C. a > b
D. a ≤ b
Ta có a - 3 > b - 3 ⇒ ( a - 3 ) + 3 > ( b - 3 ) + 3 ⇔ a > b
Chọn đáp án C.
Bài 3: Cho a > b. So sánh 5 - a với 5 - b
A. 5 - a ≥ 5 - b.
B. 5 - a > 5 - b.
C. 5 - a ≤ 5 - b.
D. 5 - a < 5 - b.
Ta có: a > b ⇒ - a < - b ⇔ 5 + ( - a ) < 5 + ( - b ) hay 5 - a < 5 - b.
Chọn đáp án D.
Bài 4: Một Ampe kế có giới hạn đo là 25 ampe. Gọi x( A ) là số đo cường độ dòng điện có thể đo bằng Ampe kế. Khẳng định nào sau đây đúng?
A. x ≤ 25
B. x < 25
C. x > 25
D. x ≥ 25
Một Ampe kế đo cường độ dòng điện thì cường độ dòng điện tối đa mà Ampe đo được là giới hạn đo của ampe kế đó.
Khi đó: x ≤ 25
Chọn đáp án A.
Bài 5: Cho a > b, c > d. Khẳng định nào sau đây đúng?
A. a + d > b + c
B. a + c > b + d
C. b + d > a + c
D. a + b > c + d
Theo giả thiết ta có: a > b, c > d ⇒ a + c > b + d.
Chọn đáp án B.
Bài 6: Cho a < b. So sánh: a + (-3) và b + 3
A. a + (-3) = b + 3
B. a + (-3) > b +3
C. a + (-3) < b +3
D. Không so sánh được.
* Ta có: a < b nên a + (-3) < b + (-3) (1)
Lại có: - 3 < 3 nên b +(-3) < b +3 (2)
* Từ (1) và (2) suy ra a + (-3) < b +3
Chọn đáp án C
Bài 7: Cho a + 2 < b – 3 . So sánh a và b?
A. a < b
B. a > b
C. a = b
D. Chưa thể kết luận
Ta có : a + 2 < b – 3 nên a + 2+ (-2) < b - 3 + (-2)
Hay a < b – 5 (1)
Lại có: -5 < 0 nên b – 5 < b (2)
Từ (1) và (2) suy ra: a < b
Chọn đáp án A
Bài 8: Cho các khẳng định sau:
(1): 3 + ( -10) < 4 + (- 10)
(2): (-2) + (-15) > (-2) + (-13)
(3): 4 – 9 < -5 - 9
Hoỉ có bao nhiêu khẳng định đúng?
A. 0
B. 1
C. 2
D. 3
(1): Vì 3 < 4 nên 3 + ( -10) < 4 + (- 10)
Do đó (1) đúng.
(2): vì (- 15) < (-13) nên (-2) + (-15) < (-2) + (-13)
Suy ra (2) sai
(3): Ta có: 4 > - 5 nên 4+ (-9) > - 5 + (- 9) hay 4 – 9 > -5 - 9
Suy ra (3) sai
Vậy chỉ có 1 khẳng định đúng
Chọn đáp án B
Bài 9: Cho a < b - 1. So sánh a và b.
A. Chưa thể kết luận
B. a = b
C. a > b
D. a < b
Ta có: -1 < 0 nên b + (-1) < b + 0 hay b - 1 < b (1)
Lại có: a < b – 1 (giả thiết ) (2 )
Từ (1) và (2) suy ra: a < b
Chọn đáp án D
Bài 10: Ta có:
(1) -2000 < -2001
(2) suy ra: -2000 + a < -2001 + a
Bài giải trên có sai không? Nếu sai thì sai từ bước mấy?
A. Bài giải đúng
B. Sai bước 1
C. Sai bước 2
D. Tùy giá trị của a.
Ta có: -2000 > -2001 nên bước (1) sai
Chọn đáp án B
II. Bài tập tự luận có lời giải
Bài 1: Cho a > b khi đó?
Lời giải
Từ a > b, cộng -b vào hai vế ta được a - b > b - b, tức là a - b > 0.
Bài 2 Cho a > 1 > b, chọn khẳng định không đúng?
Lời giải
Từ a > b, cộng -b vào hai vế ta được a - b > b - b, tức là a - b > 0.
Do đó D đúng, B sai.
Ngoài ra A, C đúng vì:
Cộng cả hai vế của bất đẳng thức a > 1 với (-1) ta được:
a + (-1) > 1 + (-1) hay a - 1 > 0.
Cộng cả hai vế của bất đẳng thức 1 > b với -b ta được:
1 + (-b) > b + (-b) hay 1 - b > 0.
Đáp án cần chọn là: B
Bài 3 So sánh m và n biết m - 
Lời giải
Ta có: m - 

Bài 4 So sánh m và n biết m + 
Lời giải
Ta có: m + 

Bài 5 Cho a + 8 < b. So sánh a - 7 và b - 15?
Lời giải
Cộng cả hai vế của bất đẳng thức a + 8 < b với (-15) ta được
a + 8 < b ⇒ a + 8 - 15 < b - 15 ⇒ a - 7 < b - 15
Bài 6 Cho a - 3 < b. So sánh a + 10 và b + 13?
Lời giải
Cộng cả hai vế của bất đẳng thức a - 3 < b với 13 ta được:
a - 3 < b ⇒ a - 3 + 13 < b + 13 ⇒ a + 10 < b + 13.
Bài 7 Mỗi khẳng định sau đúng hay sai? Vì sao?
a) (-2) + 3 ≥ 2;
b) -6 ≤ 2.(-3);
c) 4 + (-8) < 15 + (-8);
d) x2+ 1 ≥ 1.
Lời giải:
(Kí hiệu: VP = vế phải; VT = vế trái)
a) Ta có: (-2) + 3 = 1
Vì 1 < 2 nên (-2) + 3 < 2.
Do đó khẳng định (-2) + 3 ≥ 2 là sai.
b) Ta có: 2.(-3) = -6
⇒ Khẳng định -6 ≤ 2.(-3) là đúng.
c) Ta có: 4 + (-8) = -4
15 + (-8) = 7
Vì -4 < 7 nên 4 + (-8) < 15 + (-8)
Do đó khẳng định c) đúng
d) Với mọi số thực x ta có: x2≥ 0
⇒ x2 + 1 ≥ 1
⇒ Khẳng định d) đúng với mọi số thực x.
Bài 8 Cho a < b, hãy so sánh:
a) a + 1 và b + 1 ;
b) a – 2 và b – 2
Lời giải:
a) a < b
⇒ a + 1 < b + 1
(Cộng cả hai vế của BĐT với 1).
c) a < b
⇒ a + (-2) < b + (-2)
(Cộng cả hai vế của BĐT với -2).
hay a – 2 < b – 2.
Bài 9 So sánh a và b nếu:
a) a – 5 ≥ b – 5 ; b) 15 + a ≤ 15 + b
Lời giải:
a) Vì a – 5 ≥ b – 5
=> a – 5 + 5 ≥ b – 5 + 5 (cộng 5 vào hai vế)
=> a ≥ b
b) 15 + a ≤ 15 + b
=> 15 + a + (-15) ≤ 15 + b (-15) (cộng -15 vào hai vế)
=> a ≤ b
III. Bài tập vận dụng
Bài 1 Một biển báo giao thông với nền trắng, số 20 màu đen, viền đỏ (xem minh họa ở hình bên) cho biết vận tốc tối đa mà các phương tiện giao thông được đi trên quãng đường có biển quy định là 20km/h. Nếu một ô tô đi trên đường đó có vận tốc là a (km/h) thì a phải thỏa mãn điều kiện nào trong các điều kiện sau? a > 20 ; a < 20 ; a ≤ 20 ; a ≥ 20
Bài 2 So sánh a và b nếu:
a) a – 5 ≥ b – 5 ; b) 15 + a ≤ 15 + b
Bài 3 Cho a < b, hãy so sánh:
a) a + 1 và b + 1 ;
b) a – 2 và b – 2
Bài 4 Mỗi khẳng định sau đúng hay sai? Vì sao?
a) (-2) + 3 ≥ 2;
b) -6 ≤ 2.(-3);
c) 4 + (-8) < 15 + (-8);
d) x2 + 1 ≥ 1.
Bài 5 Dựa vào thứ tự √2 và 3, hãy so sánh √2+ 2 và 5.
Bài 6 So sánh - 2004 + (- 777) và - 2005 + (- 777) mà không tính giá trị của từng biểu thức.
a) Khi cộng - 3 và cả hai vế của bất đẳng thức - 4 < 2 thì được bất đẳng thức nào ?
b) Dự đoán kết quả: Khi cộng số c vào cả hai vế của bất đẳng thức - 4 < 2 thì được bất đẳng thức nào ?
Bài 7 So sánh a và b nếu:
a) a−5≥b–
b)
Bài 8 Cho tam giác ABC. Các khẳng định sau đúng hay sai?
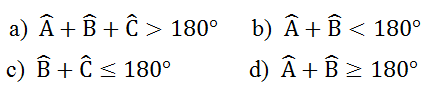
a) So sánh (-2).3 và -4,5.
b) Từ kết quả câu a) hãy suy ra các bất đẳng thức sau:
(-2).30 < -45 ; (-2).3 + 4,5 < 0
Xem thêm các bài Bài tập Toán lớp 8 hay, chi tiết khác:
Bài tập Liên hệ giữa thứ tự và phép nhân có đáp án
Bài tập Bất phương trình một ẩn
Xem thêm các chương trình khác:
- Tóm tắt tác phẩm Ngữ văn 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Soạn văn 8 (hay nhất) | Để học tốt Ngữ văn lớp 8 (sách mới)
- Soạn văn 8 (ngắn nhất) | Để học tốt Ngữ văn lớp 8 (sách mới)
- Văn mẫu lớp 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Tác giả - tác phẩm Ngữ văn 8 (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Giải sgk Hóa học 8
- Giải sbt Hóa học 8
- Giải vở bài tập Hóa học 8
- Lý thuyết Hóa học 8
- Các dạng bài tập Hóa học lớp 8
- Giải sgk Vật Lí 8
- Giải sbt Vật Lí 8
- Lý thuyết Vật Lí 8
- Giải vở bài tập Vật lí 8
- Giải sgk Tiếng Anh 8 (sách mới) | Giải bài tập Tiếng Anh 8 Học kì 1, Học kì 2
- Giải sgk Tiếng Anh 8 | Giải bài tập Tiếng Anh 8 Học kì 1, Học kì 2 (sách mới)
- Giải sbt Tiếng Anh 8 (sách mới) | Sách bài tập Tiếng Anh 8
- Giải sbt Tiếng Anh 8 (thí điểm)
- Giải sgk Tin học 8 | Giải bài tập Tin học 8 Học kì 1, Học kì 2 (sách mới)
- Giải sgk Lịch Sử 8 | Giải bài tập Lịch sử 8 Học kì 1, Học kì 2 (sách mới)
- Lý thuyết Lịch sử 8 (sách mới) | Kiến thức trọng tâm Lịch sử 8
- Giải vở bài tập Lịch sử 8
- Giải Tập bản đồ Lịch sử 8
- Đề thi Lịch Sử 8
- Giải vở bài tập Sinh học 8
- Giải sgk Sinh học 8
- Lý thuyết Sinh học 8
- Giải sgk Giáo dục công dân 8 | Giải bài tập Giáo dục công dân 8 Học kì 1, Học kì 2 (sách mới)
- Lý thuyết Giáo dục công dân 8 (sách mới) | Kiến thức trọng tâm GDCD 8
- Lý thuyết Địa Lí 8 (sách mới) | Kiến thức trọng tâm Địa Lí 8
- Giải sgk Địa Lí 8 | Giải bài tập Địa Lí 8 Học kì 1, Học kì 2 (sách mới)
- Giải Tập bản đồ Địa Lí 8
- Đề thi Địa lí 8
