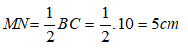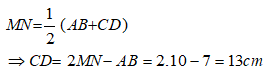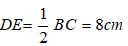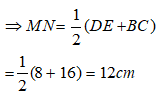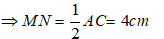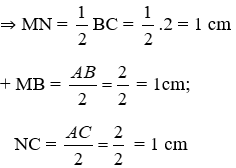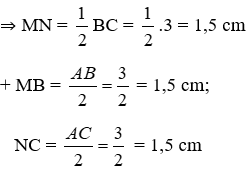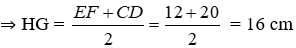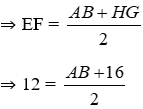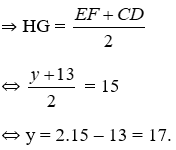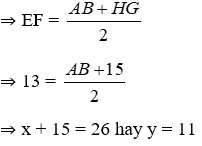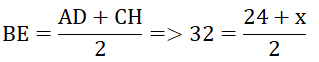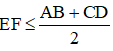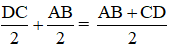Đường trung bình của tam giác, của hình thang, các dạng bài tập và cách giải

Đường trung bình của tam giác, của hình thang, các dạng bài tập và cách giải

A. Lý thuyết về đường trung bình

I. Đường trung bình của tam giác

a) Định nghĩa đường trung bình của tam giác:

Đường trung bình của tam giác là đoạn thẳng nối trung điểm của hai cạnh tam giác đó.

b) Định lý 1: Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.

c) Định lý 2: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh thứ ba.

Xét hình vẽ:

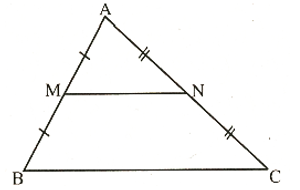
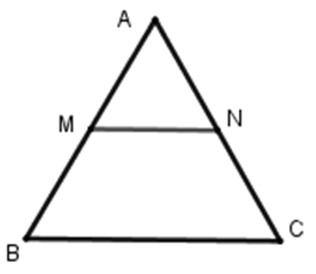
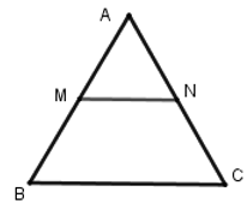
Tam giác ABC có:

M là trung điểm AB

N là trung điểm AC

Nên MN là đường trung bình của tam giác ABC

II. Đường trung bình của hình thang

a) Định nghĩa: Đường trung bình của hình thang là đoạn thẳng nối hai trung điểm của hai cạnh bên hình thang.

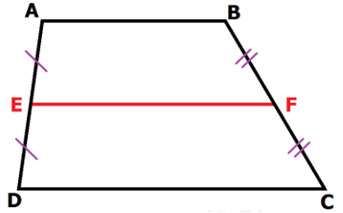
ABCD là hình thang, AB // CD

E là trung điểm AD, F là trung điểm BC

EF là đường trung bình của hình thang ABCD.

b) Định lí 2: Đường thẳng đi qua trung điểm của cạnh bên thứ nhất và song song với cạnh đáy thì nó đi qua trung điểm của cạnh bên thứ hai của hình thang.

c) Định lí 3: Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng hai đáy.

Xét hình thang ABCD có đường trung bình là FE

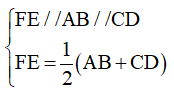
B. Các dạng bài tập về đường trung bình

Dạng 1. Sử dụng định nghĩa và định lý về đường trung bình của tam giác để chứng minh

Phương pháp giải: Sử dụng định nghĩa, định lý để suy ra điều cần chứng minh.

Ví dụ: Cho tam giác ABC, có AM là trung tuyến ứng với BC. Trên cạnh AB lấy điểm D và E sao cho AD = DE = EB. Đoạn CD cắt AM tại I. Chứng minh:

a) EM song song với DC;

b) I là trung điểm AM;

c) DC = 4DI.

Lời giải:

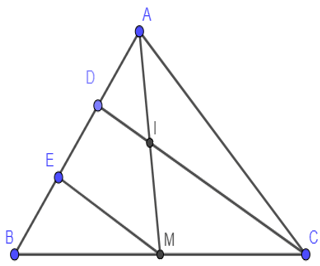
a) Vì ED = EB nên E là trung điểm của BD

Lại có M là trung điểm của BC

Suy ra EM là đường trung bình của tam giác BCD

=> EM // CD

b) Xét tam giác AEM có:

Ta có: AD = DE nên D là trung điểm AE.

Lại có I ∈ DC => DI // EM (do DC // EM)

Do đó: DI đi qua trung điểm AM

=> I là trung điểm của AM

c) Từ câu a ta có: EM là đường trung bình của tam giác BCD

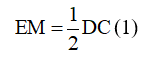
Lại có I là trung điểm của AM, D là trung điểm của AE

=> DI là đường trung bình của tam giác AEM

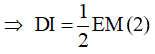
Từ (1) và (2) =>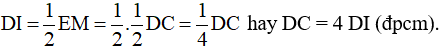

Dạng 2. Sử dụng định lý đường trung bình của hình thang để chứng minh

Phương pháp giải: Sử dụng định nghĩa và các định lý liên quan đến đường trung bình của hình thang để chứng minh.

Ví dụ: Cho hình thang ABCD (AB // CD). Các đường phân giác ngoài của 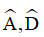cắt nhau tại E, cắc đường phân giác ngoài 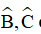cắt nhau tại F. Chứng minh:

a) EF song song AB và CD.

b) EF có độ dạng bằng nửa chu vi hình thang ABCD.

Lời giải:

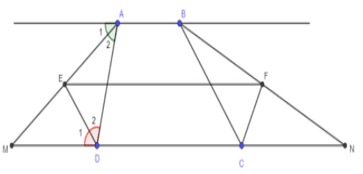
a) Vì AE là phân giác góc ngoài của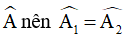

Vì DE là phân giác góc ngoài của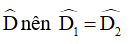

Mà 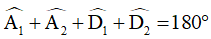(hai góc trong cùng phía)

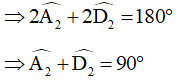
Xét tam giác AED có: 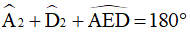(tính chất tổng ba góc trong một tam giác)

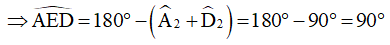
=> DE = AE

Gọi AE ∩ DC = M

ΔADM có DE vừa là đường cao vừa là đường phân giác nên ΔADM cân tại D

Nên DE là đường trung tuyến của ΔADM

=> E là trung điểm của AM.

Gọi BF ∩ DC = N

Chứng minh tương tự có điểm F là trung điểm BN

Lại có tứ giác ABNM có AB // MN (AB // CD) nên ABNM là hình thang

Mà có E, F lần lượt là trung điểm của AM và BN

Nên EF là đường trung bình của hình thang ABNM

=> EF // AB // MM

Hay EF // AB // CD

b) Vì EF là đường trung bình của hình thang ABNM

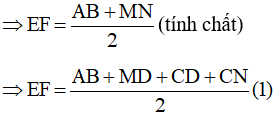
Mà MD = AD (do tam giác AMD cân tại D); CN = BC (do tam giác BCN cân tại C) nên thay vào (1) ta có:

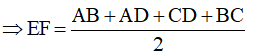
Vậy độ dài EF bằng nửa chu vi tứ giác ABCD.

Dạng 3. Sử dụng phối hợp đường trung bình của tam giác và đường trung bình của hình thang để chứng minh.

Phương pháp giải: Sử dụng kết hợp các định nghĩa định lý về đường trung bình để chứng minh bài toán

Ví dụ: Cho hình thang ABCD (AB // CD, AB < CD) . Gọi M, N, P, Q lần lượt là trung điểm của AD, BD, AC, BC. Chứng minh:

a) M, N ,P, Q cùng nằm trên một đường thẳng

b)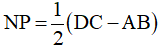

Lời giải:

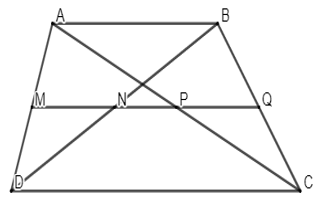
a) Ta có M là trung điểm của AD, Q là trung điểm BC

=> MQ là đường trung bình của hình thang ABCD

=> MQ // AB // CD (1)

M là trung điểm của AD, N là trung điểm của BD

=> MN là đường trung bình của tam giác DAB

=> MN // AB (2)

P là trung điểm của AC, Q là trung điểm của BC

=> PQ là đường trung bình của tam giác ABC

=> PQ // AB (3)

Từ (1), (2) , (3) => MN // MQ // QP // AB

=> bốn điểm M, N, P, Q thẳng hàng

=> M, N, P, Q thuộc cùng một đường thẳng

b) Đặt AB = a; CD = b

Vì MQ là đường trung bình của hình thang ABCD

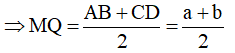
Lại có MN, PQ lần lượt là đường trung bình của tam giác ABD và ABC

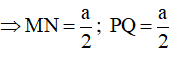
Ta có:

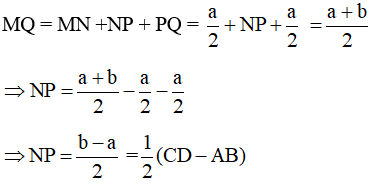
C. Bài tập về đường trung bình

I. Bài tập trắc nghiệm

Bài 1: Cho tam giác ABC có D, E lần lượt là trung điểm của AB, AC. Phát biểu nào sau đây sai?

A. DE là đường trung bình của tam giác ABC.

B. DE song song với BC.

C. DECB là hình thang cân.

D. DE có độ dài bằng nửa BC.

Lời giải:

Xét tam giác ABC có D, E lần lượt là trung điểm của AB, AC

⇒ DE là đường trung bình của tam giác ABC

Hay DE//BC và DE = $\frac{1}{2}BC$

+ Hình thang cân là hình thang có hai góc kề một cạnh bằng nhau và hai cạnh bên bằng nhau nhưng bài toán này hai góc kề một cạnh đáy không bằng nhau

→ Đáp án C sai.

Chọn đáp án C.

Bài 2: Cho tam giác ABC có D, E lần lượt là trung điểm của AB, AC và DE = 4cm. Biết đường cao AH = 6cm. Diện tích của tam giác ABC là?

A. S = 24( cm² )

B. S = 16( cm² )

C. S = 48( cm² )

D. S = 32( cm² )

Lời giải:

Xét tam giác ABC có D, E lần lượt là trung điểm của AB, AC

⇒ DE là đường trung bình của tam giác ABC

Hay DE//BC và DE = $\frac{1}{2}BC$ ⇒ BC = 2DE = 2.4 = 8( cm )

Khi đó ta có: S = $\frac{1}{2}$AH.BC = $\frac{1}{2}$.6.8 = 24( cm² )

Chọn đáp án A.

Bài 3: Chọn phát biểu đúng

A. Đường trung bình của hình thang là đoạn thẳng nối hai trung điểm của hai cạnh bên của hình thang.

B. Đường trung bình của hình thang là đoạn thẳng nối hai trung điểm của hai cạnh đối của hình thoi.

C. Đường trung bình của hình thang thì song song với hai đáy và bằng tổng hai hai đáy.

D. Một hình thang có thể có một hoặc nhiều đường trung bình.

Lời giải:

Định nghĩa: Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang.

→ Đáp án A đúng.

+ Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng của hai đáy.

+ Một hình thang thì chỉ có 1 đường trung bình duy nhất.

Chọn đáp án A.

Bài 4: Với a,b,h lần lượt là độ dài đáy lớn, đáy nhỏ và chiều cao của hình thang thì công thức diện tích của hình thang là ?

A. S = ( a + b )h

B. S = $\frac{1}{2}$( a + b )h

C. S = $\frac{1}{3}$( a + b )h

D. S = $\frac{1}{4}$( a + b )h

Lời giải:

Diện tích hình thang bằng nửa tổng độ dài hai đáy nhân với đường cao của hình thang,

⇒ S = $\frac{1}{2}$( a + b )h

Chọn đáp án B.

Bài 5: Cho tam giác ABC, gọi M, N và P lần lượt là trung điểm của AB, AC và BC. Hỏi có bao nhiêu hình thang trong hình vẽ ?

A. 7

B. 6

C. 8

D. 9

Lời giải:

* Ta có: M và N lần lượt là trung điểm của AB và AC nên MN là đường trung bình của tam giác ABC.

Suy ra: MN// BC

Do đó, tứ giác MNCP, tứ giác MNPB và tứ giác MNCB là hình thang.

* Tương tự, có MP là đường trung bình của tam giác nên MP// AC

NP là đường trung bình của tam giác nên NP // AB.

Các tứ giác: MPNA; MPCN và MPCA ; NPBA là hình thang.

Vậy có tất cả 7 hình thang

Chọn đáp án A

Bài 6: Cho tam giác ABC vuông tại A có AB = 6cm, AC = 8cm. Gọi M và N lần lượt là trung điểm của AB và AC. Tính MN?

A. 4cm

B.10cm

C. 5 cm

D. 7cm

Lời giải:

Áp dụng định lí Pytago vào tam giác vuông ABC ta có:

BC² = AB² + AC² = 6² + 8² = 100

Suy ra: BC = 10cm

Do M và N lần lượt là trung điểm của AB và AC nên MN là đường trung bình của tam giác ABC

Suy ra:

Chọn đáp án C

Bài 7: Cho hình thang ABCD; AB // CD có M và N lần lượt là trung điểm của AD và BC. Biết AB = 7cm và MN = 10cm. Tính CD.

A. 7cm

B. 17 cm

C. 4cm

D. 13cm

Lời giải:

Xét hình thang ABCD có M và N lần lượt là trung điểm của AD và BC.

Suy ra, MN là đường trung bình của hình thang

Do đó:

Chọn đáp án D

Bài 8: Cho hình thang ABCD có M, N theo thứ tự là trung điểm của AD; AC; cạnh MN cắt BC tại P. Biết CD = 10cm và NP = 3cm. Tính AB

A. 5cm

B. 6cm

C. 7cm

D. 6,5 cm

Lời giải:

Xét tam giác ACD có M và N lần lượt là trung điểm của AD và AC nên: MN// CD

Vì MN// CD và AB// CD nên: MN// AB

Suy ra: NP // AB

Xét tam giác ABC có N là trung điểm của AC và NP// AB nên P là trung điểm của BC

Suy ra: NP là đường trung bình của tam giác ABC

Do đó: AB = 2NP = 2.3 = 6cm

Chọn đáp án B

Bài 9: Cho tam giác ABC có BC = 16 cm. Gọi D và E lần lượt là trung điểm của AB và AC. Gọi M và N lần lượt là trung điểm của BD và EC. Tính MN?

A. 9cm

B. 8cm

C. 10cm

D. 12cm

Lời giải:

* Xét tam giác ABC có D và E lần lượt là trung điểm của AB và AC nên DE là đường trung bình của tam giác.

Suy ra: DE// BC và

* Xét tứ giác DECB có DE // BC nên DECB là hình thang.

Lại có: M và N lần lượt là trung điểm của BD và EC nên MN là đường trung bình của hình thang .

Chọn đáp án D

Bài 10: Cho tam giác ABC có AB = 6cm, AC = 8cm và BC = 10cm. Gọi M là trung điểm của BC. Từ M kẻ đường thẳng vuông góc với AB cắt AB tại N. Tính MN?

A. 4cm

B. 5cm

C. 6cm

D. 3cm

Lời giải:

* Ta có: AB² + AC² = BC² (6² + 8² = 10² = 100)

Suy ra: tam giác ABC vuông tại A

⇒ AB ⊥ AC

* Lại có: MN ⊥ AB nên MN // AC.

* Vì MN // AC và M là trung điểm của BC nên N là trung điểm của AB.

Khi đó, MN là đường trung bình của tam giác ABC .

Chọn đáp án A

Bài 11: Cho ΔABC đều, cạnh 2cm; M, N là trung điểm của AB và AC. Chu vi của tứ giác MNCB bằng

A. 5cm

B. 6cm

C. 4 cm

D. 7 cm

Lời giải:

+ M, N là trung điểm của AB và AC nên MN là đường trung bình của tam giác ABC

+ Chu vi tứ giác MNCB là P = MN + BC + MB + NC = 1 + 1 + 1 + 2 = 5cm

Đáp án cần chọn là: A

Bài 12: Cho ΔABC đều, cạnh 3cm; M, N là trung điểm của AB và AC. Chu vi của tứ giác MNCB bằng

A. 8cm

B. 7,5 cm

C. 6 cm

D. 7 cm

Lời giải:

+ M, N là trung điểm của AB và AC nên MN là đường trung bình của tam giác ABC

+ Chu vi tứ giác MNCB là:

P = MN + BC + MB + NC = 1,5 + 1,5 + 1,5 + 3 = 7,5 cm

Đáp án cần chọn là: B

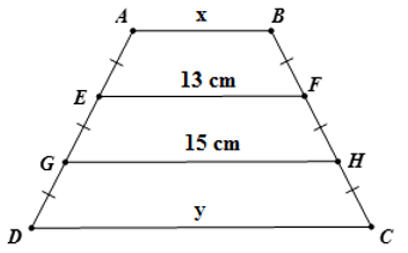
Bài 13: Tìm x, y trên hình vẽ, trong đó AB // EF // GH // CD. Hãy chọn câu đúng.

A. x = 8cm, y = 16 cm

B. x = 18 cm, y = 9 cm

C. x = 18 cm, y = 8 cm

D. x = 16 cm, y = 8 cm

Lời giải:

+ Vì AB // EF // GH // CD nên các tứ giác EFCD, ABHG là hình thang

+ Từ hình vẽ ta có GH là đường trung bình của hình thang EFCD

Hay x = 16cm.

+ Lại có EF là đường trung bình của hình thang ABHG

⇒ AB + 16 = 24 hay y = 8 cm

Vạy x = 16cm, y = 8cm

Đáp án cần chọn là: D

Bài 14: Tính x, y trên hình vẽ, trong đó AB // EF // GH // CD. Hãy chọn câu đúng.

A. x = 15; y = 17

B. x = 11; y = 17

C. x = 12; y = 16

D. x = 17; y = 11

Lời giải:

+ Vì AB // EF // GH // CD nên các tứ giác EFCD, ABHG là hình thang

+ Từ hình vẽ ta có GH là đường trung bình của hình thang EFCD

Vậy y = 17.

+ Lại có EF là đường trung bình của hình thang ABHG

Vạy x = 11cm, y = 17cm

Đáp án cần chọn là: B

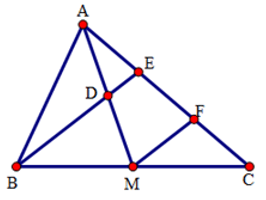
Bài 15: Cho tam giác ABC, đường trung tuyến AM. Gọi D là trung điểm của AM, E là giao điểm của BD và AC, F là trung điểm của EC. Chọn câu đúng trong các câu sau:

A. AE = $\frac{1}{2}$EC

B. AE = 2EC

C. FC = AF

D. MF = BE

Lời giải:

Xét tam giác BEC có BM = MC, EF = FC nên MF là đường trung bình của tam giác BEC. Do đó MF // BE.

Xét tam giác ÀM có AD = DM, DE // MF nên DE là đường trung bình cuả tam giác AMF. Do đó AE = EF.

Do đó AE = EF = FC nên AE = $\frac{1}{2}$EC

Đáp án cần chọn là: A

II. Bài tập tự luận có lời giải

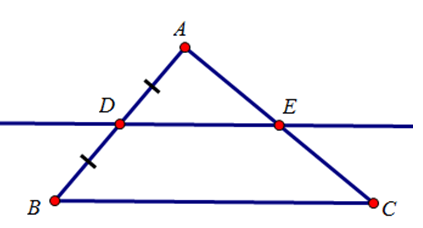
Bài 1: Vẽ tam giác ABC bất kì rồi lấy trung điểm D của AB. Qua D vẽ đường thẳng song song với BC, đường thẳng này cắt AC ở E. Bằng quan sát, hãy nêu dự đoán về vị trí của điểm E trên cạnh AC.

Lời giải

Dự đoán: E là trung điểm cạnh AC

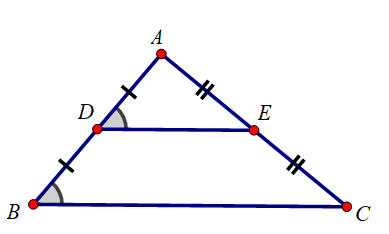
Bài 2 Vẽ tam giác ABC bất kì rồi lấy trung điểm D của AB, trung điểm E của AC. Dùng thước đo góc và thước chia khoảng để kiểm tra rằng 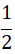$\widehat{ADE}=\hat{B}$ và DE = BC.

Lời giải

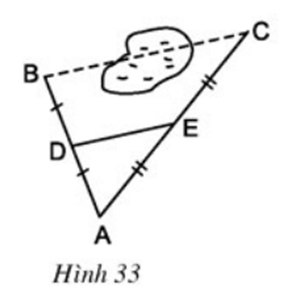
Bài 3 Tính độ dài đoạn BC trên hình 33.

Lời giải

BC = 2 DE

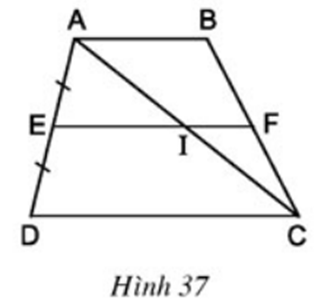
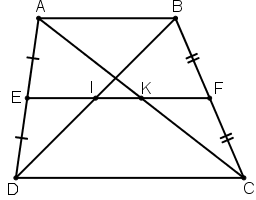
Bài 4 Cho hình thang ABCD (AB // CD). Qua trung điểm E của AD kẻ đường thẳng song song với hai đáy, đường thẳng này cắt AC ở I, cắt BC ở F (h.37). Có nhận xét gì về vị trí của điểm I trên AC, điểm F trên BC ?

Lời giải

Áp dụng định lí 1 đường trung bình của tam giác

ΔADC có E là trung điểm AD và EI song song với cạnh DC

⇒ Điểm I là trung điểm AC

ΔABC có I là trung điểm AC và FI song song với cạnh AB

⇒ điểm F là trung điểm BC

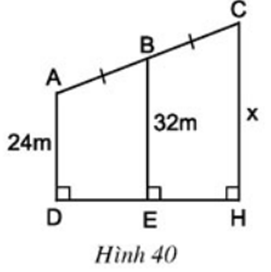
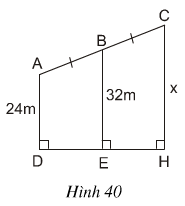
Bài 5 Tính x trên hình 40.

Lời giải:

Dựa vào hình vẽ ta thấy rằng AD ⊥ DH, CH ⊥ DH, BE ⊥ DH

Suy ra, AD // BE // CH do đó ADHC là hình thang.

Ta thấy rằng, B là trung điểm của AC và BE // AD // CH

Suy ra BE là đường trung bình của hình thang ADHC, ta có:

⇒ 64 = 24 + x ⇒ x = 40

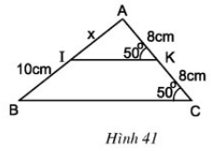
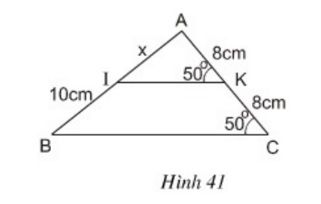
Bài 6 Tính x trên hình 41.

Lời giải:

+ K̂ = Ĉ (= 50º)

⇒ IK // BC (Vì có hai góc đồng vị bằng nhau)

+ KA = KC (= 8cm) nên K là trung điểm AC

Đường thẳng IK đi qua trung điểm cạnh AC và song song với cạnh BC nên đi qua trung điểm cạnh AB

⇒ I là trung điểm AB

⇒ IA = IB hay x = 10cm.

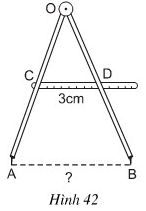
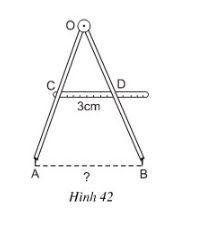
Bài 7 Tính khoảng cách AB giữa hai mũi của compa trên hình 42, biết rằng C là trung điểm của OA, D là trung điểm của OB và CD = 3cm.

Lời giải:

Ta có: CO = CA (gt)

DO = DB (gt)

⇒ CD là đường trung bình của ΔOAB

⇒ AB = 2CD = 2.3 = 6cm.

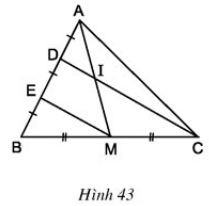
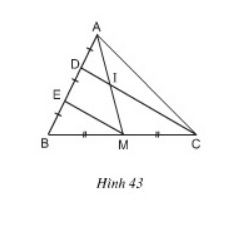
Bài 8 Cho hình 43. Chứng minh rằng AI = IM.

Lời giải:

ΔBDC có BE = ED và BM = MC

⇒ EM là đường trung bình của ΔBDC

⇒ EM // DC hay EM // DI.

ΔAEM có DI // EM (cmt) và AD = DE (gt)

⇒ IA = IM (Theo định lý 1)

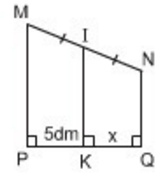
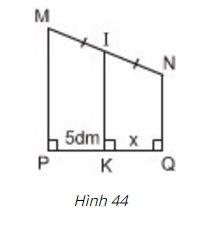
Bài 9 Tìm x trên hình 44.

Hình 44

Lời giải:

* Ba đường thẳng MP, NQ và IK cùng vuông góc với PQ

=> MP// IK// NQ

=> Tứ giác MPQN là hình thang

Do đường thẳng IK đi qua trung điểm cạnh bên MN và song song với hai đáy nên K là trung điểm PQ.

Nên PK = KQ =5dm

Vậy x = 5dm

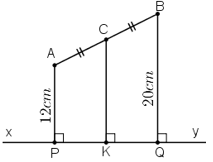
Bài 10 Hai điểm A và B thuộc cùng một nửa mặt phẳng có bờ là đường thẳng xy. Khoảng cách từ điểm A đến xy bằng 12cm, khoảng cách từ điểm B đến xy bằng 20cm. Tính khoảng cách từ trung điểm C của AB đến xy.

Lời giải:

Gọi P, Q, K lần lượt là chân đường vuông góc hạ từ A, B, C xuống xy.

+ AP ⊥ xy và BQ ⊥ xy ⇒ AP // BQ

⇒ Tứ giác ABQP là hình thang.

+ CK ⊥ xy ⇒ CK // AP//BQ

+ Hình thang ABQP có AC = CB (gt) và CK // AP // BQ

⇒ PK = KQ

⇒ CK là đường trung bình của hình thang

⇒ CK = $\frac{\left(AP+BQ\right)}{2}$.

Mà AP = 12cm, BQ = 20cm ⇒ CK = 16cm.

Vậy khoảng cách từ trung điểm C của AB đến xy bằng 16cm.

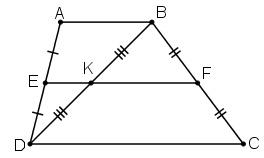
Bài 11 Hình thang ABCD có đáy AB, CD. Gọi E, F, K theo thứ tự là trung điểm của AD, BC, BD. Chứng minh ba điểm E, K, F thẳng hàng.

Lời giải:

+ ΔABD có DE = EA và DK = KB

⇒ EK là đường trung bình của ΔDAB

⇒ EK // AB

+ Hình thang ABCD có: AE = ED và BF = FC

⇒ EF là đường trung bình của hình thang ABCD

⇒ EF // AB// CD

+ Qua điểm E ta có EK // AB và EF // AB nên theo tiên đề Ơclit ta có E, K, F thẳng hàng.

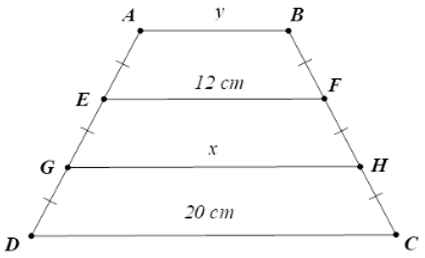
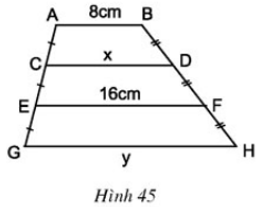
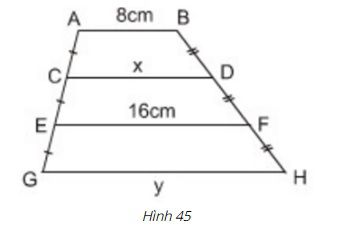
Bài 12 Tính x, y trên hình 45 trong đó AB // CD // EF // GH.

Hình 45

Lời giải:

+ Tính x :

AB // EF nên tứ giác ABFE là hình thang

Hình thang ABFE có: CA = CE và DB = DF

⇒ CD là đường trung bình của hình thang ABFE

⇒ CD = $\frac{\left(AB+EF\right)}{2}$

hay x = $\frac{\left(8+16\right)}{2}$ = 12(cm)

+ Tính y:

CD // GH nên tứ giác CDHG là hình thang

Hình thang CDHG có : EC = EG, FD = FH

⇒ EF là đường trung bình của hình thang CDHG

⇒ EF = $\frac{\left(CD+GH\right)}{2}$

hay $\frac{\left(x+y\right)}{2}$ = 16cm ⇒ x + y = 32cm

Mà x = 12cm ⇒ y = 20cm.

Vậy x = 12cm và y = 20cm.

Bài 14

Cho tứ giác ABCD. Gọi E, F, K theo thứ tự là trung điểm của AD, BC, AC.

a) So sánh các độ dài EK và CD, KF và AB

b) Chứng minh rằng

Lời giải:

a) + ΔADC có: AE = ED (gt) và AK = KC (gt)

⇒ EK là đường trung bình của ΔADC

⇒ EK = $\frac{CD}{2}$

+ ΔABC có AK = KC (gt) và BF = FC (gt)

⇒ KF là đường trung bình của ΔABC

⇒ KF = $\frac{AB}{2}$.

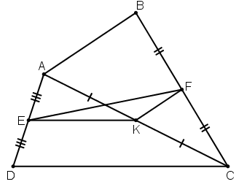
b) Ta có: EF ≤ EK + KF =

(Bổ sung: 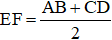⇔ EF = EK + KF ⇔ E, F, K thẳng hàng ⇔ AB // CD)

Bài 15 Cho hình thang ABCD (AB // CD), E là trung điểm của AD, F là trung điểm của BC. Đường thẳng EF cắt BD tại I, cắt AC ở K.

a) Chứng minh rằng AK = KC, BI = ID.

b) Cho AB = 6cm, CD = 10cm. Tính các độ dài EI, KF, IK.

Lời giải:

a) + Hình thang ABCD có EA = ED, FB = FC (gt)

⇒ EF là đường trung bình của hình thang ABCD.

⇒ EF // AB // CD

+ ΔABC có BF = FC (gt) và FK // AB (cmt)

⇒ AK = KC

+ ΔABD có: AE = ED (gt) và EI // AB (cmt)

⇒ BI = ID

b) + Vì EF là đường trung bình của hình thang ABCD.

⇒ EF = $\frac{\left(AB+CD\right)}{2}$ = $\frac{\left(6+10\right)}{2}$ = 8cm.

+ ΔABD có AE = ED, DI = IB

⇒ EI là đường trung bình của ΔABD

⇒ EI = $\frac{AB}{2}=\frac{6}{2}$ = 3(cm)

+ ΔABC có CF = BF, CK = AK

⇒ KF là đường trung bình của ΔABC

⇒ KF = $\frac{AB}{2}=\frac{6}{2}$ = 3cm

+ Lại có: EI + IK + KF = EF

⇒ IK = EF – EI – KF = 8 – 3 – 3 = 2cm

III. Bài tập vận dụng

Bài 1 Tính khoảng cách AB giữa hai mũi của compa trên hình 42, biết C là trung điểm của OA, D là trung điểm của OB và CD = 3cm.

Bài 2 Tìm x trên hình 44.

Bài 3 Cho hình 43. Chứng minh rằng AI = IM.

Bài 4 Hai điểm A và B thuộc cùng một nửa mặt phẳng có bờ là đường thẳng xy. Khoảng cách từ điểm A đến xy bằng 12cm, khoảng cách từ điểm B đến xy bằng 20cm. Tính khoảng cách từ trung điểm C của AB đến xy.

Cho tứ giác ABCD. Gọi E, F, K theo thứ tự là trung điểm của AD, BC, AC.

a) So sánh các độ dài EK và CD, KF và AB

b) Chứng minh rằng

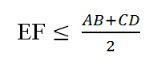
Bài 5 Tính x, y trên hình 45 trong đó AB // CD // EF // GH.

Bài 6 Cho hình thang ABCD (AB // CD), E là trung điểm của AD, F là trung điểm của BC. Đường thẳng EF cắt trung điểm của AD, F là trung điểm của BC. Đường thẳng EF cắt BD tại I, cắt AC ở K.

a) Chứng minh rằng AK = KC, BI = ID.

b) Cho AB = 6cm, CD = 10cm. Tính các độ dài EI, KF, IK.

Bài 7 Vẽ tam giác ABC bất kì rồi lấy trung điểm D của AB. Qua D vẽ đường thẳng song song với BC, đường thẳng này cắt AC ở E. Bằng quan sát, hãy nêu dự đoán về vị trí của điểm E trên cạnh AC.

Bài 8 Vẽ tam giác ABC bất kì rồi lấy trung điểm D của AB, trung điểm E của AC. Dùng thước đo góc và thước chia khoảng để kiểm tra rằng $\widehat{ADE}=\hat{B}$ và DE = $\frac{1}{2}$ BC.

Bài 9 Tính x trên hình 40.

Bài 10 Tính x, y trên hình.

Bài 11 Cho ABC kéo dài trung tuyến BD đến F sao cho DF = BD và trung tuyến CE đến G sao cho EG = CE. Chứng minh ba điểm G, A, F thẳng hàng.

Bài 12 Cho $\mathrm{\Delta }$ABC có $\hat{A}={50}^{\circ }$, $\hat{B}={70}^{\circ }$. Các điểm D, E lần lượt là trung điểm của AB, AC. Tứ giác BDEC là hình gì? Tính các góc của nó.

Bài 13 Cho $\mathrm{\Delta }$AKC cân tại A có đường cao AB. Kẻ BD $\perp$ AC, gọi E là trung điểm của BD. Chứng minh rằng $AE\perp$ KD

Bài 4 Cho hình thang cân ABCD có AB // CD; AB = 4cm; CD = 10cm; AD = 5cm. Lấy điểm E sao cho B là trung điểm của DE. Gọi H là chân đường cao kẻ từ E đến đường thẳng DC. Tính độ dài CH.

Bài 15 Cho $\mathrm{\Delta }$ABC, trung tuyến AM. Gọi D là một điểm trên cạnh AC sao cho AD = $\frac{1}{3}$AC, BD cắt AM tại I. Chứng minh AI = IM

Bài 16 Cho $\mathrm{\Delta }$ABC có AB = AC. Lấy điểm D trên cạnh AB, điểm E thuộc tia đối của tia CA sao cho BD = CE. Gọi I là giao điểm của DE với BC. Chứng minh DI = IE

Bài 17 Cho $\mathrm{\Delta }$ABC có trung tuyến AM. Qua O là trung điểm của trung tuyến AM kẻ đường thẳng d sao cho d cắt cả hai cạnh AB, AC. Gọi H, K, I lần lượt là chân các đường vuông góc kẻ từ các điểm A, B, C đến đường thẳng d. Chứng mỉnh rằng BK + CI = 2AH.

Bài 18 Tính x trên hình 41.

Bài 19 Cho $\mathrm{\Delta }$ABC có các đường trung tuyến BD, CE cắt nhau tại G. Gọi H, I lần lượt là trung điểm của GB, GC. Chứng minh DE // HI và DE = HI.

Bài 20. Chứng minh rằng trong một hình thang, trung điểm hai cạnh bên, trung điểm hai đường chéo là bốn điểm thẳng hàng.

Xem thêm các bài Bài tập Toán lớp 8 hay, chi tiết khác:

Bài tập Tứ giác

Bài tập Hình thang

Bài tập Hình thang cân

Bài tập Đối xứng trục

Bài tập Hình bình hành