Trắc nghiệm Phương trình đường tròn có đáp án – Toán lớp 10

Bộ 30 bài tập trắc nghiệm Toán 10 Bài 2: Phương trình đường tròn có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 10 Bài 2.

1 3,130 31/03/2022

Tải về

Trang trước

Trang sau

Trắc nghiệm Toán 10 Bài 2: Phương trình đường tròn

Bài giảng Trắc nghiệm Toán 10 Bài 2: Phương trình đường tròn

Câu 1. Tìm giao điểm $(C_{1}) : x^{2} + y^{2} - 2 = 0$ đường tròn và $(C_{2}) : x^{2} + y^{2} - 2 x = 0$

A. $(2; 0)$ và $(0; 2)$ .

B. $(\sqrt{2}; 1)$ và $(1; - \sqrt{2}) .$

C. $(1; - 1)$ và $(1; 1)$ .

D. $(- 1; 0)$ và $(0; - 1)$ .

Hiển thị đáp án

Đáp án: C

Giải thích:

Xét hệ:

$\{\begin{matrix} x^{2} + y^{2} - 2 = 0 \\ x^{2} + y^{2} - 2 x = 0 \end{matrix} \Leftrightarrow \{\begin{matrix} x = 1 \\ y^{2} = 1 \end{matrix} \Leftrightarrow \{\begin{matrix} x = 1 \\ [\begin{matrix} y = 1 \\ y = - 1 \end{matrix} \end{matrix}$

Vậy có hai giao điểm là: $(1; - 1)$ và $(1; 1)$

Câu 2. Đường tròn $x^{2} + y^{2} - 4 x - 2 y + 1 = 0$ tiếp xúc đường thẳng nào trong các đường thẳng dưới đây?

A. Trục tung.

B. $Δ_{1} : 4 x + 2 y - 1 = 0$ .

C. Trục hoành.

D. $Δ_{2} : 2 x + y - 4 = 0$ .

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có: $x^{2} + y^{2} - 4 x - 2 y + 1 = 0$

$\Leftrightarrow {(x - 2)}^{2} + {(y - 1)}^{2} = 4$ có tâm $I (2; 1)$ , bán kính R=2.

Vì $d (I, O y) = 2, d (I, O x) = 1,$

$d (I, Δ_{1}) = \frac{9}{2 \sqrt{5}}, d (I, Δ_{2}) = \frac{1}{\sqrt{5}}$ nên A đúng.

Câu 3. Với những giá trị nào của m thì đường thẳng $∆ : 3 x + 4 y + 3 = 0$ tiếp xúc với đường tròn (C) ${(x - m)}^{2} + y^{2} = 9$ :

A. m=0 và m=1.

B. m=4 và m=-6

C. m=2

D. m=6

Hiển thị đáp án

Đáp án: B

Giải thích:

Đường tròn có tâm I (m;0) và bán kính R=3.

Đường thẳng tiếp xúc với đường tròn khi và chỉ khi:

$d (I; △) = R = 3 \Leftrightarrow \frac{|3 m + 3|}{5} = 3 \Leftrightarrow [\begin{array}{l} m = 4 \\ m = - 6 \end{array}$

Câu 4. Cho đường tròn $(C) : x^{2} + y^{2} - 8 x + 6 y + 21 = 0$ và đường thẳng $d : x + y - 1 = 0$ . Xác định tọa độ các đỉnh A của hình vuông ABCD ngoại tiếp (C) biết $A \in d$

A. A(2;-1) hoặc A(6;-5).

B. A(2;-1) hoặc A(6;5).

C. A(2;1) hoặc A(6;-5).

D. A(2;1) hoặc A(6;5).

Hiển thị đáp án

Đáp án: A

Giải thích:

Đường tròn (C) có tâm I(4;-3), bán kính R=2

Tọa độ của I(4;-3) thỏa phương trình d: x + y -1 =0. Vậy $I \in d$ .

Vậy AI là một đường chéo của hình vuông ngoại tiếp đường tròn, có bán kính R=2, x=2 và x=6 là 2 tiếp tuyến của (C) nên

Hoặc là A là giao điểm các đường d và $x = 2 \Rightarrow A (2, - 1)$

Hoặc là A là giao điểm các đường (d) và $x = 6 \Rightarrow A (6, - 5)$ .

Câu 5. Cho tam giác ABC đều.Gọi D là điểm đối xứng của C qua AB.Vẽ đường tròn tâm D qua A,B ;M là điểm bất kì trên đường tròn đó $(M \neq A, M \neq B)$ . Khẳng định nào sau đây đúng?

A. Độ dài MA ,MB , MC là độ dài ba cạnh của một tam giác vuông.

B. MA ,MB , MC là ba cạnh của 1 tam giác vuông.

C. MA=MB=MC

D. MC > MB > MA

Hiển thị đáp án

Đáp án: A

Giải thích:

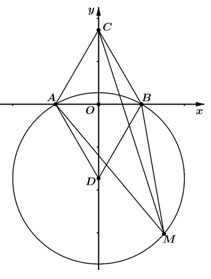
Chọn hệ trục Oxy sao cho Ox trùng với AB , chiều dương hướng từ A đến B,trục Oy là đường trung trực của đoạn AB $\Rightarrow A (- 1; 0), B (1; 0), C (0; \sqrt{3}), D (0; - \sqrt{3})$

Phương trình đường tròn tâm D qua A,B là: $x^{2} + {(y + \sqrt{3})}^{2} = 4 (1)$ .

Giả sử M(a,b) là điểm bất kì trên đường tròn (1).Ta có :

$M A^{2} = {(a + 1)}^{2} + b^{2}, M B^{2} = {(a - 1)}^{2} + b^{2}, M C^{2} = a^{2} + {(b - \sqrt{3})}^{2} . M A^{2} + M B^{2} = a^{2} + {(b - \sqrt{3})}^{2} + a^{2} + b^{2} + 2 b \sqrt{3} - 1 = M C^{2} + a^{2} + {(b + \sqrt{3})}^{2} - 4$

M nằm trên đường tròn (1) nên :

$a^{2} + {(b + \sqrt{3})}^{2} - 4 = 0 \Rightarrow M A^{2} + M B^{2} = M C^{2}$

$\Rightarrow M A$ , MB,MC là độ dài ba cạnh của một tam giác vuông.

Câu 6. Trong mặt phẳng với hệ tọa độ Oxy cho ba điểm A(0,a), B(b,0), C (-b,0) với a>0, b >0.Viết phương trình đường tròn (C) tiếp xúc với đường thẳng AB tại B và tiếp xúc với đường thẳngAC tại C.

A. $x^{2} + {(y - \frac{b^{2}}{a})}^{2} = b^{2} + \frac{b^{4}}{a^{2}}$ .

B. $x^{2} + {(y + \frac{b^{2}}{a})}^{2} = b^{2} + \frac{b^{4}}{a^{2}}$ .

C. $x^{2} + {(y + \frac{b^{2}}{a})}^{2} = b^{2} - \frac{b^{4}}{a^{2}}$ .

D. $x^{2} + {(y - \frac{b^{2}}{a})}^{2} = b^{2} - \frac{b^{4}}{a^{2}}$ .

Hiển thị đáp án

Đáp án: B

Giải thích:

$Δ A B C$ cân tại A;tâm I của (C) thuộc Oy $\Rightarrow I (0; y_{0})$

$\vec{I B} = (b; - y_{0}), \vec{A B} = (b; - a)$

Do $\vec{I B} . \vec{A B} = 0 \Rightarrow b^{2} + a y_{0} = 0$

$\Rightarrow y_{0} = - \frac{b^{2}}{a}$ .

Mặc khác $R^{2} = I B^{2} = b^{2} + y_{0}^{2}$

$= b^{2} + \frac{b^{4}}{a^{2}}$

Vậy phương trình của (C) là

$x^{2} + {(y + \frac{b^{2}}{a})}^{2} = b^{2} + \frac{b^{4}}{a^{2}}$

Câu 7. Trong mặt phẳng với hệ tọa độ Oxy cho đường tròn hai đường tròn $(C) : x^{2} + y^{2} - 2 x - 2 y + 1 = 0,$ $(C') : x^{2} + y^{2} + 4 x - 5 = 0$ cùng đi qua M(1;0). Viết phương trình đường thẳng d qua M cắt hai đường tròn $(C), (C')$ lần lượt tại A, B sao cho $M A = 2 M B$ .

A. $d : 6 x + y + 6 = 0$ hoặc $d : 6 x - y + 6 = 0$ .

B. $d : 6 x - y - 6 = 0$ hoặc $d : 6 x - y + 6 = 0$ .

C. $d : - 6 x + y - 6 = 0$ hoặc $d : 6 x - y - 6 = 0$ .

D. $d : 6 x + y - 6 = 0$ hoặc $d : 6 x - y - 6 = 0$ .

Hiển thị đáp án

Đáp án: D

Giải thích:

Gọi d là đường thẳng qua M có véc tơ chỉ phương

$\vec{u} = (a; b) \Rightarrow d : \{\begin{cases} x = 1 + a t \\ y = b t \end{cases}$

- Đường tròn : $(C_{1}) : I_{1} (1; 1), R_{1} = 1$

$(C_{2}) : I_{2} (- 2; 0), R_{2} = 3$

suy ra : $(C_{1}) : {(x - 1)}^{2} + {(y - 1)}^{2} = 1,$

$(C_{2}) : {(x + 2)}^{2} + y^{2} = 9$

Nếu d cắt $(C_{1})$ tại A:

$\Rightarrow (a^{2} + b^{2}) t^{2} - 2 b t = 0 \Leftrightarrow [\begin{array}{l} t = 0 \to M \\ t = \frac{2 b}{a^{2} + b^{2}} \end{array} \Rightarrow A (1 + \frac{2 a b}{a^{2} + b^{2}}; \frac{2 b^{2}}{a^{2} + b^{2}})$

Nếu d cắt $(C_{2})$ tại B:

$\Rightarrow (a^{2} + b^{2}) t^{2} + 6 a t = 0 \Leftrightarrow [\begin{array}{l} t = 0 \to M \\ t = - \frac{6 a}{a^{2} + b^{2}} \end{array} \Leftrightarrow B (1 - \frac{6 a^{2}}{a^{2} + b^{2}}; - \frac{6 a b}{a^{2} + b^{2}})$

- Theo giả thiết: $M A = 2 M B$

$\Leftrightarrow M A^{2} = 4 M B^{2} (*)$

- Ta có: ${(\frac{2 a b}{a^{2} + b^{2}})}^{2} + {(\frac{2 b^{2}}{a^{2} + b^{2}})}^{2}$

$= 4 [{(\frac{6 a^{2}}{a^{2} + b^{2}})}^{2} + {(\frac{6 a b}{a^{2} + b^{2}})}^{2}]$

$\Leftrightarrow \frac{4 b^{2}}{a^{2} + b^{2}} = 4. \frac{36 a^{2}}{a^{2} + b^{2}} \Leftrightarrow b^{2} = 36 a^{2} \Leftrightarrow [\begin{array}{l} b = - 6 a \to d : 6 x + y - 6 = 0 \\ b = 6 a \to d : 6 x - y - 6 = 0 \end{array}$

Câu 8. Tìm bán kính đường tròn đi qua 3 điểm $A (0; 4), B (3; 4), C (3; 0)$ .

A. 5.

B. 3.

C. $\frac{\sqrt{10}}{2}$ .

D. $\frac{5}{2}$ .

Hiển thị đáp án

Đáp án: D

Giải thích:

Gọi I(a,b) để I là tâm đường tròn đi qua ba điểm $A (0; 4), B (3; 4), C (3; 0)$ thì

$I A = I B = I C = R \Leftrightarrow \{\begin{cases} I A = I B \\ I A = I C \end{cases} \Leftrightarrow \{\begin{cases} a^{2} + {(4 - b)}^{2} = {(3 - a)}^{2} + {(4 - b)}^{2} \\ a^{2} + {(4 - b)}^{2} = {(3 - a)}^{2} + b^{2} \end{cases} \Leftrightarrow \{\begin{cases} a = \frac{3}{2} \\ b = 2 \end{cases}$

Vậy tâm I(1;1) , bán kính

$R = I A = \sqrt{{(\frac{3}{2})}^{2} + {(4 - 2)}^{2}} = \frac{5}{2}$

Câu 9. Phương trình nào sau đây không phải là phương trình đường tròn ?

A. $x^{2} + y^{2} - x + y + 4 = 0$

B. $x^{2} + y^{2} - y = 0$

C. $x^{2} + y^{2} - 2 = 0$ .

D. $x^{2} + y^{2} - 100 y + 1 = 0$ .

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có $x^{2} + y^{2} - x + y + 4 = 0$

$\Leftrightarrow {(x - \frac{1}{2})}^{2} + {(y + \frac{1}{2})}^{2} = - \frac{7}{2} < 0.$

Câu 10. Tìm tọa độ tâm đường tròn đi qua 3 điểm $A (0; 5), B (3; 4), C (- 4; 3)$ .

A. $(- 6; - 2)$ .

B. $(- 1; - 1)$ .

C. $(3; 1)$ .

D. $(0; 0)$ .

Hiển thị đáp án

Đáp án: D

Giải thích:

Gọi I(a,b)

Do I là tâm đường tròn đi qua ba điểm $A (0; 5), B (3; 4), C (- 4; 3)$ nên

$\{\begin{cases} I A = I B \\ I A = I C \end{cases} \Leftrightarrow \{\begin{cases} a^{2} + {(5 - b)}^{2} \\ = {(3 - a)}^{2} + {(4 - b)}^{2} \\ a^{2} + {(5 - b)}^{2} \\ = {(- 4 - a)}^{2} + {(3 - b)}^{2} \end{cases} \Leftrightarrow \{\begin{cases} 3 a + b = 0 \\ - 2 a + b = 0 \end{cases} \Leftrightarrow \{\begin{cases} a = 0 \\ b = 0 \end{cases}$

Vậy tâm I(0;0).

Câu 11. Đường tròn $x^{2} + y^{2} + 4 y = 0$ không tiếp xúc đường thẳng nào trong các đường thẳng dưới đây?

A. $x - 2 = 0$ .

B. $x + y - 3 = 0$ .

C. $x + 2 = 0$ .

D. Trục hoành.

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có đường tròn tâm I(0;-2) bán kính R=2

Dễ thấy đường tròn tiếp xúc với ba đường thẳng $x = 2; x = - 2; O x$

Câu 12. Đường tròn $x^{2} + y^{2} - 1 = 0$ tiếp xúc đường thẳng nào trong các đường thẳng dưới đây?

A. $x + y = 0$ .

B. $3 x + 4 y - 1 = 0$ .

C. $3 x - 4 y + 5 = 0$ .

D. $x + y - 1 = 0$ .

Hiển thị đáp án

Đáp án: D

Giải thích:

Đường tròn tâm I(0;0), bán kính R=1

Khoảng cách từ tâm đến các đường thẳng ở các đáp án là

$d_{A} = 0; d_{B} = \frac{1}{3} < R; d_{C} = \frac{5}{3} > R; d_{D} = 1 = R$

Vậy đáp án D là đường thẳng tiếp xúc với mặt cầu trên.

Câu 13. Tìm bán kính đường tròn đi qua 3 điểm $A (0; 0), B (0; 6), C (8; 0)$ .

A. 6.

B. 5.

C. 10.

D. $\sqrt{5}$ .

Hiển thị đáp án

Đáp án: B

Giải thích:

Gọi I(a;b) để I là tâm đường tròn đi qua ba điểm $A (0; 0), B (0; 6), C (8; 0)$ thì

$I A = I B = I C = R \Leftrightarrow \{\begin{cases} I A = I B \\ I A = I C \end{cases} \Leftrightarrow \{\begin{cases} a^{2} + b^{2} = a^{2} + {(6 - b)}^{2} \\ a^{2} + b^{2} = {(8 - a)}^{2} + b^{2} \end{cases} \Leftrightarrow \{\begin{cases} a = 4 \\ b = 3 \end{cases}$

Vậy tâm I(1;1),

bán kính $R = I A = \sqrt{4^{2} + 3^{2}} = 5$

Câu 14. Tìm giao điểm 2 đường tròn $(C_{2}) : x^{2} + y^{2} - 4 = 0$ và $(C_{2}) : x^{2} + y^{2} - 4 x - 4 y + 4 = 0$

A. $(\sqrt{2}; \sqrt{2})$ và $(\sqrt{2}; - \sqrt{2})$ .

B. $(0; 2)$ và $(0; - 2)$ .

C. $(2; 0)$ và $(0; 2)$ .

D. $(2; 0)$ và $(- 2; 0)$ .

Hiển thị đáp án

Đáp án: C

Giải thích:

Tọa độ giao điểm của hai đường tròn là nghiệm hệ phương trình

$\{\begin{cases} x^{2} + y^{2} - 4 = x^{2} + y^{2} - 4 x - 4 y + 4 \\ x^{2} + y^{2} - 4 = 0 \end{cases} \Leftrightarrow \{\begin{cases} x = 2 - y \\ {(2 - y)}^{2} + y^{2} - 4 = 0 \end{cases} \Leftrightarrow [\begin{array}{l} \{\begin{cases} x = 2 \\ y = 0 \end{cases} \\ \{\begin{cases} x = 0 \\ y = 2 \end{cases} \end{array}$

Câu 15. Đường tròn $x^{2} + y^{2} - 2 x + 10 y + 1 = 0$ đi qua điểm nào trong các điểm dưới đây ?

A. $(2; 1)$

B. $(3; - 2)$

C. $(- 1; 3)$

D. $(4; - 1)$

Hiển thị đáp án

Đáp án: D

Giải thích:

Thay lần lượt vào phương trình ta thấy tọa độ điểm ở đáp án D thỏa mãn.

Câu 16. Một đường tròn có tâm I(1;3) tiếp xúc với đường thẳng $∆ : 3 x + 4 y = 0$ . Hỏi bán kính đường tròn bằng bao nhiêu ?

A. $\frac{3}{5}$

B. 1

C. 3

D. 5

Hiển thị đáp án

Đáp án: C

Giải thích:

$R = d (I, Δ) = \frac{15}{5} = 3$

Câu 17. Đường tròn $(C) : {(x - 2)}^{2} {(y - 1)}^{2} = 25$ không cắt đường thẳng nào trong các đường thẳng sau đây?

A. Đường thẳng đi qua điểm (2;6) và điểm (45;50).

B. Đường thẳng có phương trình y-4=0.

C. Đường thẳng đi qua điểm (3;-2) và điểm (19;33).

D. Đường thẳng có phương trình x-8=0.

Hiển thị đáp án

Đáp án: D

Giải thích:

Tâm và bán kính đường tròn là $I (2; 1); R = 5$

Ta có đường thẳng đi qua hai điểm (2;6) và (45;50) là:

$\frac{x - 2}{43} = \frac{y - 6}{44} \Leftrightarrow 44 x - 43 y + 170 = 0$

Đường thẳng đi qua hai điểm (3;-2) và (19;33) là:

$\frac{x - 3}{16} = \frac{y + 2}{35} \Leftrightarrow 35 x - 16 y - 73 = 0$

Khoảng cách từ tâm đến các đường thẳng là

$d_{A} = \frac{215}{\sqrt{3785}} < R; d_{B} = 3 < R; d_{C} = \frac{19}{\sqrt{1481}} < R; d_{D} = 6 > R$

Câu 18. Đường tròn nào dưới đây đi qua 3 điểm $A (2; 0), B (0; 6), O (0; 0)$ ?

A. $x^{2} + y^{2} - 3 y - 8 = 0$ .

B. $x^{2} + y^{2} - 2 x - 6 y + 1 = 0$ .

C. $x^{2} + y^{2} - 2 x + 3 y = 0$ .

D. $x^{2} + y^{2} - 2 x - 6 y = 0$ .

Hiển thị đáp án

Đáp án: D

Giải thích:

Gọi phương trình cần tìm có dạng

$(C) : x^{2} + y^{2} + a x + b y + c = 0$ .

Do $A, B, O \in (C)$ nên ta có hệ

$\{\begin{cases} 2 a + c = - 4 \\ 6 b + c = - 36 \\ c = 0 \end{cases} \Leftrightarrow \{\begin{cases} a = - 2 \\ b = - 6 \\ c = 0 \end{cases}$

Vậy phương trình đường tròn là

$x^{2} + y^{2} - 2 x - 6 y = 0$ .

Câu 19. Đường tròn nào dưới đây đi qua điểm $A (4; - 2)$ .

A. $x^{2} + y^{2} - 2 x + 6 y = 0$ .

B. $x^{2} + y^{2} - 4 x + 7 y - 8 = 0$ .

C. $x^{2} + y^{2} - 6 x - 2 y + 9 = 0$ .

D. $x^{2} + y^{2} + 2 x - 20 = 0$ .

Hiển thị đáp án

Đáp án: A

Giải thích:

Thay tọa độ điểm $A (4; - 2)$ vào các đáp án ta được đáp án A thỏa mãn:

$4^{2} + {(- 2)}^{2} - 2.4 + 6. (- 2) = 0$

Câu 20. Xác định vị trí tương đối giữa 2 đường tròn $(C_{1}) : x^{2} + y^{2} = 4$ và $(C_{2}) : {(x + 10)}^{2} + {(y - 16)}^{2} = 1$ .

A. Cắt nhau.

B. Không cắt nhau.

C. Tiếp xúc ngoài.

D. Tiếp xúc trong.

Hiển thị đáp án

Đáp án: B

Giải thích:

Đường tròn $(C_{1})$ có tâm $I_{1} (0; 0)$ và bán kính $R_{1} = 2$ .

Đường tròn có tâm $I_{2} (- 10; 16)$ và bán kính $R_{2} = 1$ .

Câu 21. Ta có $I_{1} I_{2} = 2 \sqrt{89}$ và $R_{1} + R_{2} = 3$ . Do đó $I_{1} I_{2} > R_{1} + R_{2}$ nên 2 đường tròn không cắt nhau.

A. $m = - 3$

B. $m = 3$ và $m = - 3$ .

C. $m = 3$ .

D. $m = 15$ và $m = - 15$ .

Hiển thị đáp án

Đáp án: D

Giải thích:

Do đường tròn tiếp xúc với đường thẳng $∆$ nên

$R = d (I, Δ) = \frac{|4.0 + 3.0 + m|}{\sqrt{4^{2} + 3^{2}}} = 3 \Leftrightarrow m = \pm 15$

Câu 22. Đường tròn ${(x - a)}^{2} + {(y - b)}^{2} = R^{2}$ cắt đường thẳng $x + y - a - b = 0$ theo một dây cung có độ dài bằng bao nhiêu ?

A. $2 R$

B. $R \sqrt{2}$

C. $\frac{R \sqrt{2}}{2}$

D. $R$

Hiển thị đáp án

Đáp án: A

Giải thích:

$x + y - a - b = 0 \Leftrightarrow y = a + b - x$

thay vào ${(x - a)}^{2} + {(y - b)}^{2} = R^{2}$

ta có:

${(x - a)}^{2} + {(x - a)}^{2} = R^{2} \Leftrightarrow [\begin{array}{l} x = a + \frac{R}{\sqrt{2}} \\ \Rightarrow y = b - \frac{R}{\sqrt{2}} \\ x = a - \frac{R}{\sqrt{2}} \\ \Rightarrow y = b + \frac{R}{\sqrt{2}} \end{array}$

Vậy tọa độ giao điểm là:

$A (a + \frac{R}{\sqrt{2}}; b - \frac{R}{\sqrt{2}}); B (a - \frac{R}{\sqrt{2}}; b + \frac{R}{\sqrt{2}})$

$\vec{A B} = (- \frac{2 R}{\sqrt{2}}; \frac{2 R}{\sqrt{2}}) \Rightarrow A B = 2 R$

Câu 23. Tìm tọa độ giao điểm của đường thẳng $∆ : x - 2 y + 3 = 0$ và đường tròn $(C) : x^{2} + y^{2} - 2 x - 4 y = 0$ .

A. (3;3) và (-1;1).

B. (-1;1) và (3;-3)

C. (3;3) và (1;1)

D. Không có

Hiển thị đáp án

Đáp án: D

Giải thích:

$x - 2 y + 3 = 0 \Leftrightarrow x = 2 y - 3$

thay vào : $x^{2} + y^{2} - 2 x - 4 y = 0$

ta được:

${(2 y - 3)}^{2} + y^{2} - 2 (2 y - 3) - 4 y = 0 \Leftrightarrow 5 y^{2} - 16 y + 15 = 0 (V N)$

Câu 24. Xác định vị trí tương đối giữa 2 đường tròn: $x^{2} + y^{2} - 4 x = 0$ và $(C_{2}) x^{2} + y^{2} + 8 y = 0$

A. Tiếp xúc trong.

B. Không cắt nhau.

C. Cắt nhau.

D. Tiếp xúc ngoài.

Hiển thị đáp án

Đáp án: C

Giải thích:

$(C_{1})$ có bán kính $R_{1} = 2$ ; $(C_{2})$ có bán kính $R_{2} = 4$

Xét hệ $\{\begin{cases} x^{2} + y^{2} - 4 x = 0 \\ x^{2} + y^{2} + 8 y = 0 \end{cases}$

$\Leftrightarrow \{\begin{cases} x^{2} + y^{2} - 4 x = 0 \\ x = - 2 y \end{cases} \Leftrightarrow \{\begin{cases} 5 y^{2} + 8 y = 0 \\ x = - 2 y \end{cases}$

Câu 25. Tìm tọa độ giao điểm của đường thẳng $Δ : x + y - 7 = 0$ và đường tròn $(C) : x^{2} + y^{2} - 25 = 0$ .

A. (3;4) và (-4;3).

B. (4;3).

C. (3;4).

D. (3;4) và (4;3).

Hiển thị đáp án

Đáp án: D

Giải thích:

$Δ : x + y - 7 = 0 \Leftrightarrow y = 7 - x$

thay vào phương trình (C) ta được:

$x^{2} + {(7 - x)}^{2} - 25 = 0 \Leftrightarrow x^{2} - 7 x + 12 = 0 \Leftrightarrow [\begin{matrix} x = 3 \Rightarrow y = 4 \\ x = 4 \Rightarrow y = 3 \end{matrix} .$

Vậy tọa độ giao điểm là (3;4) và (4;3).

Câu 26. Đường tròn $x^{2} + y^{2} - 2 x - 2 y - 23 = 0$ cắt đường thẳng $Δ : x - y + 2 = 0$ theo một dây cung có độ dài bằng bao nhiêu ?

A. 5.

B. $2 \sqrt{23} .$

C. 10

D. $5 \sqrt{2} .$

Hiển thị đáp án

Đáp án: B

Giải thích:

$x^{2} + y^{2} - 2 x - 2 y - 23 = 0 \Leftrightarrow {(x - 1)}^{2} + {(y - 1)}^{2} = 25$

có tâm I(1;1) và bán kính R=5

Gọi $d (I, Δ) = \frac{|1 - 1 + 2|}{\sqrt{2}} = \sqrt{2} < R$

suy ra đường thẳng $∆$ cắt đường tròn theo dây cung AB và $A B = 2 \sqrt{R^{2} - d^{2}} = 2 \sqrt{23} .$

Câu 27. Đường tròn nào sau đây tiếp xúc với trục Oy?

A. $x^{2} + y^{2} - 10 x + 2 y + 1 = 0$ .

B. $x^{2} + y^{2} - 4 y - 5 = 0$ .

C. $x^{2} + y^{2} - 1 = 0.$

D. $x^{2} + y^{2} + x + y - 3 = 0$ .

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có:

$x^{2} + y^{2} - 10 x + 2 y + 1 = 0 \Leftrightarrow {(x - 5)}^{2} + {(y + 1)}^{2} = 25$

có tâm $I_{1} (5; - 1)$ và bán kính R=5.

Vì $d (I_{1}; O y) = 5 = R$ nên A đúng.

Câu 28. Tìm giao điểm 2 đường tròn $x^{2} + y^{2} = 5$ và $C_{2} : x^{2} + y^{2} - 4 x - 8 y + 15 = 0$

A. $(1; 2)$ và $(\sqrt{2}; \sqrt{3})$ .

B. $(1; 2)$ .

C. $(1; 2)$ và $(\sqrt{3}; \sqrt{2})$ .

D. $(1; 2)$ và $(2; 1)$ .

Hiển thị đáp án

Đáp án: B

Giải thích:

Tọa độ giao điểm của hai đường tròn là nghiệm hệ phương trình:

$\{\begin{cases} x^{2} + y^{2} - 5 \\ = x^{2} + y^{2} - 4 x - 8 y + 15 \\ x^{2} + y^{2} - 5 = 0 \end{cases} \Leftrightarrow \{\begin{cases} x = 5 - 2 y \\ {(5 - 2 y)}^{2} + y^{2} - 5 = 0 \end{cases} \Leftrightarrow [\{\begin{cases} x = 1 \\ y = 2 \end{cases}$

Câu 29. Đường tròn nào sau đây tiếp xúc với trục Ox?

A. $x^{2} + y^{2} - 2 x - 10 y = 0$ .

B. $x^{2} + y^{2} + 6 x + 5 y + 9 = 0$ .

C. $x^{2} + y^{2} - 10 y + 1 = 0$ .

D. $x^{2} + y^{2} - 5 = 0$ .

Hiển thị đáp án

Đáp án: B

Giải thích:

Do đường tròn tiếp xúc với trục Ox nên

$R = d (I, O x) = |y_{I}|$ .

Phương trình trục Ox là y=0.

Đáp án A sai vì: Tâm $I (1; 5)$ và bán kính $R = \sqrt{26}$ . Ta có

$d (I, O x) = |y_{I}| \neq R$ .

Đáp án B đúng vì: Tâm $I (- 3; - \frac{5}{2})$ và bán kính $R = \frac{5}{2}$ . Ta có

$d (I, O x) = |y_{I}| = R$ .

Đáp án C sai vì: Tâm $I (0; 5)$ và bán kính $R = \sqrt{24}$ . Ta có

$d (I, O x) = |y_{I}| \neq R$ .

Đáp án D sai vì: Tâm $I (0; 0)$ và bán kính $R = \sqrt{5}$ . Ta có

$d (I, O x) = |y_{I}| \neq R$ .

Câu 30. Đường tròn nào sau đây tiếp xúc với trục Oy?

A. $x^{2} + y^{2} - 10 y + 1 = 0$

B. $x^{2} + y^{2} + 6 x + 5 y - 1 = 0$

C. $x^{2} + y^{2} - 2 x = 0$ .

D. $x^{2} + y^{2} - 5 = 0$ .

Hiển thị đáp án

Đáp án: C

Giải thích:

Do đường tròn tiếp xúc với trục Oy nên $R = d (I, O y) = |x_{I}|$ .

Phương trình trục Oy là x=0.

Đáp án A sai vì: Tâm I(0;5) và bán kính $R = \sqrt{24}$ . Ta có

$d (I, O y) = |x_{I}| \neq R$ .

Đáp án B sai vì: Tâm $I (- 3; - \frac{5}{2})$ và bán kính $R = \frac{\sqrt{65}}{2}$ . Ta có

$d (I, O y) = |x_{I}| \neq R$ .

Đáp án C đúng vì: Tâm $I (1; 0)$ và bán kính $R = 1$ . Ta có

$d (I, O y) = |x_{I}| = R$ .

Đáp án D sai vì: Tâm $I (0; 0)$ và bán kính $R = \sqrt{5}$ . Ta có

$d (I, O y) = |x_{I}| \neq R$ .

Các câu hỏi trắc nghiệm Toán lớp 10 có đáp án, chọn lọc khác:

Trắc nghiệm Các hệ thức lượng trong tam giác và giải tam giác có đáp án

Trắc nghiệm ôn tập chương 2 có đáp án

Trắc nghiệm Phương trình đường thẳng có đáp án

Trắc nghiệm Phương trình elip có đáp án

Trắc nghiệm ôn tập chương 3 có đáp án

1 3,130 31/03/2022

Tải về

Trang trước

Trang sau

Xem thêm các chương trình khác:

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 3 lên lớp 4

Lớp 3 - Sách cũ

Tiếng Anh 3