Trắc nghiệm Bài ôn tập chương 1. Vecto có đáp án – Toán lớp 10
Bộ 29 bài tập trắc nghiệm Toán 10 Bài ôn tập chương 1. Vecto có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 10 Bài Ôn tập chương 1.
Trắc nghiệm Toán 10 Bài: ôn tập chương 1. Vecto
Câu 1. Cho tứ giác ABCD có →AB=→DC và |→AB|=|→BC|. Khẳng định nào sau đây sai?
A. →AD=→BC .
B. ABCD là hình thoi.
C. |→CD|=|→BC| .
D. ABCD là hình thang cân.
Đáp án: D
Giải thích:
Tứ giác ABCD có →AB=→DC⇒ABCD là hình bình hành (1) , nên →AD=→BC.
Mà|→AB|=|→BC|(2).
Từ (1) và (2) ta có ABCD là hình thoi nên |→CD|=|→BC|.
Câu 2. Trong mặt phẳng toạ độ Oxy, cho ba điểm A(−2;5),B(2;2) , C(10;−5). Tìm điểm E(m;1) sao cho tứ giác ABCE là hình thang có một đáy là CE.
A. E(−2;1).
B. E(0;1) .
C. E(2;1) .
D. E(−1;1).
Đáp án: C
Giải thích:
Ta có →BA=(−4;3),→BC=(8;−7)⇒→BA, →BC không cùng phương nên A, B, C không thẳng hàng,→CE=(m−10;6) . Để ABCE là hình thang có một đáy là CE thì →CE cùng chiều với →BA⇒m−10−4=63>0⇔m=2 .
Vậy E(2;1).
Câu 3. Cho hình vuông ABCD tâm O cạnh a. Biết rằng tập hợp các điểm M thỏa mãn 2MA2+MB2+2MC2+MD2=9a2 là một đường tròn. Bán kính của đường tròn đó là
A. R=2a.
B. R=3a.
C. R=a.
D. R=a√2.
Đáp án: C
Giải thích:
2MA2+MB2+2MC2+MD2=9a2
⇔2(→MO+→OA)2+(→MO+→OB)2+2(→MO+→OC)2+(→MO+→OD)2=9a2
⇔6MO2+2OA2+OB2+2OC2+OD2+2→MO(2→OA+2→OC+→OB+→OD)⏟→0=9a2
⇔6MO+23a2=9a2⇔MO=a
Vậy tập hợp các điểm M là đường tròn tâm O bán kính R=a.
Câu 4. Cho hình chữ nhật ABCD tâm O. Gọi M , N lần lượt là trung điểm của OA và CD. Biết →MN=a.→AB+b.→AD. Tính a+b.
A. a+b=1 .
B. a+b=12 .
C. a+b=34 .
D. a+b=14 .
Đáp án: A
Giải thích:
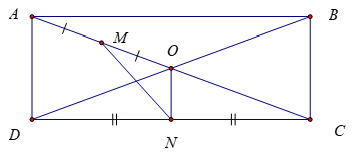
→MN=→MO+→ON=14→AC+12→AD
=14(→AB+→BC)+12→AD
=14(→AB+→AD)+12→AD
=14→AB+34→AD
⇒a=14;b=34 .
Vậy a+b=1.
Câu 5. Véctơ có điểm đầu là A , điểm cuối là B được kí hiệu là
A. AB .
B. |→AB|.
C. →BA.
D. →AB .
Đáp án: D
Câu 6. Trong mặt phẳng tọa độ Oxy, cho hai điểm A(−4; 0) và B(0; 3). Xác định tọa độ của vectơ →u=2→AB
A. →u=(−8; −6) .
B. →u=(8; 6) .
C. →u=(−4; −3) .
D. →u=(4; 3) .
Đáp án: B
Giải thích:
→AB=(4; 3)⇒→u=2→AB=(8; 6).
Câu 7. Trong mặt phẳng tọa độ Oxy, cho A(3; −1), B(−1; 2) và I(1; −1). Tìm tọa độ điểm C để I là trọng tâm tam giác ABC.
A. C(1; −4) .
B. C(1; 0).
C. C(1; 4) .
D. C(9; −4) .
Đáp án: A
Giải thích:
Điểm I là trọng tâm tam giác ABC
⇔{xI=xA+xB+xC3yI=yA+yB+yC3
⇔{xC=3xI−xA−xByC=3yI−yA−yB
⇔{xC=3−3−(−1)=1yC=−3−(−1)−2=−4
Vậy điểm C(1; −4).
Câu 8. Xét các mệnh đề sau
(I): Véc tơ – không là véc tơ có độ dài bằng 0.
(II): Véc tơ – không là véc tơ có nhiều phương.
A. Chỉ (I) đúng.
B. Chỉ (II) đúng.
C. (I) và (II) đúng.
D. (I) và (II) sai.
Đáp án: C
Giải thích:
Véc tơ – không là véc tơ có điểm đầu, điểm cuối trùng nhau nên có độ dài bằng 0.
Véc tơ – không cùng phương với mọi véc tơ.
Câu 9. Cho hình vuông ABCD có cạnh bằng a. Độ dài |→AD+→AB| bằng
A. 2a
B. a√22 .
C. a√32 .
D. a√2 .
Đáp án: D
Giải thích:
Theo quy tắc đường chéo hình bình hành, ta có:
|→AD+→AB|=|→AC|=AC
=AB√2=a√2.
Câu 10. Trong mặt phẳng với hệ tọa độ Oxy, cho hai điểm A(2;−5) và B(4;1). Tọa độ trung điểm I của đoạn thẳng AB là
A. I(1;3) .
B. I(−1;−3) .
C. I(3;2) .
D. I(3;−2).
Đáp án: D
Giải thích:
Tọa độ trung điểm I của đoạn thẳng: AB
{xI=xA+xB2yI=yA+yB2
⇒{xI=3yI=−2⇒I(3;−2).
Câu 11. Cho tam giác ABC với A(−2;3), B(4;−1), trọng tâm của tam giác là G(2;−1). Tọa độ đỉnh C là
A. (6; −4) .
B. (6; −3) .
C. (4; −5) .
D. (2; 1) .
Đáp án: C
Giải thích:
Do G là trọng tâm tam giác ABC nên
{xG=xA+xB+xC3yG=yA+yB+yC3
⇔{xC=3xG−xA−xByC=3yG−yA−yB⇔{xC=4yC=−5
Vậy C(4; −5).
Câu 12. Cho các điểm A, B,C , D và số thực k. Mệnh đề nào sau đây đúng?
A. AB=|k|CD⇒→AB =k→CD .
B. AB=kCD⇒→AB =k→CD .
C. →AB =k→CD ⇒AB=|k|CD .
D. →AB =k→CD ⇒AB=kCD .
Đáp án: C
Giải thích:
Theo định nghĩa phép nhân véc tơ với một số.
Câu 13. Trong mặt phẳng với hệ tọa độ Ox cho các điểm A(1; 2), B(3; −1), C(0; 1). Tọa độ của véctơ →u=2→AB+→BC là
A. →u=(2; 2) .
B. →u=(−4; 1) .
C. →u=(1; −4) .
D. →u=(−1; 4) .
Đáp án: C
Giải thích:
Ta có:
→AB=(2; −3)⇒2→AB=(4; −6)
→BC=(−3; 2)
Nên →u=2→AB+→BC=(1; −4).
Câu 14. Mệnh đề nào sau đây sai?
A. G là trọng tâm ΔABC thì →GA+→GB+→GC=→0 .
B. Ba điểm A, B, C bất kì thì →AC=→AB+→BC.
C. I là trung điểm AB thì →MI=→MA+→MB với mọi điểm M.
D. ABCD là hình bình hành thì →AC=→AB+→AD.
Đáp án: C
Giải thích:
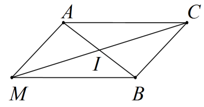
Với mọi điểm M, ta dựng hình bình hành AMBC.
Khi đó, theo quy tắc hình bình hành:
→MA+→MB=→MC=2→MI .
Câu 15. Cho ΔABC có trọng tâm G. Khẳng định nào sau đây đúng?
A. →AG =→AB +→AC .
B. →AG =2(→AB +→AC ).
C. →AG =13(→AB +→AC ) .
D. →AG =23(→AB +→AC ) .
Đáp án: C
Giải thích:
Gọi M là trung điểm BC, ta có:
→AG=23→AM
=23.12(→AB+→AC)
=13(→AB+→AC).
Câu 16. Cho tam giác ABC. Gọi I, J là hai điểm xác định bởi →IA=2→IB, 3→JA+2→JC=→0. Hệ thức nào đúng?
A. →IJ=52→AC−2→AB .
B. →IJ=52→AB−2→AC.
C. →IJ=25→AB−2→AC.
D. →IJ=25→AC−2→AB .
Đáp án: D
Giải thích:
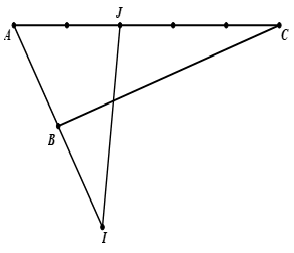
Ta có:
→IJ=→IA+→AJ
=−2→AB+25→AC
=25→AC−2→AB
Câu 17. Trong mặt phẳng Oxy, cho hình bình hành ABCD có A(2;−3), B(4;5) và G(0;−133) là trọng tâm tam giác ADC. Tọa độ đỉnh D là
A. D(2;1) .
B. D(−1;2) .
C. D(−2;−9) .
D. D(2;9) .
Đáp án: C
Giải thích:
Cách 1: Gọi D(a; b). Vì G(0;−133) là trọng tâm tam giác ADC nên
→BD=32→BG
⇔{a−4=32(0−4)b−5=32(−133−5)⇔{a=−2b=−9
⇒D(−2; −9)
Cách 2: Gọi I là trọng tâm tam giác ABC suy ra I là trung điểm BG ⇒I(2; 13).
Lại có G(0;−133) là trung điểm DI nên suy ra D(−2; −9).
Câu 18. Hai vectơ có cùng độ dài và ngược hướng gọi là
A. Hai vectơ cùng hướng.
B. Hai vectơ cùng phương.
C. Hai vectơ đối nhau.
D. Hai vectơ bằng nhau.
Đáp án: C
Giải thích:
Hai vectơ đối nhau là hai vectơ có cùng độ dài và ngược hướng.
Câu 19. Cho ba điểm M,N , P thẳng hàng, trong đó điểm N nằm giữa hai điểm M và P. Khi đó các cặp vectơ nào sau đây cùng hướng?
A. →MP và →PN.
B. →MN và →PN.
C. →NM và →NP.
D. →MN và →MP.
Đáp án: D
Giải thích:
![]()
Ta thấy →MN và →MP cùng hướng.
Câu 20. Cho tam giác ABC. Điểm M thỏa mãn →AB+→AC=2→AM. Chọn khẳng định đúng.
A. M là trọng tâm tam giác.
B. M là trung điểm của BC.
C. M trùng với B hoặc C.
D. M trùng với A.
Đáp án: B
Giải thích:
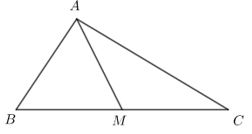
Ta có →AB+→AC=2→AM
⇒M là trung điểm của BC
Câu 21. Tổng →MN+→PQ+→RN+→NP+→QR bằng
A. →MR .
B. →MN .
C. →MP .
D. →MQ .
Đáp án: B
Giải thích:
Ta có:
→MN+→PQ+→RN+→NP+→QR=→MN+(→PQ+→QR+→RN+→NP)=→MN+→0=→MN.
Câu 22. Cho 4 điểm bất kì A,B ,C ,D . Đẳng thức nào sau đây đúng?
A. →OA=→OB−→BA .
B. →OA=→CA−→CO .
C. →AB=→AC+→BC .
D. →AB=→OB+→OA .
Đáp án: B
Giải thích:
→OA=→OB−→BA⇔→OA−→OB
=−→BA⇔→BA=−→BA nên A sai
→OA=→CA−→CO⇔→OA−→CA
=−→CO⇔→OA+→AC=−→CO⇔→OC=−→CO
nên B đúng.
Câu 23. Trong mặt phẳng tọa độ Oxy, cho hai điểm A(1;0) và B(0;−2). Tọa độ trung điểm của đoạn thẳng AB là
A. (12;−1) .
B. (−1;12) .
C. (12;−2) .
D. (1;−1) .
Đáp án: A
Giải thích:
Tọa độ trung điểm của đoạn thẳng AB là I(1+02; 0−22) hay I(12;−1).
Câu 24. Trong mặt phẳng tọa độ Oxy, cho B(2; 3),C(−1; −2) . Điểm M thỏa mãn 2→MB+3→MC=→0. Tọa độ điểm M là
A. M(15; 0) .
B. M(−15; 0) .
C. M(0; 15) .
D. M(0; −15).
Đáp án: A
Giải thích:
Gọi M(x; y)
⇒{→MB=(2−x; 3−y)→MC=(−1−x; −2−y)
⇒2→MB+3→MC=(−5x+1;−5y)
Khi đó 2→MB+3→MC=→0.
⇔{−5x+1=0−5y=0⇔{x=15y=0
Vậy M(15; 0).
Câu 25. Trong mặt phẳng tọa độ Oxy, cho các vectơ →u=(2;−4),→a=(−1;−2) , →b=(1;−3). Biết →u=m→a+n→b, tính m−n.
A. 5.
B. -2.
C. -5.
D. 2.
Đáp án: B
Giải thích:
Ta có:
→u=m→a+n→b
⇔{−m+n=2−2m−3n=−4
⇔{m=−25n=85.
Suy ra m−n=−2
Câu 26. Cho tam giác ABC có G là trọng tâm, I là trung điểm BC. Tìm khẳng định sai.
A. |→IB+→IC+→IA|=IA .
B. |→IB+→IC|=BC .
C. |→AB+→AC|=2AI .
D. |→AB+→AC|=3GA .
Đáp án: B
Giải thích:
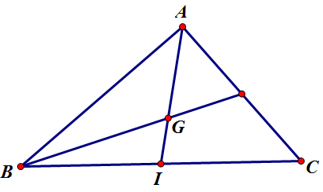
|→IB+→IC+→IA|=|→0+→IA|=|→IA|=IA (Do I là trung điểm BC) nên khẳng định ở A đúng.
|→AB+→AC|=|2→AI|=2AI (Do I là trung điểm BC) nên khẳng định ở C đúng.
|→AB+→AC|=2AI=3GA (Do G là trọng tâm tam giác ABC) nên khẳng định ở D đúng.
|→IB+→IC|=|→0|=0 (Do I là trung điểm BC) nên khẳng định ở B sai.
Câu 27. Cho hình bình hành ABCD có N là trung điểm AB và G là trọng tâm ΔABC. Phân tích →GA theo →BD và →NC
A. →GA=−13→BD+23→NC.
B. →GA=13→BD−43→NC.
C. →GA=13→BD+23→NC.
D. →GA=13→BD−23→NC.
Đáp án: D
Giải thích:
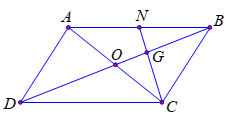
Vì G là trọng tâm ΔABC nên
→GA+→GB+→GC=→0⇔→GA=−(→GB+→GC)
Suy ra →GA=−(−13→BD+23→NC)
=13→BD−23→NC.
Câu 28. Trong mặt phẳng tọa độ Oxy, cho các vectơ →u =(−2 ; 1) và →v =3→i −m→j . Tìm m để hai vectơ →u , →v cùng phương.
A. −23.
B. 23 .
C. −32.
D. 32 .
Đáp án: D
Giải thích:
Ta có →v =3→i −m→j
⇒→v =(3 ; −m).
Hai vectơ →u ,→v cùng phương
⇔3−2=−m1⇔m=32.
Câu 29. Cho →a=(2; 1),→b=(−3; 4) ,→c=(−4; 9) . Hai số thực m,n thỏa mãn m→a+n→b=→c. Tính m2+n2.
A. 5.
B. 3.
C. 4.
D. 1.
Đáp án: A
Giải thích:
Ta có:
m→a+n→b=→c ⇔ {2m−3n=−4m+4n=9 ⇔ {m=1n=2 .
Câu 30. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có M(−52;−1),N(−32;−72), P(0;12) lần lượt là trung điểm các cạnh BC,CA , AB. Tọa độ trọng tâm G của tam giác ABC là
A. G(−43;−43) .
B. G(−4;−4) .
C. G(43;43) .
D. G(4;−4) .
Đáp án: A
Giải thích:
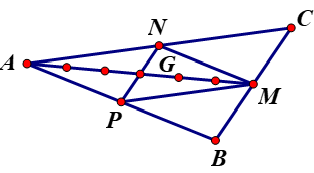
Vì G là trọng tâm tam giác ABC nên G cũng là trọng tâm tam giác MNP.
Tọa độ điểm G là
{xG=xM+xN+xP3yG=yM+yN+yP3
⇔{xG=−43yG=−43
Các câu hỏi trắc nghiệm Toán lớp 10 có đáp án, chọn lọc khác:
Trắc nghiệm Giá trị lượng giác của một góc bất kì từ 0 độ đến 180 độ có đáp án
Trắc nghiệm Tích vô hướng của hai vecto có đáp án
Trắc nghiệm Các hệ thức lượng trong tam giác và giải tam giác có đáp án
Xem thêm các chương trình khác:
- Trắc nghiệm Sinh học lớp 7 có đáp án
- Trắc nghiệm Toán lớp 7 có đáp án
- Trắc nghiệm Ngữ văn lớp 7 có đáp án
- Trắc nghiệm Sinh học 8 có đáp án
- Trắc nghiệm Toán lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn 8 có đáp án
- Trắc nghiệm Hóa học lớp 8 có đáp án
- Trắc nghiệm Địa Lí lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Tiếng Anh lớp 8 có đáp án
- Trắc nghiệm GDCD lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Lịch sử lớp 8 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Vật Lí lớp 8 có đáp án
- Trắc nghiệm Công nghệ lớp 8 có đáp án
- Trắc nghiệm Tin học lớp 8 có đáp án
- Trắc nghiệm Sinh học lớp 9 có đáp án
- Trắc nghiệm Toán lớp 9 có đáp án
- Trắc nghiệm Ngữ văn 9 có đáp án
- Trắc nghiệm Hóa học lớp 9 có đáp án
- Trắc nghiệm Địa lí lớp 9 có đáp án
- Trắc nghiệm Tiếng Anh lớp 9 có đáp án
- Trắc nghiệm GDCD lớp 9 có đáp án
- Trắc nghiệm Lịch sử lớp 9 có đáp án
- Trắc nghiệm Vật lí lớp 9 có đáp án
- Trắc nghiệm Công nghệ lớp 9 có đáp án
- Trắc nghiệm Sinh học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Toán lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Hóa học lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Ngữ văn lớp 11 có đáp án
- Trắc nghiệm Tiếng Anh lớp 11 có đáp án
- Trắc nghiệm Vật Lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Địa lí lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm GDCD lớp 11 có đáp án
- Trắc nghiệm Lịch sử lớp 11 có đáp án (Sách mới) | Kết nối tri thức, Cánh diều, Chân trời sáng tạo
- Trắc nghiệm Công nghệ lớp 11 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 11 có đáp án
- Trắc nghiệm Tin học lớp 11 có đáp án
- Trắc nghiệm Toán lớp 12 có đáp án
- Trắc nghiệm Sinh học lớp 12 có đáp án
- Trắc nghiệm Hóa học lớp 12 có đáp án
- Trắc nghiệm Ngữ văn lớp 12 có đáp án
- Trắc nghiệm Tiếng Anh lớp 12 có đáp án
- Trắc nghiệm Địa lí lớp 12 có đáp án
- Trắc nghiệm Vật Lí lớp 12 có đáp án
- Trắc nghiệm Công nghệ lớp 12 có đáp án
- Trắc nghiệm Giáo dục công dân lớp 12 có đáp án
- Trắc nghiệm Lịch sử lớp 12 có đáp án
- Trắc nghiệm Giáo dục quốc phòng - an ninh lớp 12 có đáp án
