Trắc nghiệm Ôn tập chương 3 có đáp án – Toán lớp 10

Bộ 28 bài tập trắc nghiệm Toán lớp 10 Bài ôn tập chương 3 có đáp án đầy đủ các mức độ giúp các em ôn trắc nghiệm Toán 10 Bài Ôn tập chương 3.

1 890 31/03/2022

Tải về

Trang trước

Trang sau

Trắc nghiệm Toán 10 Bài: ôn tập chương 3

Câu 1. Với giá trị nào của a thì phương trình: $3 |x| + 2 a x = - 1$ có nghiệm duy nhất:

A. $a > \frac{3}{2}$ .

B. $a < \frac{- 3}{2}$ .

C. $a \neq \{\frac{- 3}{2}; \frac{3}{2}\}$ .

D. $a < \frac{- 3}{2} \lor a > \frac{3}{2}$ .

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có: $3 |x| + 2 a x = - 1$

$\Leftrightarrow 3 |x| = - 1 - 2 a x$

$\Leftrightarrow - 1 - 2 a x \geq 0 \cap [\begin{array}{l} 3 x = - 1 - 2 a x \\ 3 x = 1 + 2 a x \end{array}$

$\Leftrightarrow 2 a x \leq - 1 \cap [\begin{array}{l} (3 + 2 a) x = - 1 (2) \\ (3 - 2 a) x = 1 (3) \end{array}$

Giải hệ này ta được

$\Leftrightarrow [\begin{array}{l} a < \frac{- 3}{2} \\ a > \frac{3}{2} \end{array}$

Vậy phương trình (1) có nghiệm duy nhất

$\Leftrightarrow [\begin{array}{l} a < \frac{- 3}{2} \\ a > \frac{3}{2} \end{array}$ .

Câu 2. Phương trình: $|x| + 1 = x^{2} + m$ có 1 nghiệm duy nhất khi và chỉ khi :

A. m=0

B. m=1

C. m=-1

D. Không tồn tại giá trị m thỏa.

Hiển thị đáp án

Đáp án: D

Giải thích:

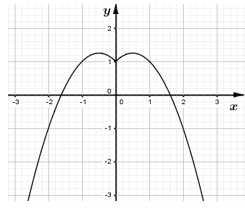
$|x| + 1 = x^{2} + m$

$\Leftrightarrow m = f (x) = \{\begin{cases} - x^{2} + x + 1 k h i x \geq 0 \\ - x^{2} - x + 1 k h i x < 0 \end{cases}$

Biểu diễn đồ thị hàm số $f (x)$ lên hệ trục tọa độ như hình vẽ bên trên. Dựa vào đồ thị ta suy ra không tồn tại m để phương trình $m = f (x)$ có duy nhất 1 nghiệm.

Câu 3. Tập nghiệm của phương trình là $\frac{x^{2} - 4 x - 2}{\sqrt{x - 2}} = \sqrt{x - 2}$ :

A. $S = \{2\}$ .

B. $S = \{1\}$ .

C. $S = \{0; 1\}$ .

D. $S = \{5\}$ .

Hiển thị đáp án

Đáp án: C

Giải thích:

Điều kiện: $x > 2$

Ta có $\frac{x^{2} - 4 x - 2}{\sqrt{x - 2}} = \sqrt{x - 2}$

$\Leftrightarrow x^{2} - 4 x - 2 = x - 2$

$\Leftrightarrow x^{2} - 5 x = 0 \Leftrightarrow [\begin{array}{l} x = 0 (l) \\ x = 5 (n) \end{array}$

Vậy $S = \{5\}$ .

Câu 4. Số nghiệm của phương trình: $\sqrt{x - 4} (x^{2} - 3 x + 2) = 0$ là:

A. 0 .

B. 1 .

C. 2.

D. 3.

Hiển thị đáp án

Đáp án: B

Giải thích:

Điều kiện: $x \geq 4$

Phương trình thành :

$\sqrt{x - 4} (x^{2} - 3 x + 2) = 0$

$\Leftrightarrow [\begin{array}{l} x = 4 (n) \\ x = 1 (l) \\ x = 2 (l) \end{array} \Leftrightarrow x = 4$

Câu 5. Phương trình $(x^{2} - 3 x + m) (x - 1) = 0$ có 3 nghiệm phân biệt khi :

A. $m < \frac{9}{4}$ .

B. $m \leq \frac{9}{4} \land m \neq 2$ .

C. $m < \frac{9}{4} \land m \neq 2$ .

D. $m > \frac{9}{4}$ .

Hiển thị đáp án

Đáp án: C

Giải thích:

Phương trình $(x^{2} - 3 x + m) (x - 1) = 0$

$\Leftrightarrow [\begin{array}{l} x = 1 \\ x^{2} - 3 x + m = 0 (2) \end{array}$

Phương trình (1) có 3 nghiệm phân biệt

$\Leftrightarrow$ Phương trình (2) có hai nghiệm phân biệt khác 1

$\Leftrightarrow \{\begin{cases} 9 - 4 m > 0 \\ 1 - 3 + m \neq 0 \end{cases} \Leftrightarrow \{\begin{cases} m < \frac{9}{4} \\ m \neq 2 \end{cases}$

Câu 6. Cho phương trình: ${(x^{2} - 2 x + 3)}^{2} + 2 (3 - m) (x^{2} - 2 x + 3) + m^{2} - 6 m = 0$ . Tìm m để phương trình có nghiệm :

A. Mọi m.

B. $m \leq 4$ .

C. $m \leq - 2$ .

D. $m \geq 2$ .

Hiển thị đáp án

Đáp án: D

Giải thích:

Đặt $t = x^{2} - 2 x + 3 (t \geq 2)$ .

Ta được phương trình :

$t^{2} + 2 (3 - m) t + m^{2} - 6 m = 0 (1)$

$Δ^{/} = m^{2} - 6 m + 9 - m^{2} + 6 m = 9$

suy ra phương trình (1) luôn có hai nghiệm là $t_{1} = m - 6$ và $t_{2} = m$ .

theo yêu cầu bài toán ta suy ra phương trình (1) có nghiệm lớn hơn hoặc bằng 2

$\Leftrightarrow [\begin{array}{l} m - 6 \geq 2 \\ m \geq 2 \end{array} \Leftrightarrow m \geq 2$

Câu 7. Tìm tất cả giá trị của m để phương trình: $m \sqrt{2 - x} = \frac{x^{2} - m x + 2}{\sqrt{2 - x}}$ có nghiệm dương:

A. $0 < m \leq 2 \sqrt{6} - 4$ .

B. $1 < m < 3$ .

C. $4 - 2 \sqrt{6} \leq m < 1$ .

D. $2 \sqrt{6} - 4 \leq m < 1$

Hiển thị đáp án

Đáp án: B

Giải thích:

Điều kiện x<2, với điều kiện này thì phương trình đã cho trở thành:

$x^{2} + 2 - 2 m = 0 \Leftrightarrow x^{2} = 2 m - 2$

phương trình đã cho có nghiệm dương khi và chỉ khi :

$0 < 2 m - 2 < 4 \Leftrightarrow 1 < m < 3$

Câu 8. Có bao nhiêu giá trị nguyên của a để phương trình: ${(\frac{x^{2}}{x - 1})}^{2} + \frac{2 x^{2}}{x - 1} + a = 0 (1)$ có đúng 4 nghiệm.

A. 0.

B. 1.

C. 2.

D. 3.

Hiển thị đáp án

Đáp án: A

Giải thích:

Đặt $t = \frac{x^{2}}{x - 1}$

Phương trình (1) thành $t^{2} + 2 t + a = 0 (2)$

Phương trình (1) có đúng 4 nghiệm

$\Leftrightarrow$ phương trình (2) có 2 nghiệm dương phân biệt

$\Leftrightarrow \{\begin{cases} Δ > 0 \\ S > 0 \\ P > 0 \end{cases} \Leftrightarrow \{\begin{cases} 4 - 4 a > 0 \\ - 2 > 0 (v l) \\ a > 0 \end{cases}$

$\Leftrightarrow a \notin \emptyset$

Câu 9. Tìm m để phương trình $(m^{2} - 4) x = m (m + 2)$ có tập nghiệm là R:

A. $m = 2$ .

B. $m = - 2$ .

C. $m = 0$ .

D. $m \neq - 2$ và $m \neq 2$ .

Hiển thị đáp án

Đáp án: B

Giải thích:

Phương trình có vô số nghiệm khi

$\{\begin{cases} m^{2} - 4 = 0 \\ m (m + 2) = 0 \end{cases} \Leftrightarrow m = - 2$

Bởi vậy chọn B.

Câu 10. Phương trình $(m^{2} - 3 m + 2) x + m^{2} + 4 m + 5 = 0$ có tập nghiệm là R khi:

A. $m = - 2$ .

B. $m = - 5$ .

C. $m = 1$ .

D. Không tồn tại m.

Hiển thị đáp án

Đáp án: D

Giải thích:

Phương trình có vô số nghiệm khi:

$\{\begin{cases} m^{2} - 3 m + 2 = 0 \\ m^{2} + 4 m + 5 = 0 \end{cases} \Leftrightarrow m \in \emptyset$

Bởi vậy chọn D.

Câu 11. Phương trình $(m^{2} - 5 m + 6) x = m^{2} - 2 m$ vô nghiệm khi:

A. m=1 .

B. m=6.

C. m=2.

D. m=3.

Hiển thị đáp án

Đáp án: D

Giải thích:

Phương trình có vô nghiệm khi:

$\{\begin{cases} m^{2} - 5 m + 6 = 0 \\ m^{2} - 2 m \neq 0 \end{cases} \Leftrightarrow m = 3$

Bởi vậy chọn D.

Câu 12. Phương trình ${(m + 1)}^{2} x + 1 = (7 m - 5) x + m$ vô nghiệm khi:

A. m=2 hoặc m=3.

B. m=2 .

C. m=1 .

D. m=3.

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có :

${(m + 1)}^{2} x + 1 = (7 m - 5) x + m$

$\Leftrightarrow (m^{2} - 5 m + 6) = m - 1$

Phương trình có vô nghiệm khi :

$\{\begin{cases} m^{2} - 5 m + 6 = 0 \\ m - 1 \neq 0 \end{cases} \Leftrightarrow [\begin{array}{l} m = 2 \\ m = 3 \end{array}$

Bởi vậy chọn A.

Câu 13. Cho phương trình $x^{4} + x^{2} + m = 0$ . Khẳng định nào sau đây là đúng:

A. Phương trình có nghiệm $\Leftrightarrow m \leq \frac{1}{4}$ .

B. Phương trình có nghiệm $m \leq 0$ .

C. Phương trình vô nghiệm với mọi m.

D. Phương trình có nghiệm duy nhất $\Leftrightarrow m = - 2$ .

Hiển thị đáp án

Đáp án: B

Giải thích:

Đặt $t = x^{2} (t \geq 0)$

Phương trình (1) thành $t^{2} + t + m = 0 (2)$

Phương trình (1) vô nghiệm

$\Leftrightarrow$ phương trình (2) vô nghiệm hoặc phương trình (2) có 2 nghiệm âm

$\Leftrightarrow Δ < 0 \cup \{\begin{cases} Δ \geq 0 \\ S < 0 \\ P > 0 \end{cases}$

$\Leftrightarrow 1 - 4 m < 0 \cup \{\begin{cases} 1 - 4 m \geq 0 \\ - 1 < 0 \\ m > 0 \end{cases}$

$\Leftrightarrow m > \frac{1}{4} \cup \{\begin{cases} m \leq \frac{1}{4} \\ m > 0 \end{cases} \Leftrightarrow m > 0$

Phương trình có nghiệm $\Leftrightarrow m \leq 0$ .

Câu 14. Phương trình $- x^{4} + (\sqrt{2} - \sqrt{3}) x^{2} = 0$ có:

A. 1 nghiệm.

B. 2 nghiệm.

C. 3 nghiệm.

D. 4 nghiệm.

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có

$- x^{4} + (\sqrt{2} - \sqrt{3}) x^{2} = 0$

$\Leftrightarrow x^{2} (- x^{2} + \sqrt{2} - \sqrt{3}) = 0$

$\Leftrightarrow [\begin{array}{l} x^{2} = 0 \\ x^{2} = \sqrt{2} - \sqrt{3} (v l) \end{array}$

$\Leftrightarrow x^{2} = 0 \Leftrightarrow x = 0$

Câu 15. Nghiệm của hệ: $\{\begin{cases} \sqrt{2} x + y = 1 \\ 3 x + \sqrt{2} y = 2 \end{cases}$ là:

A. $(\sqrt{2} - 2; 2 \sqrt{2} - 3) .$

B. $(\sqrt{2} + 2; 2 \sqrt{2} - 3) .$

C. $(2 - \sqrt{2}; 3 - 2 \sqrt{2}) .$

D. $(2 - \sqrt{2}; 2 \sqrt{2} - 3) .$

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có: $y = 1 - \sqrt{2} x$

$\Rightarrow 3 x + \sqrt{2} (1 - \sqrt{2} x) = 2$

$\Rightarrow x = 2 - \sqrt{2}$

$\Rightarrow y = 3 - 2 \sqrt{2}$

Câu 16. Hệ phương trình sau có bao nhiêu nghiệm $(x; y) : \{\begin{cases} 2 x + 3 y = 5 \\ 4 x + 6 y = 10 \end{cases}$

A. 0

B. 1

C. 3

D. Vô số.

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có :

$4 x + 6 y = 10 \Leftrightarrow 2 x + 3 y = 5$ .

Vậy phương trình có vô số nghiệm.

Câu 17. Tìm nghiệm của hệ phương trình: $\{\begin{cases} 3 x + 4 y = 1 \\ 2 x - 5 y = 3 \end{cases}$

A. $(\frac{17}{23}; - \frac{7}{23}) .$

B. $(- \frac{17}{23}; \frac{7}{23}) .$

C. $(- \frac{17}{23}; - \frac{7}{23}) .$

D. $(\frac{17}{23}; \frac{7}{23}) .$

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có :

$y = \frac{1 - 3 x}{4} \Rightarrow 2 x - 5 \frac{1 - 3 x}{4} = 1$

$\Rightarrow x = \frac{17}{23} \Rightarrow y = \frac{- 7}{23}$

Câu 18. Tìm nghiệm $(x; y)$ của hệ: $\{\begin{cases} 0, 3 x - 0, 2 y - 0, 33 = 0 \\ 1, 2 x + 0, 4 y - 0, 6 = 0 \end{cases}$

A. $(- 0, 7; 0, 6) .$

B. $(0, 6; - 0, 7) .$

C. $(0, 7; - 0, 6) .$

D. Vô nghiệm.

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có: $y = \frac{0, 3 x - 0, 33}{0, 2}$

$\Rightarrow 1, 2 x + 0, 4 \frac{0, 3 x - 0, 33}{0, 2} - 0, 6 = 0$

$\Rightarrow x = 0, 7 \Rightarrow y = - 0, 6$

Câu 19. Tìm điều kiện của tham số m để hệ phương trình sau có đúng một nghiệm: $\{\begin{cases} 3 x - m y = 1 \\ - m x + 3 y = m - 4 \end{cases}$

A. $m \neq 3$ hay $m \neq - 3$

B. $m \neq 3$ và $m \neq - 3$

C. $m \neq 3$

D. $m \neq - 3$

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có :

$D = |\begin{array}{l} 3 - m \\ - m 3 \end{array}| = 9 - m^{2}$

Phương trình có đúng một nghiệm khi $D \neq 0 \Leftrightarrow m \neq \pm 3$ .

Câu 20. Với giá trị nào của m thì hai đường thẳng sau trùng nhau $(d_{1}) : (m^{2} - 1) x - y + 2 m + 5 = 0$ và $(d_{2}) : 3 x - y + 1 = 0 .$

A. m= - 2

B. m= 2

C. m= 2 hay m= - 2

D. Không có giá trị m.

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có: Hai đường thẳng $d_{1}$ và $d_{2}$ trùng nhau khi

$\frac{m^{2} - 1}{3} = \frac{- 1}{- 1} = \frac{2 m + 5}{1}$

$\Leftrightarrow \{\begin{cases} m^{2} - 1 = 3 \\ 2 m + 5 = 1 \end{cases} \Leftrightarrow \{\begin{cases} m = \pm 2 \\ m = - 2 \end{cases}$

$\Leftrightarrow m = - 2$

Câu 21. Tìm a để hệ phương trình $\{\begin{matrix} a x + y = a^{2} \\ x + a y = 1 \end{matrix}$ vô nghiệm:

A. a=1

B. a=1 hoặc a= - 1.

C. a= - 1.

D. Không có a.

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có : $D = a^{2} - 1$

$D_{x} = a^{3} - 1, D_{y} = a - a^{2}$

Hệ phương trình vô nghiệm

$\Rightarrow D = 0 \Leftrightarrow a = \pm 1$

$a = 1 \Rightarrow D_{x} = D_{y} = 0 \Rightarrow$ Hệ phương trình vô số nghiệm.

$a = - 1 \Rightarrow D_{x} = D_{y} = 0 \Rightarrow$ Hệ phương trình vô nghiệm.

Câu 22. Nghiệm của hệ phương trình: $\{\begin{cases} x + y + z = 9 \\ \frac{1}{x} + \frac{1}{y} + \frac{1}{z} = 1 \\ x y + y z + z x = 27 \end{cases}$

A. (1;1;1)

B. (1;2;1)

C. (2;2;1)

D. (3;3;3)

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có : $\frac{1}{x} + \frac{1}{y} + \frac{1}{z} = 1$

$\Leftrightarrow x y + y z + z x = x y z$

$\Rightarrow x y z = 27$

$\Rightarrow x, y, z$ là nghiệm của phương trình :

$X^{3} - 9 X^{2} + 27 X - 27 = 0$

$\Leftrightarrow X = 3$

Vậy hệ phương trình có nghiệm (3;3;3).

Câu 23. Hệ phương trình $\{\begin{cases} x + y + x y = 5 \\ x^{2} + y^{2} = 5 \end{cases}$ có nghiệm là :

A. (2;1)

B. (1;2)

C. (2;1), (1;2)

D. Vô nghiệm.

Hiển thị đáp án

Đáp án: C

Giải thích:

Đặt $S = x + y$

$P = x y (S^{2} - 4 P \geq 0)$

Ta có : $\{\begin{cases} S + P = 5 \\ S^{2} - 2 P = 5 \end{cases}$

$\Rightarrow S^{2} - 2 (5 - S) = 5$

$\Rightarrow S^{2} + 2 S - 15 = 0$

$\Rightarrow S = - 5; S = 3$

$S = - 5 \Rightarrow P = 10$ (loại)

$S = 3 \Rightarrow P = 2$ (nhận)

Khi đó : x,y là nghiệm của phương trình :

$X^{2} - 3 X + 2 = 0 \Leftrightarrow X = 1; X = 2$

Vậy hệ có nghiệm $(2; 1), (1; 2) .$

Câu 24. Hệ phương trình $\{\begin{cases} x + y + x y = \frac{7}{2} \\ x^{2} y + x y^{2} = \frac{5}{2} \end{cases}$ có nghiệm là :

A. $(3; 2); (- 2; 1) .$

B. $(0; 1), (1; 0) .$

C. $(0; 2), (2; 0) .$

D. $(2; \frac{1}{2}); (\frac{1}{2}; 2) .$

Hiển thị đáp án

Đáp án: D

Giải thích:

Đặt $S = x + y$

$P = x y (S^{2} - 4 P \geq 0)$

Ta có : $\{\begin{cases} S + P = \frac{7}{2} \\ S P = \frac{5}{2} \end{cases}$

$\Rightarrow S, P$ là nghiệm của phương trình :

$X^{2} - \frac{7}{2} X + \frac{5}{2} = 0 \Leftrightarrow X = 1; X = \frac{5}{2}$

Khi $S = 1; P = \frac{5}{2}$ (loại)

Khi $S = \frac{5}{2}; P = 1$ thì x,y là nghiệm của phương trình:

$X^{2} - \frac{5}{2} X + 1 = 0 \Leftrightarrow X = 2; X = \frac{1}{2}$

Vậy hệ phương trình có nghiệm $(2; \frac{1}{2}); (\frac{1}{2}; 2) .$

Câu 25. Nếu biết các nghiệm của phương trình: $x^{2} + p x + q = 0$ là lập phương các nghiệm của phương trình $x^{2} + m x + n = 0$ . Thế thì:

A. $p + q = m^{3}$ .

B. $p = m^{3} + 3 m n$ .

C. $p = m^{3} - 3 m n$ .

D. Một đáp số khác.

Hiển thị đáp án

Đáp án: C

Giải thích:

Gọi $x_{1}, x_{2}$ là nghiệm của $x^{2} + p x + q = 0$

Gọi $x_{3}, x_{4}$ là nghiệm của $x^{2} + m x + n = 0$

Khi đó $x_{1} + x_{2} = - p$

$x_{3} + x_{4} = - m, x_{3} . x_{4} = n$

Theo yêu cầu ta có: $\{\begin{cases} x_{1} = {x_{3}}^{3} \\ x_{2} = {x_{4}}^{3} \end{cases}$

$\Rightarrow x_{1} + x_{2} = {x_{3}}^{3} + {x_{4}}^{3}$

$\Leftrightarrow x_{1} + x_{2} = {(x_{3} + x_{4})}^{3} - 3 x_{3} x_{4} (x_{3} + x_{4})$

$\Rightarrow - p = - m^{3} + 3 m n$

$\Rightarrow p = m^{3} - 3 m n$

Bởi vậy chọn C.

Câu 26. Phương trình: $3 (m + 4) x + 1 = 2 x + 2 (m - 3)$ có nghiệm có nghiệm duy nhất, với giá trị của m là :

A. $m = \frac{4}{3}$ .

B. $m = - \frac{3}{4}$ .

C. $m \neq \frac{10}{3}$ .

D. $m \neq \frac{4}{3}$ .

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có:

$3 (m + 4) x + 1 = 2 x + 2 (m - 3)$

$\Leftrightarrow (3 m + 10) x = 2 m - 7$

Phương trình có nghiệm có nghiệm duy nhất khi:

$3 m + 10 \neq 0 \Leftrightarrow m \neq - \frac{10}{3}$

Bởi vậy chọn C.

Câu 27. Tìm m để phương trình: $(m^{2} - 2) (x + 1) = x + 2$ vô nghiệm với giá trị của là

A. $m = 0$ .

B. $m = \pm 1$ .

C. $m = \pm 2$ .

D. $m = \pm \sqrt[]{3}$ .

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có: $(m^{2} - 2) (x + 1) = x + 2$

$\Leftrightarrow (m^{2} - 3) x = 4 - m^{2}$

Phương trình vô nghiêm khi

$\{\begin{cases} m^{2} - 3 = 0 \\ 4 - m^{2} \neq 0 \end{cases} \Leftrightarrow [\begin{array}{l} m = \sqrt{3} \\ m = - \sqrt{3} \end{array}$

Câu 28. Phương trình $|2 x - 4| - 2 x + 4 = 0$ có bao nhiêu nghiệm ?

A. 0 .

B. 1 .

C. 2 .

D. Vô số.

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có: $|2 x - 4| - 2 x + 4 = 0$

$\Leftrightarrow |2 x - 4| = 2 x - 4$

$\Leftrightarrow 2 x - 4 \geq 0 \cap [\begin{array}{l} 2 x - 4 = 2 x - 4 \\ 2 x - 4 = 4 - 2 x (v l) \end{array}$

$\Leftrightarrow \{\begin{cases} x \geq 2 \\ x \in ℝ \end{cases} \Leftrightarrow x \geq 2$

Các câu hỏi trắc nghiệm Toán lớp 10 có đáp án, chọn lọc khác:

Trắc nghiệm Bất đẳng thức có đáp án

Trắc nghiệm Bất phương trình và hệ bất phương trình một ẩn có đáp án

Trắc nghiệm Dấu nhị thức bậc nhất có đáp án

Trắc nghiệm Hệ bất phương trình bậc nhất hai ẩn có đáp án

Trắc nghiệm Dấu của tam thức bậc hai có đáp án

1 890 31/03/2022

Tải về

Trang trước

Trang sau

Xem thêm các chương trình khác:

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 3 lên lớp 4

Lớp 3 - Sách cũ

Tiếng Anh 3