Trắc nghiệm Các định nghĩa có đáp án – Toán lớp 10

Trắc nghiệm Toán 10 Bài 1: Các định nghĩa

Câu 1: Cho khẳng định sau

(1). 4 điểm A, B, C, D là 4 đỉnh của hình bình hành thì $\overrightarrow{AB}=\overrightarrow{CD}$.

(2). 4 điểm A, B, C, D là 4 đỉnh của hình bình hành thì $\overrightarrow{AD}=\overrightarrow{CB}$.

(3). Nếu $\overrightarrow{AB}=\overrightarrow{CD}$ thì 4 điểm A, B, C, D là 4 đỉnh của hình bình hành.

(4). Nếu $\overrightarrow{AD}=\overrightarrow{CB}$ thì 4 điểm A, B, C, D theo thứ tự đó là 4 đỉnh của hình bình hành.

Hỏi có bao nhiêu khẳng định sai?

A. 1.

B. 2.

C. 3.

D. 4.

Hiển thị đáp án  

Đáp án: B

Giải thích:

Nếu $\overrightarrow{AD}=\overrightarrow{CB}$ thì 4 điểm A, D, B, C theo thứ tự đó là 4 đỉnh của hình bình hành.

Câu 2: Cho đoạn thẳng AB, I là trung điểm của AB. Khi đó:

A.$\overrightarrow{BI}=\overrightarrow{AI}$ .

B. $\overrightarrow{BI}$ cùng hướng với $\overrightarrow{AB}$.     

C.$\left|\overrightarrow{BI}\right|=2\left|\overrightarrow{IA}\right|$ .

D. $\left|\overrightarrow{BI}\right|=\left|\overrightarrow{IA}\right|$.

Hiển thị đáp án  

Đáp án: D

Giải thích:

$\left|\overrightarrow{BI}\right|=\left|\overrightarrow{IA}\right|$ vì I là trung điểm của AB.

Câu 3: Cho $\overrightarrow{AB}\ne \overrightarrow{0}$ và một điểm C, có bao nhiêu điểm D thỏa mãn $\overrightarrow{AB}=\overrightarrow{CD}$.

A. 1.

B. 2.

C. 0.

D. Vô số.

Hiển thị đáp án  

Đáp án: A

Câu 4: Cho $\overrightarrow{AB}$ khác $\overrightarrow{0}$ và cho điểm C. Có bao nhiêu điểm D thỏa mãn $\left|\overrightarrow{AB}\right|=\left|\overrightarrow{CD}\right|$.

A. Vô số.

B. 1 điểm

C. 2 điểm

D. Không có điểm nào.

Hiển thị đáp án  

Đáp án: A

Giải thích:

Ta có $\left|\overrightarrow{AB}\right|=\left|\overrightarrow{CD}\right|\iff AB=CD$. Suy ra tập hợp các điểm D thỏa mãn yêu cầu bài toán là đường tròn tâm C bán kính AB.

Có vô số điểm D thỏa mãn $\left|\overrightarrow{AB}\right|=\left|\overrightarrow{CD}\right|$

Câu 5: Cho $\overrightarrow{AB}\ne \overrightarrow{0}$ và một điểm C, có bao nhiêu điểm D thỏa mãn $\overrightarrow{AB}=\overrightarrow{CD}$.

A. 1.

B. 2.

C. 0.

D. Vô số.

Hiển thị đáp án  

Đáp án: A

Câu 6: Cho lục giác đều ABCDEF tâm O. Số các vectơ bằng $\overrightarrow{OC}$ có điểm đầu và điểm cuối là đỉnh của lục giác là:

A. 4.

B. 2.

C. 7.

D. 9.

Hiển thị đáp án  

Đáp án: B

Giải thích:

Đó là $\overrightarrow{AB}$, $\overrightarrow{ED}$.

Câu 7: Cho tứ giác ABCD. Điều kiện nào là điều kiện cần và đủ để $\overrightarrow{AB}=\overrightarrow{CD}$?

A. ABCD là hình bình hành.

B. ABDC là hình bình hành.

C. AD và BC có cùng trung điểm.

D. AB=CD.

Hiển thị đáp án  

Đáp án: B

Giải thích:

Ta có:

$•\overrightarrow{AB}=\overrightarrow{CD}\Rightarrow \left\{\begin{array}{l}AB//CD\\ AB=CD\end{array}\right.$

$\Rightarrow$ ABDC là hình bình hành.

 Mặt khác, ABDC là hình bình hành 

$\Rightarrow \left\{\begin{array}{l}AB//CD\\ AB=CD\end{array}\right.\Rightarrow \overrightarrow{AB}=\overrightarrow{CD}$

Do đó, điều kiện cần và đủ để $\overrightarrow{AB}=\overrightarrow{CD}$ là ABDC là hình bình hành.

Câu 8: Cho hai điểm phân biệt A, B. Số vectơ ( khác $\overrightarrow{0}$) có điểm đầu và điểm cuối lấy từ các điểm A, B là:

A. 2.

B. 6.

C. 13.

D. 12.

Hiển thị đáp án  

Đáp án: A

Giải thích:

Số vectơ ( khác $\overrightarrow{0}$) là $\overrightarrow{AB}$; $\overrightarrow{BA}$.

Câu 9: Gọi C là trung điểm của đoạn AB. Hãy chọn khẳng định đúng trong các khẳng định sau:

A. $\overrightarrow{CA}=\overrightarrow{CB}$ .

B. $\overrightarrow{AB}$ và $\overrightarrow{AC}$ cùng hướng.

C. $\overrightarrow{AB}$ và $\overrightarrow{CB}$ ngược hướng.

D. $\left|\overrightarrow{AB}\right|=\overrightarrow{CB}$.

Hiển thị đáp án  

Đáp án: B

Giải thích:

Ta có C là trung điểm của đoạn $\overrightarrow{AB}$ và $\overrightarrow{AC}$ cùng hướng.

Câu 10: Cho hình bình hành ABCD tâm O. Gọi P, Q, R lần lượt là trung điểm AB, BC, AD. Lấy 8 điểm trên làm điểm gốc hoặc điểm ngọn các vectơ. Tìm mệnh đề sai:

A. Có 2 vectơ bằng $\overrightarrow{PQ}$

B. Có 4 vectơ bằng $\overrightarrow{AR}$

C. Có 3 vectơ bằng $\overrightarrow{BO}$

D. Có 5 vectơ bằng $\overrightarrow{OP}$

Hiển thị đáp án  

Đáp án: C

Câu 11: Cho bốn điểm A, B, C, D phân biệt. Nếu $\overrightarrow{AB}=\overrightarrow{BC}$ thì có khẳng định nào sau đây đúng

A. B là trung điểm của AC.

B. B nằm ngoài đoạn AC.

C. ABCD là hình bình hành.

D. ABCD là hình vuông.

Hiển thị đáp án  

Đáp án: A

Câu 12: Gọi C là trung điểm của đoạn AB. Hãy chọn khẳng định đúng trong các khẳng định sau:

A. $\overrightarrow{CA}=\overrightarrow{CB}$.

B. $\overrightarrow{AB}$ và $\overrightarrow{AC}$ cùng hướng.

C. $\overrightarrow{AB}$ và $\overrightarrow{CB}$ ngược hướng.

D.$\left|\overrightarrow{AB}\right|=\overrightarrow{CB}$ .

Hiển thị đáp án  

Đáp án: B

Giải thích:

Ta có C là trung điểm của đoạn $\overrightarrow{AB}$ và $\overrightarrow{AC}$ cùng hướng.

Câu 13: Gọi O là giao điểm của hai đường chéo hình chữ nhật ABCD. Mệnh đề nào sau đây đúng?

A. $\overrightarrow{OA}=\overrightarrow{OC}$.

B. $\overrightarrow{OB}$ và $\overrightarrow{OD}$ cùng hướng.

C. $\overrightarrow{AC}$ và $\overrightarrow{BD}$ cùng hướng.

D.$\left|\overrightarrow{AC}\right|=\left|\overrightarrow{BD}\right|$ .

Hiển thị đáp án  

Đáp án: D

Câu 14: Cho hình bình hành ABGE. Đẳng thức nào sau đây đúng.

A. $\overrightarrow{BA}=\overrightarrow{EG}$ .

B. $\overrightarrow{AG}=\overrightarrow{BE}$ .

C. $\overrightarrow{GA}=\overrightarrow{BE}$.

D. $\overrightarrow{BA}=\overrightarrow{GE}$ .

Hiển thị đáp án  

Đáp án: D

Giải thích:

Hình bình hành ABGE $\iff \overrightarrow{BA}=\overrightarrow{GE}$.

Câu 15: Cho tam giác đều ABC. Mệnh đề nào sau đây sai ?

A. $\overrightarrow{AB}=\overrightarrow{BC}$ .

B. $\overrightarrow{AC}\ne \overrightarrow{BC}$ .       

C. $\left|\overrightarrow{AB}\right|=\left|\overrightarrow{BC}\right|$.

D. $\overrightarrow{AB}$ không cùng phương $\overrightarrow{BC}$.

Hiển thị đáp án  

Đáp án: A

Giải thích:

Ta có tam giác đều ABC $\Rightarrow \overrightarrow{AB}$, $\overrightarrow{BC}$ không cùng hướng $\Rightarrow \overrightarrow{AB}\ne \overrightarrow{BC}$.

Câu 16: Chọn khẳng định đúng

A. Hai vec tơ cùng phương thì cùng hướng. 

B. Hai vec tơ cùng hướng thì cùng phương.

C. Hai vec tơ cùng phương thì có giá song song nhau.    

D. Hai vec tơ cùng hướng thì có giá song song nhau.

Hiển thị đáp án  

Đáp án: B

Giải thích:

Hai véc tơ cùng hướng thì cùng phương.

Câu 17: Cho lục giác ABCDEF. Có bao nhiêu vectơ khác vectơ – không có điểm đầu và điểm cuối là đỉnh của lục giác.

A. 20.

B. 12.

C. 30.

D. 16.

Hiển thị đáp án  

Đáp án: C

Giải thích:

Hai điểm phân biệt, chẳng hạn A, B ta xác định được hai vectơ khác vectơ – không  là $\overrightarrow{AB}$,$\overrightarrow{BA}$ .

Một vectơ khác vectơ – không được xác định bởi 2 điểm phân biệt. Do đó có 30 cách chọn 2 điểm trong 4 điểm của tứ giác (có tính thứ tự các điểm) nên có thể lập được 30 vectơ.

Câu 18: Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Trong các khẳng định sau, hãy tìm khẳng định sai?

A. $\overrightarrow{MN}=\overrightarrow{QP}$ .

B. $\overrightarrow{MQ}=\overrightarrow{NP}$ .

C. $\left|\overrightarrow{PQ}\right|=\left|\overrightarrow{MN}\right|$ .

D. $\left|\overrightarrow{MN}\right|=\left|\overrightarrow{AC}\right|$ .

Hiển thị đáp án  

Đáp án: D

Giải thích:

Ta có MN là đường trung bình của tam giác ABC. Suy ra $MN=\frac{1}{2}AC$ hay $\left|\overrightarrow{MN}\right|=\frac{1}{2}\left|\overrightarrow{AC}\right|$

Câu 19: Cho tam giác ABC đều cạnh a và G là trọng tâm. Gọi I là trung điểm của AG. Độ dài của vectơ $\overrightarrow{BI}$ là

A. $a\frac{\sqrt{21}}{6}$ .

B. $a\frac{\sqrt{21}}{3}$ .

C. $a\frac{\sqrt{3}}{6}$ .

D. $a\frac{\sqrt{3}}{2}$ .

Hiển thị đáp án  

Đáp án: A

Giải thích:

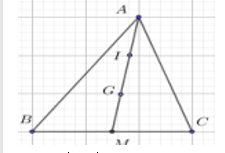
Ta có $\left|\overrightarrow{AB}\right|=AB=a$

Gọi M là trung điểm của BC

Ta có

$\begin{array}{l}\left|\overrightarrow{AG}\right|=AG=\frac{2}{3}AM\\ =\frac{2}{3}\sqrt{A{B}^2-B{M}^2}\\ =\frac{2}{3}\sqrt{a^2-\frac{a^2}{4}}=\frac{a\sqrt{3}}{3}\end{array}$

$\begin{array}{l}\left|\overrightarrow{BI}\right|=BI=\sqrt{B{M}^2+M{I}^2}\\ =\sqrt{\frac{a^2}{4}+\frac{a^2}{3}}=\frac{a\sqrt{21}}{6}\end{array}$

Câu 20: Cho hình bình hành ABCD. Trên các đoạn thẳng DC, AB theo thứ tự lấy các điểm M, N sao cho $DM=BN$. Gọi P là giao điểm của AM, DB và Q là giao điểm của CN, DB. Khẳng định nào đúng?

A. $\overrightarrow{DP}=\overrightarrow{QB}$ .

B. $\overrightarrow{MQ}=\overrightarrow{NP}$ .

C. $\left|\overrightarrow{PQ}\right|=\left|\overrightarrow{MN}\right|$ .

D. $\left|\overrightarrow{MN}\right|=\left|\overrightarrow{AC}\right|$ .

Hiển thị đáp án  

Đáp án: A

Giải thích:

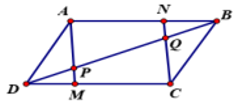
Ta có $DM=BN\Rightarrow AN=MC$, mặt khác AN song song với MC do đó tứ giác ANCM là hình bình hành. Suy ra $\overrightarrow{AM}=\overrightarrow{NC}$.

Xét tam giác $\Delta DMP$ và $\Delta BNQ$ ta có $DM=NB$ (giả thiết), $PDM=QBN$ (so le trong)

Mặt khác $DMP=APB$ (đối đỉnh) và $APQ=NQB$ (hai góc đồng vị) suy ra $DMP=BNQ$.

Do đó $\Delta DMP=\Delta BNQ$ (c.g.c) suy ra $DB=QB$.

Dễ thấy $\overrightarrow{DB}$, $\overrightarrow{QB}$ cùng hướng vì vậy $\overrightarrow{DB}=\overrightarrow{QB}$.

Câu 21: Cho hình thoi ABCD cạnh a và $BAD={60}^o$. Đẳng thức nào sau đây đúng?

A. $\overrightarrow{AB}=\overrightarrow{AD}$ .

B. $\left|\overrightarrow{BD}\right|=a$ .

C. $\overrightarrow{BD}=\overrightarrow{AC}$ .

D. $\overrightarrow{BC}=\overrightarrow{DA}$ .

Hiển thị đáp án  

Đáp án: B

Giải thích:

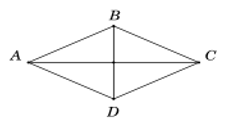
Từ giả thiết suy ra tam giác ABD đều cạnh a nên $\overrightarrow{BD}=a$,$\left|\overrightarrow{BD}\right|=a$.

Câu 22: Cho 3 điểm A, B, C không thẳng hàng, M là điểm bất kỳ. mệnh đề nào sau đây đúng ?

A. $\forall M$ ,$\overrightarrow{MA}=\overrightarrow{MB}$ .

B. $\exists M$ , $\overrightarrow{MA}=\overrightarrow{MB}=\overrightarrow{MC}$.

C. $\forall M$ , $\overrightarrow{MA}\ne \overrightarrow{MB}\ne \overrightarrow{MC}$.

D. $\exists M$ , $\overrightarrow{MA}=\overrightarrow{MB}$.

Hiển thị đáp án  

Đáp án: C

Giải thích:

Ta có 3 điểm A, B, C không thằng hàng, M là điểm bất kỳ.

Suy ra $\overrightarrow{MA}$,$\overrightarrow{MB}$ , $\overrightarrow{MC}$ không cùng phương $\Rightarrow \forall M$,$\overrightarrow{MA}\ne \overrightarrow{MB}\ne \overrightarrow{MC}$ .

Câu 23: Cho ba điểm A, B, C phân biệt. Khi đó:

A. Điều kiện cần và đủ để A, B, C thẳng hàng là $\overrightarrow{AC}$ cùng phương với $\overrightarrow{AB}$.

B. Điều kiện đủ để A, B, C thẳng hàng là $\overrightarrow{CA}$ cùng phương với $\overrightarrow{AB}$. 

C. Điều kiện cần để A, B, C thẳng hàng là $\overrightarrow{CA}$ cùng phương với $\overrightarrow{AB}$.

D. Điều kiện đủ để A, B, C thẳng hàng là $\overrightarrow{AB}=\overrightarrow{AC}$.

Hiển thị đáp án  

Đáp án: A

Giải thích:

Điều kiện cần và đủ để A, B, C thẳng hàng là $\overrightarrow{AC}$ cùng phương với $\overrightarrow{AB}$.

Các vectơ đó là: 

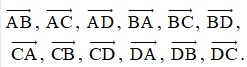
Câu 24: Cho đoạn thẳng AB, I là trung điểm của AB. Khi đó:

A. $\overrightarrow{BI}=\overrightarrow{AI}$.

B. $\overrightarrow{BI}$ cùng hướng với $\overrightarrow{AB}$.     

C.$\left|\overrightarrow{BI}\right|=2\left|\overrightarrow{IA}\right|$ .

D.$\left|\overrightarrow{BI}\right|=\left|\overrightarrow{IA}\right|$ .

Hiển thị đáp án  

Đáp án: D

Giải thích:

$\left|\overrightarrow{BI}\right|=\left|\overrightarrow{IA}\right|$ vì I là trung điểm của AB.

Câu 25: Cho tam giác đều ABC. Mệnh đề nào sau đây là sai?

A. $\overrightarrow{AC}\ne \overrightarrow{BC}$.

B. $\overrightarrow{AB}=\overrightarrow{BC}$ .       

C. $\left|\overrightarrow{AB}\right|=\left|\overrightarrow{BC}\right|$ .

D. $\overrightarrow{AC}$ không cùng phương $\overrightarrow{BC}$.

Hiển thị đáp án  

Đáp án: B

Giải thích:

B. sai do hai vectơ không cùng phương.

Câu 26: Cho hình bình hành ABCD. Các vectơ là vectơ đối của vectơ $\overrightarrow{AD}$ là

A. $\overrightarrow{AD}$, $\overrightarrow{BC}$.

B. $\overrightarrow{BD}$, $\overrightarrow{AC}$.

C. $\overrightarrow{DA}$, $\overrightarrow{CB}$.

D.$\overrightarrow{AB}$ , $\overrightarrow{CB}$.

Hiển thị đáp án  

Đáp án: C

Giải thích:

Vectơ đối của vectơ $\overrightarrow{AD}$ là $\overrightarrow{DA}$, $\overrightarrow{CB}$

Câu 27: Cho lục giác đều ABCDEF tâm O. Ba vectơ bằng vectơ $\overrightarrow{BA}$ là:

A. $\overrightarrow{OF}$,$\overrightarrow{DE}$,$\overrightarrow{OC}$ .

B. $\overrightarrow{CA}$,$\overrightarrow{OF}$,$\overrightarrow{DE}$ .

C. $\overrightarrow{OF}$,$\overrightarrow{DE}$,$\overrightarrow{CO}$.

D. $\overrightarrow{OF}$,$\overrightarrow{ED}$,$\overrightarrow{OC}$.

Hiển thị đáp án  

Đáp án: C

Giải thích:

Ba vectơ bằng vectơ $\overrightarrow{BA}$ là: $\overrightarrow{OF}$,$\overrightarrow{DE}$ , $\overrightarrow{CO}$.

Câu 28: Chọn câu sai:

A. Mỗi vectơ đều có một độ dài, đó là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó.

B. Độ dài của vectơ $\overrightarrow{a}$ được kí hiệu là $\left|\overrightarrow{a}\right|$.   

C. $\left|\overrightarrow{0}\right|=0$,$\left|\overrightarrow{PQ}\right|=\overrightarrow{PQ}$ .    

D.$\left|\overrightarrow{AB}\right|=AB=BA$ .

Hiển thị đáp án  

Đáp án: C

Giải thích:

Vì $\left|\overrightarrow{PQ}\right|=\overrightarrow{PQ}$.

Câu 29: Cho hình bình hành ABCD. Gọi M, N lần lượt là trung điểm của DC, AB; P là giao điểm của AM, DB và Q là giao điểm của CN, DB. Khẳng định nào sau đây là đúng nhất.

A. $\overrightarrow{DM}=\overrightarrow{NB}$ .

B. $\overrightarrow{DP}=\overrightarrow{PQ}=\overrightarrow{QB}$ .

C. Cả A, B đều đúng.

D. Cả A, B đều sai.

Hiển thị đáp án  

Đáp án: C

Giải thích:

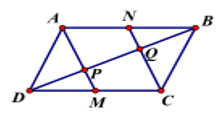
Ta có tứ giác DMBN là hình bình hành vì $DM=NB=\frac{1}{2}AB$, $DM//NB$. Suy ra $\overrightarrow{DM}=\overrightarrow{NB}$.

Xét tam giác CDQ có M là trung điểm của DC và $MP//QC$ do đó P là trung điểm của DQ. Tương tự xét tam giác ABP suy ra được Q là trung điểm của PB

Vì vậy $DP=PQ=QB$ từ đó suy ra $\overrightarrow{DP}=\overrightarrow{PQ}=\overrightarrow{QB}$.

Câu 30: Cho hình thang ABCD có hai đáy là AB và CD với $AB=2CD$. Từ C vẽ $\overrightarrow{CI}=\overrightarrow{DA}$. Khẳng định nào sau đây là đúng nhất?

A.$\overrightarrow{AD}=\overrightarrow{IC}$

B.$\overrightarrow{DI}=\overrightarrow{CB}$

C. Cả A, B đều đúng

D. A đúng, B sai

Hiển thị đáp án  

Đáp án: C

Giải thích:

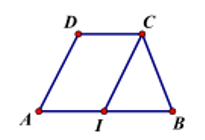
Ta có $\overrightarrow{CI}=\overrightarrow{DA}$ suy ra AICD là hình bình hành

$\Rightarrow \overrightarrow{AD}=\overrightarrow{IC}$

Ta có $DC=AI$ mà $AB=2CD$ do đó $AI=\frac{1}{2}AB\Rightarrow$I là trung điểm AB

Ta có $DC=IB$ và $DC//IB\Rightarrow$tứ giác BCDI là hình bình hành

Suy ra $\overrightarrow{DC}=\overrightarrow{IB}$.

Các câu hỏi trắc nghiệm Toán lớp 10 có đáp án, chọn lọc khác:

Trắc nghiệm Tổng hiệu của hai vecto có đáp án

Trắc nghiệm Tích của vecto với một số có đáp án

Trắc nghiệm Hệ trục tọa độ có đáp án

Trắc nghiệm Bài ôn tập chương 1. Vecto có đáp án

Trắc nghiệm Giá trị lượng giác của một góc bất kì từ 0 độ đến 180 độ có đáp án