Lý thuyết So sánh các phân số. Hỗn số dương đơn giản – Toán lớp 6 Cánh diều

A. Lý thuyết Toán 6 Bài 2: So sánh các phân số. Hỗn số dương đơn giản - Cánh diều

1. So sánh các phân số

a) So sánh hai phân số

Trong hai phân số khác nhau luôn có một phân số nhỏ hơn phân số kia.

- Nếu phân số $\frac{a}{b}$ nhỏ hơn phân số $\frac{c}{d}$ thì ta viết $\frac{a}{b}<\frac{c}{d}$ hay $\frac{c}{d}>\frac{a}{b}.$ 

- Phân số lớn hơn 0 gọi là phân số dương.

- Phân số nhỏ hơn 0 gọi là phân số âm.

- Nếu $\frac{a}{b}<\frac{c}{d}$ và $\frac{c}{d}<\frac{e}{g}$ thì $\frac{a}{b}<\frac{e}{g}.$ 

b) Cách so sánh hai phân số

* So sánh hai phân số cùng mẫu

Trong hai phân số có cùng một mẫu dương, phân số nào có tử lớn hơn thì lớn hơn.

Ví dụ 1. So sánh hai phân số $\frac{1}{3}$ và $\frac{2}{3}$.

Hướng dẫn giải

Ta thấy hai phân số trên cùng mẫu số là 3, tử số của hai phân số là 1 < 2

Nên $\frac{1}{3}<\frac{2}{3}$ hay $\frac{2}{3}>\frac{1}{3}.$ 

Chú ý: Với hai phân số có cùng một mẫu nguyên âm, ta đưa chúng về hai phân số có cùng mẫu nguyên dương rồi so sánh.

Ví dụ 2. So sánh hai phân số $\frac{1}{-3}$ và  $\frac{-2}{-3}$

Hướng dẫn giải

Ta có: $\frac{1}{-3}=\frac{-1}{3}$ và $\frac{-2}{-3}=\frac{2}{3}$ 

Hai phân số có cùng mẫu số là 3, tử số của hai phân số là ‒1 < 2 nên $\frac{-1}{3}<\frac{2}{3}$.

Do đó  $\frac{1}{-3}<\frac{-2}{-3}$.

*So sánh hai phân số không cùng mẫu

Để so sánh hai phân số không cùng mẫu, ta quy đồng mẫu hai phân số đó (về cùng một mẫu dương) rồi so sánh các tử với nhau. Phân số nào có tử lớn hơn thì phân số đó lớn hơn.

Bước 1: Quy đồng mẫu hai phân số đã cho (về cùng một mẫu dương)

Bước 2: So sánh tử của các phân số: Phân số nào có tử lớn hơn thì phân số đó lớn hơn.

Ví dụ 3. So sánh hai phân số $\frac{-3}{8}$ và $\frac{5}{-7}$.

Hướng dẫn giải

Ta có $\frac{5}{-7}=\frac{-5}{7}=\frac{\left(-5\right).8}{7.8}=\frac{-40}{56}$ và $\frac{-3}{8}=\frac{\left(-3\right).7}{8.7}=\frac{-21}{56}$ 

Do ‒40 < ‒21 nên $\frac{-40}{56}<\frac{-21}{56}$.

Vậy $\frac{5}{-7}<\frac{-3}{8}.$ 

2. Hỗn số dương

Viết một phân số lớn hơn 1 thành tổng của một số nguyên dương và một phân số nhỏ hơn 1 (với tử và mẫu dương) rồi viết chúng liền nhau thì được 1 hỗn số dương.

Ví dụ 4.

a) Phân số $\frac{13}{3}=\frac{4.3+1}{3}=\frac{4.3}{3}+\frac{1}{3}=4+\frac{1}{3}=4\frac{1}{3}.$

Do đó phân số $\frac{13}{3}$ còn được viết dưới dạng hỗn số là $4\frac{1}{3}.$  

b) Hỗn số $2\frac{3}{4}=2+\frac{3}{4}=\frac{2.4}{4}+\frac{3}{4}=\frac{8+3}{4}=\frac{11}{4}$.

Do đó hỗn số $2\frac{3}{4}$ viết dưới dạng phân số là $\frac{11}{4}.$  

Bài tập tự luyện

Bài 1. So sánh các phân số sau:

a) $\frac{2}{-5}$ và $\frac{-3}{5}$;

b) $\frac{1}{3}$ và $\frac{5}{6}$;

c) $\frac{5}{-7}$ và $\frac{-7}{11}$;

d) $\frac{5}{6}$ và  $\frac{63}{-70}$.

Hướng dấn giải

a) $\frac{2}{-5}$ và $\frac{-3}{5}$

Ta có: $\frac{2}{-5}=\frac{-2}{5}$

Do ‒2 > ‒3 nên $\frac{-2}{5}>\frac{-3}{5}$.

Vậy $\frac{2}{-5}>\frac{-3}{5}$;

b) $\frac{1}{3}$ và $\frac{5}{6}$

Ta có $\frac{1}{3}=\frac{1.2}{3.2}=\frac{2}{6}$

Vì 2 < 5 nên $\frac{2}{6}<\frac{5}{6}$ 

Vậy $\frac{1}{3}<\frac{5}{6}.$ 

c) $\frac{5}{-7}$ và $\frac{-7}{11}$ 

Ta có: $\frac{5}{-7}=\frac{-5}{7}=\frac{(-5).11}{7.11}=\frac{-55}{77}$ và $-\frac{7}{11}=\frac{-7}{11}=\frac{\left(-7\right).7}{11.7}=\frac{-49}{77}$ 

Vì 55 > 49 nên –55 < –49 do đó $\frac{-55}{77}<\frac{-49}{77}$.

Vậy $\frac{5}{-7}<\frac{-7}{11}.$ 

d) $\frac{5}{6}$ và $\frac{63}{-70}$ 

Ta có: $\frac{5}{6}>0$ và $\frac{63}{-70}<0$

Do đó $\frac{5}{6}>0>\frac{63}{-70}$

Vậy $\frac{5}{6}>\frac{63}{-70}$.

Bài 2. Sắp xếp các số sau theo thứ tự tăng dần: $-\frac{2}{9};\frac{3}{4};-\frac{1}{12};\frac{5}{6};-\frac{5}{8};1\frac{1}{2}.$

Hướng dấn giải

Ta chia các số $-\frac{2}{9};\frac{3}{4};-\frac{1}{12};\frac{5}{6};-\frac{5}{8};1\frac{1}{2}.$ thành hai nhóm:

Nhóm 1: gồm các số $\frac{3}{4};\frac{5}{6};1\frac{1}{2}.$

Nhóm 2: gồm các số $-\frac{2}{9};$$-\frac{1}{12};$$-\frac{5}{8}.$

Ta đi so sánh nhóm 1: $\frac{3}{4};\frac{5}{6};1\frac{1}{2}.$

Có  $\frac{3}{4}=\frac{3.3}{4.3}=\frac{9}{12}$; $\frac{5}{6}=\frac{5.2}{6.2}=\frac{10}{12}$ và $1\frac{1}{2}=1+\frac{1}{2}=\frac{2}{2}+\frac{1}{2}=\frac{3}{2}=\frac{3.6}{2.6}=\frac{18}{12}.$ 

Do 9 < 10 < 18 nên $\frac{9}{12}<\frac{10}{12}<\frac{18}{12}$ 

Vậy $\frac{3}{4}<\frac{5}{6}<1\frac{1}{2}.$ 

Ta đi so sánh nhóm 2: $-\frac{2}{9};$$-\frac{1}{12};$$-\frac{5}{8}.$

Vì $\frac{2}{9}<\frac{5}{9}<\frac{5}{8}$ nên $-\frac{2}{9}>-\frac{5}{8}$

Vì $\frac{2}{9}>\frac{2}{12}>\frac{1}{12}$ nên $-\frac{2}{9}<-\frac{1}{12}$

Do đó $-\frac{5}{8}<-\frac{2}{9}<-\frac{1}{12}$

Trong tất cả các phân số thì phân số âm luôn nhỏ hơn phân số dương, do đó ta có:

$-\frac{5}{8}<-\frac{2}{9}<-\frac{1}{12}<\frac{3}{4}<\frac{5}{6}<1\frac{1}{2}.$

Vậy ta có thể sắp xếp theo thứ tự tăng dần là $-\frac{5}{8};-\frac{2}{9};-\frac{1}{12};\frac{3}{4};\frac{5}{6};1\frac{1}{2}.$

Bài 3. Viết các đại lượng sau dưới dạng phân số và so sánh:

a) Thời gian nào dài hơn: 2 giờ 45 phút hay $2\frac{1}{4}$ giờ?      

b) Vận tốc nào nhỏ hơn: $\frac{5}{6}$ km/h hay $\frac{7}{9}$ km/h?

Hướng dẫn giải

a) Ta có 45 phút = $\frac{45}{60}$ giờ = $\frac{45:15}{60:15}$ giờ = $\frac{3}{4}$ giờ

Do đó 2 giờ 45 phút = $\left(2+\frac{3}{4}\right)$ giờ = $\left(\frac{8}{4}+\frac{3}{4}\right)$ giờ = $\frac{11}{4}$ giờ.

$2\frac{1}{4}$ giờ = $\left(2+\frac{1}{4}\right)$ giờ = $\left(\frac{8}{4}+\frac{1}{4}\right)$ giờ = $\frac{9}{4}$ giờ.

Vì 11 > 9 nên $\frac{11}{4}>\frac{9}{4}$

Do đó 2 giờ 45 phút > $2\frac{1}{4}$ giờ.

Vậy 2 giờ 45 phút dài hơn $2\frac{1}{4}$ giờ.

b) Ta có  $\frac{7}{9}=\frac{7.6}{9.6}=\frac{42}{54}$  và $\frac{5}{6}=\frac{5.9}{6.9}=\frac{45}{54}$

Vì 42 < 45 nên $\frac{42}{54}<\frac{45}{54}$        

Do đó $\frac{7}{9}$ km/h < $\frac{5}{6}$ km/h

Vậy vận tốc $\frac{7}{9}$ km/h nhỏ hơn $\frac{5}{6}$ km/h.

Bài 4. Điền số nguyên thích hợp vào các chỗ trống sau:

a) $\frac{10}{15}<\frac{\mathrm{...}}{15}<\frac{\mathrm{...}}{15}<\frac{\mathrm{...}}{15}<\frac{\mathrm{...}}{15}<\frac{15}{15}$;

b) $\frac{5}{-11}<\frac{\mathrm{...}}{-11}<\frac{\mathrm{...}}{-11}<\frac{\mathrm{...}}{-11}<\frac{1}{-11}$;

Hướng dẫn giải

a) Giả sử $\frac{10}{15}<\frac{a}{15}<\frac{b}{15}<\frac{c}{15}<\frac{d}{15}<\frac{15}{15}$

Ta thấy các phân số trên đều có mẫu số chung là 15, do đó ta có:

10 < a < b < c < d < 15

Mà a, b, c, d là các số nguyên nên a = 11, b = 12, c = 13, d = 14.

Vậy các số nguyên điền vào chỗ trống lần lượt là: 11; 12; 13; 14.

b) Giả sử $\frac{5}{-11}<\frac{x}{-11}<\frac{y}{-11}<\frac{z}{-11}<\frac{1}{-11}$

Suy ra  $\frac{-5}{11}<\frac{-x}{11}<\frac{-y}{11}<\frac{-z}{11}<\frac{-1}{11}$

Do đó ‒5 < ‒x < ‒y < ‒z < ‒1

Hay 5 > x > y > z > 1

Mà x, y, z là các số nguyên nên x = 4, y = 3, z = 2.

Vậy các số nguyên cần điền vào chỗ trống lần lượt là 4; 3; 2.

B. Trắc nghiệm So sánh các phân số. Hỗn số dương đơn giản (Cánh diều 2023) có đáp án

Câu 1. Trong các cách viết sau đây, cách viết nào cho ta phân số:

A. $\frac{12}{0}$

B. $\frac{-4}{5}$

C.$\frac{3}{0,25}$ 

D.$\frac{4,4}{11,5}$

Hiển thị đáp án  

Đáp án: B

Giải thích:

+) $\frac{12}{0}$ không là phân số vì mẫu số bằng 0.

+) $\frac{3}{0,25}$ không là phân số vì mẫu số là số thập phân.

+)  $\frac{4,4}{11,5}$ không là phân số vì tử số và mẫu số là số thập phân.

+) $\frac{-4}{5}$là phân số vì −4;5∈Z và mẫu số là 5 khác 0.

Câu 2. Phần tô màu trong hình sau biểu diễn phân số nào?

A. $\frac{1}{2}$

B. $\frac{1}{4}$

C. $\frac{3}{4}$

B. $\frac{5}{8}$

Hiển thị đáp án  

Đáp án: B

Giải thích:

Trong hình có 2 ô vuông tô màu và tổng tất cả 8 ô vuông nên phân số biểu thị là $\frac{2}{8}=\frac{1}{4}$

Câu 3. Chọn câu sai?

A. $\frac{1}{3}=\frac{45}{135}$

B. $\frac{-13}{20}=\frac{26}{-40}$

C. $\frac{-4}{15}=\frac{-16}{-60}$

D. $\frac{6}{7}=\frac{-42}{-49}$

Hiển thị đáp án  

Đáp án: C

Giải thích:

Đáp án A: Vì 1.135 = 3.45 nên $\frac{1}{3}=\frac{45}{135}$

⇒A đúng.

Đáp án B: Vì (−13).(−40) = 20.26 nên $\frac{-13}{20}=\frac{26}{-40}$

⇒B đúng.

Đáp án C: Vì (−4).(−60) ≠ 15.(−16) nên $\frac{-4}{15}=\frac{-16}{-60}$

⇒C sai.

Đáp án D: Vì 6.(−49) = 7.(−42) nên $\frac{6}{7}=\frac{-42}{-49}$

⇒D đúng.

Câu 4. Điền số thích hợp vào chỗ chấm $\frac{15}{90}=\frac{5}{...}$

A. 20

B. – 60

C. 60

D. 30

Hiển thị đáp án  

Đáp án: D

Giải thích:

$\frac{15}{90}=\frac{5}{x}$

15.x = 90.5

$\mathrm{x}= \frac{90.5}{15}$

x = 30

Vậy số cần điền là: 30

Câu 5. Cho biểu thức $\mathrm{C}=\frac{11}{2\mathrm{n}+1}$. Tìm tất cả các giá trị của n nguyên để giá trị của C là một số tự nhiên.

A. $\mathrm{n}\in \left\{-6,-1,0,5\right\}$

B. $\mathrm{n}\in \left\{-1,5\right\}$

C. $\mathrm{n}\in \left\{0,5\right\}$

D. $\mathrm{n}\in \left\{1,11\right\}$

Hiển thị đáp án  

Đáp án: C

Giải thích:

Vì $\mathrm{C}\in \mathrm{N}\Rightarrow \mathrm{C}\in \mathrm{Z}$. Do đó ta tìm $\mathrm{n}\in \mathrm{Z}$ để $\mathrm{C}\in \mathrm{N}$

Vì $\mathrm{n}\in \mathrm{Z}$ nên để $\mathrm{C}\in \mathrm{Z}$ thì $2\mathrm{n}+1\in \mathrm{U}\left(11\right)=\left\{\pm 1, \pm 11\right\}$

Ta có bảng:

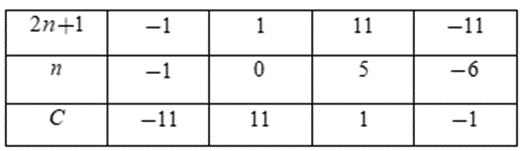
Vì  $\mathrm{C}\in \mathrm{Z}$ nên ta chỉ nhận các giá trị n = 0; n = 5

Câu 6. Có bao nhiêu giá trị nguyên dương của n để $\frac{9}{4\mathrm{n}+1}$ đạt giá trị nguyên.

A. 1

B. 0  

C. 2

D. 3

Hiển thị đáp án  

Đáp án: A

Giải thích:

Vì n nguyên dương nên để $\frac{9}{4\mathrm{n}+1}$ nguyên thì 4n+1∈U(9) = {±1; ±3; ±9}

Ta có bảng:

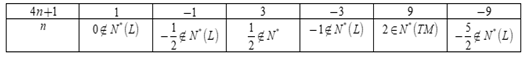
Vậy có duy nhất một giá trị của nn thỏa mãn là n = 2

Câu 7. Tổng các số a, b, c thỏa mãn $\frac{6}{9}=\frac{12}{a}=\frac{b}{-54}=\frac{-738}{c}$ là:

A. 1161

B. – 1125

C. – 1053

D. 1089

Hiển thị đáp án  

Đáp án: B

Giải thích:

Ta có: $\frac{6}{9}=\frac{12}{a}\Rightarrow 6.a=9.12\Rightarrow a=\frac{9.12}{6}=18$

$\frac{6}{9}= \frac{b}{-54}\Rightarrow 6.(-54)=9.b\Rightarrow b=\frac{6.(-54)}{9}=-36$

$\frac{6}{9}=\frac{-738}{c}\Rightarrow 6.c=9.(-738)\Rightarrow \frac{9.(-738)}{6}=-1107$

Vậy a + b + c = 18 + (−36) + (−1107) = −1125

Câu 8. Cho các phân số:  $\frac{15}{60}; \frac{-7}{5}; \frac{6}{15}; \frac{28}{-20}; \frac{3}{12}$

Số cặp phân số bằng nhau trong những phân số trên là:

A. 4

B. 1  

C. 3

D. 2

Hiển thị đáp án  

Đáp án: D

Giải thích:

- Các phân số dương: $\frac{15}{60}; \frac{6}{15};\frac{3}{12}$

+ Vì 15.15 ≠ 60.6 nên $\frac{15}{60}\ne \frac{6}{15}$

+ Vì 6.12 ≠ 15.3 nên$\frac{6}{15}\ne \frac{3}{12}$

+ Vì 15.12 = 60.3 nên  $\frac{15}{60}\ne \frac{3}{12}$

- Các phân số âm: $\frac{-7}{5}; \frac{28}{-20}$

Vì (−7).(−20) = 5.28 nên $\frac{-7}{5}= \frac{28}{-20}$

Vậy có hai cặp phân số bằng nhau trong các phân số đã cho.

Câu 9. Tính tổng các giá trị x∈Z biết rằng $\frac{-111}{37}<x<\frac{91}{13}$

A. 2   

B. 20  

C. 18

D. 15

Hiển thị đáp án  

Đáp án: C

Giải thích:

Ta có:

$-\frac{111}{37}<\mathrm{x}<\frac{91}{13}$⇒−3<x<7

⇒ x ∈ {−2; −1; 0; 1; 2; 3; 4; 5; 6}

Vậy tổng các giá trị của x thỏa mãn là: (−2) + (−1) +...+ 5 + 6 = 18

Câu 10. Tìm tập hợp các số nguyên nn để $\mathrm{A}=\frac{3\mathrm{n}-5}{\mathrm{n}+4}$ có giá trị là số nguyên.

A. n∈{13}    

B. n∈{−21; −5; −3; 13}

C. n∈{−17; −1; 1; 17}                 

D. n∈{−13; −3; 3; 13}

Hiển thị đáp án  

Đáp án: B

Giải thích:

Ta có:

$\mathrm{A}=\frac{3\mathrm{n}-5}{\mathrm{n}+4}=\frac{3\mathrm{n}+12-12-5}{\mathrm{n}+4}=\frac{3(\mathrm{n}+4)+(-17)}{\mathrm{n}+4}$

$=\frac{3(\mathrm{n}+4)}{(\mathrm{n}+4)}+\frac{-17}{\mathrm{n}+4}=3+\frac{-17}{\mathrm{n}+4}$

Vì $\mathrm{n}\in \mathrm{Z}$ nên để $\mathrm{A}\in \mathrm{Z}$ thì $\mathrm{n}+4\in \mathrm{U}(-17)=\left\{\pm 1;\pm 17\right\}$

Ta có bảng:

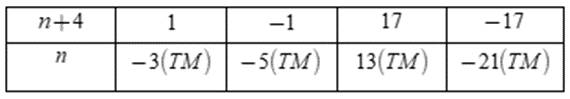
Vậy $\mathrm{n}\in \left\{-21;-5;-3;13\right\}$

Câu 11. Có bao nhiêu cặp số nguyên (x; y) thỏa mãn $\frac{\mathrm{x}}{5}=\frac{3}{y}$ và x  >  y?

A. 4

B. 3     

C. 2

D. 1

Hiển thị đáp án  

Đáp án: A

Giải thích:

Ta có: $\frac{\mathrm{x}}{5}=\frac{3}{y}$⇒ x.y = 5.3 = 15

Mà 15 = 5.3 = 15.1 = (−3).(−5) = (−1).(−15)

 và x,y∈Z, x > y  nên (x;y)∈{(5; 3), (15; 1), (−3; −5), (−1; −15)}

Câu 12. Tìm x; y biết $\frac{\mathrm{x}-4}{\mathrm{y}-3}=\frac{4}{3}$ và x – y = 5.

A. x = 15; y = 5           

B. x = 5; y = 15  

C. x = 20; y = 15                  

D. x = 25; y = 10

Hiển thị đáp án  

Đáp án: C

Giải thích:

Ta có: 

Xx – y = 5 ⇒ x = y + 5 thay vào $\frac{\mathrm{x}-4}{\mathrm{y}-3}=\frac{4}{3}$ ta được:

$\frac{\mathrm{y}+5-4}{\mathrm{y}-3}=\frac{4}{3}$

$\frac{\mathrm{y}+1}{\mathrm{y}-3}=\frac{4}{3}$

3(y + 1) = 4(y − 3)

3y + 3 = 4y − 12

3y − 4y = −12 − 3

−y = −15

y = 15

⇒ x = 15 + 5 = 20

Vậy x = 20; y = 15

Câu 13. Viết số nguyên −16 dưới dạng phân số ta được:

A. $\frac{-16}{0}$

B. $\frac{16}{1}$

C. $\frac{-16}{1}$

D. $\frac{16}{0}$

Hiển thị đáp án  

Đáp án: C

Giải thích:

Viết số nguyên −16 dưới dạng phân số ta được: $\frac{-16}{1}$

Câu 14. Cách viết nào sau đây cho ta một phân số:

A. $\frac{4}{0}$

B. $\frac{1,5}{3}$

C. $\frac{0}{7}$

D. $\frac{-5}{3,5}$

Hiển thị đáp án  

Đáp án: C

Giải thích:

Trả lời:

+ $\frac{4}{0}$ có mẫu bằng 0 nên không là phân số

+ $\frac{1,5}{3}$ có 1,5∉Z nên không là phân số

+ $\frac{0}{7}$ là phân số

+ $\frac{-5}{3,5}$ có 3,5∉Z nên không là phân số

Xem thêm tóm tắt lý thuyết Toán lớp 6 sách Cánh diều hay, chi tiết khác: