Lý thuyết Hình có trục đối xứng chi tiết – Toán lớp 6 Kết nối tri thức
Với lý thuyết Toán lớp 6 Bài 21: Hình có trục đối xứng chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sách Kết nối tri thức sẽ giúp học sinh nắm vững kiến thức trọng tâm để học tốt môn Toán 6.
A. Lý thuyết Toán 6 Bài 21: Hình có trục đối xứng – Kết nối tri thức
1. Hình có trục đối xứng trong thực tế
Các hình có một đường thẳng d chia hình đó thành hai phần mà nếu “gấp” hình theo đường thẳng d thì hai phần đó “chồng khít” lên nhau. Những hình như thế được gọi là hình có trục đối xứng và đường thẳng d là trục đối xứng của nó.
Ví dụ 1. Những hình ảnh có trục đối xứng trong thực tế

2. Trục đối xứng của một số hình phẳng
Mỗi đường thẳng đi qua tâm là một trục đối xứng của hình tròn. Do đó hình tròn có vô số trục đối xứng.
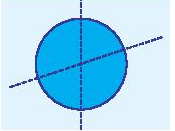
Mỗi đường chéo là một trục đối xứng của hình thoi.
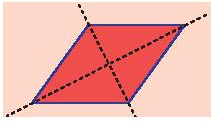
Mỗi đường thẳng đi qua trung điểm hai cạnh đối diện là một trục đối xứng của hình chữ nhật.
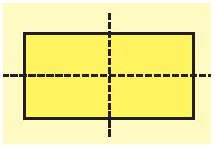
Hình vuông có 4 trục đối xứng bao gồm: Hai đường thẳng đi qua trung điểm hai cạnh đối điện và hai đường chéo.
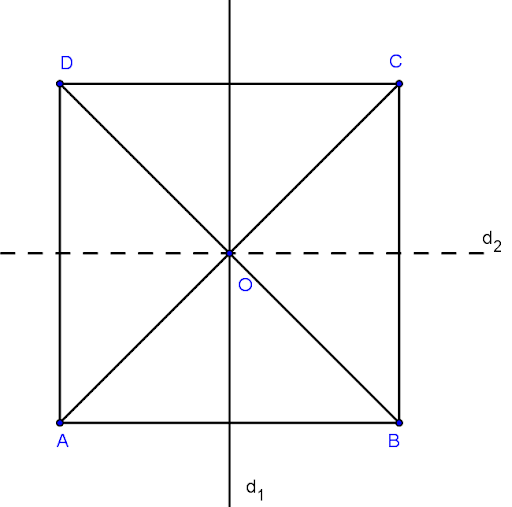
Bài tập
Bài 1. Trong các hình sau đây, hình nào có trục đối xứng.
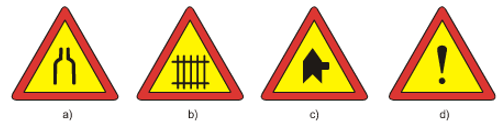
Lời giải
Các hình có trục đối xứng là: Hình a, Hình b, Hình d.
Các trục đối xứng của các hình đó như sau:
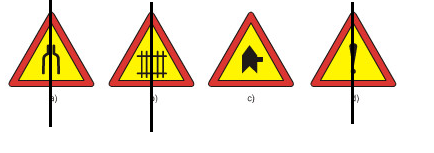
Bài 2. Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai? Vì sao?
(I) Hình vuông là hình có vô số trục đối xứng.
(II) Hình bình hành là hình có trục đối xứng.
(III) Trục đối xứng của hình tròn là đường thẳng đi qua tâm của hình tròn đó.
(IV) Mỗi đường chéo là một trục đối xứng của hình thoi.
Lời giải
(I) Hình vuông là hình có 4 trục đối xứng. Nên (I) là phát biểu sai.
(II) Hình bình hành là hình không có trục đối xứng. Nên (II) là phát biểu sai.
(III) Trục đối xứng của hình tròn là các đường thẳng đi qua tâm. Do đó (III) là phát biểu đúng.
(IV) Hình thoi có hai trục đối xứng là hai đường chéo của hình thoi. Nên (IV) là phát biểu đúng.
Bài 3. Hãy vẽ trục đối xứng của hình sau:

Lời giải
Các trục đối xứng của hình trên được vẽ như sau:

Vậy hình trên có 3 trục đối xứng.
B. Trắc nghiệm Hình có trục đối xứng (Kết nối tri thức 2023) có đáp án
Câu 1. Trong các công trình dưới đây, có bao nhiêu công trình có trục đối xứng?

A. 1
B. 2
C. 3
D. 0
Lời giải Cả ba công trình kiến trúc trên đều có trục đối xứng.
Đáp án: C
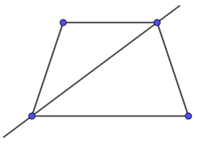
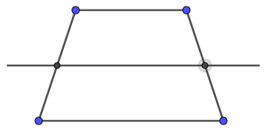
Câu 2. Hình nào dưới đây chỉ ra đúng trục đối xứng của hình thang cân?
A.
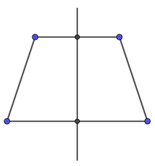
B.
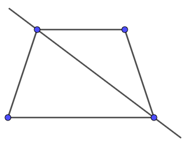
C.
D.
Lời giải
Hình thang cân là hình có một trục đối xứng, trục đối xứng này nối hai trung điểm của hai cạnh đối song song như hình A

Đáp án: A
Câu 3. Hình nào dưới đây có vô số trục đối xứng
A. Hình lục giác đều
B. Hình vuông
C. Hình chữ nhật
D. Hình tròn
Lời giải Hình tròn là hình có vô số trục đối xứng
Đáp án: D
Câu 5. Hình nào dưới đây có trục đối xứng?

A. Hình a), Hình b), Hình c)
B. Hình a), Hình c), Hình d)
C. Hình b), Hình c), Hình d)
D. Hình a) và Hình c)
Lời giải Hình có trục đối xứng là: Hình a), Hình c) và Hình d).
Đáp án: B
Câu 6. Hình vuông có bao nhiêu trục đối xứng:
A. 2
B. 3
C. 4
D. 0
Lời giải
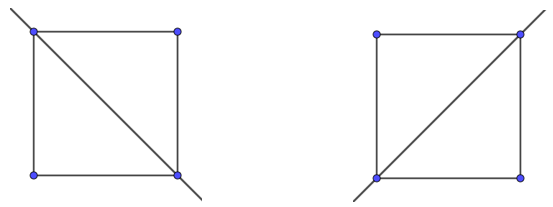
Hình vuông có 4 trục đối xứng, trong đó:
+) 2 trục đối xứng là hai đường chéo của hình vuông.
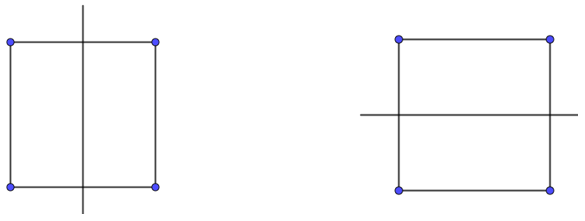
+) 2 trục đối xứng nối trung điểm của hai cạnh đối diện:
Đáp án: C
Câu 7. Trong các loại biển báo sau, biển báo nào có trục đối xứng?

A. Hình a) và Hình c)
B. Hình a) và Hình d)
C. Hình c) và Hình b)
D. Hình c) và Hình d)
Lời giải Hình a) và Hình c) là hai hình có trục đối xứng.
Đáp án: A
Câu 8. Hình nào có số trục đối xứng nhỏ nhất
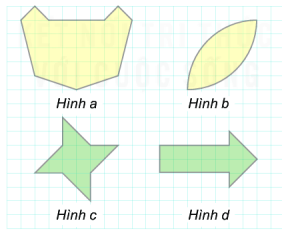
A. Hình a
B. Hình b
C. Hình c
D. Hình d
Lời giải
Hình a) có 1 trục đối xứng:

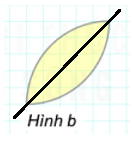
Hình b) có 1 trục đối xứng:
Hình c) không có trục đối xứng.
Hình d) có 1 trục đối xứng

Đáp án: C
Câu 9. Phát biểu nào dưới đây là đúng?
A. Mỗi đường chéo là một trục đối xứng của hình chữ nhật.
B. Mỗi đường thẳng đi qua tâm một đường tròn là trục đối xứng của hình tròn.
C. Mỗi đường thẳng đi qua trung điểm của hai cạnh đối diện là trục đối xứng của hình thoi.
D. Mỗi đường chéo là một trục đối xứng của hình bình hành.
Lời giải
Trục đối xứng của hình chữ nhật là hai đường thẳng đi qua trung điểm của hai cạnh đối nhau. Do đó A sai.
Mỗi đường thẳng đi qua tâm một đường tròn là trục đối xứng của hình tròn. Do đó B đúng.
Mỗi đường chéo là một trục đối xứng của hình thoi. Do đó C sai.
Hình bình hành không có trục đối xứng. Do đó D sai.
Đáp án: B
Câu 10. Trong các chữ cái dưới đây, chữ cái có trục đối xứng?

A. A, H, E
B. A, H
C. A, B, H, E
D. B, E
Lời giải Trong các chữ cái trên có 4 chữ cái có trục đối xứng là: A, B, H, E.
Đáp án: C
Xem thêm tóm tắt lý thuyết Toán lớp 6 sách Kết nối tri thức hay, chi tiết khác:
Lý thuyết Bài 18: Hình tam giác đều. Hình vuông. Hình lục giác đều
Lý thuyết Bài 19: Hình chữ nhật. Hình thoi. Hình bình hành. Hình thang cân
Lý thuyết Bài 20: Chu vi và diện tích của một số hình tứ giác đã học
Xem thêm các chương trình khác:
- Soạn văn lớp 6 (hay nhất) - Kết nối tri thức
- Soạn văn lớp 6 (ngắn nhất) - Kết nối tri thức
- Bộ câu hỏi ôn tập Ngữ văn lớp 6 - Kết nối tri thức
- Bố cục tác phẩm Ngữ văn 6 – Kết nối tri thức
- Nội dung chính tác phẩm Ngữ văn lớp 6 – Kết nối tri thức
- Tóm tắt tác phẩm Ngữ văn lớp 6 – Kết nối tri thức
- Tác giả tác phẩm Ngữ văn lớp 6 – Kết nối tri thức
- Văn mẫu lớp 6 – Kết nối tri thức
- Giải sgk Địa Lí 6 – Kết nối tri thức
- Giải sbt Địa Lí 6 – Kết nối tri thức
- Lý thuyết Địa Lí 6 – Kết nối tri thức
- Giải sgk Tin học 6 – Kết nối tri thức
- Giải sbt Tin học 6 – Kết nối tri thức
- Lý thuyết Tin học 6 – Kết nối tri thức
- Giải sgk Công nghệ 6 – Kết nối tri thức
- Giải sbt Công nghệ 6 – Kết nối tri thức
- Lý thuyết Công nghệ 6 – Kết nối tri thức
- Giải sgk Lịch sử 6 – Kết nối tri thức
- Giải sbt Lịch sử 6 – Kết nối tri thức
- Lý thuyết Lịch sử lớp 6 - Kết nối tri thức
- Giải sgk GDCD 6 – Kết nối tri thức
- Giải sbt GDCD 6 – Kết nối tri thức
- Lý thuyết GDCD 6 – Kết nối tri thức
- Giải sgk Khoa học tự nhiên 6 – Kết nối tri thức
- Giải sbt Khoa học tự nhiên 6 – Kết nối tri thức
- Lý thuyết Khoa học tự nhiên 6 – Kết nối tri thức
- Giải sgk Tiếng Anh 6 – Global Success
- Giải sbt Tiếng Anh 6 – Kết nối tri thức
- Bài tập Tiếng Anh 6 Global success theo Unit có đáp án
- Trọn bộ Từ vựng Tiếng Anh 6 Global success đầy đủ nhất
- Ngữ pháp Tiếng Anh 6 Global success
