Lý thuyết Điểm và đường thẳng – Toán lớp 6 Kết nối tri thức

A. Lý thuyết Toán 6 Bài 32: Điểm và đường thẳng - Kết nối tri thức

1. Điểm thuộc, không thuộc đường thẳng

a) Điểm, đường thẳng

- Dùng bút chấm 1 chấm nhỏ cho ta một hình ảnh về điểm.

- Dùng bút chì và thước thẳng, vẽ được một vạch thẳng cho ta hình ảnh về một đường thẳng.

- Ta thường dùng chữ cái in hoa để đặt tên điểm và dùng chữ cái thường để đặt tên đường thẳng.

Ví dụ 1: 

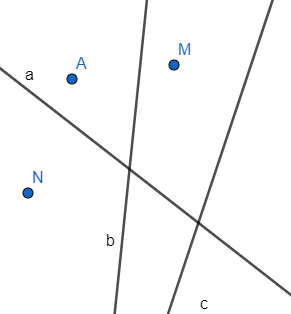
- Điểm M; điểm N; điểm A; …

- Đường thẳng a; đường thẳng b; đường thẳng c; …

b) Điểm thuộc đường thẳng, điểm không thuộc đường thẳng

- Điểm thuộc đường thẳng nếu điểm đó nằm trên đường thẳng đó hay đường thẳng đó đi qua điểm đó.

- Điểm không thuộc đường thẳng nếu điểm đó không nằm trên đường thẳng hay đường thẳng đó không đi qua điểm đó.

- Ta dùng kí hiệu ∈ thể hiện điểm thuộc đường thẳng và ∉ để thể hiện điểm không thuộc đườn thẳng.

Ví dụ 2: 

Quan sát hình vẽ ta có: 

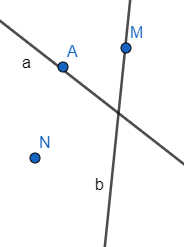
- Điểm A nằm trên đường thẳng a nên A ∈ a.

- Điểm M nằm trên đường thẳng b nên M ∈ b.

- Điểm A không nằm trên đường thẳng b nên A ∉ b.

- Điểm M không nằm trên đường thẳng a nên M ∉ a.

- Điểm N không nằm trên đường thẳng b nên N ∉ b.

- Điểm N không nằm trên đường thẳng a nên N ∉ a.

c) Đường thẳng đi qua hai điểm phân biệt

- Có một đường thẳng và chỉ một đường thẳng đi qua hai điểm phân biệt

Ví dụ 3: Qua hai điểm M, N ta chỉ vẽ được duy nhất một đường thẳng đi qua hai điểm M, N.

Chú ý: Để nhấn mạnh hai phía của đường thẳng, người ta còn dùng hai chữ cái thường để đặt tên, chẳng hạn đường thẳng xy (hoặc yx)

2. Ba điểm thẳng hàng

- Ba điểm thẳng hàng là ba điểm thuộc cùng một đường thẳng.

Ví dụ 4: Cho hai hình vẽ

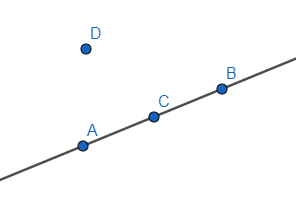
- Quan sát hình vẽ ta thấy

Ba điểm A, B, C thẳng hàng vì nó thuộc cùng một đường thẳng.

Ba điểm A, D, C không thẳng hàng vì nó không thuộc cùng một đường thẳng.

3. Hai đường thẳng song song, cắt nhau, trùng nhau.

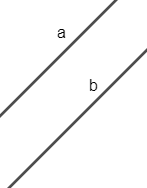
- Hai đường thẳng song song là hai đường thẳng không có điểm chung. Kí hiệu song song là //.

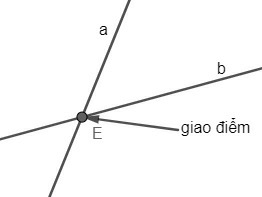
- Hai đường thẳng cắt nhau là hai đường thẳng có một điểm chung.

- Hai đường thẳng trùng nhau là hai đường thẳng có vô số điểm chung.

a và b song song với nhau kí hiệu: a // b	a và b cắt nhau tại điểm E	Đường thẳng AB và đường thẳng BC trùng nhau.

 

Bài tập vận dụng

Bài 1: Cho hình vẽ:

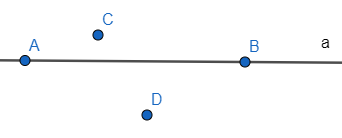
a) Điểm nào thuộc đường thẳng a, trả lời và viết kí hiệu.

b) Điểm nào không thuộc đường thẳng a, trả lời và viết kí hiệu.

Lời giải:

a) Điểm A thuộc đường thẳng a kí hiệu A ∈ a; 

Điểm B thuộc đường thẳng a kí hiệu B ∈ a.

b) Điểm C không thuộc đường thẳng a, kí hiệu C ∉ a;

Điểm D không thuộc đường thẳng a, kí hiệu D ∉ a.

Bài 2: Cho hình vẽ:

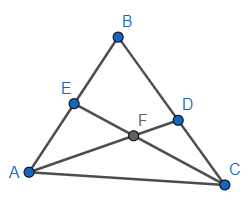
a) Hãy kể tên các bộ ba điểm thẳng hàng.

b) Kể tên ba bộ ba điểm không thẳng hàng.

Lời giải:

a) Các bộ ba điểm thẳng hàng là:

+ A; E; B

+ B; D; C

+ C; E; F

+ D; F; A

b) Ba bộ ba điểm không thẳng hàng là: 

+ A; B; D

+ A; C; F

+ A; B; C

Bài 3: Kể tên các đường thẳng song song trình hình sau: 

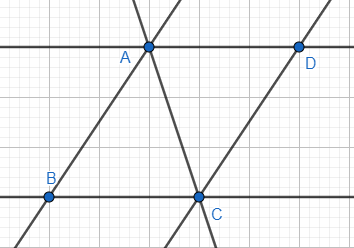
Lời giải: 

Có hai cặp đường thẳng song song AD và BC; AB và CD.

Bài 4: Cho hình vẽ:

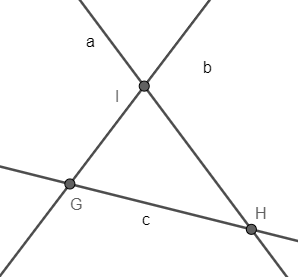
a) Giao điểm của đường thẳng a và đường thẳng b là điểm nào?

b) G là giao điểm của hai đường thẳng nào?

Lời giải:

a) Giao điểm của đường thẳng a và đường thẳng b là điểm I vì I ∈ a và I ∈ b.

b) G là giao điểm của hai đường thẳng b và c vì G ∈ b và G ∈ c.

B. Trắc nghiệm Điểm và đường thẳng (Kết nối tri thức 2023) có đáp án

Câu 1. Dùng kí hiệu để ghi lại cách diễn đạt sau:

“ Đường thẳng aa chứa điểm M và không chứa điểm P . Điểm O thuộc đường thẳng a và không thuộc đường thẳng b.”

A. M∈a; P∉a; O∈a; O∉b                         

B. M∈a; P∉a; O∉a; O∉b         

C. M∉a; P∈a; O∈a; O∉b 

D. M∉a; P∉a; O∈a; O∈b

Hiển thị đáp án  

Đáp án: A

Giải thích:

Kí hiệu cho cách diễn đạt “ Đường thẳng aa chứa điểm M và không chứa điểm P . Điểm O thuộc đường thẳng aa và không thuộc đường thẳng b” là:

M∈a, P∉a, O∈a, O∉b

Đáp án cần chọn là: A

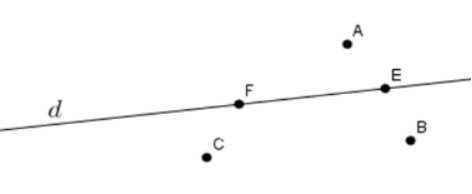
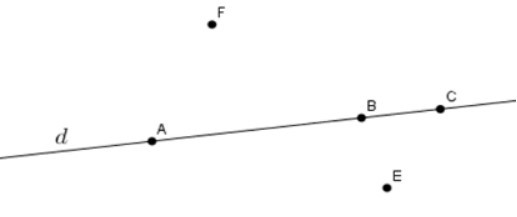
Câu 2. Hình vẽ nào dưới đây thể hiện đúng theo cách diễn đạt: “ Đường thẳng d đi qua các điểm A; B; C nhưng không đi qua các điểm E; F

A.

 

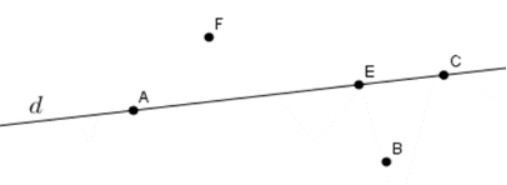
B.

 

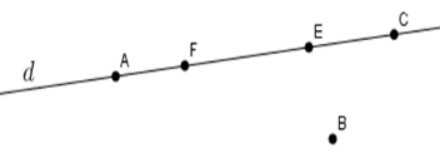
C.

 

D.

 

Hiển thị đáp án  

Đáp án: D

Giải thích:

Cách diễn đạt “ Đường thẳng dd đi qua các điểm A; B; C nhưng không đi qua các điểm E;F được viết dưới dạng kí hiệu là A, B, C ∈ d; E, F ∉ d

Đáp án A: A, B, C∉d; E, F∈d nên A sai.

Đáp án B: A, E, C∈d; B, F∉d nên B sai.

Đáp án C: A, F, E, C∈d; B∉d nên C sai.

Đáp án D: A, B, C∈d; E, F∉d nên D đúng.

Đáp án cần chọn là: D

Câu 3.  Cho hình vẽ sau

 

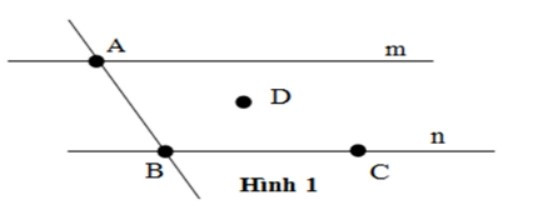
Chọn câu sai.

A. A∈m 

B. A∉n              

C. A∈m; A∈n 

D. A∈m; A∉n

Hiển thị đáp án  

Đáp án: C

Giải thích:

Từ hình vẽ:

Điểm A∈m, A∉n nên A, B, D đúng và C sai.

Đáp án cần chọn là: C

Câu 4.  Cho hình vẽ sau

 

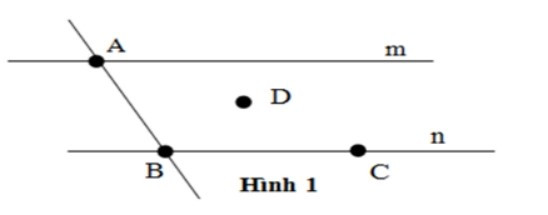
Chọn câu đúng.

A. D∉m                        

B. D∉n  

C. D∈m 

D. Cả A, B đều đúng.

Hiển thị đáp án  

Đáp án: D

Giải thích:

Từ hình vẽ:

Điểm D∉m, D∉n nên D đúng.

Đáp án cần chọn là: D

Câu 5. Cho hình vẽ sau

 

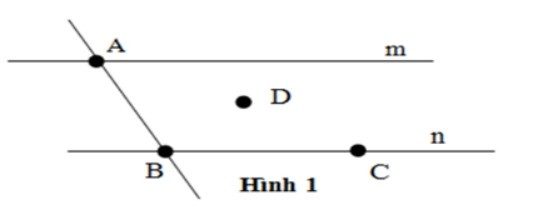
Đường thẳng n đi qua điểm nào?

A. Điểm A                 

B. Điểm B và điểm  C              

C. Điểm B và điểm D               

D. Điểm D và điểm C

Hiển thị đáp án  

Đáp án: B

Giải thích:

Từ hình vẽ:

Đường thẳng nn đi qua các điểm B, C nên đáp án B đúng.

Đáp án cần chọn là: B

Câu 6. Cho hình vẽ sau

 

Chọn câu đúng về đường thẳng m.

A. Đường thẳng m đi qua điểm D.

B. Đường thẳng m đi qua điểm B và điểm C

C. Điểm B và điểm C thuộc đường thẳng m.

D. Đường thẳng m chỉ đi qua điểm A.

Hiển thị đáp án  

Đáp án: D

Giải thích:

Từ hình vẽ:

- Đường thẳng m chỉ đi qua A nên đáp án D đúng.

- Đường thẳng n đi qua hai điểm B, C chứ không phải đường thẳng m nên các đáp án B, C đều sai.

- Cả hai đường thẳng m, n đều không đi qua D nên đáp án A sai

Đáp án cần chọn là: D

Câu 7. Cho hình vẽ sau

 

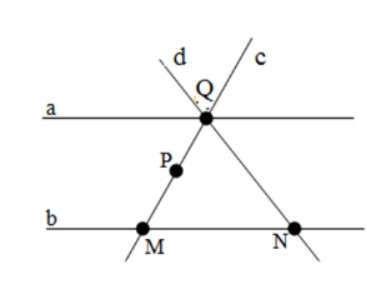
Điểm Q thuộc những đường thẳng nào?

A. a 

B. a; b; c  

C. a; c; d          

D. b;c;d

Hiển thị đáp án  

Đáp án: C

Giải thích:

Từ hình vẽ:

Các đường thẳng a, c, d đều đi qua Q hay điểm Q thuộc các đường thẳng a, c, d

Đáp án cần chọn là: C

Câu 8.  Cho hình vẽ sau

 

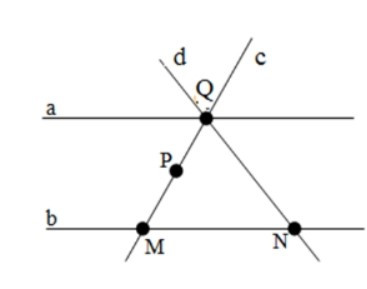
Các đường thẳng nào không đi qua điểm P ? Chọn câu trả lời đúng nhất.

A. b; a; d 

B. a; b; c          

C. c 

D. ab

Hiển thị đáp án  

Đáp án: A

Giải thích:

Từ hình vẽ:

Điểm P chỉ thuộc đường thẳng c và không thuộc các đường thẳng a, b, d

Vậy các đường thẳng a, b, d không đi qua P

Đáp án cần chọn là: A

Câu 9.  Cho hình vẽ sau

 

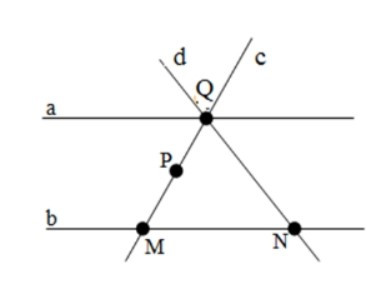
Trên hình vẽ thì hai điểm nào sau đây không cùng thuộc một trong các đường thẳng a; b; c; d ?

A. M; P 

B. N; P            

C. P; Q 

D. N;Q

Hiển thị đáp án  

Đáp án: B

Giải thích:

Từ hình vẽ:

Đáp án A: Hai điểm  M, P cùng thuộc đường thẳng c nên A đúng.

Đáp án B: Điểm P chỉ thuộc đường thẳng c nhưng điểm N không thuộc đường thẳng đó nên hai điểm N, P không cùng thuộc một trong các đường a, b, c, d

Vậy B sai.

Đáp án C: Hai điểm P, Q cùng thuộc đường thẳng c nên C đúng.

Đáp án D: Hai điểm N, Q cùng thuộc đường thẳng d nên D đúng.

Đáp án cần chọn là: B

Câu 10.  Cho hình vẽ sau

 

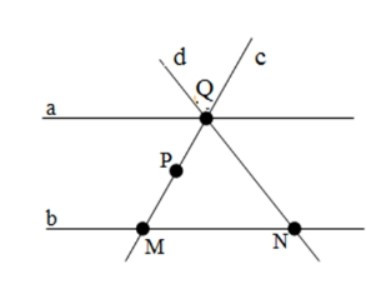
Trên hình vẽ , điểm M thuộc bao nhiêu đường thẳng?

A. 4                

B. 3     

C. 2     

D. 1

Hiển thị đáp án  

Đáp án: C

Giải thích:

Từ hình vẽ ta thấy điểm M thuộc các đường thẳng b, c nên có 2 đường thẳng thỏa mãn.

Đáp án cần chọn là: C

Xem thêm tóm tắt lý thuyết Toán lớp 6 sách Kết nối tri thức hay, chi tiết khác:

Lý thuyết Bài 33: Điểm nằm giữa hai điểm. Tia

Lý thuyết Bài 34: Đoạn thẳng. Độ dài đoạn thẳng

Lý thuyết Bài 35: Trung điểm của đoạn thẳng

Lý thuyết Bài 36: Góc

Lý thuyết Bài 37: Số đo góc