Lý thuyết Dấu hiệu chia hết chi tiết – Toán lớp 6 Kết nối tri thức

A. Lý thuyết Toán 6 Bài 9: Dấu hiệu chia hết – Kết nối tri thức

1. Dấu hiệu chia hết cho 2, cho 5

Các số có chữ số tận cùng là 0, 2, 4, 6, 8 thì chia hết cho 2 và chỉ những số đó mới chia hết cho 2.

Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.

Ví dụ 1. Cho các số sau: 242; 102; 255; 76; 8 090; 260; 145.

a) Các số chia hết cho 2;

b) Các số chia hết cho 5;

c) Các số chia hết cho cả 2 và 5.

Lời giải

a) Các số chia hết cho 2 là các số có chữ số tận cùng là {0; 2; 4; 6; 8}.

Do đó trong các số trên các số chia hết cho 2 là: 242; 102; 76; 8 090; 260.

b) Các số chia hết cho 5 là các số có chữ số tận cùng là 0 hoặc 5.

Do đó trong các số trên số chia hết cho 5 là: 255; 8 090; 260; 145.

c) Các số chia hết cho cả 2 và 5 là: 8 090; 260.

2. Dấu hiệu chia hết cho 9, cho 3

Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9 và chỉ những số đó mới chia hết cho 9.

Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3 và chỉ những số đó mới chia hết cho 3.

Chú ý: Các số chia hết cho 9 thì chia hết cho 3 nhưng chia hết cho 3 chưa chắc chia hết cho 9.

Ví dụ 2. Trong các số sau: 1 954; 264; 315; 705; 2 231; 3 771 số nào chia hết cho 3, số nào chia hết cho 9.

Lời giải

+) Ta có: 1 + 9 + 5 + 4 = 19 không chia hết cho 9 cũng không chia hết cho 3 nên 1954 không chia hết cho 3 và 9.

+) Ta có: 2 + 6 + 4 = 12 chia hết cho 3 nhưng không chia hết cho 9 nên 264 chia hết cho 3 và không chia hết cho 9.

+) Ta có: 3 + 1 + 5 = 9 vừa chia hết cho 3 vừa chia hết cho 9 nên 315 vừa chia hết cho 3 vừa chia hết cho 9.

+) Ta có 7 + 0 + 5 = 12 chia hết cho 3 nhưng không chia hết cho 9 nên 705 chia hết cho 3 và không chia hết cho 9.

+) Ta có 2 + 2 + 3 + 1 = 8 không chia hết cho 3 cũng không chia hết cho 9 nên 2 231 không chia hết cho 3 cũng không chia hết cho 9.

+) Ta có: 3 + 7 + 7 + 1 = 18 vừa chia hết cho 3 vừa chia hết cho 9 nên 3771 vừa chia hết cho 3 vừa chia hết cho 9.

Vậy các số chia hết cho 3 là 264; 315; 705; 3 771; các số chia hết cho 9 là 315; 3 771.

Bài tập

Bài 1. Khối lớp 6 của một trường có 396 học sinh đi dã ngoại. Cô phụ trách muốn chia đều số học sinh của khối 6 thành 9 nhóm. Hỏi cô chia nhóm được như vậy không?

Lời giải

Muốn chia đều số học sinh của khối 6 thành 9 nhóm thì 396 phải chia hết cho 9.

Ta có: 3 + 9 + 6 = 12 + 6 = 18 chia hết cho 9 nên 396 chia hết cho 9.

Do đó cô hoàn toàn có thể chia số học sinh khối 6 thành 9 nhóm.

Bài 2. Thay dấu * bởi một chữ số để số $\overline{317*}$:

a) Chia hết cho 2;

b) Chia hết cho 3;

c) Chia hết cho 5;

d) Chia hết cho 9.

Lời giải

a) Để số đã cho chia hết cho 2 thì $*\in \left\{0;2;4;6;8\right\}$.

Vậy để số đã cho chia hết cho 2 thì * có thể thay thế bằng các chữ số {0; 2; 4; 6; 8}.

b) Ta có: 3 + 1 + 7 + * = 11 + *

Để số đã cho chia hết cho 3 thì 11 + * chia hết cho 3,

Mà * thuộc {0; 1; 2; 3; 4; 5; 6; 7; 8; 9}

Từ đó, Ta có: 11 + 1 =12 chia hết cho 3;

11 + 4 = 15 chia hết cho 3;

11 + 7 = 18 chia hết cho 3

nghĩa là $*\in \left\{1;4;7\right\}$.

Vậy để số đã cho chia hết cho 3 thì * có thể thay thế bằng các chữ số {1; 4; 7}.

c) Để số đã cho chia hết cho 5 thì $*\in \left\{0;5\right\}$.

Vậy để số đã cho chia hết cho 5 thì có thể thay thế * bằng các chữ số {0; 5}.

d) Ta có: 3 + 1 + 7 + * = 11 + *

Để số đã cho chia hết cho 9 thì 11 + * chia hết cho 9

Mà * thuộc {0; 1; 2; 3; 4; 5; 6; 7; 8; 9}

Từ đó, ta có:

11 + 7 = 18 chia hết cho 9.

Vậy để số đã cho chia hết cho 9 ta có thể thay thế * bằng số 7.

B. Trắc nghiệm Dấu hiệu chia hết (Kết nối tri thức 2023) có đáp án

I. Nhận biết

Câu 1. Trong các số sau số nào chia hết cho 2:

A. 102;

B. 1 443;

C. 305;

D. 909.

Hiển thị đáp án

Lời giải

Các số chia hết cho 2 là các số có chữ số tận cùng là 0; 2; 4; 6; 8.

Ta thấy 102 có tận cùng bằng 2 nên 102 chia hết cho 2.

Đáp án: A

Câu 2. Trong các số: 10 203; 450; 305; 194 724; 234 500. Có bao nhiêu số chia hết cho 5.

A. 0;

B. 1;

C. 2;

D. 3.

Hiển thị đáp án

Lời giải

Các số chia hết cho 5 có chữ số tận cùng là 0 hoặc 5 là: 450; 305 và 234 500.

Vậy có 3 số chia hết cho 5.

Đáp án: D

Câu 3. Trong các số: 102; 355; 270; 2 350; 6 708. Số nào chia hết cho cả 2 và 5.

A. 102 và 270.

B. 355 và 2 350.

C. 270 và 2 350.

D. 355 và 6 708.

Hiển thị đáp án

Lời giải Số vừa chia hết cho 2 và 5 là số có tận cùng bằng 0.

Đáp án: C

Câu 4. Trong các số sau số nào chia hết cho 3: 421; 248; 2 020; 2025.

A. 421.

B. 248.

C. 2 020.

D. 2 025.

Hiển thị đáp án

Lời giải

Ta có 4 + 2 +1 = 7 không chia hết cho 3 nên 421 không chia hết cho 3.

Ta có: 2 + 4 + 8 = 14 không chia hết cho 3 nên 248 không chia hết cho 3.

Ta có 2 + 0 + 2 + 0 = 4 không chia hết cho 3 nên 2 020 không chia hết cho 3.

Ta có: 2 + 0 + 2 +5 = 9 chia hết cho 3 nên 2 025 chia hết cho 3.

Đáp án: D

Câu 5. Phát biểu nào dưới đây là đúng?

A. Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 9 và chỉ những số đó mới chia hết cho 9.

B. Các số có chữ số tận cùng là 3; 6; 9 thì chia hết cho 3.

C. Các số có chữ số tận cùng là 0; 2; 4; 6; 8 thì chia hết cho 5.

D. Các số có chữ số tận cùng là 0; 5 thì chia hết cho 5.

Hiển thị đáp án

Lời giải

Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9 và chỉ những số đó mới chia hết cho 9. Do đó A sai.

Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3 và chỉ những số đó mới chia hết cho 3. Do đó B sai.

Các số có chữ số tận cùng là 0; 2; 4; 6 là các số chia hết cho 2. Do đó C sai.

Các số có chữ số tận cùng là 0 hoặc 5 là các số chia hết cho 5. Do đó D đúng

Đáp án: D

II. Thông hiểu

Câu 1. Không thực hiện phép tính, em hãy cho biết phát biểu nào là đúng.

A. 1 953 + 1 975 chia hết cho 9.

B. 2 020 – 938 chia hết cho 2.

C. 1 942 – 1 930 chia hết cho 5.

D. 2 225 + 1 113 chia hết cho 3.

Hiển thị đáp án

Lời giải

Ta có 1 + 9 + 5 + 3 = 18 chia hết cho 9 nên 1 953 chia hết cho 9, nhưng 1 + 9 + 7 + 5 = 22 không chia hết cho 9 nên 1 975 không chia hết cho 9.

Suy ra 1 953 + 1 975 không chia hết cho 9. Do đó A sai.

2 020 và 938 là số có chữ số tận cùng lần lượt là 0 và 8 nên cả hai số đều chia hết cho 2. 

Suy ra 2 020 – 938 chia hết cho 2. Do đó B đúng.

Ta có 1 942 có tận cùng là 2 không chia hết cho 5, còn 1 930 có tận cùng là 0 nên chia hết cho 5. Như vậy 1 942 – 1 930 không chia hết cho 5. Do đó C sai.

Ta có 2 + 2 + 2 + 5 = 11 không chia hết cho 3, 1 + 1 + 1 + 3 = 6 chia hết cho 3. 

Suy ra 2 225 + 1 113 chia hết cho 3. Do đó D sai.

Đáp án: B

Câu 2. Tìm x, y để số 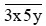 vừa chia hết cho 5, vừa chia hết cho 9.

A. x = 1; y = 0;               

B. x = 3; y = 5;                

C. Cả A và B đều đúng;

D. Cả A và B đều sai.

Hiển thị đáp án

Lời giải

Để số đó chia hết cho 5 thì chữ số tân cùng là 0 hoặc 5.

+) y = 0 

Khi đó số đã cho là 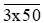 có tổng các chữ số: 3 + x + 5 + 0 = 8 + x.

Để số này chia hết cho 9 thì 8 + x phải chia hết cho 9.

Suy ra x = 1, x = 10, …

Vì x và y là các chữ số nên x và y thuộc nên x = 1.

Vậy x =1; y = 0.

+) y = 5

Khi đó số đã cho là 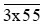 có tổng các chữ số: 3 + x + 5 + 5 = 13 + x.

Để số này chia hết cho 9 thì 13 + x phải chia hết cho 9. 

Suy ra x = 5, x = 14, …

Vì x và y là các chữ số nên x và y thuộc nên x = 5.

Vậy x = 5, y = 5.

Đáp án: C

Câu 3. Dùng ba chữ số 3; 0; 4 để viết các số có ba chữ số khác nhau chia hết cho 2. Hỏi có bao nhiêu số như vậy?

A. 6.

B. 4.

C. 2.

D. 0.

Hiển thị đáp án

Lời giải

Số chia hết cho 2 thì chữ số tận cùng chỉ có thể là 0 hoặc 4.

Nên các số ba chữ số khác nhau lập từ ba chữ số 3; 0; 4 mà chia hết cho 2 là: 304; 340.

Vậy có 2 số như vậy.

Đáp án: C

Câu 4. Từ các chữ số 5; 0; 4; 2. Viết các số tự nhiên có ba chữ số khác nhau sao cho mỗi số đó chia hết cho 3.

A. 2;

B. 4;

C. 6;

D.8.

Hiển thị đáp án

Lời giải

Ta có: 5 + 0 +   4 = 9 chia hết cho 3 nên các số có ba chữ số khác nhau chia hết cho 3 lập từ ba chữ số này là: 504; 540; 405; 450.

Ta có: 0 + 4 + 2 = 6 chia hết cho 3 nên các số có ba chữ số khác nhau chia hết cho 3 lập từ ba chữ số này là: 402; 420; 240; 204.

Vậy có tất cả 8 số.

Đáp án: D

Câu 5. Cho số 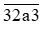 . Ta có thể thay a bởi bao nhiêu chữ số để số 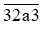chia hết cho 3.

A. 0;

B. 1;

C. 2;

D. 3.

Hiển thị đáp án

Lời giải

Ta có: 3 + 2 + a + 3 = 8 + a.

Để số 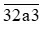  chia hết cho 3 thì 8 + a phải chia hết cho 3.

Suy ra a = 1; a = 4.

Vậy có 2 giá trị của a để số 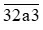 chia hết cho 3.

Đáp án: C

Xem thêm tóm tắt lý thuyết Toán lớp 6 sách Kết nối tri thức hay, chi tiết khác:

Lý thuyết Bài 10: Số nguyên tố

Lý thuyết Bài 11: Ước chung, ước chung lớn nhất

Lý thuyết Bài 12: Bội chung. Bội chung nhỏ nhất

Lý thuyết Bài tập cuối chương 2

Lý thuyết Bài 13: Tập hợp các số nguyên