Lý thuyết Ước chung, ước chung lớn nhất chi tiết – Toán lớp 6 Kết nối tri thức
Với lý thuyết Toán lớp 6 Bài 11: Ước chung, ước chung lớn nhất chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sách Kết nối tri thức sẽ giúp học sinh nắm vững kiến thức trọng tâm để học tốt môn Toán 6.
A. Lý thuyết Toán 6 Bài 11: Ước chung, ước chung lớn nhất – Kết nối tri thức
1. Ước chung và ước chung lớn nhất
Ước chung của hai hay nhiều số là ước của tất cả các số đó.
Ước chung lớn nhất của hai hay nhiều số là số lớn nhất trong tập hợp các ước chung của các số đó.
Ta kí hiệu:
ƯC(a, b) là tập hợp các ước chung của a và b.
ƯCLN(a, b) là ước chung lớn nhất của a và b.
Ví dụ 1.
a) Tìm ước chung của 24 và 60.
b) Tìm ƯCLN (24; 60).
Lời giải
Ư(24) = {1; 2; 3; 4; 6; 8; 12; 24}
Ư (30) = {1; 2; 3; 5; 6; 10; 15; 30}
a) ƯC(24; 30) = {1; 2; 3; 6}
b) ƯCLN(24; 30) = 6.
Nhận xét:
- Trong các số đã cho, nếu số nhỏ nhất là ước của các số còn lại thì ƯCLN của các số đã cho chính là số nhỏ nhất ấy.
Nếu a b thì Ư CLN(a, b) = b.
- Số 1 chỉ có 1 ước là 1. Do đó với mọi số tự nhiên a và b, ta có:
ƯCLN(a, 1) = 1; ƯCLN(a, b, 1) = 1.
Ví dụ 2.
a) Tìm ƯCLN(180, 18)
Vì 180 18 nên ƯCLN(180, 18) = 18.
b) Tìm ƯCLN(13, 1)
Ta có: ƯCLN(13, 1) = 1.
2. Cách tìm ước chung lớn nhất
Các bước tìm ƯCLN của hai hay nhiều số lớn hơn 1:
Bước 1: Phân tích các số ra thừa số nguyên tố.
Bước 2: Chọn ra các thừa số nguyên tố chung.
Bước 3. Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất. Tích đó là ƯCLN phải tìm.
Ví dụ 3. Cách tìm ƯCLN(140, 168)
Ta có: 140 = 22.5.7; 168 = 23.3.7.
Các thừa số chung: 2, 7.
Vậy ƯCLN(140, 168) = 22.7 = 4.7 = 28.
3. Rút gọn về phân số tối giản
Vận dụng ƯCLN để rút gọn về phân số tối giản
Ta rút gọn phân số bằng cách chia cả tử và mẫu của phân số đó cho một ước chung khác 1 (nếu có).
Phân số được gọi là phân số tối giản nếu a và b không có ước chung nào khác 1, nghĩa là ƯCLN(a, b) = 1.
Ví dụ 4. Rút gọn các phân số sau về phân số tối giản
a) ; b) ; c) .
Lời giải
a) ƯCLN(12, 46) = 2.
Để rút gọn phân số ta chia cả tử và mẫu cho ƯCLN của 12 và 46, ta được:
;
b) ƯCLN(35,45) = 5.
Để rút gọn phân số ta chia cả tử và mẫu cho ƯCLN của 35 và 45, ta được:
;
c) ƯCLN(102, 54) = 6.
Để rút gọn phân số ta chia cả tử và mẫu cho ƯCLN của 102 và 54, ta được:
Bài tập
Bài 1. Cho hai số a = 132, b = 36.
a) Phân tích a và b ra thừa số nguyên tố.
b) Tìm ƯCLN(a, b) và ƯC(a, b).
Lời giải
a) 132 = 22.3.11; 36 = 22.32.
b) ƯCLN(132, 36) = 22.3 = 12.
ƯC(132, 36) = {1; 2; 3; 4; 6; 12}.
Bài 2. Các phân số sau đã tối giản chưa? Nếu chưa hãy rút gọn phân số đến phân số tối giản.
a) b) ; c) d)
Lời giải
Tất cả các phân số đã cho đều chưa tối giản.
a) Vì 15050 nên ƯCLN(150, 50) = 50.
Để rút gọn phân số ta chia cả tử và mẫu cho 50, ta được:
b) Ta có: 90 = 2.32.5, 27 = 33.
ƯCLN(90,27) =32 = 9.
Để rút gọn phân số ta chia cả tử và mẫu cho 9, ta được:
c) Ta có: 34 = 2.17, 255 = 3.5.17.
ƯCLN(34, 255) = 17.
Để rút gọn phân số ta chia cả tử và mẫu cho 17, ta được:
d) Ta có: 88 = 23.11, 121 = 112
ƯCLN(88, 121) = 11.
Để rút gọn phân số ta chia cả tử và mẫu cho 11, ta được:
B. Trắc nghiệm Ước chung. Ước chung lớn nhất (Kết nối tri thức 2023) có đáp án
Câu 1. Cho tập Ư(8) = {1; 2; 4; 8} và Ư(20) = {1; 2; 4; 5; 10; 20}. Tập hợp ƯC(8; 20) là:
A. ƯC(8; 20) = {1; 2; 4}.
B. ƯC(8;20) = {1; 2}.
C. ƯC(8; 20) = {1;4}.
D. ƯC(8; 20) = {2;4}.
Lời giải
Các phần tử chung của tập Ư(8) và Ư(20) là: 1; 2; 4.
Do đó ƯC(8; 20) = {1;2;4}.
Đáp án: A
Câu 2. Chọn phát biểu đúng.
A. Ước chung của hai hay nhiều số chỉ có thể là số 1.
B. Ước chung lớn nhất của hai hay nhiều số là ước lớn nhất của số lớn nhất trong các số đó.
C. Ước chung lớn nhất của hai hay nhiều số là số lớn nhất trong tập hợp các ước chung cuả các số đó.
D. Cả A, B, C đều sai.
Lời giải
Ước chung của hai hay nhiều số là ước của tất cả các số đó, không nhất thiết là chỉ có số 1. Do đó A sai.
Ước chung lớn nhất của hai hay nhiều số là số lớn nhất trong tập hợp các ước chung cuả các số đó. Do đó B sai, C đúng, D sai.
Đáp án: C
Câu 3. Sắp xếp các bước tìm ƯCLN của hai hay nhiều số lớn hơn 1 là:
1 – Chọn ra các thừa số nguyên tố chung.
2 – Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất. Tích đó là ƯCLN phải tìm.
3 – Phân tích mỗi số ra thừa số nguyên tố.
A. 1 – 3 – 2;
B. 1 – 2 – 3;
C. 3 – 2 – 1;
D. 3 – 1 – 2;
Lời giải
Các bước tìm ƯCLN của hai hay nhiều số lớn hơn 1 là:
3 – Phân tích mỗi số ra thừa số nguyên tố.
1 – Chọn ra các thừa số nguyên tố chung.
2 – Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất. Tích đó là ƯCLN phải tìm.
Thứ tự đúng là: 3 – 1 – 2.
Đáp án: D
Câu 4. Tìm ƯCLN(90; 10)
A. ƯCLN(90; 10) = 10;
B. ƯCLN(90; 10) = 5;
C. ƯCLN(90; 10) = 90;
D. ƯCLN(90;10) = 1.
Lời giải
Vì 90 = 9.10 nên 90 chia hết cho 10. Do đó ƯCLN(90; 10) = 10.
Đáp án: A
Câu 5. Phân số 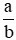 được gọi là phân số tối giản khi:
được gọi là phân số tối giản khi:
A. a và b không có ước chung nào khác 1.
B. a và b có ƯCLN(a, b) = 1.
C. Cả A và B đều đúng.
D. Cả A và B đều sai.
Lời giải
Phân số 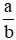 được gọi là phân số tối giản nếu a và b không có ước chung nào khác 1, nghĩa là ƯCLN(a, b) = 1.
được gọi là phân số tối giản nếu a và b không có ước chung nào khác 1, nghĩa là ƯCLN(a, b) = 1.
Đáp án: C
Câu 6. Cho tập ƯC(24; 28) = {1; 2; 4}. Vậy ƯCLN(24; 28) là:
A. 1;
B. 2;
C. 4;
D.24.
Lời giải
Tập ƯC(24; 28) = {1; 2; 4}.
Mà 4 là số lớn nhất trong tập này nên ƯCLN(24, 28) = 4.
Đáp án: C
Câu 7. Tìm ƯCLN(72, 63, 1):
A. 63;
B. 72;
C. 9;
D. 1.
Lời giải
Ta có ƯCLN(a, b, 1) = 1 với a, b là các số tự nhiên.
Vậy ƯCLN(72, 63, 1) = 1.
Đáp án: D
Câu 8. Muốn tìm tập hợp ước chung chung của hai hay nhiều số tự nhiên, ta thực hiện:
A. Tìm ƯCLN của các số đó. Khi đó tập hợp ước chung của các số đó chính là tập hợp ước của ƯCLN.
B. Viết tập hợp các ước của các số đó ra. Tìm trong số đó các phần tử chung. Tập các phần tử đó chính là tập hợp ước chung của các số đó.
C. Cả A và B đều sai.
D. Cả A và B đều đúng.
Lời giải
Muốn tìm tập hợp ước chung chung của hai hay nhiều số tự nhiên, ta có hai cách để tìm như sau:
Cách 1.
- Tìm ƯCLN của các số đó.
- Tìm các ước của ƯCLN đó.
- Kết luận tập hợp ƯC là tập các ước của ƯCLN.
Cách 2.
- Liệt kê tập hợp ước của các số.
- Tìm các phần tử chung của các tập hợp đó.
- Tập hợp ƯC là tập các phần tử chung đó.
Vậy cả A và B đều đúng.
Đáp án: D
Câu 9. Nếu 9 là số lớn nhất sao cho a ⋮ 9 và a ⋮ 9 thì 9 là ………… của a và b. Chọn câu trả lời đúng nhất.
A. ước;
B. ước chung;
C. ước chung lớn nhất;
D. bội.
Lời giải
Nếu 9 là số lớn nhất sao cho a ⋮ 9 và b ⋮ 9 thì 9 là ước chung lớn nhất của a và b.
Đáp án: C
Câu 10. Nếu a ⋮ 7 và a ⋮ 7 thì 7 là ……………… của a và b.
A. ước
B. ước chung;
C. ước chung lớn nhất;
D. bội.
Lời giải
Nếu a ⋮ 7 và b ⋮ 7 thì 7 là ước chung của a và b.
Đáp án: B
Xem thêm tóm tắt lý thuyết Toán lớp 6 sách Kết nối tri thức hay, chi tiết khác:
Lý thuyết Bài 12: Bội chung. Bội chung nhỏ nhất
Lý thuyết Bài tập cuối chương 2
Lý thuyết Bài 13: Tập hợp các số nguyên
Xem thêm các chương trình khác:
- Soạn văn lớp 6 (hay nhất) - Kết nối tri thức
- Soạn văn lớp 6 (ngắn nhất) - Kết nối tri thức
- Bộ câu hỏi ôn tập Ngữ văn lớp 6 - Kết nối tri thức
- Bố cục tác phẩm Ngữ văn 6 – Kết nối tri thức
- Nội dung chính tác phẩm Ngữ văn lớp 6 – Kết nối tri thức
- Tóm tắt tác phẩm Ngữ văn lớp 6 – Kết nối tri thức
- Tác giả tác phẩm Ngữ văn lớp 6 – Kết nối tri thức
- Văn mẫu lớp 6 – Kết nối tri thức
- Giải sgk Địa Lí 6 – Kết nối tri thức
- Giải sbt Địa Lí 6 – Kết nối tri thức
- Lý thuyết Địa Lí 6 – Kết nối tri thức
- Giải sgk Tin học 6 – Kết nối tri thức
- Giải sbt Tin học 6 – Kết nối tri thức
- Lý thuyết Tin học 6 – Kết nối tri thức
- Giải sgk Công nghệ 6 – Kết nối tri thức
- Giải sbt Công nghệ 6 – Kết nối tri thức
- Lý thuyết Công nghệ 6 – Kết nối tri thức
- Giải sgk Lịch sử 6 – Kết nối tri thức
- Giải sbt Lịch sử 6 – Kết nối tri thức
- Lý thuyết Lịch sử lớp 6 - Kết nối tri thức
- Giải sgk GDCD 6 – Kết nối tri thức
- Giải sbt GDCD 6 – Kết nối tri thức
- Lý thuyết GDCD 6 – Kết nối tri thức
- Giải sgk Khoa học tự nhiên 6 – Kết nối tri thức
- Giải sbt Khoa học tự nhiên 6 – Kết nối tri thức
- Lý thuyết Khoa học tự nhiên 6 – Kết nối tri thức
- Giải sgk Tiếng Anh 6 – Global Success
- Giải sbt Tiếng Anh 6 – Kết nối tri thức
- Bài tập Tiếng Anh 6 Global success theo Unit có đáp án
- Trọn bộ Từ vựng Tiếng Anh 6 Global success đầy đủ nhất
- Ngữ pháp Tiếng Anh 6 Global success
