Nội dung bài viết

    Xem thêm

    Lý thuyết Thứ tự thực hiện các phép tính chi tiết – Toán lớp 6 Kết nối tri thức

    Với lý thuyết Toán lớp 6 Bài 7: Thứ tự thực hiện các phép tính chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sách Kết nối tri thức sẽ giúp học sinh nắm vững kiến thức trọng tâm để học tốt môn Toán 6.

    1 992 06/04/2023
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    A. Lý thuyết Toán 6 Bài 7: Thứ tự thực hiện các phép tính – Kết nối tri thức

    + Đối với các biểu thức không có dấu ngoặc:

    - Nếu chỉ có phép cộng và phép trừ (hoặc chỉ có phép nhân và phép chia) thì thực hiện các phép tính từ trái qua phải.

    - Nếu có các phép tính cộng, trừ, nhân, chia, nâng lên lũy thừa thì ta thực hiện phép nâng lên lũy thừa trước, rồi đến nhân và chia, cuối cùng đến cộng và trừ.

    Ví dụ 1. Tính giá trị biểu thức sau:

    a) 23 + 47 – 52;

    b) 24.5:3;

    c) 22.3 + 3.7 – 18:9.

    Lời giải

    a) 23 + 47 – 52

    = 70 – 52

    = 18.

    b) 24.5:3

    = 120 : 3

    = 40.

    c) 22.3 + 3.7 – 18:9

    = 4.3 + 21 – 2

    =12 + 21 – 2

    = 33 – 2

    = 31.

    + Đối với các biểu thức có dấu ngoặc:

    - Nếu chỉ có một dấu ngoặc thì ta thực hiện phép tính trong dấu ngoặc trước.

    - Nếu có các dấu ngoặc tròn (), dấu ngoặc vuông [], dấu ngoặc nhọn {} thì ta thực hiện các phép tính trong dấu ngoặc tròn trước, rồi thực hiện các phép tính trong dấu ngoặc vuông, cuối cùng thực hiện các phép tính trong dấu ngoặc nhọn.

    Ví dụ 2. Thực hiện phép tính

    a) (30 + 80).2 + 20:4;

    b) {52 – 20:[18 – (5 + 9)]}:2

    Lời giải

    a) (30 + 80).2 + 20:4

    = 110.2 + 5

    = 220 + 5

    = 225.

    b) {52 – 20:[18 – (5 + 9)]}:2

    = {25 – 20:[18 – 14]}:2

    = {25 – 20:4}:2

    = {25 – 5}:2

    = 20:2

    =10.

    Bài tập

    Bài 1. Tính giá trị của biểu thức:

    a) 36 – 18:6;

    b) 2.32 – 24:(6.2);

    c) 120 + [55 – (11 – 3.2)2] + 23.

    Lời giải

    a) 36 – 18:6 = 36 – 3 = 33

    b) 2.32 – 24:(6.2)

    = 2.9 – 24:12

    = 18 – 2

    = 16

    c) 120 + [55 – (11 – 3.2)2] + 23

    = 120 + [55 – (11 – 6)2] + 23

    = 120 + [55 – (5)2] + 23

    = 120 + [55 – 25] + 8

    = 120 + 30 + 8

    = 158.

    Bài 2. Tính giá trị của biểu thức:

    a) 1 + 2(a + b) – 43 khi a = 25; b = 9;

    b) [2.x – (23.4 - 16):y].1230 khi x = 8; y = 1.

    Lời giải

    a) Thay a = 25; b = 9 vào biểu thức ta được:

    1 + 2(25 + 9) – 43

    = 1 + 2.34 – 64

    = 1 + 68 – 64

    = 69 – 64

    = 5

    b) Thay x = 8, y = 1 vào biểu thức, ta được:

    [2.8 – (23.4 - 16):1].1230

    = [16 – (8.4 - 16):1].1230

    = [16 – (32 - 16):1].1230

    = [16 – 16:1].1230

    = [16 – 16].1230

    = 0:1230

    = 0

    B. Trắc nghiệm Thứ tự thực hiện các phép tính (Kết nối tri thức 2023) có đáp án

    I. Nhận biết

    Câu 1. Phát biểu nào dưới đây là đúng:

    A. Thực hiện nhân chia trước, cộng trừ sau rồi đến lũy thừa.

    B. Khi thực hiện các phép tính có dấu ngoặc ưu tiên ngoặc vuông trước.

    C. Nếu chỉ có phép cộng, trừ thì ta thực hiện cộng trước trừ sau.

    D. Với các biểu thức có dấu ngoặc: trong ngoặc trước, ngoài ngoặc sau: () → [] → {}.

    Lời giải

    Với các biểu thức không có dấu ngoặc: Lũy thừa → Nhân và chia → Cộng và trừ.

    Với các biểu thức có dấu ngoặc: trong ngoặc trước, ngoài ngoặc sau: () → [] → {}.

    Đáp án: D

    Câu 2. Cho phép tính 12 + 8.3. Bạn Nam thực hiện như sau:

    12 + 8.3

    = (12 + 8).3 (Bước 1)

    = 20.3           (Bước 2)

    = 60.            (Bước 3)

    Bạn Nam sai từ bước nào?

    A. Bước 1.

    B. Bước 2.

    C. Bước 3.

    D. Không sai bước nào.

    Lời giải

    Bạn Nam sai ngay từ bước 1, vì theo thứ tự thực hiện phép tính phải thực hiện nhân chia trước, cộng trừ sau. 

    Sửa lại: 12 + 8.3

    = 12 + 24

    = 36.

    Đáp án: A

    Câu 3. Thứ tự thực hiện phép tính nào sau đây là đúng đối với biểu thức không có dấu ngoặc?

    A. Cộng và trừ → Nhân và chia → Lũy thừa.

    B. Nhân và chia → Lũy thừa → Cộng và trừ.

    C. Lũy thừa → Nhân và chia → Cộng và trừ.

    D. Cả 3 đáp án trên đều đúng.

    Lời giải

    Đối với biểu thức không có dấu ngoặc, thứ tự thực hiện phép tính là: Lũy thừa → Nhân và chia → Cộng và trừ.

    Đáp án: C

    Câu 4. Thứ tự thực hiện phép tính nào sau đây là đúng đối với biểu thức có dấu ngoặc?

    A. [ ] → ( ) → { }.

    B. ( ) → [ ] → { }.

    C. { } → [ ] → ( ).

    D. [ ] → { } → ( ).

    Lời giải

    Đối với biểu thức có dấu ngoặc, thứ tự thực hiện phép tính: ( ) → [ ] → { }.

    Đáp án: B

    Câu 5. Hãy chọn biểu thức sử dụng đúng thứ tự các dấu ngoặc:

    A. 100:{2.[30 − (12 + 7)]}.

    B. 100:[2.(30 − {12 + 7})].

    C. 100:(2.{30 − [12 + 7]}).

    D. 100:(2.[30 − {12 + 7}]).

    Lời giải Biểu thức sử dụng đúng dấu ngoặc là: 100:{2.[30 − (12 + 7)]}.

    Đáp án: A

    II. Thông hiểu

    Câu 1. Tính 14 + 2.82.

    A. 142;

    B. 143;

    C. 144;

    D. 145

    Lời giải 14 + 2.82 = 14 + 2.64 = 14 + 128 = 142.

    Đáp án: A

    Câu 2. 21 là kết quả của phép tính nào dưới đây.

    A. 60 – [120 – (42 – 33)2].

    B. 60 – [90 – (42 – 33)2].

    C. 25.22 – 89.

    D. 8 + 36:3.2.

    Lời giải

    +) 60 – [120 – (42 – 33)2]

    = 60 – [120 – 92]

    = 60 – [120 – 81]

    = 60 – 39

    = 21. Do đó A đúng.

    +) 60 – [90 – (42 – 33)2]

    = 60 – [90 – 92]

    = 60 – [90 – 81]

    = 60 – 9 

    = 51.

    +) 25.22 – 89

    = 25.4 – 89 

    = 100 – 89 

    = 11.

    Đáp án: A

    Câu 3. Tính giá trị của biểu thức 8.(a2 + b2) + 100 tại a = 3, b = 4.

    A. 200.

    B. 300.

    C. 400.

    D. 500.

    Lời giải

    Thay a = 3 và b = 4 vào biểu thức 8.(a2 + b2) + 100 , ta được:

    8.(32 + 42) + 100 

    = 8.(9 + 16) + 100

    = 8.25 + 100

    = 200 + 100

    = 300.

    Đáp án: B

    Câu 4. Tìm giá trị của x thỏa mãn: {23 + [1 + (3 – 1)2]} : x = 13.

    A. x = 1;

    B. x = 2;

    C. x = 3;

    D. x = 0.

    Lời giải

    {23 + [1 + (3 – 1)2]} : x = 13

    {8 + [1 + 22]} : x = 13

    {8 + [1 + 4]} : x = 13

    {8 + 5} : x = 13

    13 : x = 13

    x = 13 : 13

    x = 1.

    Đáp án: A

    Câu 5. Lập biểu thức tính diện tích hình chữ nhật ABCD (hình bên).

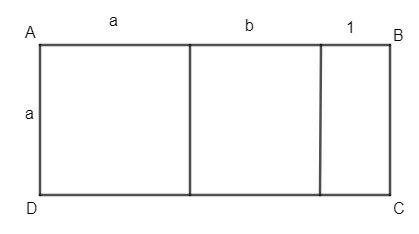
    Bài tập trắc nghiệm Thứ tự thực hiện các phép tính có đáp án - Toán lớp 6 Kết nối tri thức

    A. (a + b + 1 + a).2;

    B. (a + b + 1).a;

    C. 2(a + b + 1).a;

    D. a2 + ab.

    Lời giải

    Chiều dài hình chữ nhật là: a + b +1 (đvđd)

    Diện tích hình chữ nhật là: (a + b + 1).a = a.a + a.b + a.1 = a2 + ab + 1 (đvdt).

    Đáp án: B

    Xem thêm tóm tắt lý thuyết Toán lớp 6 sách Kết nối tri thức hay, chi tiết khác:

    Lý thuyết Bài tập cuối chương 1

    Lý thuyết Bài 8: Quan hệ chia hết và tính chất

    Lý thuyết Bài 9: Dấu hiệu chia hết

    Lý thuyết Bài 10: Số nguyên tố

    Lý thuyết Bài 11: Ước chung, ước chung lớn nhất

    Tham khảo các loạt bài Toán 6 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 992 06/04/2023
    Tải về
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: