Lý thuyết Bội chung. Bội chung nhỏ nhất chi tiết – Toán lớp 6 Kết nối tri thức

A. Lý thuyết Toán 6 Bài 12: Bội chung. Bội chung nhỏ nhất – Kết nối tri thức

1. Bội chung và bội chung nhỏ nhất

Bội chung của hai hay nhiều số là bội của tất cả các số đã cho.

Bội chung nhỏ nhất của hai hay nhiều số là số nhỏ nhất khác 0 trong tập hợp các bội chung của các số đó.

Kí hiệu:

BC(a, b) là tập hợp các bội chung của a và b.

BCNN(a, b) là bội chung nhỏ nhất của a và b.

Ví dụ 1. Tìm bội chung và bội chung nhỏ nhất của 30 và 45

Lời giải

Ta có B(30) = {0; 30; 60; 90; 120; 150; 180; 210; 240; 270; …}

B(45) = {0; 45; 90; 135; 180; 225; 270; …}

BC(30, 45) = {0; 90; 180; 270; …}.

BCNN(30, 45) = 90.

Nhận xét: Trong các số đã cho, nếu số lớn nhất là bội của các số còn lại thì BCNN của các số đã cho chính là số lớn nhất đó.

Nếu a $⋮$ b thì BCNN(a, b) = a.

Mọi số tự nhiên đều là bội của 1. Do đó với mọi số tự nhiên a và b (khác 0), ta có:

BCNN(a, 1) = a; BCNN(a, b, 1) = BCNN(a, b).

Ví dụ 2. Tìm bội chung nhỏ nhất của các số sau:

a) 12 và 36;

b) 124 và 1.

Lời giải

a) Vì 36 $⋮$ 12 nên BCNN(12, 36) = 36;

b) Vì 124 là bội của 1 nên BCNN(1; 124) = 124.

2. Cách tìm bội chung nhỏ nhất

Các bước tìm BCNN của hai hay nhiều số lớn hơn 1:

Bước 1. Phân tích mỗi số ra thừa số nguyên tố;

Bước 2. Chọn ra các thừa số nguyên tố chung và riêng;

Bước 3. Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất. Tích đó là BCNN cần tìm.

Ví dụ 3. Tìm bội chung nhỏ nhất của 21 và 14.

Lời giải

Ta có 21 = 3.7; 14 = 2.7.

Khi đó BCNN(21, 14) = 2.3.7 = 42.

Tìm bội chung từ bội chung nhỏ nhất

Để tìm bội chung của các số đã cho ta có thể làm như sau:

Bước 1. Tìm BCNN của các số đã cho.

Bước 2. Tìm các bội của BCNN đó.

Ví dụ 4. Tìm BC(12, 24, 30)

Lời giải

Ta có: 12 = 2².3; 24 = 2³.3; 30 = 2.3.5.

BCNN(12, 24, 30) = 2³.3.5 = 120.

BC(12, 24, 30) = B(120) = {0; 120; 240; 360; 480; …}.

3. Quy đồng mẫu các phân số

Vận dụng BCNN để tìm mẫu chung của hai phân số:

Để quy đồng mẫu số hai phân số $\frac{a}{b}$ và $\frac{c}{d}$, ta phải tìm mẫu chung của hai phân số đó. Thông thường ta nên chọn mẫu chung là BCNN của hai mẫu.

Ví dụ 5. Quy đồng mẫu số các phân số sau:

a) $\frac{9}{12}$ và $\frac{4}{15}$;                                               b)  $\frac{2}{7};\frac{5}{21}$ và $\frac{8}{14}$.

Lời giải

a) Ta có 12 = 2².3; 15 = 3.5.

BCNN(12, 15) = 2².3.5 = 60.

Ta có: 60:12 = 5; 60:15 = 4. Khi đó:

$\frac{9}{12}=\frac{9.5}{12.5}=\frac{45}{60}$ và $\frac{4}{15}=\frac{4.4}{15.4}=\frac{16}{60}.$

b) Ta có: 7 = 7, 21 = 3. 7, 14 = 2.7.

BCNN(7, 21, 14) = 2.3.7 = 42.

Ta có: 42:7 = 6, 42:21 = 2, 42:14 = 3. Khi đó:

$\frac{2}{7}=\frac{2.6}{7.6}=\frac{12}{42};\frac{5}{21}=\frac{5.2}{21.2}=\frac{10}{42}$ và $\frac{8}{14}=\frac{8.3}{14.3}=\frac{24}{42}.$

Bài tập

Bài 1. Tìm BCNN của các số sau:

a) 27 và 36;

b) 49 và 14.

Lời giải

a) Ta có: 27 = 3³, 36 = 2².3².

Khi đó BCNN(27, 36) = 3³.2² = 27.4 = 108.

Vậy BCNN(27, 36) = 108.

b) Ta có 49 = 7², 14 = 2.7.

Khi đó BCNN(49, 14) = 7².2 = 49.2 = 98.

Vậy BCNN(49, 14) = 98.

Bài 2. Học sinh lớp 6A và 6B khi xếp thành 3 hàng, 5 hàng hay 6 hàng đều vừa đủ. Biết số học sinh của hai lớp từ 70 đến 100 học sinh. Tính số học sinh của lớp 6A và 6B.

Lời giải

Vì số học sinh của lớp 6A và 6B xếp thành 3 hàng, 5 thàng hay 6 hàng đều vừa đủ nghĩa là số học sinh của hai lớp 6A và 6B chia hết cho 3 , 5 và 6 hay số học sinh của lớp 6A và 6B là bội chung của 3, 5 và 6.

Ta có: 3 = 3, 6 = 2.3, 5 = 5.

BCNN(3, 5, 6) = 2.3.5 = 30.

BC(3, 5, 6) = B(30) = {0; 30; 60; 90; 120; …}.

Suy ra $x\in \left\{0;30;60;90;120;\dots \right\}$

Biết số học sinh của hai lớp từ 70 đến 100 học sinh nên số học sinh hai lớp là 90.

Vậy số học sinh của hai lớp 6A và 6B là 90 học sinh.

Bài 3. Thực hiện phép tính:

a) $\frac{7}{11}+\frac{5}{3};$                                                    b) $\frac{2}{15}-\frac{1}{20}$.

Lời giải

a) $\frac{7}{11}+\frac{5}{3}=\frac{7.3}{11.3}+\frac{5.11}{3.11}=\frac{21}{33}+\frac{55}{33}=\frac{21+55}{33}=\frac{76}{33};$

b) $\frac{2}{15}-\frac{1}{20}=\frac{2.4}{15.4}-\frac{1.3}{20.3}=\frac{8}{60}-\frac{3}{60}=\frac{5}{60}=\frac{1}{12}.$

B. Trắc nghiệm Bội chung. Bội chung nhỏ nhất (Kết nối tri thức 2023) có đáp án

Câu 1. Một số tự nhiên a khác 0 nhỏ nhất thỏa mãn 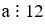 và 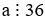 . Khi đó a là:

A. ƯC(12, 36).

B. BC(12, 36).

C. ƯCLN(12, 36).

D. BCNN(12, 36).

Hiển thị đáp án

Lời giải

Vì 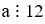  và 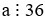  nên a là bội chung của 12 và 36.

Mà a là số tự nhiên khác 0 nhỏ nhất nên a chính là BCNN(12, 36).

Đáp án: D

Câu 2. Sắp xếp các bước tìm BCNN của hai hay nhiều số lớn hơn 1:

1 – Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lấy với số mũ lớn nhất. Tích đó là BCNN cần tìm.

2 – Chọn ra các thừa số nguyên tố chung và riêng.

3 – Phân tích mỗi số ra thừa số nguyên tố.

A. 1 – 2 – 3.

B. 2 – 3 – 1.

C. 3 – 1 – 2.

D. 3 – 2 – 1.

Hiển thị đáp án

Lời giải

Các bước tìm BCNN của hai hay nhiều số lớn hơn 1:

3 – Phân tích mỗi số ra thừa số nguyên tố.

2 – Chọn ra các thừa số nguyên tố chung và riêng.

1 – Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lấy với số mũ lớn nhất. Tích đó là BCNN cần tìm.

Đáp án: D

Câu 3. Bội chung của hai hay nhiều số là gì: 

A. là một tập hợp.

B. là ước của tất cả các số đó.

C. là bội của tất cả các số đó.

D. A, B và C đều đúng.

Hiển thị đáp án

Lời giải Bội chung của hai hay nhiều số là bội của tất cả các số đó.

Đáp án: C

Câu 4. Nếu x  a, x b thì:

A. x ∈ BC(a, b).

B. x là BCNN(a, b).

C. x ∈ ƯC(a,b).

D. x là ƯCLN(a, b).

Hiển thị đáp án

Lời giải

Nếu 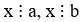  thì x BC(a, b).

Đáp án: B

Câu 5. Mọi số tự nhiên a và b khác 0 ta có:

A. BCNN(a, b, 1) = a.

B. BCNN(a, b, 1) = b.

C. BCNN(a, b, 1) = 1.

D. BCNN(a, b, 1) = BCNN(a, b).

Hiển thị đáp án

Lời giải

Mọi số tự nhiên đều là bội của 1. Do đó với  mọi số tự nhiên a và b (khác 0), ta có:

BCNN(a, b, 1) = BCNN(a, b).

Đáp án: D

Câu 6. Cho biết BC(4, 6) = {0; 12; 24; 36; 48; …}. Hãy cho biết BCNN(4, 6).

A. BCNN(4,6) = 0.

B. BCNN(4, 6) = 12.

C. BCNN(4, 6) = 24.

D. BCNN(4, 6) = 36.

Hiển thị đáp án

Lời giải

Trong tập hợp BC(4, 6) ta thấy bội chung nhỏ nhất khác 0 là 12.

Nên BCNN(4, 6) = 12.

Đáp án: B

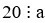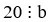Câu 7. Nếu   và   thì 20 là ………………….. của a và b.

A. ước chung.

B. bội chung.

C. ước chung lớn nhất.

D. bội chung nhỏ nhất.

Hiển thị đáp án

Lời giải

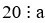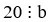Nếu   và   thì 20 là bội chung của a và b.

Đáp án: B

Câu 8. Nếu 30 là số tự nhiên nhỏ nhất mà 30  a và 30  b thì 30 là …………….. của a và b.

A. ước chung.

B. bội chung.

C. ước chung lớn nhất.

D. bội chung nhỏ nhất.

Hiển thị đáp án

Lời giải Nếu 30 là số tự nhiên nhỏ nhất mà 30  a và 30  b thì 30 là bội chung nhỏ nhất của a và b.

Đáp án: D

Câu 9. Cho m = 3.5² và n = 5².7. Tìm ƯCLN(m, n):

A. 5;

B. 25;

C. 75;

D. 105.

Hiển thị đáp án

Lời giải

Ta có: m = 3.5² và n = 5².7.

Tích các thừa số chung với số mũ nhỏ nhất là: 5². 

ƯCLN(m, n) = 5² = 25.

Đáp án: B

Câu 10. Cho m = 2².3.5 và n = 2.3².5. Tìm BCNN(m, n):

A. 30;

B. 60;

C. 90;

D. 180.

Hiển thị đáp án

Lời giải

Ta có m = 2².3.5 và n = 2.3².5

Tích các thừa số chung và riêng với số mũ lớn nhất là: 2².3².5 = 180.

BCNN(m, n) = 180.

Đáp án: D

Xem thêm tóm tắt lý thuyết Toán lớp 6 sách Kết nối tri thức hay, chi tiết khác:

Lý thuyết Bài tập cuối chương 2

Lý thuyết Bài 13: Tập hợp các số nguyên

Lý thuyết Bài 14: Phép cộng và phép trừ số nguyên

Lý thuyết Bài 15: Quy tắc dấu ngoặc

Lý thuyết Bài 16: Phép nhân số nguyên