Nội dung bài viết

    Xem thêm

    Giải Toán 7 trang 94 Tập 1 Cánh diều

    Với giải bài tập Toán lớp 7 trang 94 Tập 1 trong Bài 1: Góc ở vị trí đặc biệt sách Cánh diều hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 7 trang 94 Tập 1.

    1 467 15/01/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 7 trang 94 Tập 1

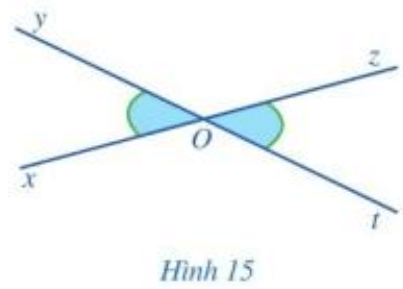
    Hoạt động 6 trang 94 Toán lớp 7 Tập 1: Quan sát Hình 15 và giải thích vì sao:

    Quan sát Hình 15 và giải thích vì sao: Hai góc xOy và yOz là hai góc kề bù

    a) Hai góc xOy và yOz là hai góc kề bù;

    b) Hai góc yOz và zOt là hai góc kề bù;

    c) xOy^+yOz^=yOz^+zO t^ và xOy^=zOt^.

    Lời giải:

    a) Góc xOy có đỉnh là O và hai cạnh là Ox; Oy.

    Góc yOz có đỉnh là O và hai cạnh là Oy; Oz.

    Mặt khác: Ox; Oz nằm về hai phía so với đường thẳng chứa Oy

    Nên hai góc xOy và yOz kề nhau (1)

    Suy ra xOz^=xOy^+yOz^.

    Mà xOz^=180o(do hình vẽ xz là một đường thẳng) nên xOy^+yOz^=180o.

    Do đó, hai góc xOy và yOz bù nhau (2)

    Từ (1) và (2) suy ra: Hai góc xOy và yOz là hai góc kề bù.

    b) Góc yOz có đỉnh là O và hai cạnh là Oz; Oy.

    Góc zOt có đỉnh là O và hai cạnh là Ot; Oz.

    Mặt khác: Oy; Ot nằm về hai phía so với đường thẳng chứa Oz

    Nên hai góc yOz và zOt kề nhau (3)

    Suy ra yOt^=yOz^+zOt^.

    Mà yOt^=180o (do hình vẽ yt là một đường thẳng) nên yOz^+zOt^=180o.

    Do đó, hai góc yOz và zOt bù nhau (4)

    Từ (3) và (4) suy ra: Hai góc yOz và zOt là hai góc kề bù.

    c) Vì xOy^+yOz^=180o và yOz^+zOt^=180o.

    Nên xOy^+yOz^=yOz^+zO t^.

    Suy ra xOy^+yOz^−yOz^=yOz^+zO t^−yOz^ (ta trừ cả hai vế cho yOz^)

    Do đó xOy^=zOt^.

    Vậy xOy^+yOz^=yOz^+zO t^ và xOy^=zOt^.

    Luyện tập 4 trang 94 Toán lớp 7 Tập 1: Tìm số đo x trong Hình 17.

    Tìm số đo x trong Hình 17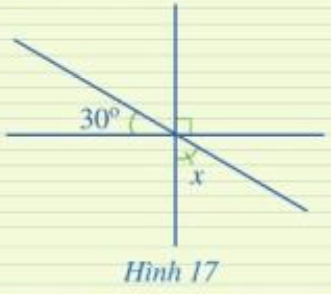Lời giải:

    Đặt tên các đường thẳng ac, bd và eg cùng đi qua điểm O (như hình vẽ).


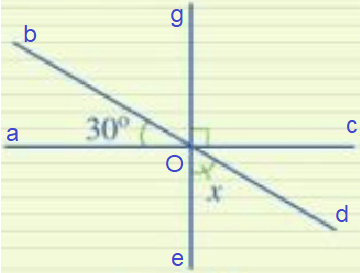
    Tìm số đo x trong Hình 17

    Vì ge và ac là hai đường thẳng vuông góc với nhau nên aOg^=gOc^=cOe^=eOa^=90°

    Ta có: Góc aOb có đỉnh là O và hai cạnh là Oa; Ob.

    Góc bOg có đỉnh là O và hai cạnh là Ob và Og.

    Do đó, aOb và bOg có đỉnh O và cạnh Ob chung.

    Lại có: Oa; Ob nằm về hai phía so với đường thẳng chứa Ob nên aOb và bOg kề nhau

    Khi đó: aOb^+bOg^=aOg^

    Hay 30°+bOg^=90°

    Suy ra, bOg^=90°−30°=60°

    Lại có: Ob là tia đối của tia Od; Og là tia đối của tia Oe nên góc bOg đối đỉnh với góc dOe.

    Suy ra, bOg^=dOe^=60°

    Vậy x = 60°.

    Bài tập

    Bài 1 trang 94, 95 Toán lớp 7 Tập 1:

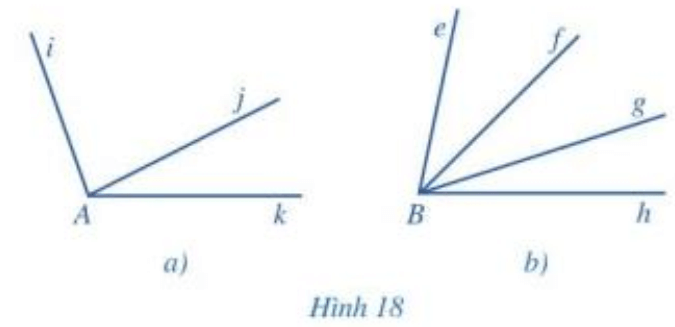
    a) Tìm hai góc kề nhau trong mỗi hình 18a, 18b:

    Tìm hai góc kề nhau trong mỗi hình 18a, 18b

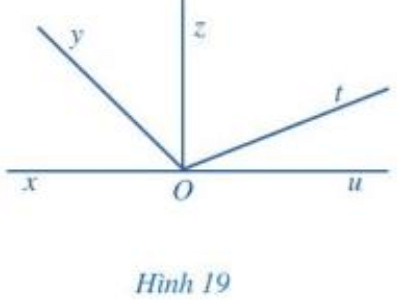
    b) Tìm hai góc kề bù trong Hình 19.

    Tìm hai góc kề nhau trong mỗi hình 18a, 18bc) Tìm hai góc đối đỉnh trong mỗi hình 20a, 20b, 20c, 20d:

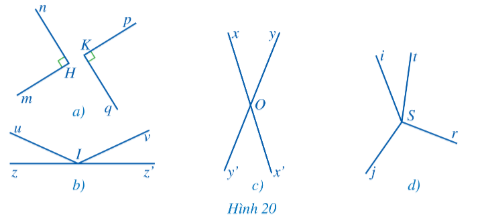
    Toán 7 Bài 1: Góc ở vị trí đặc biệt- Cánh diều (ảnh 1)

    Lời giải:

    a) Xét hình 18a:

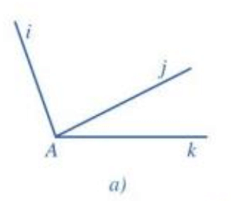
    Tìm hai góc kề nhau trong mỗi hình 18a, 18b

    Hai góc iAj và jAk có chung đỉnh A, chung cạnh Aj và hai cạnh Ai và Ak nằm về hai phía của đường thẳng chứa Aj.

    Do đó, hai góc iAj và jAk kề nhau.

    Xét hình 18b:

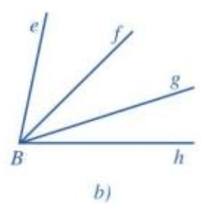
    Tìm hai góc kề nhau trong mỗi hình 18a, 18b

    - Hai góc hBg và gBf có chung đỉnh B, chung cạnh Bg và hai cạnh Bh và Bf nằm về hai phía của đường thẳng chứa Bg.

    Do đó, hai góc hBg và gBf kề nhau.

    - Hai góc gBf và eBf có chung đỉnh B, chung cạnh Bf và hai cạnh Bg và Be nằm về hai phía của đường thẳng chứa Bf.

    Do đó, hai góc gBf và eBf kề nhau.

    - Hai góc hBg và gBe có chung đỉnh B, chung cạnh Bg và hai cạnh Be và Bh nằm về hai phía của đường thẳng chứa Bg.

    Do đó, hai góc hBg và gBe kề nhau.

    - Hai góc eBf và hBf có chung đỉnh B, chung cạnh Bf và hai cạnh Be và Bh nằm về hai phía của đường thẳng chứa Bf.

    Do đó, hai góc eBf và hBf kề nhau.

    Vậy trong hình 18a: hai góc iAj và jAk kề nhau;

    Trong hình 18b: hai góc hBg và gBf kề nhau, hai góc gBf và eBf kề nhau, hai góc hBg và gBe kề nhau, hai góc eBf và hBf kề nhau.

    b) Xét Hình 19:

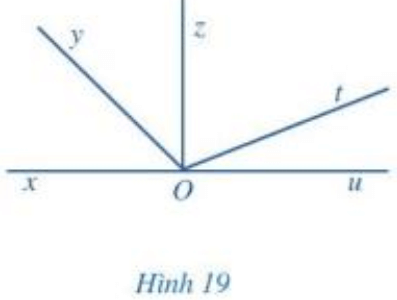
    Tìm hai góc kề nhau trong mỗi hình 18a, 18b

    - Góc xOy và góc yOu là hai góc kề nhau và xOy^+yOu^=xOu^=180o.

    Nên hai góc xOy và yOu là hai góc kề bù.

    - Góc xOz và góc zOu là hai góc kề nhau và xOz^+zOu^=xOu^=180o.

    Nên hai góc xOz và zOu là hai góc kề bù.

    - Góc xOt và góc tOu là hai góc kề nhau và xOt^+tOu^=xOu^=180o.

    Nên hai góc xOt và tOu là hai góc kề bù.

    Vậy trong Hình 19 góc xOy và góc yOu, góc xOz và góc zOu, góc xOt và góc tOu là những cặp góc kề bù.

    c) Xét hình 20a:

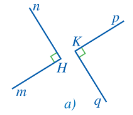
    Toán 7 Bài 1: Góc ở vị trí đặc biệt- Cánh diều (ảnh 1)

    Ta thấy: Mỗi cạnh của góc mHn không phải là cạnh đối của góc pKq.

    Do đó, góc mHn và góc pKq không đối đỉnh.

    - Xét Hình 20b:

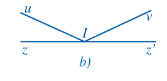
    Toán 7 Bài 1: Góc ở vị trí đặc biệt- Cánh diều (ảnh 1)

    Cạnh Iz của góc zIu và cạnh Iz’ của góc z’Iv đối nhau nhưng cạnh Iu của góc zIu và cạnh Iv của góc z’Iv không đối nhau.

     Do đó, góc zIu và z’Iv không đối đỉnh.

    - Xét Hình 20c:

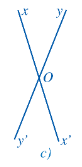
    Toán 7 Bài 1: Góc ở vị trí đặc biệt- Cánh diều (ảnh 1)

    + Cạnh Ox của góc xOy và cạnh Ox’ của góc x’Oy’ đối nhau và cạnh Oy của góc xOy và cạnh Oy’ của góc x’Oy’ đối nhau.

    Nên hai góc xOy và góc x’Oy’ đối đỉnh.

    + Cạnh Ox của góc xOy’ và cạnh Ox’ của góc x’Oy đối nhau và cạnh Oy’ của góc xOy’ và cạnh Oy của góc x’Oy đối nhau.

    Nên hai góc xOy’ và góc x’Oy đối đỉnh.

    - Xét Hình 20d:

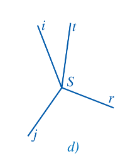
    Toán 7 Bài 1: Góc ở vị trí đặc biệt- Cánh diều (ảnh 1)

    Mỗi tia Si; St; Sr; Sj đều không có tia đối nào trong hình nên Hình 20d không có cặp góc nào đối đỉnh.

    Vậy hai góc đối đỉnh trong Hình 20c là góc xOy và góc x’Oy’, góc xOy’ và góc x’Oy còn các Hình 20a, 20b, và 20d không có cặp góc đối đỉnh.

    Xem thêm lời giải bài tập Toán lớp 7 Cánh diều hay, chi tiết khác: 

    Giải Toán 7 trang 90 Tập 1

    Giải Toán 7 trang 91 Tập 1

    Giải Toán 7 trang 92 Tập 1

    Giải Toán 7 trang 93 Tập 1

    Giải Toán 7 trang 94 Tập 1

    Giải Toán 7 trang 95 Tập 1

    Xem thêm lời giải bài tập Toán lớp 7 Cánh diều hay, chi tiết khác: 

    Bài tập ôn tập chương 3

    Bài 1: Góc ở vị trí đặc biệt

    Bài 2: Tia phân giác của một góc

    Bài 3: Hai đường thẳng song song

    Bài 4: Định lý

    Tham khảo các loạt bài Toán 7 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 467 15/01/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: