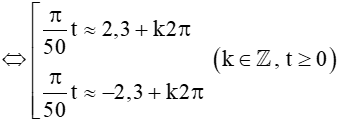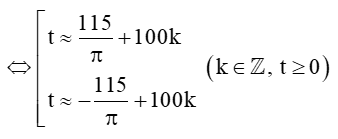Giải Toán 11 trang 32 Tập 1 Cánh diều
Với giải bài tập Toán 11 trang 32 Tập 1 trong Bài 4: Phương trình lượng giác cơ bản sách Cánh diều hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 11 trang 32 Tập 1.
Giải Toán 11 trang 32 Tập 1
Lời giải:
Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:
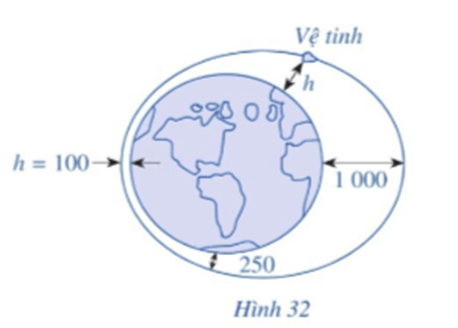
• Để vệ tinh cách mặt đất 1 000 km thì 550 + 450cost = 1 000
450cost=450
cost = 1
t = k2 (k, t0)
t = k2. = 100k (k{0; 1; 2; 3;...}
Vậy tại các thời điểm t = 100k (với k ∈ ℤ, t ≥ 0) (phút) kể từ lúc vệ tinh bay vào quỹ đạo thì vệ tinh cách mặt đất 1 000 km.
• Để vệ tinh cách mặt đất 250 km thì 550 + 450cost = 250
450cost = -300
cost = -
(Dùng máy tính cầm tay (chuyển về chế độ “radian”) bấm liên tiếp 
Vậy tại các thời điểm t +100k (với k ∈ ℤ, t ≥ 0) (phút) kể từ lúc vệ tinh bay vào quỹ đạo thì vệ tinh cách mặt đất 250 km.
• Để vệ tinh cách mặt đất 100 km thì 550 + 450cost = 100
450cost = -450
cost = -1
t = +k2 (kZ, t0).
t = 50+100k (k{0;1;2;3;...}
Vậy tại các thời điểm t = 50 + 100k (với k ∈ ℤ, t ≥ 0) (phút) kể từ lúc vệ tinh bay vào quỹ đạo thì vệ tinh cách mặt đất 100 km.
I. Phương trình tương đương
Hoạt động 1 trang 32 Toán 11 Tập 1: Cho hai phương trình (với cùng ẩn x):
a) Tìm tập nghiệm S1 của phương trình (1) và tập nghiệm S2 của phương trình (2).
b) Hai tập S1, S2 có bằng nhau hay không?
Lời giải:
a) Ta có:
x2 ‒ 3x + 2 = 0 (1)
Suy ra x = 1 hoặc x = 2.
Vậy phương trình (1) có tập nghiệm S1 = {1; 2}.
(x – 1)(x – 2) = 0 (2)
Suy ra x = 1 hoặc x = 2.
Vậy phương trình (2) có tập nghiệm S2 = {1; 2}.
b) Hai tập S1, S2 bằng nhau vì cùng là tập {1; 2}.
Luyện tập 1 trang 32 Toán 11 Tập 1: Hai phương trình x – 1 = 0 và =0 có tương đương không? Vì sao?
Lời giải:
Tập nghiệm của phương trình x – 1 = 0 là S1 = {1}.
Tập nghiệm của phương trình là S2 = {1}.
Vì S1 = S2 nên hai phương trình x – 1 = 0 và =0 tương đương.
Xem thêm lời giải bài tập Toán 11 Cánh diều hay, chi tiết khác:
Xem thêm lời giải bài tập Toán 11 Cánh diều hay, chi tiết khác:
Hoạt động 1 trang 32 Toán 11 Tập 1: Cho hai phương trình (với cùng ẩn x): x2 ‒ 3x + 2 = 0 (1)...
Luyện tập 1 trang 32 Toán 11 Tập 1: Hai phương trình x – 1 = 0 và =0 có tương đương không? Vì sao...
Hoạt động 2 trang 33 Toán 11 Tập 1: Khẳng định 3x ‒ 6 = 0 3x = 6 đúng hay sai...
Luyện tập 2 trang 33 Toán 11 Tập 1: Giải phương trình: (x – 1)2 = 5x – 11...
Luyện tập 3 trang 34 Toán 11 Tập 1: a) Giải phương trình: sin x = ; b) Tìm góc lượng giác x sao cho sinx = sin55°...
Luyện tập 4 trang 35 Toán 11 Tập 1: Giải phương trình sin2x = sin...
Luyện tập 5 trang 36 Toán 11 Tập 1: a) Giải phương trình: cosx = -. b) Tìm góc lượng giác x sao cho cosx = cos(‒87°)...
Luyện tập 6 trang 37 Toán 11 Tập 1: Giải phương trình được nêu trong bài toán mở đầu...
Luyện tập 7 trang 37 Toán 11 Tập 1: a) Giải phương trình: tanx = 1. b) Tìm góc lượng giác x sao cho tanx = tan67°...
Luyện tập 8 trang 39 Toán 11 Tập 1: a) Giải phương trình: cotx = 1. b) Tìm góc lượng giác x sao cho cotx = cot(‒83°)...
Bài 1 trang 40 Toán 11 Tập 1: Giải phương trình: a) sin;...
Bài 2 trang 40 Toán 11 Tập 1: Giải phương trình: a) sin = sinx;...
Bài 3 trang 40 Toán 11 Tập 1: Dùng đồ thị hàm số y = sinx, y = cosx để xác định số nghiệm của phương trình: a) 3sinx + 2 = 0 trên khoảng ;...
Xem thêm lời giải bài tập Toán 11 Cánh diều hay, chi tiết khác:
Bài 3: Hàm số lượng giác và đồ thị
Xem thêm các chương trình khác:
- Soạn văn lớp 11 Cánh diều (hay nhất)
- Văn mẫu lớp 11 - Cánh diều
- Tóm tắt tác phẩm Ngữ văn 11 – Cánh diều
- Tác giả tác phẩm Ngữ văn 11 - Cánh diều
- Giải SBT Ngữ văn 11 – Cánh diều
- Bố cục tác phẩm Ngữ văn 11 – Cánh diều
- Giải Chuyên đề học tập Ngữ văn 11 – Cánh diều
- Nội dung chính tác phẩm Ngữ văn lớp 11 – Cánh diều
- Soạn văn 11 Cánh diều (ngắn nhất)
- Giải sgk Tiếng Anh 11 – ilearn Smart World
- Giải sbt Tiếng Anh 11 - ilearn Smart World
- Trọn bộ Từ vựng Tiếng Anh 11 ilearn Smart World đầy đủ nhất
- Giải sgk Vật lí 11 – Cánh diều
- Lý thuyết Vật lí 11 – Cánh diều
- Giải sbt Vật lí 11 – Cánh diều
- Giải Chuyên đề học tập Vật lí 11 – Cánh diều
- Giải sgk Hóa học 11 – Cánh diều
- Giải Chuyên đề học tập Hóa học 11 – Cánh diều
- Lý thuyết Hóa 11 - Cánh diều
- Giải sbt Hóa học 11 – Cánh diều
- Giải sgk Sinh học 11 – Cánh diều
- Lý thuyết Sinh học 11 – Cánh diều
- Giải Chuyên đề học tập Sinh học 11 – Cánh diều
- Giải sbt Sinh học 11 – Cánh diều
- Giải sgk Giáo dục Kinh tế và Pháp luật 11 – Cánh diều
- Giải Chuyên đề học tập Kinh tế pháp luật 11 – Cánh diều
- Lý thuyết Kinh tế pháp luật 11 – Cánh diều
- Giải sbt Kinh tế pháp luật 11 – Cánh diều
- Giải sgk Lịch sử 11 – Cánh diều
- Giải Chuyên đề học tập Lịch sử 11 – Cánh diều
- Lý thuyết Lịch sử 11 - Cánh diều
- Giải sbt Lịch sử 11 – Cánh diều
- Giải sgk Địa lí 11 – Cánh diều
- Giải Chuyên đề học tập Địa lí 11 – Cánh diều
- Lý thuyết Địa lí 11 - Cánh diều
- Giải sbt Địa lí 11 – Cánh diều
- Giải sgk Công nghệ 11 – Cánh diều
- Lý thuyết Công nghệ 11 - Cánh diều
- Giải sbt Công nghệ 11 – Cánh diều
- Giải sgk Tin học 11 – Cánh diều
- Giải Chuyên đề học tập Tin học 11 – Cánh diều
- Lý thuyết Tin học 11 - Cánh diều
- Giải sbt Tin học 11 – Cánh diều
- Giải sgk Giáo dục quốc phòng an ninh 11 – Cánh diều
- Lý thuyết Giáo dục quốc phòng 11 – Cánh diều
- Giải sbt Giáo dục quốc phòng 11 – Cánh diều
- Giải sgk Hoạt động trải nghiệm 11 – Cánh diều