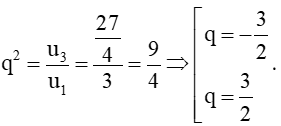Toán 11 Bài 3 (Cánh diều): Cấp số nhân

Giải Toán 11 Bài 3: Cấp số nhân

Giải Toán 11 trang 53 Tập 1

Câu hỏi khởi động trang 53 Toán 11 Tập 1: Vi khuẩn E. coli trong điều kiện nuôi cấy thích hợp cứ 20 phút lại nhân đôi một lần.

(Nguồn: Sinh học 10, NXB Giáo dục Việt Nam, 2010)

Giả sử lúc đầu có 100 vi khuẩn E. coli.

Hỏi có bao nhiêu vi khuẩn E.coli sau 180 phút?

Lời giải:

Số lượng vi khuẩn lúc đầu Q₀ = 100 (vi khuẩn).

Số lượng vi khuẩn sau lần nhân đôi đầu tiên (sau 20 = 1.20 phút) là: Q₁ = 100.2 = 200 (vi khuẩn).

Số lượng vi khuẩn sau lần nhân đôi thứ hai (sau 40 = 2.20 phút) là: Q₂ = 100.2.2 = 100.2² = 400 (vi khuẩn).

Số lượng vi khuẩn sau lần nhân đôi thứ ba (sau 60 = 3.20 phút) là: Q₃ = 100.2.2.2 = 100.2³ = 800 (vi khuẩn).

Tổng quát: Số lượng vi khuẩn sau lần nhân đôi thứ n (sau n. 20 phút) là: Q_n = 100.2ⁿ (vi khuẩn).

Vì vậy số lượng vi khuẩn sau lần nhân đôi thứ thứ 9 (sau 180 = 9.20 phút) là: Q₉ = 100.2⁹ = 51 200 (vi khuẩn).

I. Định nghĩa

Hoạt động 1 trang 53 Toán 11 Tập 1:Cho dãy số$\frac{1}{3}$; 1; 3; 9; 27; 81; 243. Kể từ số hạng thứ hai, nêu mối liên hệ của mỗi số hạng với số hạng đứng ngay trước nó.

Lời giải:

Ta có số hạng thứ hai gấp số hạng đứng trước nó 1:$\frac{1}{3}$=3 lần.

Số hạng thứ ba gấp số hạng đứng trước nó 3:1 = 3 lần.

Số hạng thứ tư gấp số hạng đứng trước nó 9:3 = 3 lần.

Số hạng thứ năm gấp số hạng đứng trước nó 27:9 = 3 lần.

Số hạng thứ sáu gấp số hạng đứng trước nó 81: 27 = 3 lần.

Số hạng thứ bảy gấp số hạng đứng trước nó 243:81 = 3 lần.

Vì vậy ta có kết luận kể từ số hạng thứ hai, ta thấy số hạng sau gấp 3 lần số hạng đứng trước nó.

Luyện tập 1 trang 53 Toán 11 Tập 1: Cho cấp số nhân (u_n) với u₁ = – 6, u₂ = – 2.

a) Tìm công bội q.

b) Viết năm số hạng đầu của cấp số nhân đó.

Lời giải:

a) (u_n) là cấp số nhân có công bội q = $\frac{u_2}{u_1}=\frac{-2}{-6}=\frac{1}{3}$ .

b) Năm số hạng đầu tiên của dãy cấp số nhân là:

u₁ = – 6, u₂ = – 2; u₃=(-6).${\left(\frac{1}{3}\right)}^2=-\frac{2}{3}$; u₄=(-6).${\left(\frac{1}{3}\right)}^3=-\frac{2}{9}$; u₅=(-6).${\left(\frac{1}{3}\right)}^4=-\frac{2}{27}$.

Giải Toán 11 trang 54 Tập 1

Luyện tập 2 trang 54 Toán 11 Tập 1: Cho dãy số (u_n) với u_n = 3.2ⁿ (n ≥ 1). Dãy (u_n) có là cấp số nhân không? Vì sao?

Lời giải:

Ta có: u_n+1 = 3.2ⁿ⁺¹

$\Rightarrow \frac{u_{n+1}}{u_n}=\frac{{3.2}^{n+1}}{{3.2}^n}$ = 2 với n ≥ 1

Vì vậy dãy (u_n) là cấp số nhân có số hạng đầu u₁ = 6 và công bội q = 2.

II. Số hạng tổng quát

Hoạt động 2 trang 54 Toán 11 Tập 1: Cho cấp số nhân (u_n) có số hạng đầu u₁, công bội q.

a) Viết năm số hạng đầu của cấp số nhân theo u₁ và q.

b) Dự đoán công thức tính u_n theo u₁ và q.

Lời giải:

a) Năm số hạng đầu của cấp số nhân đã cho là: u₁; u₁.q; u₁.q²; u₁q³; u₁q⁴.

b) Dự đoán công thức tính u_n theo u₁ và q là: u_n = u₁q^n-1.

Giải Toán 11 trang 55 Tập 1

Luyện tập 3 trang 55 Toán 11 Tập 1: Bác Linh gửi vào ngân hàng 100 triệu đồng tiền tiết kiệm với hình thức lãi kép, kì hạn 1 năm với lãi suất 6%/năm. Viết công thức tính số tiền (cả gốc lẫn lãi) mà bác Linh có được sau n năm (giả sử lãi suất không thay đổi qua các năm).

Lời giải:

Số tiền ban đầu T₁ = 100 (triệu đồng).

Số tiền sau 1 năm bác Linh thu được là:

T₂ = 100 + 100.6% = 100.(1 + 6%) (triệu đồng).

Số tiền sau 2 năm bác Linh thu được là:

T₃ = 100.(1 + 6%) + 100.(1 + 6%).6% = 100.(1 + 6%)² (triệu đồng).

Số tiền sau 3 năm bác Linh thu được là:

T₄ = 100.(1 + 6%)² + 100.(1 + 6%)².6% = 100.(1 + 6%)³ (triệu đồng).

Số tiền sau n năm bác Linh thu được chính là một cấp số nhân với số hạng đầu T₁ = 100 và công bội q = 1 + 6% có số hạng tổng quát là:

T_{n + 1} = 100.(1 + 6%)ⁿ (triệu đồng).

III. Tổng n số hạng đầu của một cấp số nhân

Hoạt động 3 trang 55 Toán 11 Tập 1: Cho cấp số nhân (u_n) có số hạng đầu u₁, công bội q ≠ 1. Đặt S_n = u₁ + u₂ + u₃ + ... + u_n = u₁ + u₁q + u₁q² + ... + u₁q^n-1.

a) Tính S_n.q và S_n – S_n.q.

b) Từ đó, hãy tìm công thức tính S_n theo u₁ và q.

Lời giải:

a) Ta có: S_n.q = (u₁ + u₁q + u₁q² + ... + u₁q^n-1).q

= u₁.q + u₁.q² + u₁q³ + ... + u₁qⁿ

S_n – S_n.q = u₁ + u₁q + u₁q² + ... + u₁q^n-1 – (u₁.q + u₁.q² + u₁q³ + ... + u₁qⁿ)

= u₁ – u₁qⁿ

b) Ta có: $S_n-S_{n}q=u_1-u_1{q}^n$

$\iff S_n\left(1-q\right)=u_1\left(1-q^n\right)$

$\iff S_n=\frac{u_1\left(1-q^n\right)}{1-q}$.

Vậy công thức tính S_n là: $S_n=\frac{u_1\left(1-q^n\right)}{1-q}$ .

Luyện tập 4 trang 55 Toán 11 Tập 1: Tính tổng n số hạng đầu của mỗi cấp số nhân sau:

a) 3; – 6; 12; – 24; ... với n = 12;

b) $\frac{1}{10},\frac{1}{100},\frac{1}{1000}$,... với n = 5.

Lời giải:

a) Ta có: 3; – 6; 12; – 24; ... là cấp số nhân với u₁ = 3 và công bội q = – 2.

Khi đó tổng của 12 số hạng đầu của cấp số nhân đã cho là:

$S_{12}=\frac{3\left(1-{\left(-2\right)}^{12}\right)}{1-\left(-2\right)}$= 12 285.

b) Ta có: $\frac{1}{10},\frac{1}{100},\frac{1}{1000}$,... là một cấp số nhân với u₁ = $\frac{1}{10}$ và công bội q=$\frac{1}{10}$

Khi đó tổng của 5 số hạng đầu của cấp số nhân đã cho là:

$S_5=\frac{\frac{1}{10}\left(1-{\left(\frac{1}{10}\right)}^5\right)}{1-\frac{1}{10}}$= 0,1111.

Bài tập

Giải Toán 11 trang 56 Tập 1

Bài 1 trang 56 Toán 11 Tập 1: Trong các dãy số sau, dãy số nào là cấp số nhân? Vì sao?

a) 5; – 0,5; 0,05; – 0,005; 0,0005;

b) – 9; 3; – 1; $\frac{1}{3};-\frac{1}{9}$;

c) 2; 8; 32; 64; 256.

Lời giải:

a) Từ số hạng thứ hai của dãy số ta thấy số hạng sau gấp -$\frac{1}{10}$ lần số hạng trước của dãy.

Vì vậy dãy trên là cấp số nhân với số hạng đầu u₁ = 5 và công bội q = – 0,5.

b) Từ số hạng thứ hai của dãy số ta thấy số hạng sau gấp -$\frac{1}{3}$ số hạng trước của dãy.

Vì vậy dãy trên là cấp số nhân với số hạng đầu u₁ = – 9 và công bội q= -$\frac{1}{3}$ .

c) Ta có: $\frac{8}{2}=\frac{32}{8}=\frac{256}{64}\ne \frac{64}{32}$

Vì vậy dãy trên không là cấp số nhân.

Bài 2 trang 56 Toán 11 Tập 1: Chứng minh mỗi dãy số (u_n) với mỗi số hạng tổng quát như sau là cấp số nhân:

a) $u_n=-\frac{3}{4}{.2}^n$ ;

b) $u_n=\frac{5}{3^n}$;

c) u_n = ( – 0,75)ⁿ.

Lời giải:

a) Ta có: $u_{n+1}=-\frac{3}{4}{.2}^{n+1}$

Xét $\frac{u_{n+1}}{u_n}=\left(-\frac{3}{4}{.2}^{n+1}\right):\left(-\frac{3}{4}{.2}^n\right)=2$

Vì vậy dãy số đã cho là một cấp số nhân.

b) Ta có: $u_{n+1}=\frac{5}{3^{n+1}}$

Xét $\frac{u_{n+1}}{u_n}=\frac{5}{3^{n+1}}:\frac{5}{3^n}=\frac{1}{3}$.

Vì vậy dãy số đã cho là một cấp số nhân.

c) Ta có: u_n+1 = (– 0,75)ⁿ⁺¹.

Xét $\frac{u_{n+1}}{u_n}={\left(-0,75\right)}^{n+1}:{\left(-0,75\right)}^n=-0,75$.

Vì vậy dãy số đã cho là một cấp số nhân.

Bài 3 trang 56 Toán 11 Tập 1: Cho cấp số nhân (u_n) với số hạng đầu u₁ = – 5, công bội q = 2.

a) Tìm u_n;

b) Số – 320 là số hạng thứ bao nhiêu của cấp số nhân trên?

c) Số 160 có phải là một số hạng của cấp số nhân trên không?

Lời giải:

a) Ta có (u_n) là cấp số nhân có số hạng đầu u₁ = – 5 và công bội q = 2 có số hạng tổng quát là: u_n = – 5.2^n-1 với mọi n ∈ ℕ^*.

b) Xét u_n = – 5.2^n-1 = – 320

⇔ 2^n-1 = 64

⇔ n – 1 = 6

⇔ n = 7.

Vậy số – 320 là số hạng thứ 7 của cấp số nhân.

c) Xét u_n = – 5.2^n-1 = 160

⇔ 2^n-1 = – 32

⇔ n – 1 = – 5

⇔ n = – 4 ∉ ℕ*

Vậy số 160 không phải là một số hạng của cấp số nhân.

Bài 4 trang 56 Toán 11 Tập 1: Cho cấp số nhân (u_n) với u₁ = 3, $u_3=\frac{27}{4}$ .

a) Tìm công bội q và viết năm số hạng đầu của cấp số nhân trên.

b) Tính tổng 10 số hạng đầu của cấp số nhân trên.

Lời giải:

a) Ta có u₃ = u₁.q²

Xét

+) Với q = -$\frac{3}{2}$ ta có năm số hạng đầu của cấp số nhân là:

u₁ = 3, u₂ = 3.$\left(-\frac{3}{2}\right)=-\frac{9}{4}$ ; u₃ = $\frac{27}{4}$; u₄ = 3.${\left(-\frac{3}{2}\right)}^3=-\frac{81}{8}$ ; u₅ = 3.${\left(-\frac{3}{2}\right)}^4=\frac{243}{16}$ .

+) Với q=$\frac{3}{2}$ ta có năm số hạng đầu của cấp số nhân là:

u₁ = 3, u₂ = 3.$\left(\frac{3}{2}\right)=\frac{9}{4}$; u₃ = $\frac{27}{4}$;

u₄ = 3.${\left(\frac{3}{2}\right)}^3=\frac{81}{8}$ ; u₅ = 3.${\left(\frac{3}{2}\right)}^4=\frac{243}{16}$ .

b) Tổng của 10 số hạng đầu của cấp số nhân với số hạng đầu u₁ = 3 và công bội q = -$\frac{3}{2}$ là: $S_{10}=\frac{3\left(1-{\left(-\frac{3}{2}\right)}^{10}\right)}{1-\left(-\frac{3}{2}\right)}\approx$-68.

Tổng của 10 số hạng đầu của cấp số nhân với số hạng đầu u₁ = 3 và công bội q=$\frac{3}{2}$ là: $S_{10}=\frac{3\left(1-{\left(\frac{3}{2}\right)}^{10}\right)}{1-\left(\frac{3}{2}\right)}\approx$340.

Bài 5 trang 56 Toán 11 Tập 1: Một tỉnh có 2 triệu dân vào năm 2020 với tỉ lệ tăng dân số là 1%/năm. Gọi u_n là số dân của tỉnh đó sau n năm. Giải sử tỉ lệ tăng dân số là không đổi.

a) Viết công thức tính số dân của tỉnh đó sau n năm kể từ năm 2020.

b) Tính số dân của tỉnh đó sau 10 năm kể từ năm 2020.

Lời giải:

a) Ta có dãy (u_n) lập thành một cấp số nhân có số hạng đầu là u₀ = 2 triệu dân và công sai q = 1%.

Khi đó số hạng tổng quát của u_n = 2.(1 + 1%)^n-1 (triệu dân).

b) Số dân của tỉnh đó sau 10 năm kể từ năm 2020 là:

u₁₀ = 2.(1 + 1%)^10-1 ≈ 2,19 (triệu dân).

Bài 6 trang 56 Toán 11 Tập 1: Một gia đình mua một chiếc ô tô giá 800 triệu đồng. Trung bình sau mỗi năm sử dụng, giá trị còn lại của ô tô giảm đi 4% (so với năm trước đó).

a) Viết công thức tính giá trị của ô tô sau 1 năm, 2 năm sử dụng.

b) Viết công thức tính giá trị của ô tô sau n năm sử dụng.

c) Sau 10 năm, giá trị của ô tô ước tính còn bao nhiêu triệu đồng?

Lời giải:

a) Sau 1 năm giá trị của ô tô còn lại là:

u₁ = 800 – 800.4% = 800.(1 – 4%) = 768 (triệu đồng).

Sau 2 năm giá trị của ô tô còn lại là:

u₁ = 800.(1 – 4%) – 800.(1 – 4%).4% = 800.(1 – 4%)² = 737,28 (triệu đồng).

b) Gọi u_n là giá trị của ô tô sau n năm sử dụng.

Dãy số (u_n) tạo thành một cấp số nhân với số hạng đầu là giá trị đầu của ô tô là u₀ = 800 triệu đồng và công bội q = 1 – 4%.

Khi đó công thức tổng quát để tính u_n = 800.(1 – 4%)ⁿ.

c) Sau 10 năm sử dụng giá trị của ô tô còn lại là:

u₁₀ = 800.(1 – 4%)¹⁰ ≈ 531,87 (triệu đồng).

Bài 7 trang 56 Toán 11 Tập 1: Một người nhảy bungee (một trò chơi mạo hiểm mà người chơi nhảy từ một nơi có địa thế cao xuống với dây đai an toàn buộc xung quanh người) từ một cây cầu và căng một sợi dây dài 100m. Sau mỗi lần rơi xuống, nhờ sự đàn hồi của dây, người nhảy được kéo lên một quãng đường có độ dài bằng 75% so với lần rơi trước đó và lại bị rơi xuống đúng bằng quãng đường vừa được kéo lên (Hình 3). Tính tổng quãng đường người đó đi được sau 10 lần kéo lên và lại rơi xuống.

Lời giải:

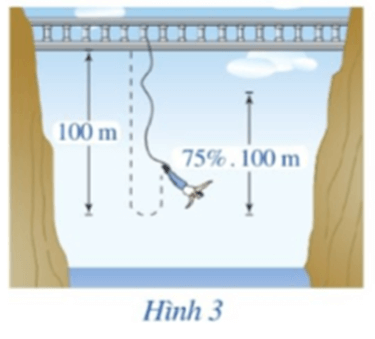
Gọi u_n­ là độ dài dây kéo sau n lần rơi xuống (n ∈ ℕ)

Ta có: u­₀ = 100 (m).

Sau lần rơi đầu tiên độ dài dây kéo còn lại là: u₁ = 100.75% (m).

Sau cú nhảy tiếp theo độ dài dây kéo còn lại là: u₂ = 100.75%.75% = 100.(75%)² (m).

...

Dãy số này lập thành một cấp số nhân có số hạng đầu là 100 và công bội q = 0,75%, có công thức tổng quát u_n = 100.(0,75%)^n-1 (m).

Tổng quãng đường người đó đi được sau 10 lần kéo lên và lại rơi xuống là:

$S_{10}=\frac{100\left(1-{\left(75\%\right)}^{10}\right)}{1-75\%}\approx$377,5 (m).

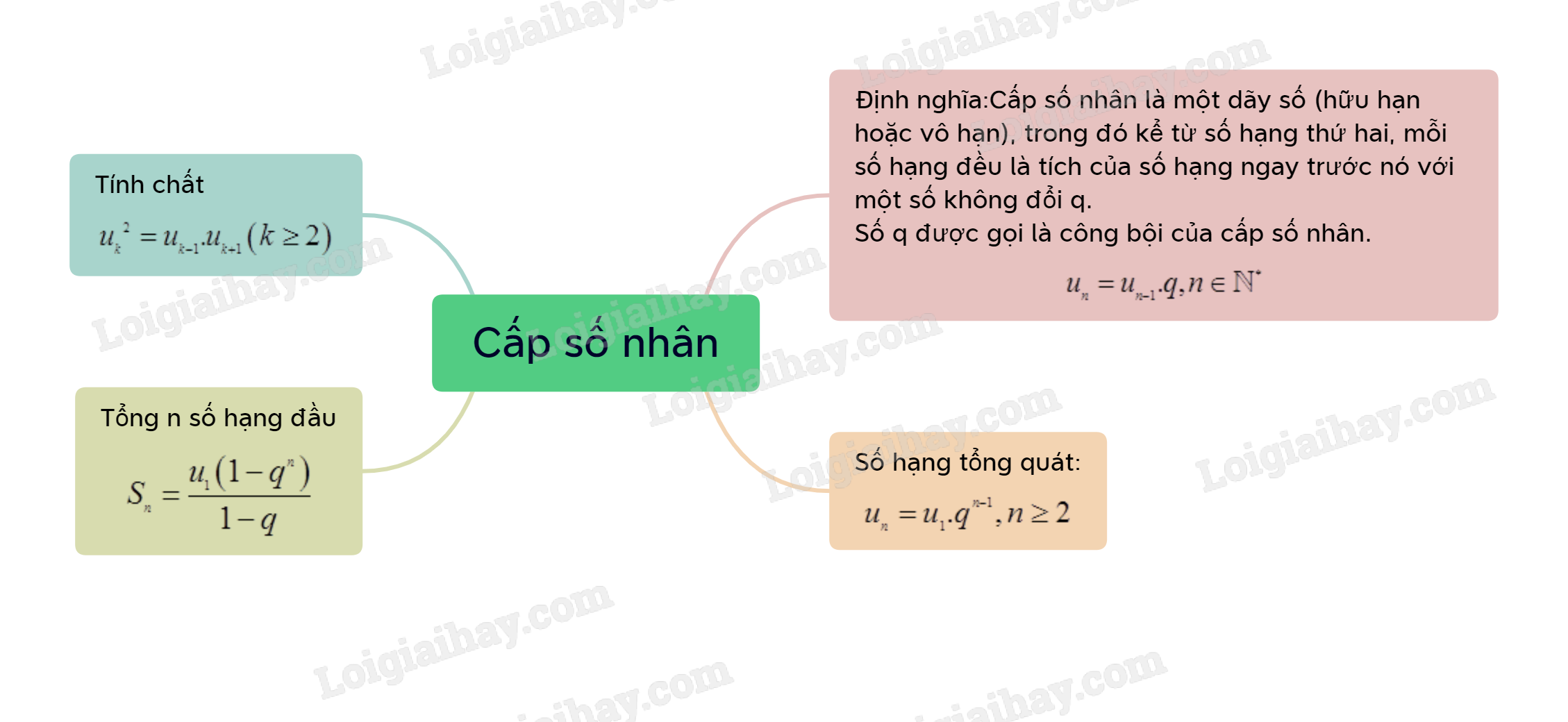
Lý thuyết Cấp số nhân

1. Định nghĩa

Cấp số nhân là một dãy số, trong đó kể từ số hạng thứ hai, mỗi số hạng đều là tích của số hạng ngay trước nó với một số không đổi q. Tức là:

$u_n=u_{n-1}.q,n\in {\mathbb{N}}^{\ast }$

Số q được gọi là công bội của cấp số nhân.

* Chú ý: Dãy $\left(u_n\right)$ là cấp số nhân thì ${u_k}^2=u_{k-1}.u_{k+1}\left(k\ge 2\right)$.

2. Số hạng tổng quát

Nếu một cấp số nhân có số hạng đầu $u_1$ và công bội q thì số hạng tổng quát $u_n$của nó được xác định bởi công thức

$u_n=u_1.q^{n-1},n\ge 2$

3. Tổng của n số hạng đầu của một cấp số nhân

Cho cấp số nhân $\left(u_n\right)$ với công bội $q\ne 1$. Đặt $S_n=u_1+u_2+u_3+...+u_n$. Khi đó

$S_n=\frac{u_1\left(1-q^n\right)}{1-q}$

Xem thêm lời giải bài tập Toán 11 Cánh diều hay, chi tiết khác:

Bài 2: Cấp số cộng

Bài tập cuối chương 2

Bài 1: Giới hạn của dãy số

Bài 2: Giới hạn của hàm số

Bài 3: Hàm số liên tục