Toán 11 Bài 1 (Cánh diều): Dãy số

Giải Toán 11 Bài 1: Dãy số

Giải Toán 11 trang 43 Tập 1

Câu hỏi khởi động trang 43 Toán 11 Tập 1: Một số loài hoa có số lượng cánh hoa luôn là một số cố định. Số cánh hoa trong các bông hoa thường xuất hiện nhiều theo những con số 1, 1, 2, 3, 5, 8, 13, 21,...

Ta có thể viết số cánh hoa của các bông hoa ở các hình trên lần lượt như sau: vị trí thứ nhất viết số 1, vị trí thứ hai viết số 1, vị trí thứ ba viết số 2,..., vị trí thứ tám viết số 21.

Các số 1, 1, 2, 3, 5, 8, 21 được viết theo quy tắc trên gợi nên khái niệm nào trong toán học?

Lời giải:

Các số 1, 1, 2, 3, 5, 8, 21 được viết theo quy tắc trên gợi nên khái niệm “dãy số” trong toán học. Bài học ngày hôm nay sẽ tìm hiểu về khái niệm này.

I. Khái niệm

Hoạt động 1 trang 43 Toán 11 Tập 1: Một vật chuyển động đều với vận tốc 20 m/s. Hãy viết các số chỉ quãng đường (đơn vị: mét) vật chuyển động được lần lượt trong thời gian 1 giây, 2 giây, 3 giây, 4 giây, 5 giây theo hàng ngang.

Lời giải:

Quãng đường vật chuyển động được trong thời gian 1 giây là: 20 . 1 = 20 (m).

Quãng đường vật chuyển động được trong thời gian 2 giây là: 20 . 2 = 40 (m).

Quãng đường vật chuyển động được trong thời gian 3 giây là: 20 . 3 = 60 (m).

Quãng đường vật chuyển động được trong thời gian 4 giây là: 20 . 4 = 80 (m).

Quãng đường vật chuyển động được trong thời gian 5 giây là: 20 . 5 = 100 (m).

Vậy các số chỉ quãng đường (đơn vị: mét) vật chuyển động được lần lượt trong thời gian 1 giây, 2 giây, 3 giây, 4 giây, 5 giây theo hàng ngang là: 20, 40, 60, 80, 100.

Giải Toán 11 trang 44 Tập 1

Luyện tập 1 trang 44 Toán 11 Tập 1: Hàm số u(n) = n³ xác định trên tập hợp M = {1; 2; 3; 4; 5} là một dãy số hữu hạn. Tìm số hạng đầu, số hạng cuối và viết dãy số trên dưới dạng khai triển.

Lời giải:

Số hạng đầu của khai triển là u₁ = u(1) = 1³ = 1.

Số hạng cuối của khai triển là u₅ = u(5) = 5³ = 125.

Dãy số được viết dưới dạng khai triển là: 1; 8; 27; 64; 125.

Hoạt động 2 trang 44 Toán 11 Tập 1: Cho hàm số u(n) = $\frac{1}{n}$, n ∈ ℕ*. Hãy viết các số u₁; u₂; ...; u_n; ... theo hàng ngang.

Lời giải:

Ta có: u₁ = $\frac{1}{1}$ =1; u₂ = $\frac{1}{2}$ ; u₃ = $\frac{1}{3}$ ; ... u_n = $\frac{1}{n}$ ; ...

Luyện tập 2 trang 44 Toán 11 Tập 1: Cho dãy số (u_n) = n².

a) Viết năm số hạng đầu và số hạng tổng quát của dãy số (u_n).

b) Viết dạng khai triển của dãy số (u_n).

Lời giải:

a) Năm số hạng đầu của dãy số là: u­₁ = 1² = 1; u₂ = 2² = 4; u₃ = 3² = 9; u₄ = 4² = 16, u₅ = 5² = 25.

Số hạng tổng quát của dãy số u_n là u_n = n² với n ∈ ℕ.

b) Dạng khai triển của dãy số u₁ = 1; u₂ = 4; u₃ = 9; u₄ = 16, u₅ = 25, ..., u_n = n², ...

II. Cách cho một dãy số

Giải Toán 11 trang 45 Tập 1

Hoạt động 3 trang 45 Toán 11 Tập 1: Xét mỗi dãy số sau:

● Dãy số: 1; 4; 9; 16; 25; 36; 49; 64; 81; 100 (1)

● Cho số $\sqrt{2}$=1,414213562... . Dãy số (u_n) được xác định bởi: Với mỗi số tự nhiên n ≥ 1, u_n là số thập phân hữu hạn có phần số nguyên là 1 và phần thập phân là n chữ số thập phân đầu tiên đứng sau dấu “,” của số $\sqrt{2}$ . Cụ thể là: u₁ = 1,4; u₂ = 1,41; u₃ = 1,414; u₄ = 1,4142; u₅ = 1,41421; ... (2)

● Dãy số (u_n) với (u_n) = (– 2)ⁿ (3)

● Dãy số (u_n) được xác định bởi: u₁ = 1 và u_n = u_n-1 + 2 với mọi n ≥ 2 (4)

a) Hãy nêu cách xác định mỗi số hạng của lần lượt các dãy số (1), (2), (3), (4).

b) Từ đó hãy cho biết dãy số có thể cho bằng những cách nào.

Lời giải:

a) Cách xác định mỗi số hạng của các dãy số đã cho là:

- Dãy số (1) được xác định bằng cách liệt kê.

- Dãy số (2) được xác định bằng cách diễn đạt bằng lời cách xác định mỗi số hạng của dãy số đó.

- Dãy số (3) được xác định bằng cách cho công thức của số hạng tổng quát của dãy số đó.

- Dãy số (4) được xác định bằng cách cho bằng phương pháp quy hồi.

b) Từ ý a) ta có thể thấy dãy số có thể cho bằng 4 phương pháp: liệt kê, diễn đạt bằng lời các xác định mỗi số hạng của dãy số đó, cho công thức của số hạng tổng quát của dãy số đó, cho bằng phương pháp quy hồi.

Giải Toán 11 trang 46 Tập 1

Luyện tập 3 trang 46 Toán 11 Tập 1: Cho dãy số (u_n) với $u_n=\frac{n-3}{3n+1}$ . Tìm u₃₃, u₃₃₃ và viết dãy số dưới dạng khai triển.

Lời giải:

Ta có: $u_3=\frac{3-3}{3.3+1}=0$ ;

$u_{333}=\frac{333-3}{3.333+1}=0,33$.

Dãy số dưới dạng khai triển là:

$u_1=-\frac{1}{2};u_2=-\frac{1}{7};u_3=0,u_4=\frac{1}{13};\mathrm{...};u_n=\frac{n-3}{3.n+1};\mathrm{...}$

III. Dãy số tăng, dãy số giảm

Hoạt động 4 trang 46 Toán 11 Tập 1: Cho dãy số (u_n) với u_n = n². Tính u_n+1. Từ đó, hãy so sánh u_n+1 và u_n với mọi n ∈ ℕ^*.

Lời giải:

Ta có: u_n+1 = (n + 1)² = n² + 2n + 1.

Xét hiệu: u_n+1 – u_n = n² + 2n + 1 – n² = 2n + 1 > 0 với mọi n ∈ ℕ^*.

Vậy u_n+1 > u_n.

Luyện tập 4 trang 46 Toán 11 Tập 1: Chứng minh rằng dãy số (v_n) với v_n = $\frac{1}{3^n}$ là một dãy số giảm.

Lời giải:

Ta có: $u_{n+1}=\frac{1}{3^{n+1}}$

Xét hiệu $u_{n+1}-u_n=\frac{1}{3^{n+1}}-\frac{1}{3^n}=-\frac{2}{3}.\frac{1}{3^n}$<0

Suy ra u_n+1 < u_n.

Vậy dãy số giảm.

IV. Dãy số bị chặn

Giải Toán 11 trang 47 Tập 1

Hoạt động 5 trang 47 Toán 11 Tập 1: Cho dãy số (u_n) với u_n = 1+$\frac{1}{n}$ . Khẳng định u_n ≤ 2 với mọi n ∈ ℕ^* có đúng không?

Lời giải:

Xét hiệu u_n – 2 = 1+$\frac{1}{n}$ - 2 = $\frac{1}{n}$-1

Vì n ∈ ℕ^* nên n ≥ 1 suy ra $\frac{1}{n}$≤ 1 do đó: $\frac{1}{n}$-1≤ 0 .

Vậy u_n – 2 ≤ 0 hay u_n ≤ 2.

Luyện tập 5 trang 47 Toán 11 Tập 1: Chứng minh rằng dãy số (u_n) với $u_n=\frac{n^2+1}{2n^2+4}$ là bị chặn.

Lời giải:

Ta có: $u_n=\frac{n^2+1}{2n^2+4}=\frac{1}{2}\left(\frac{n^2+1}{n^2+2}\right)=\frac{1}{2}\left(1-\frac{1}{n^2+2}\right)<\frac{1}{2}$ .

Ta lại có: $u_n=\frac{n^2+1}{2n^2+4}$>0

Do đó 0<$u_n<\frac{1}{2}$.

Vì vậy dãy số (u_n) bị chặn.

Bài tập

Bài 1 trang 47 Toán 11 Tập 1: Viết năm số hạng đầu của mỗi dãy số có số hạng tổng quát u_n cho bởi công thức sau:

a) u_n = 2n² + 1;

b) u_n = $\frac{{\left(-1\right)}^n}{2n-1}$ ;

c) u_n = $\frac{2^n}{n}$ ;

d) u_n = ${\left(1+\frac{1}{n}\right)}^n$ .

Lời giải:

a) Ta có: 5 số hạng đầu tiên của dãy (u_n) là: u₁ = 2.1² + 1 = 3; u₂ = 2.2² + 1 = 9; u₃ = 2.3² + 1 = 19; u₄ = 2.4² + 1 = 33; u­₅ = 2.5² + 1 = 51.

b) Ta có 5 số hạng đầu của dãy u_n = $\frac{{\left(-1\right)}^n}{2n-1}$ là:

$u_1=\frac{{\left(-1\right)}^1}{2.1-1}=\frac{-1}{1}=-1;$

$u_2=\frac{{\left(-1\right)}^2}{2.2-1}=\frac{1}{3};$

$u_3=\frac{{\left(-1\right)}^3}{2.3-1}=-\frac{1}{5};$

$u_4=\frac{{\left(-1\right)}^4}{2.4-1}=\frac{1}{7};u_5=\frac{{\left(-1\right)}^5}{2.5-1}=-\frac{1}{9}$

c) Ta có 5 số hàng đầu của dãy u_n = $\frac{2^n}{n}$ là:

u₁ = $\frac{2^1}{1}$= 2 ; u₂ = $\frac{2^2}{1}$ =4; u₃ = $\frac{2^3}{1}$= 8 ; u₄ = $\frac{2^4}{1}$ = 16 ; u₅ = $\frac{2^5}{1}$ = 32 .

d) Ta có 5 số hạng đầu của dãy u_n = ${\left(1+\frac{1}{n}\right)}^n$ là:

u₁ = ${\left(1+\frac{1}{1}\right)}^1$ = 2; u₂ = ${\left(1+\frac{1}{2}\right)}^2=\frac{9}{4}$ ; u₃ = ${\left(1+\frac{1}{3}\right)}^3=\frac{64}{27}$ ; u₄ = ${\left(1+\frac{1}{4}\right)}^4=\frac{625}{256}$ ; u₅ = ${\left(1+\frac{1}{5}\right)}^5=\frac{7776}{3125}$.

Bài 2 trang 47 Toán 11 Tập 1: a) Gọi u_n là số chấm ở hàng thứ n trong Hình 1. Dự đoán công thức số hạng tổng quát cho dãy số (u_n).

b) Gọi v_n là tổng diện tích của các hình tô màu ở hàng thứ n trong Hình 2 (mỗi ô vuông nhỏ là một đơn vị diện tích). Dự đoán công thức của số hạng tổng quát cho dãy số (v_n).

Lời giải:

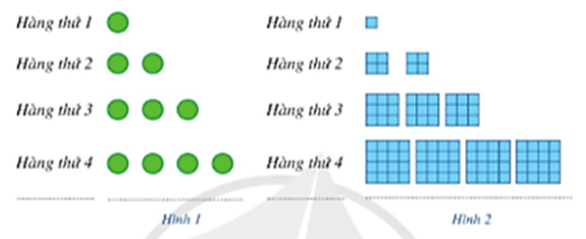
a) Số chấm ở hàng thứ nhất là: u₁ = 1;

Số chấm ở hàng thứ hai là: u₂ = 2;

Số chấm ở hàng thứ ba là: u₃ = 3;

Số chấm ở hàng thứ tư là: u₄ = 4;

Vậy số chấm ở hàng thứ n là: u_n = n.

b) Diện tích của các ô màu ở hàng thứ nhất là: v₁ = 1 = 1³;

Diện tích của các ô màu ở hàng thứ hai là: v₂ = 8 = 2³;

Diện tích của các ô màu ở hàng thứ ba là: v₃ = 27 = 3³;

Diện tích của các ô màu ở hàng thứ tư là: v₄ = 64 = 4³;

Vậy diện tích của các ô màu ở hàng thứ n là: v_n = n³.

Giải Toán 11 trang 48 Tập 1

Bài 3 trang 48 Toán 11 Tập 1: Xét tính tăng, giảm của mỗi dãy số (u_n), biết:

a) $u_n=\frac{n-3}{n+2}$ ;

b) $u_n=\frac{3^n}{2^n.n!}$ ;

c) u_n = (– 1)ⁿ.(2ⁿ + 1).

Lời giải:

a) Ta có: $u_{n+1}=\frac{n+1-3}{n+1+2}=\frac{n-2}{n+3}$

Xét hiệu $u_{n+1}-u_n=\frac{n-2}{n+3}-\frac{n-3}{n+2}$

$=\frac{n^2-4-n^2+9}{\left(n+3\right)\left(n+2\right)}=\frac{5}{\left(n+3\right)\left(n+2\right)}>0,\forall n\in {\mathbb{N}}^{*}$ .

Suy ra u_n+1 > u_n

Vì vậy dãy số đa cho là dãy số tăng.

b) Ta có: $u_{n+1}=\frac{3^{n+1}}{2^{n+1}.\left(n+1\right)!}=\frac{{3.3}^n}{2\left(n+1\right){.2}^n.n!}=\frac{3}{2\left(n+1\right)}.u_n$

Vì n ∈ ℕ^* nên $\frac{3}{2\left(n+1\right)}<\frac{3}{2}$ suy ra u_n+1 < u_n.

Vì vậy dãy số đã cho là dãy số giảm.

c) Ta có: u_n+1 = (– 1)ⁿ⁺¹.(2ⁿ⁺¹ + 1)

+) Nếu n chẵn thì u_n+1 = – (2.2ⁿ + 1) và u_n = 2ⁿ + 1. Do đó u_n+1 < u_n.

Vì vậy với n chẵn thì dãy số đã cho là dãy giảm.

+) Nếu n lẻ thì u_n+1 = 2.2ⁿ + 1 và u_n = – (2ⁿ + 1). Do đó u_n+1 > u_n.

Vì vậy với n chẵn thì dãy số đã cho là dãy tăng.

Bài 4 trang 48 Toán 11 Tập 1: Trong các dãy số (u_n) được xác định như sau, dãy số nào bị chặn dưới, bị chặn trên, bị chặn?

a) u_n = n² + 2;

b) u_n = – 2n + 1;

c) $u_n=\frac{1}{n^2+n}$ .

Lời giải:

a) Ta có: n ∈ ℕ^* nên n ≥ 1 suy ra n² + 2 ≥ 3

Do đó u_n ≥ 3

Vậy dãy số (u_n) bị chặn dưới bởi 3.

b) Ta có: n ∈ ℕ^* nên n ≥ 1 suy ra u_n = – 2n + 1 ≤ – 1

Do đó u_n ≤ – 1.

Vậy dãy số (u_n) bị chặn trên bởi – 1.

c) Ta có: $u_n=\frac{1}{n^2+n}=\frac{1}{n\left(n+1\right)}=\frac{1}{n}-\frac{1}{n+1}$

Vì n ∈ ℕ^* nên n ≥ 1 suy ra $\frac{1}{n}>\frac{1}{n+1}\Rightarrow u_n=\frac{1}{n}-\frac{1}{n+1}$> 0

Ta lại có: $\frac{1}{n}\le$1 và $-\frac{1}{n+1}\le -\frac{1}{2}$ suy ra $u_n=\frac{1}{n}-\frac{1}{n+1}\le 1-\frac{1}{2}=\frac{1}{2}$

Do đó 0<$u_n\le \frac{1}{2}$

Vậy dãy số (u_n) bị chặn.

Bài 5 trang 48 Toán 11 Tập 1: Cho dãy số thực dương (u_n). Chứng minh rằng dãy số (u_n) là dãy số tăng khi và chỉ khi $\frac{u_{n+1}}{u_n}$>1 với mọi n ∈ ℕ^*.

Lời giải:

+) Nếu $\frac{u_{n+1}}{u_n}$>1 với mọi n ∈ ℕ^* thì u_n+1 > u_n. Do đó dãy số (u_n) là dãy số tăng.

+) Nếu (u_n) là dãy số tăng thì u_n+1 > u_n do đó $\frac{u_{n+1}}{u_n}$>1.

Bài 6 trang 48 Toán 11 Tập 1: Chị Mai gửi tiền tiết kiệm vào ngân hàng theo thể thức lãi kép như sau. Lần đầu chị gửi 100 triệu động. Sau đó, cứ hết 1 tháng chị lại gửi thêm vào ngân hàng 6 triệu đồng. Biết lãi suất của ngân hàng là 0,5% một tháng. Gọi P_n (triệu đồng) là số tiền chị có trong ngân hàng sau n tháng.

a) Tính số tiền chị có trong ngân hàng sau 1 tháng.

b) Tính số tiền chị có trong ngân hàng sau 3 tháng.

c) Dự đoán công thức của P_n tính theo n.

Lời giải:

a) Số tiền chị có trong ngân hàng sau 1 tháng là:

P₁ = 100 + 100.0,5% + 6 = 100,5 + 6 (triệu đồng).

b) Số tiền chị có trong ngân hàng sau 2 tháng là:

P₂ = 100,5 + 6 + (100,5 + 6).0,5% + 6= (100,5 + 6)(1 + 0,5%) + 6 = 100,5(1 + 0,5%) + 6.(1 + 0,5%) + 6 (triệu đồng)

Số tiền chị có trong ngân hàng sau 3 tháng là:

P₃ = (100,5 + 6)(1 + 0,5%) + 6 + [(100,5 + 6)(1 + 0,5%) + 6 ].0,5% + 6

= 100,5.(1 + 0,5%)² + 6(1 + 0,5%)² + 6.(1 + 0,5%) + 6 (triệu đồng).

c) Số tiền chị có trong ngân hàng sau 4 tháng là:

P₄ = (100,5 + 6)(1 + 0,5%)² + 6.(1 + 0,5%) + 6 + [(100,5 + 6)(1 + 0,5%)² + 6.(1 + 0,5%) + 6]0,5% + 6

= 100,5.(1 + 0,5%)³ + 6.(1 + 0,5%)³ + 6(1 + 0,5%)² + 6.(1 + 0,5%) + 6

Số tiền chị có trong ngân hàng sau n tháng là:

P_n = 100,5.(1 + 0,5%)^n-1 + 6(1 + 0,5%)^n-1 + 6(1 + 0,5%)^n-2 + 6.(1 + 0,5%)^n-3 + ... + 6 với mọi n ∈ ℕ^*.

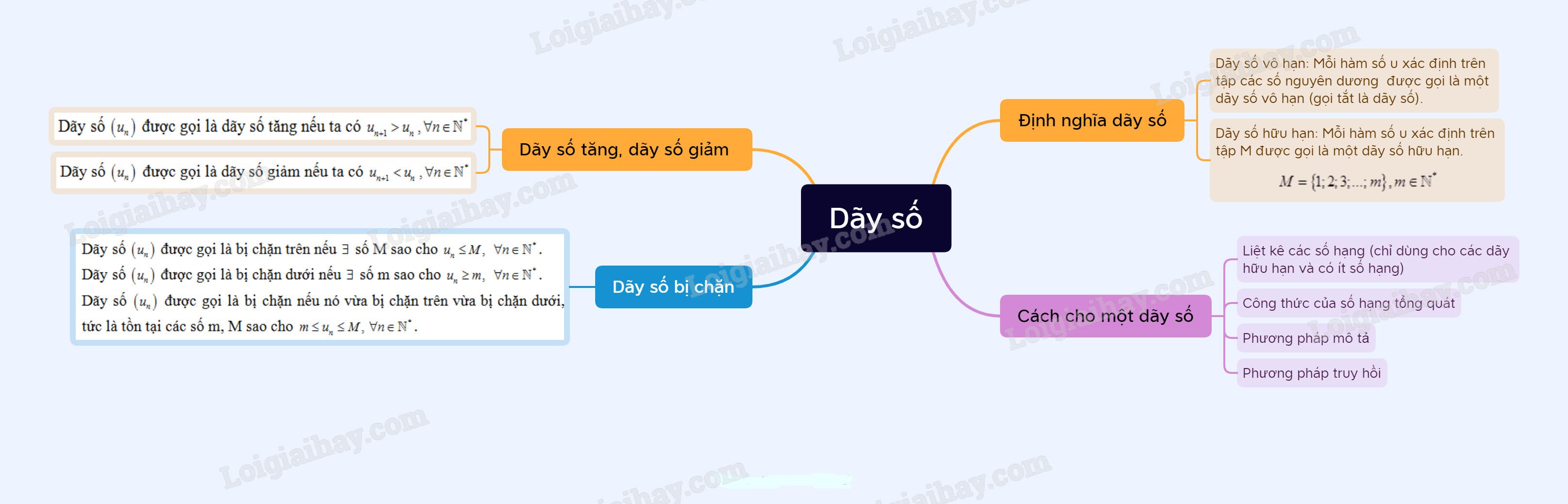
Lý thuyết Dãy số

I. Khái niệm

• Dãy số hữu hạn

Mỗi hàm số u: $\left\{1;2;3;...;m\right\}\to \mathbb{R}\left(m\in {\mathbb{N}}^{\ast }\right)$ được gọi là một dãy số hữu hạn.

Do mỗi số nguyên dương $k\left(1\le k\le m\right)$ tương ứng với đúng một số $u_k$ nên ta có thể viết dãy số đó dưới dạng khai triển: $u_1,u_2,u_3,...,u_m$

Số $u_1$ là số hạng đầu; $u_m$ là số hạng cuối cùng của dãy số đó.

• Dãy số vô hạn

Mỗi hàm số u: ${\mathbb{N}}^{\ast }\to \mathbb{R}$ được gọi là một dãy số vô hạn.

Do mỗi số nguyên dương $n$ tương ứng với đúng một số $u_n$ nên ta có thể viết dãy số đó dưới dạng khai triển: $u_1,u_2,u_3,...,u_n,...$

Số $u_1$ là số hạng đầu; $u_n$ là số hạng thứ n và gọi là số hạng tổng quát của dãy số.

2. Cách cho một dãy số

* Một dãy số có thể cho bằng:

Liệt kê các số hạng (chỉ dùng cho các dãy hữu hạn và có ít số hạng).

Công thức của số hạng tổng quát.

Diễn đạt bằng lời cách xác định mỗi số hạn tổng quát của dãy số đó.

Phương pháp truy hồi.

3. Dãy số tăng, dãy số giảm

Dãy số $\left(u_n\right)$ được gọi là dãy số tăng nếu ta có $u_{n+1}>u_n$$,\mathrm{\forall }n\in {\mathbb{N}}^{\ast }$.

Dãy số $\left(u_n\right)$ được gọi là dãy số giảm nếu ta có $u_{n+1}<u_n$$,\mathrm{\forall }n\in {\mathbb{N}}^{\ast }$.

4. Dãy số bị chặn

Dãy số $\left(u_n\right)$ được gọi là bị chặn trên nếu $\mathrm{\exists }$ số M sao cho $u_n\le M,$ $\mathrm{\forall }n\in {\mathbb{N}}^{\ast }$.

Dãy số $\left(u_n\right)$ được gọi là bị chặn dưới nếu $\mathrm{\exists }$ số m sao cho $u_n\ge m,$ $\mathrm{\forall }n\in {\mathbb{N}}^{\ast }$.

Dãy số $\left(u_n\right)$ được gọi là bị chặn nếu nó vừa bị chặn trên vừa bị chặn dưới, tức là tồn tại các số m, M sao cho $m\le u_n\le M,$$\mathrm{\forall }n\in {\mathbb{N}}^{\ast }$.

Xem thêm lời giải bài tập Toán 11 Cánh diều hay, chi tiết khác:

Bài tập cuối chương 1

Bài 2: Cấp số cộng

Bài 3: Cấp số nhân

Bài tập cuối chương 2

Bài 1: Giới hạn của dãy số