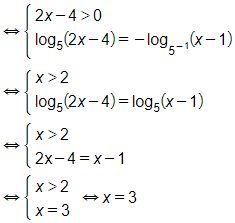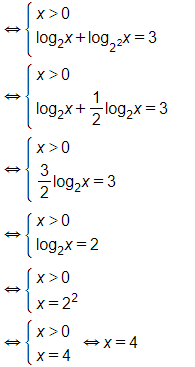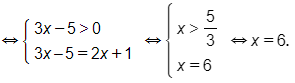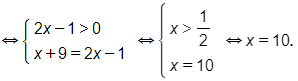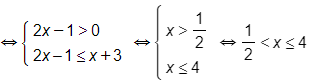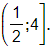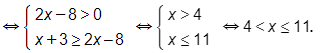Toán 11 Bài 4 (Cánh diều): Phương trình, bất phương trình mũ và lôgarit

Giải Toán 11 Bài 4: Phương trình, bất phương trình mũ và lôgarit

Giải Toán 11 trang 48 Tập 2

Câu hỏi khởi động trang 48 Toán 11 Tập 2: Dân số được ước tính theo công thức S = A . e^rt, trong đó A là dân số của năm lấy làm mốc tính, S là dân số sau t năm, r là tỉ lệ tăng dân số hằng năm.

Hỏi sau bao nhiêu năm, dân số sẽ gấp đôi dân số của năm lấy làm mốc tính?

Lời giải:

Sau bài học này, chúng ta sẽ giải quyết được câu hỏi trên như sau:

Để dân số S’ gấp đôi dân số của năm lấy làm mốc tính S thì S = 2Anên ta có:

Ta có 2A = A . e^rt

Suy ra e^rt = 2

Do đó rt = ln2

Nên $t=\frac{\ln 2}{r}$

Vậy sau $\frac{\ln 2}{r}$ thì dân số sẽ gấp đôi dân số của năm lấy làm mốc tính.

I. Phương trình mũ và phương trình Lôgarit

Hoạt động 1 trang 48 Toán 11 Tập 2: Trong bài toán ở phần mở đầu, giả sử r = 1,14% / năm.

a) Viết phương trình thể hiện dân số sau t năm gấp đôi dân số ban đầu.

b) Phương trình vừa tìm được có ẩn là gì và nằm ở vị trí nào của luỹ thừa?

Lời giải:

a) Ta có công thức S = A . e^rt, trong đó:

⦁ A là dân số của năm lấy làm mốc tính;

⦁ S là dân số sau t năm;

⦁ r là tỉ lệ tăng dân số hằng năm, và r = 1,14%.

Để dân số sau t năm gấp đôi dân số ban đầu thì S = 2A

Suy ra 2A = A . e^1,14%t nên e^0,0114t = 2.

Vậy phương trình thể hiện dân số sau t năm gấp đôi dân số ban đầu là e^0,0114t = 2.

b) Phương trình vừa tìm được có ẩn là t nằm ở số mũ của lũy thừa.

Luyện tập 1 trang 48 Toán 11 Tập 2: Cho hai ví dụ về phương trình mũ.

Lời giải:

Hai ví dụ về phương trình mũ là: 3^x+1 = 9 và 5^2x = 25.

Hoạt động 2 trang 48 Toán 11 Tập 2:

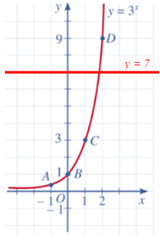
a) Vẽ đồ thị hàm số y = 3^x và đường thẳng y = 7.

b) Nhận xét về số giao điểm của hai đồ thị trên. Từ đó, hãy nêu nhận xét về số nghiệm của phương trình 3^x = 7.

Lời giải:

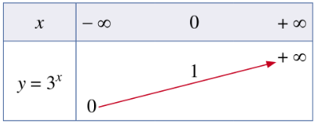
a)⦁ Xét hàm số y = 3^x có cơ số 3 > 1 nên ta có bảng biến thiên như sau:

Đồ thị của hàm số y = 3^x là một đường cong liền nét đi qua các điểm $A\left(-1;\frac{1}{3}\right);B\left(0;1\right);C\left(1;3\right);D\left(2;9\right)$ (hình vẽ).

⦁ Xét hàm số y = 7 có đồ thị là đường thẳng đi qua các điểm có tung độ bằng 7 (hình vẽ).

b) Đồ thị hàm số y = 3^x cắt đường thẳng y = 7 tại 1 điểm.

Vậy phương trình 3^x = 7 có 1 nghiệm.

Giải Toán 11 trang 49 Tập 2

Luyện tập 2 trang 49 Toán 11 Tập 2: Giải mỗi phương trình sau:

a) 9^{16 – x} = 27^{x + 4}; b) 16^{x – 2} = 0,25 . 2^{–x + 4}.

Lời giải:

a) 9^{16 – x} = 27^{x + 4}

⇔3^{2(16 – x)} = 3^{3(x + 4)}

⇔ 2(16 – x) = 3(x + 4)

⇔ 32 – 2x = 3x + 12

⇔ –5x = –20

⇔ x = 4.

Vậy phương trình đã cho có nghiệm là x = 4.

b) 16^{x – 2} = 0,25 . 2^{–x + 4}

⇔2^{4(x – 2)} = 0,25 . 2^{–x + 4}

⇔2^{4(x – 2)}: 2^{–x + 4}= 0,25

$\iff 2^{4x-8+x-4}=\frac{1}{4}$

⇔2^{5x – 12}= 2⁻²

⇔ 5x – 12 = −2

⇔ 5x = 10

⇔ x = 2.

Vậy phương trình đã cho có nghiệm là x = 2.

Hoạt động 3 trang 49 Toán 11 Tập 2: Chỉ số thay đổi pH của một dung dịch được tính theo công thức: pH = – log[H⁺] (trong đó [H⁺] chỉ nồng độ ion hydrogen). Đo chỉ số pH của một số mẫu nước sông, ta có kết quả là pH = 6,1.

a) Viết phương trình thể hiện nồng độ x của hydrogen [H⁺] trong mẫu nước sông đó.

b) Phương trình vừa tìm được có ẩn là gì và nằm ở vị trí nào của lôgarit?

Lời giải:

a) Ta có pH = 6,1 suy ra – log[H⁺] = 6,1 ⇔– logx = 6,1.

Vậy phương trình thể hiện nồng độ x của hydrogen [H⁺] trong mẫu nước sông đó là:

– logx = 6,1.

b) Phương trình vừa tìm được có ẩn x nằm trong biểu thức dưới dấu lôgarit.

Giải Toán 11 trang 50 Tập 2

Luyện tập 3 trang 50 Toán 11 Tập 2: Cho hai ví dụ về phương trình lôgarit.

Lời giải:

Hai ví dụ về phương trình lôgarit là: log₂(x + 3) = 8 và log₃(x² + x + 1) = 2.

Hoạt động 4 trang 50 Toán 11 Tập 2:

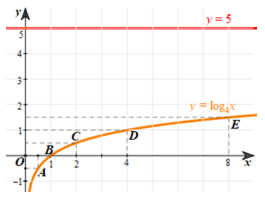
a) Vẽ đồ thị hàm số y = log₄x và đường thẳng y = 5.

b) Nhận xét về số giao điểm của hai đồ thị trên. Từ đó, hãy nêu nhận xét về số nghiệm của phương trình log₄x = 5.

Lời giải:

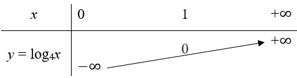
a)⦁ Xét hàm số y = log₄x có cơ số 4 > 1 nên ta có bảng biến thiên như sau:

Đồ thị của hàm số y = log₄x là một đường cong liền nét đi qua các điểm $A\left(\frac{1}{2};-\frac{1}{2}\right);B\left(1;0\right);C\left(2;\frac{1}{2}\right);D\left(4;1\right);E\left(8;\frac{3}{2}\right)$ (hình vẽ).

⦁ Xét hàm số y = 5 có đồ thị là đường thẳng đi qua các điểm có tung độ bằng 5 (hình vẽ).

b) Từ bảng biến thiên của hàm số y = log₄x ta thấy đường thẳng y = 5 cắt đồ thị hàm số y = log₄x tại 1 điểm.

Khi đó phương trình log₄x = 5 có 1 nghiệm.

Giải Toán 11 trang 51 Tập 2

Luyện tập 4 trang 51 Toán 11 Tập 2: Giải mỗi phương trình sau:

a) ${\log }_5\left(2x-4\right)+{\log }_{\frac{1}{5}}\left(x-1\right)=0;$

b) log₂x + log₄x = 3.

Lời giải:

a) ${\log }_5\left(2x-4\right)+{\log }_{\frac{1}{5}}\left(x-1\right)=0$

Vậy phương trình có nghiệm x=3.

b) log₂x + log₄x = 3

Vậy phương trình có nghiệm x=4.

II. Bất phương trình mũ và bất phương trình Lôgarit

Hoạt động 5 trang 51 Toán 11 Tập 2: Quan sát Hình 11 và nêu nhận xét về tính đồng biến, nghịch biến của hàm số $y={\left(\frac{1}{2}\right)}^x.$ Từ đó, hãy tìm x sao cho ${\left(\frac{1}{2}\right)}^x>2.$

Lời giải:

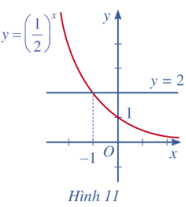
Từ đồ thị hàm số $y={\left(\frac{1}{2}\right)}^x$ở Hình 11 ta thấy hàm số này nghịch biến trên ℝ.

Dựa vào đồ thị ta thấy: đồ thị hàm số $y={\left(\frac{1}{2}\right)}^x$ ở phía trên đường thẳng y = 2 khi và chỉ khi x < −1.

Do đó ${\left(\frac{1}{2}\right)}^x>2\iff x<-1.$

Giải Toán 11 trang 52 Tập 2

Luyện tập 5 trang 52 Toán 11 Tập 2: Cho hai ví dụ về bất phương trình mũ cơ bản.

Lời giải:

Hai ví dụ về bất phương trình mũ cơ bản là 3^x < 27 và 4^x ≥ 16.

Luyện tập 6 trang 52 Toán 11 Tập 2: Giải mỗi bất phương trình sau:

a) 7^x+3 < 343; b) ${\left(\frac{1}{4}\right)}^x\ge 3.$

Lời giải:

Ta có:

a) 7^x+3 < 343

⇔x + 3 < log₇343

⇔x + 3 < 3

⇔x < 0

Vậy tập nghiệm của bất phương trình là (–∞; 0).

b) ${\left(\frac{1}{4}\right)}^x\ge 3$

$\iff x\le {\log }_{\frac{1}{4}}3$

Vậy tập nghiệm của bất phương trình là .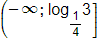

Giải Toán 11 trang 53 Tập 2

Hoạt động 6 trang 53 Toán 11 Tập 2: Quan sát Hình 12 và nêu nhận xét về tính đồng biến, nghịch biến của hàm số lôgarit y = log₂x. Từ đó, hãy tìm x sao cho log₂x > 1.

Lời giải:

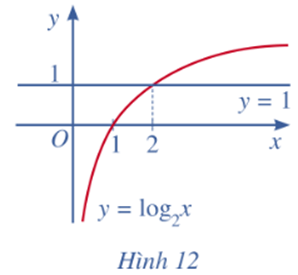
Hàm số y = log₂x đồng biến trên tập xác định (0; +∞).

Dựa vào đồ thị ta thấy đồ thị hàm số y = log₂x ở phía trên đường thẳng y = 1 khi và chỉ khi x > 2.

Vậy log₂x > 1 ⇔ x > 2.

Luyện tập 7 trang 53 Toán 11 Tập 2: Cho hai ví dụ về bất phương trình logarit cơ bản.

Lời giải:

Hai ví dụ về bất phương trình logarit cơ bản là logx > 1 và log₃x≤ 6.

Giải Toán 11 trang 54 Tập 2

Luyện tập 8 trang 54 Toán 11 Tập 2: Giải mỗi bất phương trình sau:

a) log₃x < 2; b) ${\log }_{\frac{1}{4}}\left(x-5\right)\ge -2.$

Lời giải:

a) log₃x < 2

⇔ 0 < x < 3²

⇔ 0 < x < 9

Vậy tập nghiệm của bất phương trình là (0; 9).

b) ${\log }_{\frac{1}{4}}\left(x-5\right)\ge -2$

$\iff 0<x-5\le {\left(\frac{1}{4}\right)}^{-2}$

⇔ 0 < x – 5 ≤ 16

⇔ 5 < x ≤ 21

Vậy tập nghiệm của bất phương trình là (5; 21].

Bài tập

Bài 1 trang 54 Toán 11 Tập 2: Giải mỗi phương trình sau:

a) (0,3)^x–3 = 1; b) 5^3x–2 = 25;

c) 9^x–2 = 243^x+1; d) ${\log }_{\frac{1}{2}}\left(x+1\right)=-3;$

e) log₅(3x – 5) = log₅(2x + 1); g) ${\log }_{\frac{1}{7}}\left(x+9\right)={\log }_{\frac{1}{7}}\left(2x-1\right).$

Lời giải:

a) (0,3)^x–3 = 1⇔ x – 3 = log_0,31 ⇔x – 3 = 0 ⇔x = 3.

Vậy phương trình đã cho có nghiệm là x=3.

b) 5^3x–2 = 25

⇔5^3x–2 = 5²

⇔ 3x – 2 = 2

$\iff x=\frac{4}{3}$

Vậy phương trình đã cho có nghiệm là $x=\frac{4}{3}.$

c) 9^x–2 = 243^x+1⇔3^2x–4 = 3^5x+5

⇔ 2x – 4 = 5x + 5 ⇔ 3x = –9 ⇔ x = –3

Vậy phương trình đã cho có nghiệm là x = –3.

d) ${\log }_{\frac{1}{2}}\left(x+1\right)=-3\iff x+1={\left(\frac{1}{2}\right)}^{-3}\iff x+1=8\iff x=7$

Vậy phương trình đã cho có nghiệm là x=7.

e) log₅(3x – 5) = log₅(2x + 1)

Vậy phương trình đã cho có nghiệm là x=6.

f) $\log \frac{1}{7}\left(x+9\right)=\log \frac{1}{7}\left(2x-1\right)$

Vậy phương trình đã cho có nghiệm là x=10.

Giải Toán 11 trang 55 Tập 2

Bài 2 trang 55 Toán 11 Tập 2: Giải mỗi bất phương trình sau:

a) $3^x>\frac{1}{243};$ b) ${\left(\frac{2}{3}\right)}^{3x-7}\le \frac{3}{2};$

c) 4^x+3 ≥ 32^x; d) log(x – 1) < 0;

e) ${\log }_{\frac{1}{5}}\left(2x-1\right)\ge {\log }_{\frac{1}{5}}\left(x+3\right);$ g) ln(x + 3) ≥ ln(2x – 8).

Lời giải:

a) $3^x>\frac{1}{243}\iff x>{\log }_3\frac{1}{243}\iff x>{\log }_3\frac{1}{3^5}$$\iff x>{\log }_3{3}^{-5}\iff x>-5$

Vậy bất phương trình đã cho có tập nghiệm là (–5; +∞).

b) ${\left(\frac{2}{3}\right)}^{3x-7}\le \frac{3}{2}\iff 3x-7\ge {\log }_{\frac{2}{3}}\frac{3}{2}$

$\iff 3x-7\ge {\log }_{\frac{2}{3}}{\left(\frac{2}{3}\right)}^{-1}\iff 3x-7\ge -1\iff x\ge 2.$

Vậy bất phương trình đã cho có tập nghiệm là [2; +∞).

c) 4^x+3 ≥ 32^x ⇔ x + 3 ≥ log₄32^x ⇔ x + 3 ≥ xlog₄32

$\iff x+3\ge xlo{g}_{2^2}{2}^5\iff x+3\ge x\cdot \frac{1}{2}\cdot 5\cdot lo{g}_{2}2$

$\iff x+3\ge \frac{5}{2}x\iff \frac{-3}{2}x\ge -3\iff x\le 2.$

Vậy bất phương trình đã cho có tập nghiệm là (−∞; 2].

d) log(x – 1) < 0 ⇔0 < x – 1 < 10⁰

⇔0 < x – 1 < 1 ⇔1 < x < 2

Vậy bất phương trình đã cho có tập nghiệm là (1; 2).

e) ${\log }_{\frac{1}{5}}\left(2x-1\right)\ge {\log }_{\frac{1}{5}}\left(x+3\right)$

Vậy bất phương trình đã cho có tập nghiệm là

g) ln(x + 3) ≥ ln(2x – 8)

Vậy bất phương trình đã cho có tập nghiệm là (4; 11].

Bài 3 trang 55 Toán 11 Tập 2: Một người gửi ngân hàng 100 triệu đồng theo hình thức lãi kép có kì hạn là 12 tháng với lãi suất x% / năm (x > 0). Sau 3 năm, người đó rút được cả gốc và lãi là 119,1016 triệu đồng. Tìm x, biết rằng lãi suất không thay đổi qua các năm và người đó không rút tiền ra trong suốt quá trình gửi.

Lời giải:

Công thức tính số tiền rút được (cả gốc và lãi) sau n năm là: 100(1 + x%)ⁿ (triệu đồng).

Sau 3 năm, người đó rút được cả gốc và lãi là 119,1016 triệu đồng nên ta có:

100(1 + x%)³ = 119,1016

$\iff {\left(1+\frac{x}{100}\right)}^3=\mathrm{1,191016}$

$\iff 1+\frac{x}{100}=\sqrt[3]{\mathrm{1,191016}}=\mathrm{1,06}$

$\iff \frac{x}{100}=\mathrm{0,06}\iff x=6$ (thỏa mãn x > 0).

Vậy lãi xuất là 6% / năm.

Bài 4 trang 55 Toán 11 Tập 2: Sử dụng công thức tính mức cường độ âm L ở Ví dụ 14, hãy tính mức cường độ âm mà tai người có thể chịu đựng được, biết rằng giá trị cực đại của mức cường độ âm mà tai người có thể chịu đựng được là 130dB.

Lời giải:

Ta có công thức tính mức cường độ âm L (đơn vị dB) là $L=10\log \frac{I}{{10}^{-12}}$

Do giá trị cực đại của mức cường độ âm mà tai người có thể chịu đựng được là 130dB nên ta có L ≤ 130

$\iff 10\log \frac{I}{{10}^{-12}}\le 130\iff \log \frac{I}{{10}^{-12}}\le 13$

$\iff \frac{I}{{10}^{-12}}\le {10}^{13}\iff I\le {10}^{13}{.10}^{-12}\iff I\le 10$

Vậy cường độ âm mà tai người có thể chịu đựng được là 10 W/m².

Lý thuyết Phương trình mũ, bất phương trình mũ và lôgarit

1. Phương trình mũ

Phương trình mũ cơ bản ẩn x có dạng $a^x=b\left(a>0,a\ne 1\right)$.

- Nếu $b\le 0$ thì phương trình vô nghiệm.

- Nếu $b>0$ thì phương trình có nghiệm duy nhất $x={\log }_{a}b$.

Với $a>0,a\ne 1$ thì

• $a^{f\left(x\right)}=b\iff f\left(x\right)={\log }_{a}b$ với b >0;
• $a^{f\left(x\right)}=a^{g\left(x\right)}\iff f\left(x\right)=g\left(x\right)$.

2. Phương trình lôgarit

Phương trình lôgarit cơ bản ẩn x có dạng ${\log }_{a}x=b\left(a>0,a\ne 1\right)$. Phương trình có nghiệm duy nhất $x=a^b$.

Với $a>0,a\ne 1$ thì

• ${\log }_{a}f\left(x\right)=b\iff f\left(x\right)=a^b$.
• ${\log }_{a}f\left(x\right)={\log }_{a}g\left(x\right)\iff \{\begin{array}{l}f\left(x\right)=g\left(x\right)\\ [\begin{array}{l}f\left(x\right)>0\\ g\left(x\right)>0\end{array}\end{array}$

3. Bất phương trình mũ

Xét bất phương trình mũ $a^x>b\left(a>0,a\ne 1\right)$.

- Nếu $b\le 0$, tập nghiệm của bất phương trình là $\mathbb{R}$;

- Nếu b > 0, a > 1 thì nghiệm của bất phương trình là $x>{\log }_{a}b$;

- Nếu b > 0, 0 < a < 1 thì nghiệm của bất phương trình là $x<{\log }_{a}b$.

Các bất phương trình mũ cơ bản khác được giải tương tự.

4. Bất phương trình lôgarit

Xét bất phương trình lôgarit ${\log }_{a}x>b\left(a>0,a\ne 1\right)$.

- Nếu a > 1 thì nghiệm của bất phương trình là $x>a^b$.

- Nếu 0 < a < 1 thì nghiệm của bất phương trình là 0 < x < $a^b$.

Các bất phương trình lôgarit cơ bản khác được giải tương tự.

Sơ đồ tư duy Phương trình mũ, bất phương trình mũ và lôgarit

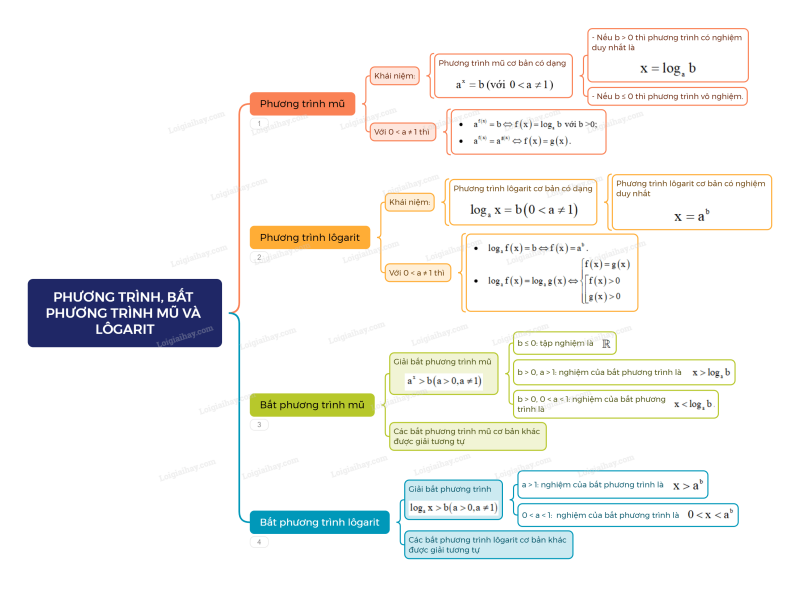
Xem thêm Lời giải bài tập Toán 11 Cánh diều hay, chi tiết khác:

Bài tập cuối chương 5 trang 25

Bài 1: Phép tính lũy thừa với số mũ thực

Bài 2: Phép tính lôgarit

Bài 3: Hàm số mũ. Hàm số lôgarit

Bài tập cuối chương 6 trang 55