Toán 11 Bài 1 (Cánh diều): Định nghĩa đạo hàm. Ý nghĩa hình học của đạo hàm

Giải Toán 11 Bài 1: Định nghĩa đạo hàm. Ý nghĩa hình học của đạo hàm

Giải Toán 11 trang 59 Tập 2

Câu hỏi khởi động trang 59 Toán 11 Tập 2: Tên lửa vũ trụ là phương tiện được chế tạo đặc biệt giúp con người thực hiện các sứ mệnh trong không gian như: tiếp cận đến các hành tinh ngoài Trái Đất, vận chuyển con người và thiết bị lên vũ trụ, ... (Hình 1).

Nếu quỹ đạo chuyển động của tên lửa được miêu tả bằng hàm số theo thời gian thì đại lượng nào biểu thị độ nhanh chậm của chuyển động tại một thời điểm

Lời giải:

Sau bài học này chúng ta sẽ trả lời được câu hỏi trên như sau:

Đại lượng biểu thị tốc độ nhanh chậm của chuyển động tại một thời điểm là v(x0), là đạo hàm của hàm số theo thời gian biểu thị quỹ đạo chuyển động của tên lửa.

I. Đạo hàm tại một điểm

Giải Toán 11 trang 60 Tập 2

Hoạt động 1 trang 60 Toán 11 Tập 2: Tính vận tốc tức thời của viên bi tại thời điểm x0 =1 (s) trong bài toán tìm vận tốc tức thời nêu ở trên

Lời giải:

Ta có vận tốc tức thời tại thời điểm x₀ của viên bi là $v\left(x_0\right)=\underset{x_1\to x_0}{\lim }\frac{f\left(x_1\right)-f \left(x_0\right)}{x_1-x_0}$ với $f\left(x\right)=\frac{1}{2}g{x}^2.$

Vận tốc tức thời của viên bi tại thời điểm x₀ =1 (s) là:

$v\left(x_0\right)=v\left(1\right)=\underset{x_1\to 1}{\lim }\frac{f\left(x_1\right)-f \left(1\right)}{x_1-1}=\underset{x_1\to 1}{\lim }\frac{\frac{1}{2}g{x}_1^2-\frac{1}{2}g\cdot 1^2}{x_1-1}$

$=\underset{x_1\to 1}{\lim }\frac{\frac{1}{2}g\left(x_1^2-1\right)}{x_1-1}=\underset{x_1\to 1}{\lim }\frac{\frac{1}{2}g\left(x_1-1\right)\left(x_1+1\right)}{x_1-1}$

$=\underset{x_1\to 1}{\lim }\frac{1}{2}g\left(x_1+1\right)=\frac{1}{2}g\left(1+1\right)=g\approx 9,8$ (m/s).

Giải Toán 11 trang 61 Tập 2

Luyện tập 1 trang 61 Toán 11 Tập 2: Tính đạo hàm của hàm số $f\left(x\right)=\frac{1}{x}$ tại x₀ = 2 bằng định nghĩa

Lời giải:

⦁ Xét ∆x là số gia của biến số tại điểm x₀ = 2.

Ta có: $\Delta y=f\left(2+\Delta x\right)–f\left(2\right)=\frac{1}{2+\Delta x}-\frac{1}{2}$

$=\frac{2}{2\cdot \left(2+\Delta x\right)}-\frac{2+\Delta x}{2\cdot \left(2+\Delta x\right)}=\frac{-\Delta x}{2\cdot \left(2+\Delta x\right)}$

Suy ra $\frac{\Delta y}{\Delta x}=\frac{\frac{-\Delta x}{2\left(2+\Delta x\right)}}{\Delta x}=-\frac{1}{2\left(2+\Delta x\right)}$

⦁ Ta thấy $\underset{\Delta x\to 0}{\lim }\frac{\Delta y}{\Delta x}=\underset{\Delta x\to 0}{\lim }\frac{-1}{2\left(2+\Delta x\right)}=\frac{-1}{2\left(2+0\right)}=\frac{-1}{4}.$

Vậy $f^{\text{'}}\left(2\right)= \frac{-1}{4}.$

Giải Toán 11 trang 62 Tập 2

Luyện tập 2 trang 62 Toán 11 Tập 2: Tính đạo hàm của hàm số f(x) = x³ tại điểm x bất kì bằng định nghĩa.

Lời giải:

⦁ Xét ∆x là số gia của biến số tại điểm x.

Ta có ∆y = f(x + ∆x) – f(x) = (x + ∆x)³ – x³

= x³ + 3x²∆x + 3x(∆x)² + (∆x)³ – x³

= 3x²∆x + 3x(∆x)² + (∆x)³

= ∆x[3x² + 3x∆x + (∆x)²]

Suy ra $\frac{\Delta y}{\Delta x}=\frac{\Delta x\left[3x^2+3x\Delta x+{\left(\Delta x\right)}^2\right]}{\Delta x}=3x^2+3x\Delta x+{\left(\Delta x\right)}^2.$

⦁ Ta thấy $\underset{\Delta x\to 0}{\lim }\frac{\Delta y}{\Delta x}=\underset{\Delta x\to 0}{\lim }\left[3x^2+3x\cdot \Delta x+{\left(\Delta x\right)}^2\right]=3x^2+3\Delta x\cdot 0+0^2=3x^2.$

Vậy f’(x) = 3x².

II. Ý nghĩa hình học của đạo hàm

Hoạt động 2 trang 62 Toán 11 Tập 2: Cho hàm số y = f(x) có đồ thị (C), một điểm M₀ cố định thuộc (C) có hoành độ x₀. Với mỗi điểm M thuộc (C) khác M₀, kí hiệu x_M là hoành độ của điểm M và k_M là hệ số góc của cát tuyến M₀M. Giả sử tồn tại giới hạn hữu hạn$k_0=\underset{x_M\to x_0}{\lim }{k}_M$ .

Khi đó, ta coi đường thẳng M₀T đi qua M₀ và có hệ số góc k₀ là vị trí giới hạn của cát tuyến M₀M khi điểm M di chuyển dọc theo (C) dần tới M₀.

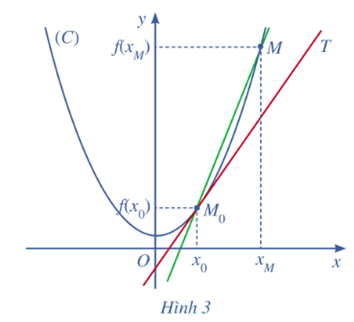
Đường thẳng M₀T được gọi là tiếp tuyến của (C) tại điểm M₀, còn M₀ được gọi là tiếp điểm (Hình 3).

a) Xác định hệ số góc k₀ của tiếp tuyến M₀T theo x₀.

b) Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm M₀

Lời giải:

a)Từ M₀(x₀; y₀) và M(x_M; y_M) ta có $\overrightarrow{M_{0}M}=\left(x_M-x_0;y_M-y_0\right)$

Đường cát tuyến $\overrightarrow{M_{0}M}=\left(x_M-x_0;y_M-y_0\right)$ nhận làm vectơ chỉ phương nên có

Hệ số góc là: $k_M=\frac{y_M-y_0}{x_M-x_0}=\frac{f\left(x_M\right)-f\left(x_0\right)}{x_M-x_0}$

Khi đó: $k_0=\underset{x_M\to x_0}{\lim }{k}_M=\underset{x_M\to x_0}{\lim }\frac{f\left(x_M\right)-f\left(x_0\right)}{x_M-x_0}=f^{\text{'}}\left(x_0\right).$

Vậy k₀ = f’(x₀).

b) Phương trình tiếp tuyến của đồ thị hàm số tại điểm M₀(x₀; y₀) có hệ số góc k₀ = f’(x₀)là:

y = k₀(x – x₀) + y₀ hay y = f’(x₀)(x – x₀) + f(x₀).

Giải Toán 11 trang 63 Tập 2

Luyện tập 3 trang 63 Toán 11 Tập 2: Viết phương trình tiếp tuyến của đồ thị hàm số $y=\frac{1}{x}$tại điểm N(1;1)

Lời giải:

Tiếp tuyến của đồ thị tại điểm có hoành độ bằng 1 có hệ số góc là:

$f^{\text{'}}\left(1\right)=\underset{x\to 1}{\lim }\frac{f\left(x\right)-f\left(1\right)}{x-1}=\underset{x\to 1}{\lim }\frac{\frac{1}{x}-\frac{1}{1}}{x-1}=\underset{x\to 1}{\lim }\frac{\frac{1}{x}-1}{x-1}$

$=\underset{x\to 1}{\lim }\frac{1-x}{x\left(x-1\right)}=\underset{x\to 1}{\lim }\frac{-1}{x}=\frac{-1}{1}=-1.$

Phương trình tiếp tuyến của đồ thị tại điểm N(1; 1) là:

y = –1(x – 1) + 1 hay y = –x + 2

Bài tập

Bài 1 trang 63 Toán 11 Tập 2 :Tính đạo hàm của hàm số f(x) = 3x³ – 1 tại điểm x₀ = 1 bằng định nghĩa:

Lời giải:

Xét ∆x là số gia của biến số tại điểm x₀ = 1.

Ta có ∆y = f(1 + ∆x) – f(1) = 3(1 + ∆x)³ – 1 – (3.1³ – 1)

= 3 + 9∆x + 9.(∆x)² + 3(∆x)³ – 1 – 2

= 9∆x + 9.(∆x)² + 3(∆x)³

= ∆x[9 + 9∆x + 3(∆x)²].

Suy ra: $\frac{\Delta y}{\Delta x}=\frac{\Delta x\left[9+9\Delta x+3{\left(\Delta x\right)}^2\right]}{\Delta x}=9+9\Delta x+3{\left(\Delta x\right)}^2.$

⦁ Ta thấy: $\underset{\Delta x\to 0}{\lim }\frac{\Delta y}{\Delta x}=\underset{\Delta x\to 0}{\lim }\left[9+9\Delta x+3{\left(\Delta x\right)}^2\right]=9+9\cdot 0+3\cdot 0^2=9.$

Bài 2 trang 63 Toán 11 Tập 2 :Chứng minh rằng hàm số f(x) = |x| không có đạo hàm tại điểm x₀ = 0, nhưng có đạo hàm tại mọi điểm x ≠ 0

Lời giải:

Xét ∆x là số gia của biến số tại điểm x₀ = 0.

Ta có ∆y = f(0 + ∆x) – f(0) = |∆x| – |0| = |∆x|.

Suy ra $\frac{\Delta y}{\Delta x}=\frac{\left|\Delta x\right|}{\Delta x}.$

Ta thấy $\underset{\Delta x\to 0^{+}}{\lim }\frac{\Delta y}{\Delta x}=\underset{\Delta x\to 0^{+}}{\lim }\frac{\left|\Delta x\right|}{\Delta x}=\underset{\Delta x\to 0^{+}}{\lim }\frac{\Delta x}{\Delta x}=\underset{\Delta x\to 0^{+}}{\lim }1=1$

$\underset{\Delta x\to 0^{-}}{\lim }\frac{\Delta y}{\Delta x}=\underset{\Delta x\to 0^{-}}{\lim }\frac{\left|\Delta x\right|}{\Delta x}=\underset{\Delta x\to 0^{-}}{\lim }\frac{-\Delta x}{\Delta x}=\underset{\Delta x\to 0^{-}}{\lim }\left(-1\right)=-1$

Do đó $\underset{\Delta x\to 0^{+}}{\lim }\frac{\Delta y}{\Delta x}\ne \underset{\Delta x\to 0^{-}}{\lim }\frac{\Delta y}{\Delta x}$ nên không tồn tại $\underset{\Delta x\to 0}{\lim }\frac{\Delta y}{\Delta x}$

Vậy hàm số f(x) = |x| không có đạo hàm tại điểm x₀ = 0.

Ta có hàm số $f\left(x\right)=\left\{\begin{array}{l}xkhix>0\\ 0khix=0\\ -xkhix<0\end{array}\right.$

⦁ Với x > 0 ta có hàm số f(x) = x.

Xét ∆x là số gia của biến số tại điểm x > 0.

Ta có ∆y = f(x + ∆x) – f(x) = (x + ∆x) – x = ∆x.

Suy ra $\frac{\Delta y}{\Delta x}=\frac{\Delta x}{\Delta x}=1$

Ta thấy $\underset{\Delta x\to 0}{\lim }\frac{\Delta y}{\Delta x}=\underset{\Delta x\to 0}{\lim }1=1$

Do đó với x > 0 thì hàm số có đạo hàm f’(x) = 1.

⦁ Với x < 0 ta có hàm số f(x) = –x.

Xét ∆x là số gia của biến số tại điểm x < 0.

Ta có ∆y = f(x + ∆x) – f(x) = – (x + ∆x) + x = –∆x.

Suy ra $\frac{\Delta y}{\Delta x}=\frac{–\Delta x}{\Delta x}=-1$

Ta thấy $\underset{\Delta x\to 0}{\lim }\frac{\Delta y}{\Delta x}=\underset{\Delta x\to 0}{\lim }\left(-1\right)=-1$

Do đó với x < 0 thì hàm số có đạo hàm f’(x) = –1.

Vậy hàm số f(x) = |x| không có đạo hàm tại x₀ = 0, nhưng có đạo hàm tại mọi điểm x ≠ 0.

Bài 3 trang 63 Toán 11 Tập 2 :Cho hàm y = –2x² + x có đồ thị (C).

a) Xác định hệ số góc của tiếp tuyến của đồ thị (C) tại điểm có hoành độ bằng 2.

b) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm M(2; – 6)

Lời giải:

a) Tiếp tuyến của đồ thị (C) tại điểm có hoành độ bằng 2 có hệ số góc là:

$f^{\text{'}}\left(2\right)=\underset{x\to 2}{\lim }\frac{f\left(x\right)-f\left(2\right)}{x-2}=\underset{x\to 2}{\lim }\frac{-2x^2+x-\left(-2\cdot 2^2+2\right)}{x-2}$

$=\underset{x\to 2}{\lim }\frac{-2x^2+x+6}{x-2}=\underset{x\to 2}{\lim }\frac{-\left(x-2\right)\left(2x+3\right)}{x-2}$

$=\underset{x\to 2}{\lim }\left[-\left(2x+3\right)\right]=-\left(2\cdot 2+3\right)=-7.$

Vậy hệ số góc của tiếp tuyến của đồ thị (C) tại điểm có hoành độ bằng 2 là f’(x) = –7.

b) Phương trình tiếp tuyến của đồ thị (C) tại điểm M(2; – 6) là:

y = –7(x – 2) – 6 hay y = –7x + 8.

Bài 4 trang 63 Toán 11 Tập 2 :Giả sử chi phí C (USD) để sản xuất Q máy vô tuyến là C(Q) = Q² + 80Q + 3 500.

a) Ta gọi chi phí biên là chi phí gia tăng để sản xuất thêm 1 sản phẩm từ Q sản phẩm lên Q + 1 sản phẩm. Giả sử chi phí biên được xác định bởi hàm số C’(Q). Tìm hàm chi phí biên.

b) Tìm C’(90) và giải thích ý nghĩa kết quả tìm được

Lời giải:

a) Xét ∆Q là số gia của biến số tại điểm Q.

Ta có ∆C = C(Q + ∆Q) – C(Q)

= (Q + ∆Q)² + 80(Q + ∆Q) + 3 500 – Q² – 80Q – 3 500

= (∆Q)² + 2Q. ∆Q + 80∆Q.

= ∆Q(∆Q + 2Q + 80).

Suy ra $\frac{\Delta C}{\Delta Q}=\frac{\Delta Q\left(\Delta Q+2Q+80\right)}{\Delta Q}=\Delta Q+2Q+80$

Ta thấy $\underset{\Delta Q\to 0}{\lim }\frac{\Delta C}{\Delta Q}=\underset{\Delta Q\to 0}{\lim }\left(\Delta Q+2Q+80\right)=2Q+80$

Vậy hàm chi phí biên là: C’(Q) = 2Q + 80 (USD).

b) Ta có C’(90) = 2 . 90 + 80 = 260 (USD).

Ý nghĩa: Để sản xuất thêm 1 sản phẩm từ 90 lên 91 sản phẩm cần chi phí biên (chi phí gia tăng) là 260 (USD).

Lý thuyết Định nghĩa đạo hàm. Ý nghĩa hình học của đạo hàm

1. Định nghĩa

- Cho hàm số $y=f\left(x\right)$ xác định trên khoảng (a; b) và điểm $x_0\in \left(a;b\right)$.

Nếu tồn tại giới hạn hữu hạn $\underset{x\to x_0}{lim}\frac{f\left(x\right)-f\left(x_0\right)}{x-x_0}$ thì giới hạn đó được gọi là đạo hàm của hàm số $y=f\left(x\right)$ tại $x_0$ và được kí hiệu là $f^{\prime }\left(x_0\right)$ hoặc $y{}_{x_o}^{\prime }$.

- Hàm số $y=f\left(x\right)$ được gọi là có đạo hàm trên khoảng (a; b) nếu nó có đạo hàm tại mọi điểm x trên khoảng đó.

2. Cách tính đạo hàm bằng định nghĩa

Để tính đạo hàm $f^{\prime }\left(x_0\right)$ của hàm số $y=f\left(x\right)$ tại $x_0$, ta lần lượt thực hiện ba bước sau:

Bước 1. Xét $\mathrm{\Delta }x=x-x_0$ là số gia của biến số tại điểm $x_0$.

Tính $\mathrm{\Delta }y=f\left(x_0+\mathrm{\Delta }x\right)-f\left(x_0\right)$.

Bước 2. Rút gọn tỉ số $\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}$.

Bước 3. Tính $\underset{\mathrm{\Delta }x\to 0}{lim}\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}$.

Kết luận: Nếu $\underset{\mathrm{\Delta }x\to 0}{lim}\frac{\mathrm{\Delta }y}{\mathrm{\Delta }x}=a$ thì $f^{\prime }\left(x_0\right)=a$.

3. Ý nghĩa hình học của đạo hàm

- Đạo hàm của hàm số $y=f\left(x\right)$ tại điểm $x_0$ là hệ số góc của tiếp tuyến của đồ thị hàm số đó tại điểm $M_0\left(x_0;f\left(x_0\right)\right)$.

- Phương trình tiếp tuyến của đồ thị hàm số $y=f\left(x\right)$ tại điểm $M_0\left(x_0;f\left(x_0\right)\right)$ là $y=f^{\prime }\left(x_0\right)\left(x-x_0\right)+f\left(x_0\right)$.

Sơ đồ tư duy Định nghĩa đạo hàm. Ý nghĩa hình học của đạo hàm

Xem thêm Lời giải bài tập Toán 11 Cánh diều hay, chi tiết khác:

Bài 2: Các quy tắc tính đạo hàm

Bài 3: Đạo hàm cấp hai

Bài tập cuối chương 7 trang 76

Bài 1: Hai đường thẳng vuông góc

Bài 2: Đường thẳng vuông góc với mặt phẳng