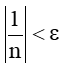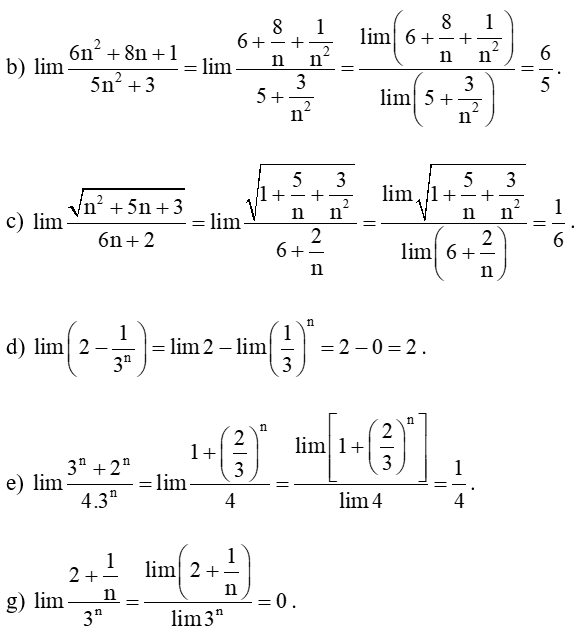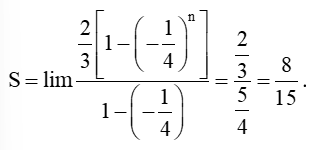Toán 11 Bài 1 (Cánh diều): Giới hạn của dãy số

Giải Toán 11 Bài 1: Giới hạn của dãy số

Bài giảng Toán 11 Bài 1: Giới hạn của dãy số

Giải Toán 11 trang 59 Tập 1

Câu hỏi khởi động trang 59 Toán 11 Tập 1: Zénon (Zê – nông, 496 – 429 trước Công Nguyên) là một triết gia Hy Lạp ở thành phố Edée đã phát biểu nghịch lí như sau: Achilles (A – sin) là một lực sĩ trong thần thoại Hy Lạp, người được mệnh danh là “có đôi chân chạy nhanh như gió” đuổi theo một con rùa trên một đường thẳng. Nếu lúc xuất phát, rùa ở điểm A₁ cách Achilles một khoảng bằng a khác 0. Khi Achilles chạy đến vị trí của rùa xuất phát thì rùa chạy về phía trước một khoảng (như Hình 1). Quá trình này tiếp tục vô hạn. Vì thế, Achilles không bao giờ đuổi kịp rùa.

Trên thực tế, Achilles không đuổi kịp rùa là vô lí. Kiến thức toán học nào có thể giải thích được nghịch lí Zénon nói trên là không đúng?

Lời giải:

Giới hạn hữu hạn của hàm số có thể giải thích được nghịch lí Zénon nói trên là không đúng. Trong bài học ngày hôm nay chúng ta sẽ tìm hiểu về điều đó.

I. Giới hạn hữu hạn của dãy số

Hoạt động 1 trang 59 Toán 11 Tập 1: Hình 2 biểu diễn các số hạng của dãy số (u_n), với u­_n = $\frac{1}{n}$trên hệ trục tọa độ.

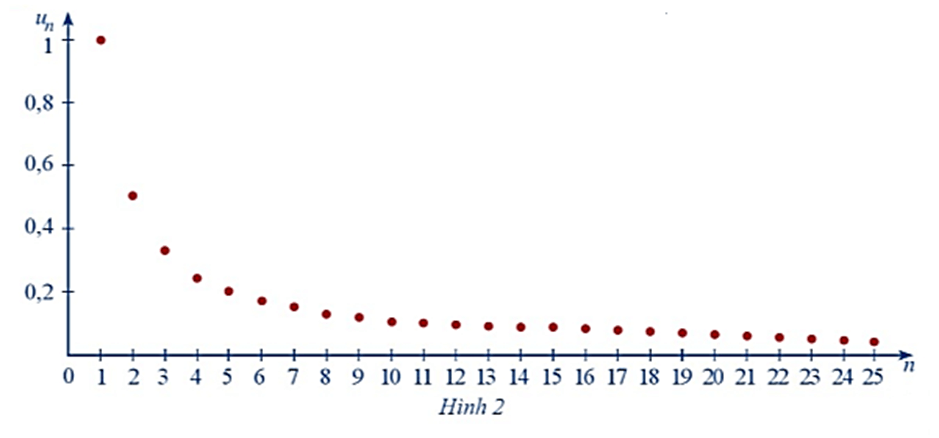
a) Nhận xét về sự thay đổi các giá trị u_n khi n ngày càng lớn.

b) Hoàn thành bảng và trả lời câu hỏi sau:

Kể từ số hạng u_n nào của dãy số thì khoảng cách từ u_n đến 0 nhỏ hơn 0,001? 0,0001?

Lời giải:

a) Khi n ngày càng lớn thì giá trị của u_n càng giảm dần về 0.

b) Ta có bảng:

Kể từ số hạng u₁₀₀₁ trở đi thì khoảng cách từ u_n đến 0 nhỏ hơn 0,001.

Kể từ số hạng u_{10 001} trở đi thì khoảng cách từ u_n đến 0 nhỏ hơn 0,0001.

Giải Toán 11 trang 60 Tập 1

Luyện tập 1 trang 60 Toán 11 Tập 1: Chứng minh rằng:

a) lim 0 = 0;

b) lim$\frac{1}{\sqrt{n}}$=0.

Lời giải:

a) Ta có: u_n = 0 với mọi n ∈ ℕ*

Với mọi ε > 0 bé tùy ý, ta có:

|u_n – 0| < ε với mọi n ∈ ℕ*

Vậy lim 0 = 0.

b) Ta có: u_n = $\frac{1}{\sqrt{n}}$với mọi n ∈ ℕ*

Với mọi ε > 0 bé tùy ý, ta có:

|u_n – 0| < ε ⇔ .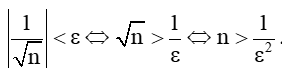

Chọn N ≥ $\frac{1}{{\epsilon }^2}$thì với mọi n >N ta có:

Vì vậy lim$\frac{1}{\sqrt{n}}$=0.

Hoạt động 2 trang 60 Toán 11 Tập 1: Cho dãy số (u_n), với u_n = 2 + $\frac{1}{n}$. Tính $\underset{n\to +\infty }{\lim }\left(u_n-2\right)$.

Lời giải:

Ta có: u_n – 2 = 2 + $\frac{1}{n}$– 2 = $\frac{1}{n}$

Với mọi ε > 0 bé tùy ý, ta có:

|u_n – 0| < ε ⇔ .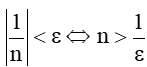

Chọn N ≥ $\frac{1}{\epsilon }$thì với mọi n > N ta có:

Vì vậy lim(u_n-2) = 0.

Giải Toán 11 trang 62 Tập 1

Luyện tập 3 trang 62 Toán 11 Tập 1: Chứng minh rằng: lim${\left(\frac{e}{\pi }\right)}^n$ = 0.

Lời giải:

Ta có $\frac{e}{\pi }$< 1do đó lim${\left(\frac{e}{\pi }\right)}^n$ = 0.

II. Định lí về giới hạn hữu hạn

Hoạt động 3 trang 62 Toán 11 Tập 1: Cho hai dãy số (u_n), (v_n) với u_n = 8+$\frac{1}{n}$; v_n = 4-$\frac{2}{n}$.

a) Tính limu_n, limv_n.

b) Tính lim(u_n + v_n) và so sánh giá trị đó với tổng limu_n + limv_n.

c) Tính lim(u_n.v_n) và so sánh giá trị đó với tổng limu_n.limv_n.

Lời giải:

a) Ta có: lim(u_n-8) = lim$\left(8+\frac{1}{n}-8\right)$ = 0.

Do đó limu_n = 8.

Ta có: lim(v_n-4) = lim$\left(4-\frac{2}{n}-4\right)$ = 0.

Do đó limv_n = 4.

b) limu_n + limv_n = 8 + 4 = 12.

Ta có: u_n + v_n = 8+$\frac{1}{n}$+4-$\frac{2}{n}$ = 12-$\frac{1}{n}$

Ta lại có: lim(u_n+v_n-12) = lim$\left(12-\frac{1}{n}-12\right)$ = 0.

Suy ra lim(u_n + v_n) = 12.

Vì vậy lim(u_n + v_n) = limu_n + limv_n.

b) Ta có: u_n.v_n = $\left(8+\frac{1}{n}\right)\left(4-\frac{2}{n}\right)=32-\frac{12}{n}-\frac{2}{n^2}$.

Khi đó lim(u_n.v_n – 32) = lim$\left(32-\frac{12}{n}-\frac{2}{n^2}-32\right)$=0.

Ta lại có: limu_n.limv_n = 8.4 = 32.

Vì vậy limu_n.limv_n = lim(u_nv_n).

Luyện tập 4 trang 62 Toán 11 Tập 1: Tính các giới hạn sau:

a) lim$\frac{8n^2+n}{n^2}$;

b) lim$\frac{\sqrt{4+n^2}}{n}$.

Lời giải:

a) lim$\frac{8n^2+n}{n^2}=\lim \left(8+\frac{1}{n}\right)=\lim 8+\lim \frac{1}{n}=8$.

b) $\lim \frac{\sqrt{4+n^2}}{n}=\lim \sqrt{\frac{4}{n^2}+1}=\sqrt{\lim \left(\frac{4}{n^2}+1\right)}=1$.

III. Tổng của cấp số nhân lùi vô hạn

Giải Toán 11 trang 63 Tập 1

Hoạt động 4 trang 63 Toán 11 Tập 1: Cho cấp số nhân (u_n), với u₁ = 1 và công bội q=$\frac{1}{2}$.

a) Hãy so sánh |q| với 1.

b) Tính S_n = u₁ + u₂ + ... + u_n. Từ đó, hãy tính limS_n.

Lời giải:

a) Ta có: |q| = $\frac{1}{2}$< 1.

b) Ta có: (u_n) là cấp số nhân lùi vô hạn có tổng n số hạng đầu tiên là:

$S_n=\frac{1.\left(1-{\left(\frac{1}{2}\right)}^n\right)}{1-\frac{1}{2}}=2\left(1-{\left(\frac{1}{2}\right)}^n\right)$

$\lim S_n=\lim 2\left(1-{\left(\frac{1}{2}\right)}^n\right)=\lim 2.\lim \left(1-{\left(\frac{1}{2}\right)}^n\right)=2$.

Luyện tập 5 trang 63 Toán 11 Tập 1: Tính tổng M = 1-$\frac{1}{2}+\frac{1}{2^2}-\mathrm{...}+{\left(-\frac{1}{2}\right)}^{n-1}+\mathrm{...}$

Lời giải:

Ta có dãy số 1; $-\frac{1}{2}$; $\frac{1}{2^2}$; ...; ${\left(-\frac{1}{2}\right)}^{n-1}$; ... là một cấp số nhân lùi vô hạn với số hạng đầu u₁ = 1 và công bội q = $-\frac{1}{2}$ thỏa mãn |q| < 1.

Do đó ta có: $M=1-\frac{1}{2}+\frac{1}{2^2}-\mathrm{...}+{\left(-\frac{1}{2}\right)}^{n-1}+\mathrm{...}=\frac{1}{1-\left(-\frac{1}{2}\right)}=\frac{2}{3}$.

Luyện tập 6 trang 63 Toán 11 Tập 1: Giải thích vì sao nghịch lí Zénon trong phần mở đầu là không đúng.

Lời giải:

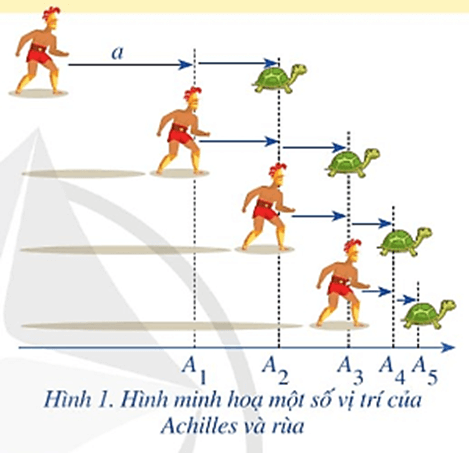
Giả sử vận tốc của Asin gấp đôi vận tốc của chú rùa và khoảng cách lúc đầu là a.

Khi Asin chạy được a thì chú rùa chạy được $\frac{a}{2}$.

Khi Asin chạy tiếp được $\frac{a}{2}$thì chú rùa chạy được $\frac{a}{4}$.

Do đó tổng quãng đường Asin phải chạy để đuổi kịp chú rùa là:

$a+\frac{a}{2}+\frac{a}{4}+\frac{a}{8}+\mathrm{...}$

Theo lập luận của Asin tổng này là tổng vô hạn nên không bao giờ Asin đuổi kịp chú rùa.

Tuy nhiên các số hạng của tổng này lập thành một cấp số nhân với số hạng đầu u₁ = a và công bội q = $\frac{1}{2}$< 1.

Nên ta có tổng của cấp số nhân lùi vô hạn bằng:

$S=a+\frac{a}{2}+\frac{a}{4}+\frac{a}{8}+\mathrm{...}=\lim \frac{a\left(1-{\left(\frac{1}{2}\right)}^n\right)}{1-\frac{1}{2}}=2a$.

Vì vậy tổng này là hữu hạn do đó Asin hoàn toàn có thể chạy để đuổi kịp rùa.

IV. Giới hạn vô cực

Hoạt động 5 trang 63 Toán 11 Tập 1: Quan sát dãy số (u_n) với u­_n = n² và cho biết giá trị của n_n có thể lớn hơn một số dương bất kì được hay không kể từ một số hạng nào đó trở đi.

Lời giải:

Ta có bảng giá trị sau:

Từ đó ta có các nhận xét sau:

+) Kể từ số hạng thứ 2 trở đi thì u_n > 1 .

+) Kể từ số hạng thứ 101 trở đi thì u_n > 10 000.

...

Vậy ta thấy u_n có thể lớn hơn một số dương bất kì kể từ một số hạng nào đó trở đi.

Giải Toán 11 trang 64 Tập 1

Luyện tập 7 trang 64 Toán 11 Tập 1: Tính lim(– n³).

Lời giải:

Xét dãy số (u_n) = n³.

Với M là số dương bất kì, ta thấy u_n = n³ > m ⇔ n > $\sqrt[3]{M}$.

Suy ra với các số tự nhiên n > $\sqrt[3]{M}$thì u_n > M. Do đó limn³ = +∞.

Vậy limn³ = – ∞.

Luyện tập 8 trang 64 Toán 11 Tập 1: Chứng tỏ rằng lim$\frac{n-1}{n^2}$=0.

Lời giải:

Ta có:

Đặt u_n = n – 1 và $v_n=\frac{1}{n^2}$, khi đó limu_n = +∞ và limv_n=lim$\frac{1}{n^2}$=0.

Vậy lim$\frac{n-1}{n^2}$=limu_n.limv_n=0.

Bài tập

Bài 1 trang 64 Toán 11 Tập 1: Cho hai dãy số (u_n), (v_n) với u_n = 3 + $\frac{1}{n}$, v_n = 5 –$\frac{2}{n^2}$. Tính các giới hạn sau:

a) limu_n, limv_n;

b) lim(u_n + v_n), lim(u_n – v_n), lim(u_n.v_n), lim$\frac{u_n}{v_n}$.

Lời giải:

a) Ta có:

limu_n = lim(3 + $\frac{1}{n}$) = lim3 + lim$\frac{1}{n}$= 3 + 0 = 3.

limv_n = lim(5 – $\frac{2}{n^2}$) = lim5 – lim$\frac{2}{n^2}$= 5 – 0 = 5.

b) lim(u_n + v_n) = limu_n + limv_n = 3 + 5 = 8.

lim(u_n – v_n) = limu_n – limv_n = 3 – 5 = – 2.

lim(u_n.v_n) = limu_n.limv_n = 3.5 = 15.

lim$\frac{u_n}{v_n}$= $\frac{\lim u_n}{\lim v_n}=\frac{3}{5}$.

Giải Toán 11 trang 65 Tập 1

Bài 2 trang 65 Toán 11 Tập 1: Tính các giới hạn sau:

a) lim$\frac{5n+1}{2n}$;

b) lim$\frac{6n^2+8n+1}{5n^2+3}$;

c) lim$\frac{\sqrt{n^2+5n+3}}{6n+2}$;

d) lim$\left(2-\frac{1}{3^n}\right)$;

e) lim$\frac{3^n+2^n}{{4.3}^n}$;

g) lim$\frac{2+\frac{1}{n}}{3^n}$.

Lời giải:

a) lim$\frac{5n+1}{2n}$ = lim$\left(\frac{5}{2}+\frac{1}{2n}\right)=\lim \frac{5}{2}+\lim \frac{1}{2n}=\frac{5}{2}$.

Bài 3 trang 65 Toán 11 Tập 1: a) Tính tổng của cấp số nhân lùi vô hạn (u_n­), với u₁=$\frac{2}{3}$, q=-$\frac{1}{4}$.

b) Biểu diễn số thập phân vô hạn tuần hoàn 1,(6) dưới dạng phân số.

Lời giải:

a) Tổng của cấp số nhân lùi vô hạn (u_n), với u₁=$\frac{2}{3}$, q=-$\frac{1}{4}$là:

b) Ta có:

1,(6) = 1 + 0,(6) = 1 + 0,6 + 0,06 + 0,006 + ... + 0,000006 + ...

Dãy số 0,6; 0,006; 0,0006; ... lập thành một cấp số nhân có số hạng đầu u₁ = 0,6 và công bội q = $\frac{1}{10}$có |q| < 1 nên ta có:

0,6 + 0,06 + 0,006 + ... + 0,000006 + ... =$\frac{0,6}{1-\frac{1}{10}}=\frac{2}{3}$.

Suy ra 1,(6) = 1 + $\frac{2}{3}$=$\frac{5}{3}$.

Bài 4 trang 65 Toán 11 Tập 1: Từ hình vuông có độ dài cạnh bằng 1, người ta nối các trung điểm của cạnh hình vuông để tạo ra hình vuông mới như Hình 3. Tiếp tục quá trình này đến vô hạn.

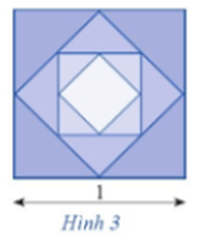
a) Tính diện tích S_n của hình vuông được tạo thành ở bước thứ n;

b) Tính tổng diện tích của tất cả các hình vuông được tạo thành.

Lời giải:

a) Gọi S_n là diện tích của hình vuông thứ n.

Ta có: S₁ = 1; S₂ = $\frac{1}{2}$; S₃ = ${\left(\frac{1}{2}\right)}^2$; ...

Dãy (S_n) lập thành cấp số nhân có số hạng đầu S₁ = 1 và công bội q = $\frac{1}{2}$có công thức tổng quát là: Sn = ${\left(\frac{1}{2}\right)}^{n-1}$.

b) Ta có: |q|=|$\frac{1}{2}$|<1nên dãy (S_n­) trên lập thành một cấp số nhân lùi hạn nên ta có:

S = 1+$\frac{1}{2}+{\left(\frac{1}{2}\right)}^2+{\left(\frac{1}{2}\right)}^3+\mathrm{...}+{\left(\frac{1}{2}\right)}^{n-1}+\mathrm{...}=\frac{1}{1-\frac{1}{2}}=2$.

Vậy tổng diện tích của các hình vuông là 2 (đvdt).

Bài 5 trang 65 Toán 11 Tập 1: Có 1 kg chất phóng xạ độc hại. Biết rằng, cứ sau một khoảng thời gian T = 24 000 năm thì một nửa số chất phóng xạ này bị phân ra thành chất khác không độc hại đối với sức khỏe của con người (T được gọi là chu kì bán rã).

(Nguồn: Đại số và Giải tích 11, NXB GD Việt Nam, 2021).

Gọi u_n là khối lượng chất phóng xạ còn lại sau chu kì thứ n.

a) Tìm số hạng tổng quát u_n của dãy số (u_n).

b) Chứng minh rằng (u_n) có giới hạn là 0.

c) Từ kết quả câu b), chứng tỏ rằng sau một số năm nào đó khối lượng chất phóng xạ đã cho ban đầu không còn độc hại đối với con người, biết rằng chất phóng xạ này sẽ không độc hại nữa nếu khối lượng chất phóng xạ còn bé lại bé hơn 10^{– 6} g.

Lời giải:

a) Ta có: u₁ = 1; u₂ = $\frac{1}{2}$; u₃ = ${\left(\frac{1}{2}\right)}^2$; ...

Suy ra (u_n­) lập thành một cấp số nhân có số hạng đầu u₁ = 1 và q = $\frac{1}{2}$có số hạng tổng quát là: $u_n={\left(\frac{1}{2}\right)}^{n-1}$.

b) Ta có: lim$u_n=\lim {\left(\frac{1}{2}\right)}^{n-1}$=0.

c) Đổi $u_n={\left(\frac{1}{2}\right)}^{n-1}kg={\left(\frac{1}{2}\right)}^{n-1}{.10}^{3}g$

Để chất phóng xạ bé hơn 10^-6 (g) thì ${\left(\frac{1}{2}\right)}^{n-1}{.10}^3<{10}^{-6}\iff$n>31.

Vậy cần ít nhất 30 chu kì tương ứng với 720 000 năm khối lượng chất phóng xạ đã cho ban đầu không còn độc hại đối với con người.

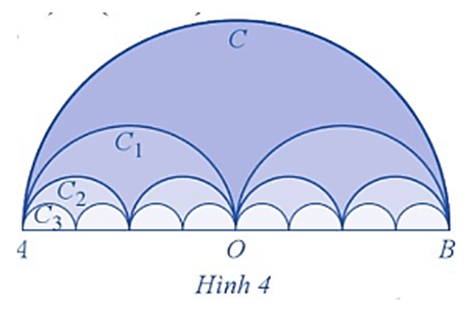
Bài 6 trang 65 Toán 11 Tập 1: Gọi C là nửa đường tròn đường kính AB = 2R.

C₁ là đường gồm hai nửa đường tròn đường kính $\frac{AB}{2}$.

C₂ là đường gồm bốn nửa đường tròn đường kính $\frac{AB}{4}$, ...

C_n là đường gồm 2ⁿ nửa đường tròn đường kính $\frac{AB}{2^n}$,...(Hình 4).

Gọi P_n là độ dài của C_n­, S_n là diện tích hình phẳng giới hạn bởi C_n và đoạn thẳng AB.

a) Tính p_n, S_n.

b) Tìm giới hạn của các dãy số (p_n) và (S_n).

Lời giải:

a)

+) Ta có: p₁ = $\frac{\pi R}{2}$; p₂ = $\frac{\pi R}{4}=\frac{\pi R}{2^2}$; p₃ = $\frac{\pi R}{8}=\frac{\pi R}{2^3}$; ...

(p_n) lập thành một cấp số nhân lùi vô hạn với số hạng đầu p₁ = $\frac{\pi R}{2}$và công bội q = $\frac{1}{2}$<1 có số hạng tổng quát p_n = $\frac{\pi R}{2}.{\left(\frac{1}{2}\right)}^{n-1}$.

+) Ta có: C₁ = $\frac{\pi R^2}{4}$; C₂ = $\frac{\pi R^2}{4^2}$; C₃ = $\frac{\pi R^3}{4^3}$; ...

(C_n) lập thành một cấp số nhân lùi vô hạn với số hạng đầu C₁ = $\frac{\pi R^2}{4}$và công bội q = $\frac{1}{4}$<1có số hạng tổng quát C_n = $\frac{\pi R}{4}.{\left(\frac{1}{4}\right)}^{n-1}$.

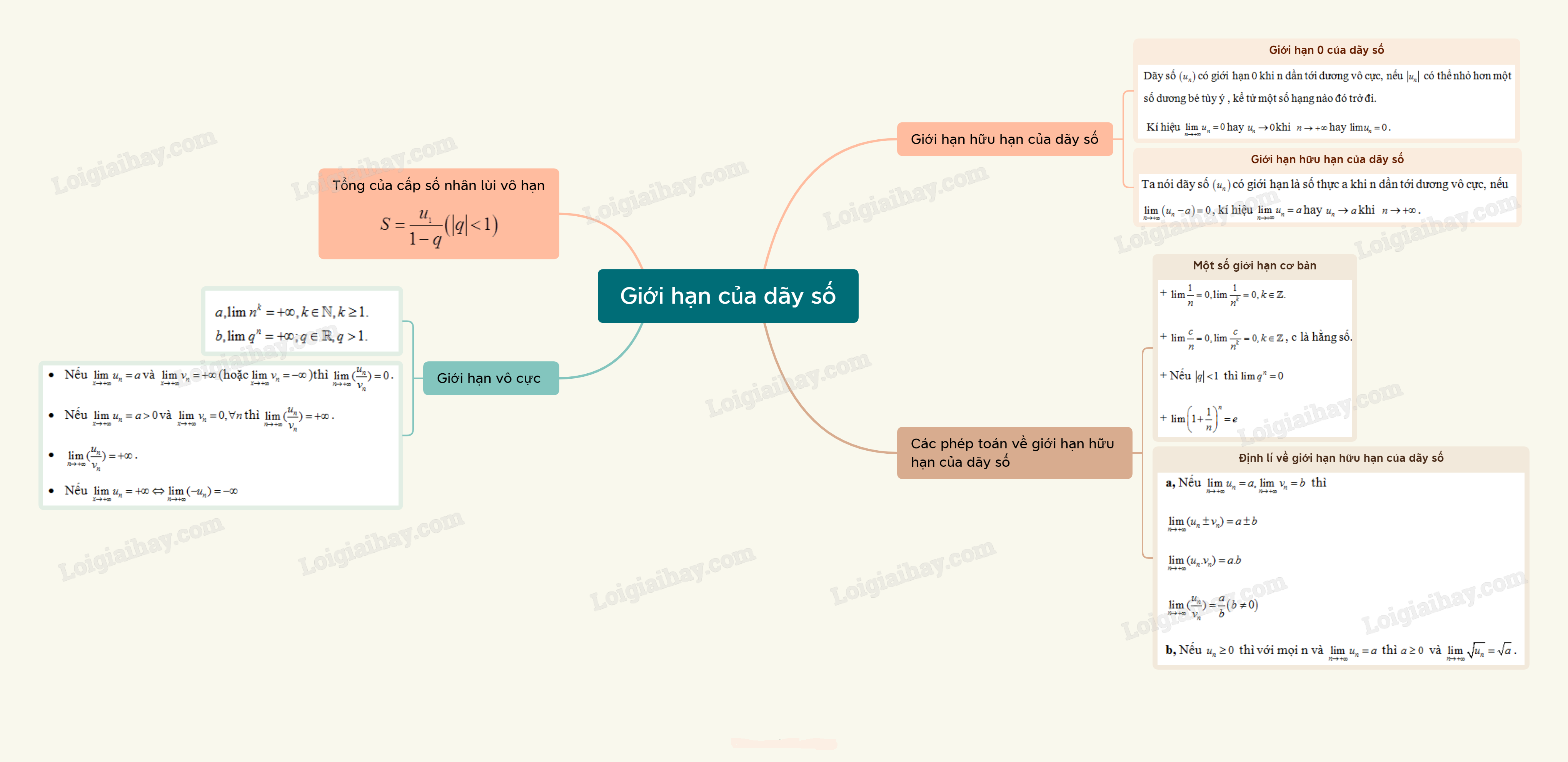
Lý thuyết Giới hạn của dãy số

1. Giới hạn hữu hạn của dãy số

- Dãy số $\left(u_n\right)$ có giới hạn 0 khi n dần tới dương vô cực, nếu $\left|u_n\right|$ có thể nhỏ hơn một số dương bé tùy ý , kể tử một số hạng nào đó trở đi.

Kí hiệu $\underset{n\to +\mathrm{\infty }}{lim}{u}_n=0$ hay $u_n\to 0$ khi $n\to +\mathrm{\infty }$ hay $lim{u}_n=0$.

- Dãy số $\left(u_n\right)$có giới hạn là số thực a khi n dần tới dương vô cực, nếu $\underset{n\to +\mathrm{\infty }}{lim}\left(u_n-a\right)=0$, kí hiệu $\underset{n\to +\mathrm{\infty }}{lim}{u}_n=a$hay $u_n\to a$ khi $n\to +\mathrm{\infty }$hay $lim{u}_n=a$.

* Chú ý: Nếu $u_n=c$ (c là hằng số) thì $\underset{n\to +\mathrm{\infty }}{lim}{u}_n=c$

2. Một số giới hạn cơ bản

+ $lim\frac{1}{n}=0,lim\frac{1}{n^k}=0,k\in \mathbb{Z}.$

+ $lim\frac{c}{n}=0,lim\frac{c}{n^k}=0,k\in \mathbb{Z}$, c là hằng số.

+ Nếu $\left|q\right|<1$ thì $lim{q}^n=0$

+ $lim{\left(1+\frac{1}{n}\right)}^n=e$

3. Định lí về giới hạn hữu hạn của dãy số

a, Nếu $\underset{n\to +\mathrm{\infty }}{lim}{u}_n=a,\underset{n\to +\mathrm{\infty }}{lim}{v}_n=b$ thì

$\underset{n\to +\mathrm{\infty }}{lim}(u_n\pm v_n)=a\pm b$

$\underset{n\to +\mathrm{\infty }}{lim}(u_n.v_n)=a.b$

$\underset{n\to +\mathrm{\infty }}{lim}(\frac{u_n}{v_n})=\frac{a}{b}\left(b\ne 0\right)$

b, Nếu $u_n\ge 0$ thì với mọi n và $\underset{n\to +\mathrm{\infty }}{lim}{u}_n=a$ thì $a\ge 0$ và $\underset{n\to +\mathrm{\infty }}{lim}\sqrt{u_n}=\sqrt{a}$.

3. Tổng của cấp số nhân lùi vô hạn

Cấp số nhân lùi vô hạn $u_1,u_{1}q,...,u_1{q}^{n-1},...$ có công bội q thỏa mãn $\left|q\right|<1$ được gọi là cấp số nhân lùi vô hạn.

Tổng của cấp số nhân lùi vô hạn là:

$S=\frac{u_1}{1-q}\left(\left|q\right|<1\right)$

4. Giới hạn vô cực

- Dãy số $\left(u_n\right)$ được gọi là có giới hạn $+\mathrm{\infty }$khi $n\to +\mathrm{\infty }$ nếu $u_n$ có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi, kí hiệu $\underset{x\to +\mathrm{\infty }}{lim}{u}_n=+\mathrm{\infty }$ hay $u_n\to +\mathrm{\infty }$ khi $n\to +\mathrm{\infty }$.

- Dãy số $\left(u_n\right)$ được gọi là có giới hạn $-\mathrm{\infty }$khi $n\to +\mathrm{\infty }$ nếu $\underset{x\to +\mathrm{\infty }}{lim}\left(-u_n\right)=+\mathrm{\infty }$, kí hiệu $\underset{x\to +\mathrm{\infty }}{lim}{u}_n=-\mathrm{\infty }$ hay $u_n\to -\mathrm{\infty }$ khi $n\to +\mathrm{\infty }$.

*Nhận xét:

• $\begin{array}{l}lim{n}^k=+\mathrm{\infty },k\in {\mathbb{Z}}^{+}\\ lim{q}^n=+\mathrm{\infty };q\in \mathbb{R},q>1.\end{array}$
• Nếu $\underset{x\to +\mathrm{\infty }}{lim}{u}_n=a$và $\underset{x\to +\mathrm{\infty }}{lim}{v}_n=+\mathrm{\infty }$(hoặc$\underset{x\to +\mathrm{\infty }}{lim}{v}_n=-\mathrm{\infty }$) thì $\underset{n\to +\mathrm{\infty }}{lim}(\frac{u_n}{v_n})=0$.
• Nếu $\underset{x\to +\mathrm{\infty }}{lim}{u}_n=a>0$và $\underset{x\to +\mathrm{\infty }}{lim}{v}_n=0,\mathrm{\forall }n$ thì $\underset{n\to +\mathrm{\infty }}{lim}(\frac{u_n}{v_n})=+\mathrm{\infty }$.
• $\underset{n\to +\mathrm{\infty }}{lim}(\frac{u_n}{v_n})=+\mathrm{\infty }$.
• Nếu $\underset{x\to +\mathrm{\infty }}{lim}{u}_n=+\mathrm{\infty }\iff \underset{n\to +\mathrm{\infty }}{lim}(-u_n)=-\mathrm{\infty }$

Xem thêm lời giải bài tập Toán 11 Cánh diều hay, chi tiết khác:

Bài tập cuối chương 2

Bài 1: Giới hạn của dãy số

Bài 2: Giới hạn của hàm số

Bài 3: Hàm số liên tục

Bài tập cuối chương 3