Toán 11 Bài 1 (Cánh diều): Hai đường thẳng vuông góc
Với giải bài tập Toán lớp 11 Bài 1: Hai đường thẳng vuông góc sách Cánh diều hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 11 Bài 1.
Giải Toán 11 Bài 1: Hai đường thẳng vuông góc
Trong không gian, thế nào là hai đường thẳng vuông góc với nhau?
Lời giải:
Dựa vào hình vẽ ta thấy hai đường thẳng a và b lần lượt nằm trong hai mặt phẳng tường bên và sàn nhà, mà mặt phẳng tường bên và sàn nhà vuông góc với nhau. Vậy nên trong không gian, hai đường thẳng vuông góc với nhau là hai đường thẳng nằm trong hai mặt phẳng vuông góc với nhau.
1. Góc giữa hai đường thẳng trong không gian
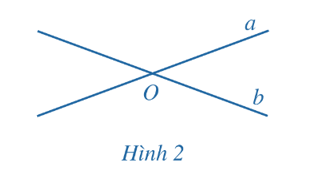
Hoạt động 1 trang 77 Toán 11 Tập 2: Trong mặt phẳng cho hai đường thẳng a, b.
b) Nếu a // b thì góc giữa a và b bằng bao nhiêu độ?
c) Nếu a và b trùng nhau thì góc giữa a và b bằng bao nhiêu độ?
Lời giải:
a) Nếu a và b cắt nhau tại O thì góc giữa hai đường thẳng a, b là góc nhỏ nhất trong 4 góc được tạo thành hay góc giữa hai đường thẳng a, b lớn hơn 0° và không vượt quá 90°.
b) Nếu a // b thì góc giữa hai đường thẳng a và b bằng 0°.
c) Nếu a và b trùng nhau thì góc giữa a và b bằng 0°.
Lời giải:
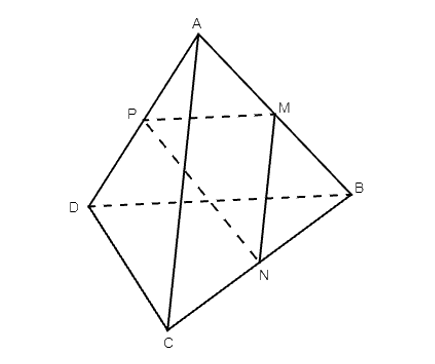
Xét tam giác ABC có: M, N lần lượt là trung điểm của AB và BC.
Suy ra MN là đường trung bình của tam giác ABC.
Nên MN // AC. (1)
Xét tam giác ABD có: M, P lần lượt là trung điểm của AB và AD.
Suy ra MP là đường trung bình của tam giác ABD.
Nên MP // BD. (2)
Từ (1) và (2) ta có: (AC, BD) = (MN, MP) = < = 60° (do tam giác MNP đều).
Vậy góc giữa hai đường thẳng AC và BD bằng 60°.
2. Hai đường thẳng vuông góc trong không gian
Lời giải:
Do hai đường thẳng a và b vuông góc với nhau nên góc giữa a và b bằng 90°.
Lời giải:
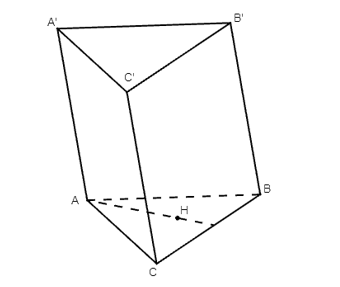
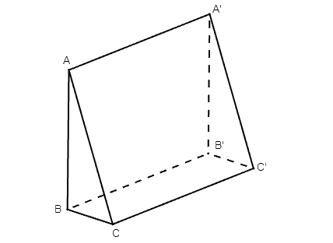
Do H là trực tâm tam giác ABC nên AH ⊥ BC. (1)
Do ABC.A’B’C’ là hình lăng trụ nên B’C’ // BC. (2)
Từ (1), (2) ta có AH ⊥ B’C’.
Bài tập
Lời giải:
Ta có 5 cặp đường thẳng vuông góc là: a và b; a và c; b và c; c và d; a và d.
⦁ 4 cặp đường thẳng vuông góc a và b; a và c; b và c; c và d ta có thể dễ dàng nhìn thấy được từ hình vẽ.
⦁ Cặp đường thẳng a và d vuông góc với nhau: vì a ⊥ b mà b // d suy ra a ⊥ d.
Lời giải:
⦁ Do ABB’A’ là hình chữ nhật nên AB ⊥ BB’.
Do BCC’B’ là hình chữ nhật nên CC’ // BB’.
Từ đó ta có AB ⊥ CC’.
⦁ Do BCC’B’ là hình chữ nhật nên BC ⊥ CC’.
Do AA'C'C là hình chữ nhật nên AA’ // CC’.
Từ đó ta có BC ⊥ AA’ hay AA’ ⊥ BC.
Lời giải:
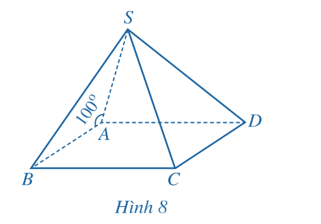
a) Vì nên
Vậy góc giữa hai đường thẳng SA và AB bằng 80°.
b) Do ABCD là hình bình hành nên AB // CD.
Suy ra (SA, CD) = (SA, AB) = 80° (theo câu a).
Vậy góc giữa hai đường thẳng SA và CD bằng 80°.
Lời giải:
Bạn Hoa nói sai. Vì nếu a, b, c cùng nằm trong một mặt phẳng.
Theo quan hệ từ vuông góc tới song song trong mặt phẳng ta có: a ⊥ b và b ⊥ c thì a // b.
Lý thuyết Hai đường thẳng vuông góc
1. Góc giữa hai đường thẳng trong không gian
Góc giữa hai đường thẳng a và b trong không gian là góc giữa hai đường thẳng a’ và b’ cùng đi qua một điểm O và lần lượt song song (hoặc trùng) với a và b, kí hiệu (a, b) hoặc .
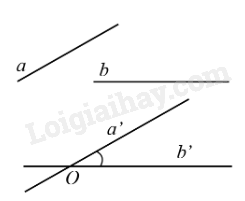
Nhận xét:
- Góc giữa hai đường thẳng a, b không phụ thuộc vào vị trí điểm O. Thông thường, khi tìm góc giữa hai đường thẳng a, b, ta chọn O thuộc a hoặc O thuộc b.
- Góc giữa hai đường thẳng a, b bằng góc giữa hai đường thẳng b, a, tức là (a, b) = (b, a).
- Góc giữa hai đường thẳng không vượt quá .
- Nếu a // b thì (a, c) = (b, c) với mọi đường thẳng c trong không gian.
2. Hai đường thẳng vuông góc trong không gian
Hai đường thẳng được gọi là vuông góc với nhau nếu góc giữa chúng bằng .
Khi hai đường thẳng a và b vuông góc với nhau, ta kí hiệu .
Nhận xét: Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó vuông góc với đường thẳng còn lại.
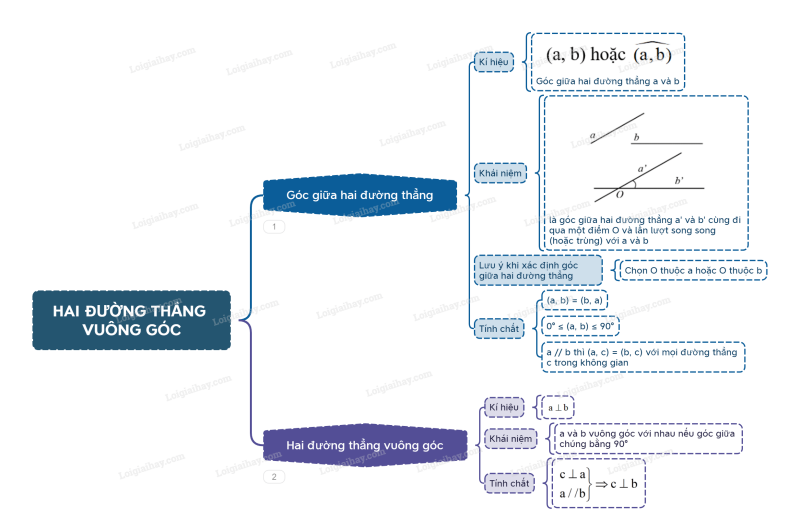
Sơ đồ tư duy Hai đường thẳng vuông góc
Xem thêm Lời giải bài tập Toán 11 Cánh diều hay, chi tiết khác:
Bài tập cuối chương 7 trang 76
Bài 3: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện
Bài 4: Hai mặt phẳng vuông góc
Bài 6: Hình lăng trụ đứng. Hình chóp đều. Thể tích của một số hình khối
Xem thêm các chương trình khác:
- Soạn văn lớp 11 Cánh diều (hay nhất)
- Văn mẫu lớp 11 - Cánh diều
- Tóm tắt tác phẩm Ngữ văn 11 – Cánh diều
- Tác giả tác phẩm Ngữ văn 11 - Cánh diều
- Giải SBT Ngữ văn 11 – Cánh diều
- Bố cục tác phẩm Ngữ văn 11 – Cánh diều
- Giải Chuyên đề học tập Ngữ văn 11 – Cánh diều
- Nội dung chính tác phẩm Ngữ văn lớp 11 – Cánh diều
- Soạn văn 11 Cánh diều (ngắn nhất)
- Giải sgk Tiếng Anh 11 – ilearn Smart World
- Giải sbt Tiếng Anh 11 - ilearn Smart World
- Trọn bộ Từ vựng Tiếng Anh 11 ilearn Smart World đầy đủ nhất
- Giải sgk Vật lí 11 – Cánh diều
- Lý thuyết Vật lí 11 – Cánh diều
- Giải sbt Vật lí 11 – Cánh diều
- Giải Chuyên đề học tập Vật lí 11 – Cánh diều
- Giải sgk Hóa học 11 – Cánh diều
- Giải Chuyên đề học tập Hóa học 11 – Cánh diều
- Lý thuyết Hóa 11 - Cánh diều
- Giải sbt Hóa học 11 – Cánh diều
- Giải sgk Sinh học 11 – Cánh diều
- Lý thuyết Sinh học 11 – Cánh diều
- Giải Chuyên đề học tập Sinh học 11 – Cánh diều
- Giải sbt Sinh học 11 – Cánh diều
- Giải sgk Giáo dục Kinh tế và Pháp luật 11 – Cánh diều
- Giải Chuyên đề học tập Kinh tế pháp luật 11 – Cánh diều
- Lý thuyết Kinh tế pháp luật 11 – Cánh diều
- Giải sbt Kinh tế pháp luật 11 – Cánh diều
- Giải sgk Lịch sử 11 – Cánh diều
- Giải Chuyên đề học tập Lịch sử 11 – Cánh diều
- Lý thuyết Lịch sử 11 - Cánh diều
- Giải sbt Lịch sử 11 – Cánh diều
- Giải sgk Địa lí 11 – Cánh diều
- Giải Chuyên đề học tập Địa lí 11 – Cánh diều
- Lý thuyết Địa lí 11 - Cánh diều
- Giải sbt Địa lí 11 – Cánh diều
- Giải sgk Công nghệ 11 – Cánh diều
- Lý thuyết Công nghệ 11 - Cánh diều
- Giải sbt Công nghệ 11 – Cánh diều
- Giải sgk Tin học 11 – Cánh diều
- Giải Chuyên đề học tập Tin học 11 – Cánh diều
- Lý thuyết Tin học 11 - Cánh diều
- Giải sbt Tin học 11 – Cánh diều
- Giải sgk Giáo dục quốc phòng an ninh 11 – Cánh diều
- Lý thuyết Giáo dục quốc phòng 11 – Cánh diều
- Giải sbt Giáo dục quốc phòng 11 – Cánh diều
- Giải sgk Hoạt động trải nghiệm 11 – Cánh diều