Toán 11 Bài 2 (Cánh diều): Cấp số cộng

Giải Toán 11 Bài 2: Cấp số cộng

Giải Toán 11 trang 49 Tập 1

Câu hỏi khởi động trang 49 Toán 11 Tập 1: Ruộng bậc thang là một hình thức canh tác có nhiều ở khu vực Tây Bắc và Đông Bắc Việt Nam. Hình ảnh ruộng bậc thang thể hiện nét đẹp văn hóa, là công trình nghệ thuật độc đáo của đồng bào vùng cao phía Bắc. Ruộng bậc thang ở một số nơi đã trở thành những địa chỉ tham quan du lịch đầy hấp dẫn của du khách trong nước và quốc tế.

Một ruộng bậc thang có thửa thấp nhất nằm ở độ cao 1 250 m so với mực nước biểu, độ chênh lệch giữa thửa trên và thửa dưới trung bình là 1,2 m.

Hỏi thửa ruộng ở bậc thứ 10 có độ cao là bao nhiêu so với mực nước biển?

Lời giải:

Ta có thửa ruộng thấp nhất có độ cao u₁ = 1 250 m so với mực nước biển.

Thửa ruộng ở bậc thứ hai cao hơn so với mực nước biển là: u₂ = 1 250 + 1,2 (m).

Thửa ruộng ở bậc thứ ba cao hơn so với mực nước biển là: u₃ = 1 250 + 1,2 + 1,2 = 1 250 + 2.1,2 (m).

...

Thửa ruộng ở bậc thứ 10 cao hơn so với mực nước biển là: u₁₀ = 1 250 + 9.1,2 = 1 260,8 (m)

I. Định nghĩa

Hoạt động 1 trang 49 Toán 11 Tập 1: Cho dãy số – 2; 3; 8; 13; 18; 23; 28. Kể từ số hạng thứ hai, nêu mối liên hệ của mỗi số hạng với số hạng đứng ngay trước nó.

Lời giải:

Số hạng thứ hai là số 3, so với số hạng đầu tiên ta thấy 3 lớn hơn – 2 năm đơn vị.

Số hạng thứ ba là số 8, so với số hạng đứng ngay trước nó ta thấy 8 hơn 3 năm đơn vị.

Số hạng thứ tư là số 13, so với số hạng đứng ngay trước nó ta thấy 13 hơn 8 năm đơn vị.

Số hạng thứ năm là số 18, so với số hạng đứng ngay trước nó ta thấy 18 hơn 13 năm đơn vị.

Số hạng thứ sáu là số 23, so với số hạng đứng ngay trước nó ta thấy 23 hơn 18 năm đơn vị.

Số hạng cuối là số 28, so với số hạng đứng ngay trước nó ta thấy 28 hơn 23 năm đơn vị.

Vậy ta thấy kể từ số hạng thứ hai trở đi số hạng sau hơn số hạng trước năm đơn vị.

Luyện tập 1 trang 49 Toán 11 Tập 1: Cho (u_n) là cấp số cộng u₁ = – 7, u₂ = – 2. Viết năm số hạng đầu của cấp số cộng đó.

Lời giải:

Công sai của cấp số cộng đã cho là: d = u₂ – u₁ = – 2 – (– 7) = 5.

Khi đó công thức tổng quát của cấp số cộng là: u_n = u₁ + (n – 1)d = – 7 + (n – 1).5

Giải Toán 11 trang 50 Tập 1

Luyện tập 2 trang 50 Toán 11 Tập 1: Cho dãy số (u_n) với u_n = – 5n + 7 (n ≥ 1). Dãy (u_n) có là cấp số cộng không? Vì sao?

Lời giải:

Ta có: u_n+1 = – 5(n + 1) + 7 = – 5n – 5 + 7 = – 5n + 2

Xét hiệu u_n+1 – u_n = – 5n + 2 – (– 5n + 7) = – 5

Do đó (u_n) là một cấp số cộng.

II. Số hạng tổng quát

Hoạt động 2 trang 50 Toán 11 Tập 1: Cho cấp số cộng (u_n) có số hạng đầu u₁, công sai d.

a) Viết năm số hạng đầu của cấp số cộng theo u₁ và d.

b) Dự đoán công thức tính u_n theo u₁ theo d.

Lời giải:

a) Năm số hạng đầu của cấp số cộng theo u₁ và d là:

u₁; u₂ = u₁ + d; u₃ = u₁ + 2d, u₄ = u₁ + 3d, u₅ = u₁ + 4d.

Luyện tập 3 trang 50 Toán 11 Tập 1: Hãy giải bài toán trong phần mở đầu.

Lời giải:

Độ cao các thửa ruộng so với mực nước biển tạo thành một cấp số cộng với số hạng đầu u₁ = 1 250 m và công sai d = 1,2 (m).

Khi đó công thức tổng quát của cấp số cộng là: u_n = u₁ + (n – 1).d = 1 250 + (n – 1).1,2.

Vậy độ cao của thửa ruộng thứ 10 so với mực nước biển là:

u₁₀ = 1 250 + (10 – 1).1,2 = 1 260,8 m.

III. Tổng n số hạng đầu của một cấp số cộng

Hoạt động 3 trang 50 Toán 11 Tập 1: Cho cấp số cộng (u_n) có số dạng đầu u₁, công sai d.

a) So sánh các tổng sau: u₁ + u_n; u₂ + u_n-1­; u₃ + u_n-2; ...; u_n + u₁.

b) Đặt S_n = u₁ + u₂ + u₃ + ... + u_n. So sánh n(u_n + u₁) với 2S_n.

Lời giải:

a) Ta có: u₁ + u_n = u₁ + u₁ + (n – 1)d = 2u₁ + (n – 1)d;

u₂ + u_n-1­ = u₁ + d + u₁ + (n – 1 – 1)d = 2u₁ + (n – 1)d;

u₃ + u_n-2 = u₁ + 2d + u₁ + (n – 2 – 1)d = 2u₁ + (n – 1)d;

...

u_n + u₁ = u₁ + (n – 1)d + u₁ = 2u₁ + (n – 1)d.

Ta thấy u₁ + u_n = u₂ + u_n-1­ = u₃ + u_n-2 = ... = u_n + u₁.

b) Ta có: 2S_n = 2.(u₁ + u₂ + u₃ + ... + u_n) = (u₁ + u_n) + (u₂ + u_n-1) + ... + (u_n + u₁)

= 2u₁ + (n – 1)d + 2u₁ + (n – 1)d + 2u₁ + (n – 1)d + ... + 2u₁ + (n – 1)d

= 2n.u₁ + n(n – 1)d

= n(u₁ + u₁ + (n – 1)d)

= n(u₁ + u_n).

Giải Toán 11 trang 51 Tập 1

Luyện tập 4 trang 51 Toán 11 Tập 1: Tính tổng n số hạng đầu của mỗi cấp số cộng sau:

a) 3; 1; – 1; ... với n = 10;

b) 1,2; 1,7; 2,2; ... với n = 15.

Lời giải:

a) Ta có: 3; 1; – 1; ... là cấp số cộng với số hạng đầu u₁ = 3 và công sai d = 1 – 3 = – 2.

Khi đó u₁₀ = 3 + (10 – 1).(– 2) = 3 + (– 18) = – 15.

Tổng của 10 số hạng đầu của cấp số cộng là:

S₁₀ = $\frac{10\left(3+\left(-15\right)\right)}{2}=-60$ .

b) 1,2; 1,7; 2,2; ... với n = 15.

Ta có: 1,2; 1,7; 2,2; ... là cấp số cộng với số hạng ban đầu u₁ = 1,2 và công sai d = 1,7 – 1,2 = 0,5.

Khi đó u₁₅ = 1,2 + (15 – 1).0,5 = 8,2.

Tổng của 15 số hạng đầu của cấp số cộng là:

S₁₅ = $\frac{15\left(1,2+8,2\right)}{2}=70,5$ .

Bài tập

Bài 1 trang 51 Toán 11 Tập 1: Trong các dãy số sau, dãy số nào là cấp cố cộng?

a) 10; – 2; – 14; – 26; – 38;

b) $\frac{1}{2};\frac{5}{4};2;\frac{11}{4};\frac{7}{2}$ ;

c) 1²; 2²; 3²; 4²; 5²;

d) 1; 4; 7; 10; 13.

Lời giải:

a) Ta có: 10; – 2; – 14; – 26; – 38 là cấp số cộng có số hạng đầu u₁ = 10 và công sai của cấp số cộng là: d = – 12.

b) Ta có: $\frac{1}{2};\frac{5}{4};2;\frac{11}{4};\frac{7}{2}$ là cấp số cộng có số hạng đầu là u₁ = $\frac{1}{2}$ và công sai d = $\frac{3}{4}$ .

c) Ta có: 1²; 2²; 3²; 4²; 5² không là cấp số cộng vì 2² – 1² ≠ 3² – 2².

d) Ta có: 1; 4; 7; 10; 13 là cấp số cộng có số hạng đầu là u₁ = 1 và công sai d = 3.

Giải Toán 11 trang 52 Tập 1

Bài 2 trang 52 Toán 11 Tập 1: Trong các dãy số (u_n) với số hạng tổng quát sau, dãy số nào là cấp số cộng? Nếu là cấp số cộng, hãy tìm số hạng đầu u₁ và công sai d.

a) u_n = 3 – 2n;

b) u_n = $\frac{3n+7}{5}$ ;

c) u_n = 3ⁿ.

Lời giải:

a) Ta có: u_n+1 = 3 – 2(n + 1) = 3 – 2n – 2 = 1 – 2n

Suy ra u_n+1 – u_n = 1 – 2n – 3 + 3n = – 2.

Vì vậy đây là một cấp số cộng có số hạng đầu u₁ = 1 và công sai d = – 2.

b) Ta có: u_n+1 = $\frac{3\left(n+1\right)+7}{5}=\frac{3n+10}{5}$

Xét hiệu u_n+1 – u_n = $\frac{3n+10}{5}-\frac{3n+7}{5}=\frac{3}{5}$

Vì vậy đây là một cấp số cộng có số hạng đầu u₁=2 và công sai d=$\frac{3}{5}$ .

c) Ta có: u_n+1 = 3ⁿ⁺¹ = 3.3ⁿ

Xét hiệu u_n+1 – u_n = 3.3ⁿ – 3ⁿ = 2.3ⁿ với n ∈ ℕ*

Vì vậy đây không là một cấp số cộng.

Bài 3 trang 52 Toán 11 Tập 1: Cho cấp số cộng (u_n) có số hạng đầu u₁ = – 3, công sai d = 5.

a) Viết công thức của số hạng tổng quát u_n.

b) Số 492 là số hạng thứ mấy của cấp số cộng trên?

c) Số 300 có là số hạng nào của cấp số cộng trên không?

Lời giải:

a) Ta có công thức số hạng tổng quát của cấp số cộng (u_n) là: u₁ = – 3 + (n – 1).5 = 5n – 8.

b) Xét u_n = 492

⇔ 5n – 8 = 492

⇔ n = 100.

Vậy số 492 là số hạng thứ 100 của cấp số cộng trên.

c) Xét u_n = 300

⇔ 5n – 8 = 300

⇔ n = 61,6 ∉ ℕ*

Vậy không tồn tại số hạng trong cấp số cộng bằng 300.

Bài 4 trang 52 Toán 11 Tập 1: Cho cấp số cộng (u_n) có u₁ = 4, u₂ = 1. Tính u₁₀.

Lời giải:

Công sai của cấp số cộng (u_n) là d = u₂ – u₁ = 1 – 4 = – 3.

Khi đó số hạng tổng quát của cấp số cộng là: u_n = u₁ + (n – 1).d = 4 + (n – 1).(– 3)

Suy ra u₁₀ = 4 + (10 – 1).(– 3) = 31.

Bài 5 trang 52 Toán 11 Tập 1: Cho cấp số cộng (u_n) có u₁ = $\frac{1}{3}$ và u₁ + u₂ + u₃ = – 1.

a) Tìm công sai d và viết công thức của số hạng tổng quát u­_n.

b) Số – 67 là số hạng thứ mấy của cấp số cộng trên.

c) Số 7 có phải là một số hạng của cấp số cộng trên không?

Lời giải:

a) Ta có: u₁ + u₂ + u₃ = – 1

⇒ u₁ + u₁ + d + u₁ + 2d = – 1

⇒ 3u₁ + 3d = – 1

Mà u₁ = $\frac{1}{3}$ nên d = -$\frac{2}{3}$

Khi đó công thức tổng quát của cấp số cộng là: u_n = $\frac{1}{3}-\frac{2}{3}\left(n-1\right)=-\frac{2}{3}n+\frac{1}{3}$ với mọi n ∈ ℕ*.

b) Xét u_n = $-\frac{2}{3}n+\frac{1}{3}$= -67

$\iff -\frac{2}{3}n=\frac{-202}{3}$

$\iff$ n = 101

Vậy số – 67 là số hạng thứ 101 của dãy.

c) Xét u_n = 7

$\iff -\frac{2}{3}n+\frac{1}{3}=7$

$\iff -\frac{2}{3}n=\frac{20}{3}$

⇔ n = – 10 ∉ ℕ*

Vậy số 7 không phải là một số hạng trong cấp số cộng.

Bài 6 trang 52 Toán 11 Tập 1: Tính tổng 100 số hạng đầu của dãy số (u_n) với u_n = 0,3n + 5 với mọi n ≥ 1.

Lời giải:

Ta có: u_n+1 = 0,3.(n + 1) + 5 = 0,3n + 5,3

Xét hiệu u_n+1 – u_n = 0,3n + 5,3 – 0,3n – 5 = 0,3.

Do đó (u_n) là một cấp số cộng với số hạng đầu u₁ = 5,3 và công sai d = 0,3.

Khi đó số hạng tổng quát của cấp số cộng u_n là: u_n = 5,3 + (n – 1).0,3

Suy ra u₁₀₀ = 5,3 + (100 – 1).0,3 = 35.

Vậy tổng của 100 số hạng đầu của dãy số là: S₁₀₀=$\frac{100\left(5,3+35\right)}{2}$= 2 015.

Bài 7 trang 52 Toán 11 Tập 1: Chiều cao (đơn vị: centimet) của một đứa trẻ n tuổi phát triển bình thường được cho bởi công thức:

x_n = 75 + 5(n – 1).

(Nguồn: https://bibabo.vn)

a) Một đứa trẻ phát triển bình thường có chiều cao 3 năm tuổi là bao nhiêu centimet?

b) Dãy số (x_n) có là một cấp số cộng không? Trung bình một năm, chiều cao mỗi đứa trẻ phát triển bình thường tăng lên bao nhiêu centimet?

Lời giải:

a) Chiều cao 3 năm tuổi của một đứa bé phát triển bình thường là:

x₃ = 75 + 5(3 – 1) = 85 (cm).

b) Ta có: x_n+1 = 75 + 5(n + 1 – 1) = 75 + 5n

Xét hiệu x_n+1 – x_n = 75 + 5n – [75 + 5(n – 1)] = 5

Do đó (x_n) là một cấp số cộng có số hạng đầu x₁ = 75 và công sai d = 5

Bài 8 trang 52 Toán 11 Tập 1: Khi kí kết hợp đồng lao động đối với người lao động, một doanh nghiệp đề xuất hai phương án trả lương như sau:

Phương án 1: Năm thứ nhất, tiền lương là 120 triệu. Kể từ năm thứ hai trở đi, mỗi năm, tiền lương được tăng 18 triệu.

Phương án 2: Quý thứ nhất, tiền lương là 24 triệu. Kể từ quý thứ hai trở đi, mỗi quý tiền lương được tăng 1,8 triệu.

Nếu là người được tuyển dụng vào doanh nghiệp trên, em sẽ chọn phương án nào khi:

a) Kí hợp đồng lao động 3 năm?

b) Kí hợp đồng lao động 10 năm?

Lời giải:

+) Theo phương án 1: Gọi (u_n) là dãy số tiền lương của người lao động theo phương án 1 qua mỗi năm. Dãy số (u_n) lập thành một cấp số cộng có số hạng đầu u₁ = 120 và công sai d = 18.

Khi đó số hạng tổng quát của cấp số nhân là: u_n = 120 + (n – 1).18.

+) Theo phương án 2: Gọi (v_n) là dãy số tiền lương của người lao động theo phương án 2 qua từng quý. Dãy số (v_n) lập thành một cấp số cộng có số hạng đầu v₁ = 24 và công sai d = 1,8.

Khi đó số hạng tổng quát của cấp số nhân là v_n = 24 + (n – 1).1,8.

a) Khi kí hợp đồng 3 năm tương đương với 12 quý ta có:

+) Theo phương án 1: u₃ = 120 + (3 – 1).18 = 156 (triệu đồng)

Tổng số tiền lương nhận được sau 3 năm là:

$S_3=\frac{3.\left(120+156\right)}{2}$= 414 (triệu đồng).

+) Theo phương án 2: u₁₂ = 24 + (12 – 1).1,8 = 43,8.

Tổng số tiền lương nhận được sau 3 năm tương ứng với 12 quý là:

$S_{12}=\frac{12.\left(24+43,8\right)}{2}$= 406,8 (triệu đồng).

Vậy nếu được tuyển dụng vào doanh nghiệp và kí hợp đồng lao động 3 năm thì nên theo phương án 1.

b) Khi kí hợp đồng 10 năm tương đương với 40 quý ta có:

+) Theo phương án 1: u₁₀ = 120 + (10 – 1).18 = 282 (triệu đồng)

Tổng số tiền lương nhận được sau 10 năm là:

$S_{10}=\frac{10.\left(120+282\right)}{2}$= 2010 (triệu đồng).

+) Theo phương án 2: u₄₀ = 24 + (40 – 1).1,8 = 94,2.

Tổng số tiền lương nhận được sau 10 năm tương ứng với 40 quý là:

$S_{12}=\frac{40.\left(24+94,2\right)}{2}$= 2 364 (triệu đồng).

Vậy nếu được tuyển dụng vào doanh nghiệp và kí hợp đồng lao động 10 năm thì nên theo phương án 2.

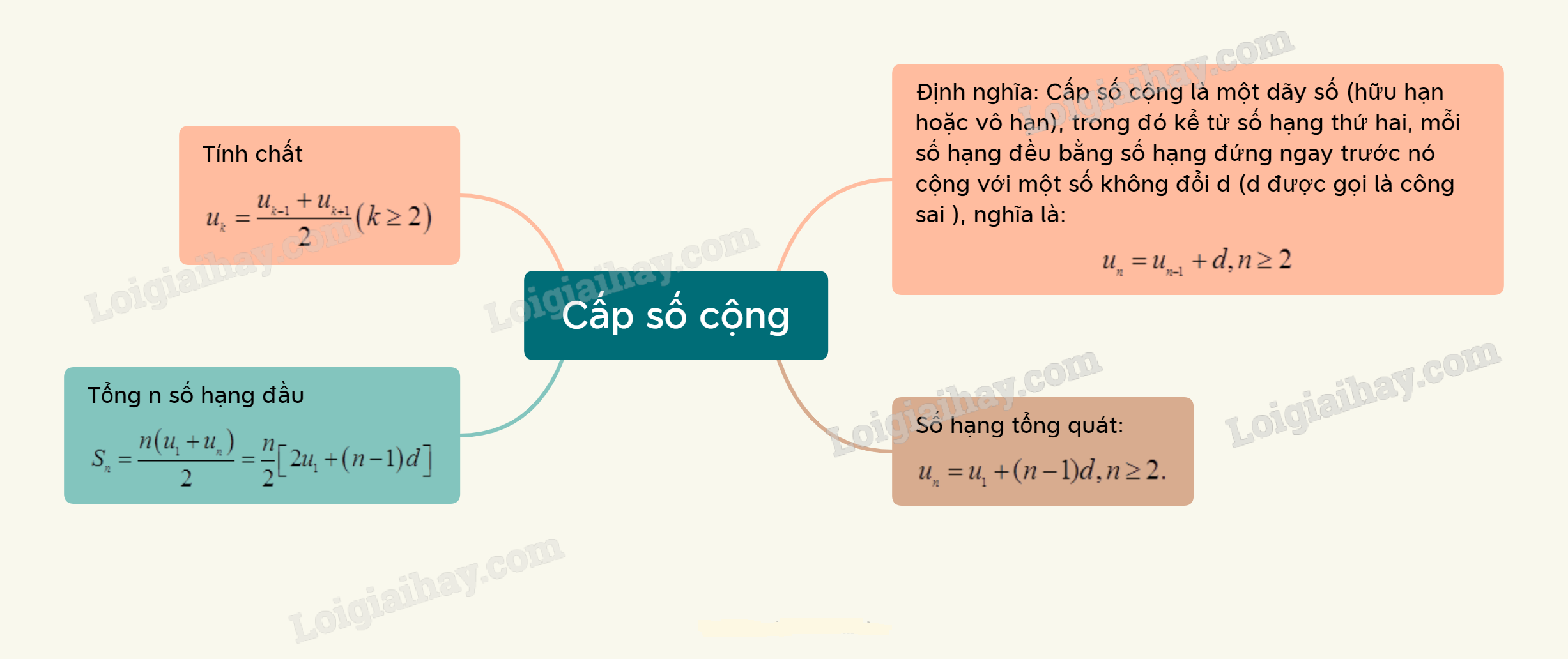
Lý thuyết Cấp số cộng

1. Định nghĩa

Cấp số cộng là một dãy số ,trong đó kể từ số hạng thứ hai, mỗi số hạng đều bằng số hạng đứng ngay trước nó cộng với một số không đổi d. Tức là:

$u_n=u_{n-1}+d,n\ge 2$

Số d được gọi là công sai của cấp số cộng.

* Nhận xét: Nếu $\left(u_n\right)$ là cấp số cộng thì kể từ số hạng thứ 2, mỗi số hạng (trừ số hạng cuối đối với cấp số cộng hữu hạn) đều là trung bình cộng của 2 sô hạng đứng kề nó trong dãy, tức là:

$u_k=\frac{u_{k-1}+u_{k+1}}{2}\left(k\ge 2\right)$

2. Số hạng tổng quát

Nếu cấp số cộng $\left(u_n\right)$ có số hạng đầu là $u_1$ và công sai d thì số hạng tổng quát $u_n$của nó được xác định theo công thức$u_n=u_1+(n-1)d,n\ge 2.$

3. Tổng n số hạng đầu của một cấp số cộng

Cho cấp số cộng $\left(u_n\right)$với công sai d. Đặt $S_n=u_1+u_2+u_3+...+u_n$. Khi đó

$S_n=\frac{n\left(u_1+u_n\right)}{2}=\frac{n}{2}\left[2u_1+\left(n-1\right)d\right]$

Xem thêm lời giải bài tập Toán 11 Cánh diều hay, chi tiết khác:

Bài 1: Dãy số

Bài 3: Cấp số nhân

Bài tập cuối chương 2

Bài 1: Giới hạn của dãy số

Bài 2: Giới hạn của hàm số