Giải Toán 10 trang 38 Tập 1 Chân trời sáng tạo

Giải Toán 10 trang 38 Tập 1

Bài 2 trang 38 Toán lớp 10 Tập 1: Một nhà máy sản xuất hai loại thuốc trừ sâu nông nghiệp là A và B. Cứ sản xuất mỗi thùng loại A thì nhà máy thải ra 0,25 kg khí cacbon dioxide (CO₂) và 0,60 kg khí sulffur dioxide (SO₂), sản xuất mỗi thùng loại B thì thải ra 0,50 kg CO₂  và  0,20 kg SO₂. Biết rằng, quy định hạn chế sản lượng (CO₂) của nhà máy tối đa là 75 kg và SO₂ tối đa là 90 kg mỗi ngày.

a) Tìm hệ bất phương trình mô tả số thùng của mỗi loại thuốc trừ sâu mà nhà máy có thể sản xuất mỗi ngày để đáp ứng các điều kiện hạn chế trên. Biểu diễn miền nghiệm của hệ bất phương trình đó trên mặt phẳng tọa độ.

b) Việc nhà máy sản xuất 100 thùng loại A và 80 thùng loại B mỗi ngày có phù hợp với quy định không ?

c) Việc nhà máy sản xuất 60 thùng loại A và 160 thùng loại B mỗi ngày có phù hợp với quy định không ?

Lời giải:

a) Gọi x và y lần lượt là số lượng thùng thuốc trừ sâu loại A và B.

Theo đề ta có:

+ Quy định hạn chế sản lượng CO₂ của nhà máy tối đa là 75 kg mỗi ngày nên 0,25x + 0,5y ≤ 75 hay x + 2y ≤ 300

+ Quy định hạn chế sản lượng SO₂ của nhà máy tối đa là 90 kg mỗi ngày nên 0,6x + 0,2y ≤ 90 hay 3x + y ≤ 450

Do đó, ta có hệ bất phương trình sau:$\left\{\begin{array}{l}x+2y\le 300\\ 3x+y\le 450\\ x\ge 0\\ y\ge 0\end{array}\right.$

Biểu diễn miền nghiệm của hệ bất phương trình này trên hệ trục toạ độ Oxy:

+ Xác định miền nghiệm của bất phương trình : x + 2y -300 ≤ 0

Vẽ đường thẳng d: x + 2y - 300 = 0 đi qua hai điểm (300; 0); (0; 150).

Xét gốc toạ độ O(0; 0) ta thấy: O ∉ d và 0 + 2.0 - 300 = -300 < 0. Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng chứa điểm O

+ Xác định miền nghiệm của bất phương trình : 3x + y - 450 ≤ 0

Vẽ đường thẳng a: 3x + y - 450 = 0 đi qua hai điểm (150; 0); (0; 450).

Xét gốc toạ độ O(0; 0) ta thấy: O ∉ a và 3.0 + 0 - 450 = -450 < 0. Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng chứa điểm O

+ Miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng phía trên trục hoành

+ Miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng phía bên phải trục tung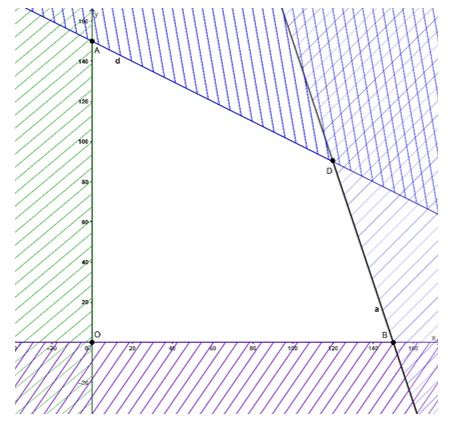

Miền nghiệm là miền tứ giác OADB với các đỉnh O(0; 0); A(0; 150); B(150; 0) và D(120;90).

b) Với x = 100 và y = 80 ta có:

+) 0,25.100 + 0,5.80 – 75 = – 10 < 0;

+) 0,6.100  + 0,2.80 – 90 = –14 < 0;

Vậy việc nhà máy sản xuất 100 thùng loại A và 80 thùng loại B mỗi ngày là hợp lí.

c) Với x  = 60 và y = 160 ta có:

+) 0,25.60 + 0,5.160 – 75 = 20 > 0;

+) 0,6.60  + 0,2.160 – 90 = –22 < 0;

Vậy việc nhà máy sản xuất 60 thùng loại A và 160 thùng loại B mỗi ngày là không phù hợp quy định.

Bài 3 trang 38 Toán lớp 10 Tập 1: Bạn Lan thu xếp được không quá 10 giờ để làm hai loại đèn trung thu tặng cho các trẻ em khuyết tật. Loại đèn hình con cá cần 2 giờ để làm xong 1 cái, còn loại đèn ông sao chỉ cần 1 giờ để làm xong 1 cái. Gọi x, y lần lượt là số đèn hình con cá và đèn ông sao bạn Lan sẽ làm. Hãy lập hệ bất phương trình mô tả điều kiện của x, y và biểu diễn miền nghiệm của hệ bất phương trình đó.

Lời giải:

Gọi x, y là số đèn hình con cá và đèn ông sao bạn Lan sẽ làm.

Theo đề ta có:

+ Tổng thời gian để làm xong x cái đèn hình con cá và y cái đèn hình ngôi sao là: 2x + y (giờ).

+ Thời gian bạn Lan có thể thực hiện không quá 10 giờ nên 2x + y ≤ 10 hay 2x + y -10 ≤ 0.

Từ đó, ta có hệ bất phương trình sau: $\left\{\begin{array}{l}2x+y\le 10\\ x\ge 0\\ y\ge 0\end{array}\right.$

Biểu diễn từng miền nghiệm của mỗi bất phương trình trên mặt phẳng Oxy:

+ Xác định miền nghiệm của bất phương trình 2x + y -10 ≤ 0

Vẽ đường thẳng d: 2x + y - 10 = 0 đi qua hai điểm (5; 0); (0; 10).

Xét gốc toạ độ O(0; 0) ta thấy: O ∉ d và 2.0 + 0 - 10 = - 10 < 0. Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng chứa điểm O

+ Miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng phía trên trục hoành

+ Miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng phía bên phải trục tung

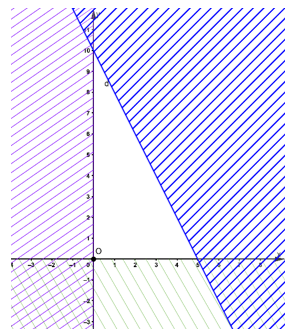
Miền màu trắng (không bị gạch chéo) là phần biểu diễn miền nghiệm của bất phương trình đã cho.

Bài 4 trang 38 Toán lớp 10 Tập 1: Một học sinh dự định vẽ các tấm thiệp xuân bằng tay để bàn trong một hội chợ Tết. Cần 2 giờ để vẽ một tấm thiệp loại nhỏ có giá 10 nghìn đồng và 3 giờ để vẽ một tấm thiệp lớn có giá 20 nghìn đồng. Học sinh này chỉ có 30 giờ để vẽ và ban tổ chức hội chợ yêu cầu phải vẽ ít nhất 12 tấm. Hãy cho biết bạn ấy cần vẽ bao nhiêu tấm thiệp mỗi loại để có được nhiều tiền nhất.

Lời giải:

Gọi x và y lần lượt là số thiệp nhỏ và thiệp lớn bạn học sinh cần chuẩn bị.

Theo đề ta có:

+ Tổng thời gian để vẽ  x chiếc thiệp nhỏ và y chiếc thiệp lớn là : 2x+3y (giờ)

+ Học sinh chỉ có 30 giờ để vẽ nên 2x + 3y ≤ 30 hay 2x + 3y -30 ≤ 0

+ Hội chợ yêu cầu cần ít nhất 12 tấm thiệp nên x + y ≥ 12 hay x + y – 12 ≥ 0 

Theo đề ta có hệ bất phương trình sau :$\left\{\begin{array}{l}2x+3y\le 30\\ x+y\ge 12\\ x\ge 0\\ y\ge 0\end{array}\right.$

Biểu diễn từng miền nghiệm của mỗi bất phương trình trên mặt phẳng Oxy:

+ Xác định miền nghiệm của bất phương trình 2x + 3y -30 ≤ 0

Vẽ đường thẳng d: 2x + 3y - 30 = 0  đi qua hai điểm (15; 0); (0; 10).

Xét gốc toạ độ O(0; 0) ta thấy: O ∉ d và 2.0 + 3.0 - 30 = - 30 < 0. Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng chứa điểm O

+ Xác định miền nghiệm của bất phương trình x + y – 12 ≥ 0 

Vẽ đường thẳng a: x + y - 12 = 0  đi qua hai điểm (12; 0); (0; 12).

Xét gốc toạ độ O(0; 0) ta thấy: O ∉ a và 0 + 0 - 12 = - 12 < 0. Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không chứa điểm O

+ Miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng phía trên trục hoành

+ Miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng phía bên phải trục tung

Khi đó ta có hình vẽ như sau:

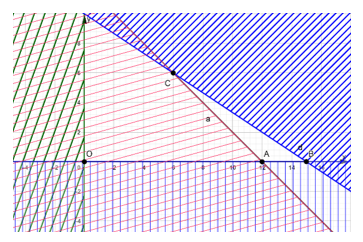Miền nghiệm là phần màu trắng với các đỉnh A(12; 0); B(15; 0); C(6; 6).

Gọi F là số tiền (đơn vị: nghìn đồng) thu được khi bán thiệp, ta có: F = 10x + 20y.

Giá trị của F tại các đỉnh của miền nghiệm là:

Tại A(12; 0): F = 10.12 + 20.0 = 120;

Tại B(15; 0): F = 10.15 + 20.0 = 150;

Tại C(6; 6): F = 10.6 + 20.6 = 180;

F đạt giá trị lớn nhất bằng 180 tại C(6; 6).

Vậy cần phải vẽ 6 tấm thiệp loại nhỏ và 6 tấm thiệp loại lớn để đạt được doanh thu cao nhất.

Bài 5 trang 38 Toán lớp 10 Tập 1: Trong một tuần, bạn Mạnh có thể thu xếp được tối đa 12 giờ để tập thể dục giảm cân bằng hai môn : đạp xe và tập cử tạ tại phòng tập. Cho biết mỗi giờ đạp xe sẽ tiêu hao 350 calo và không tốn chi phí, mỗi giờ tập cử tạ sẽ tiêu hao 700 calo với chi phí 50 000 đồng/giờ. Mạnh muốn tiêu hao nhiều calo nhưng không được vượt quá 7 000 calo một tuần. Hãy giúp bạn Mạnh tính số giờ đạp xe và số giờ tập tạ một tuần trong hai trường hợp sau :

a) Mạnh muốn chi phí tập luyện là ít nhất.

b) Mạnh muốn số calo tiêu hao là lớn nhất.

Lời giải:

Gọi x và y lần lượt là số giờ đạp xe và số giờ tập tạ của bạn Mạnh trong một tuần (x ≥ 0, y ≥ 0)

Theo đề ta có:

+ Thời gian tập thể dục tối đã của Mạnh trong tuần tối đa là 12 giờ nên x + y ≤ 12

+ Lượng tiêu thụ calo không vượt quá 7000 calo một tuần nên 350x + 700y ≤ 7000 hay x + 2y ≤ 20

Theo đề ta có hệ bất phương trình sau:$\left\{\begin{array}{l}x+y\le 12\\ x+2y\le 20\\ x\ge 0\\ y\ge 0\end{array}\right.$ 

Biểu diễn từng miền nghiệm của mỗi bất phương trình trên mặt phẳng Oxy:

+ Xác định miền nghiệm của bất phương trình x + y ≤ 12 hay x + y – 12 ≤ 0

Vẽ đường thẳng d: x + y – 12 = 0 đi qua hai điểm (12; 0) và (0; 12).

Xét gốc toạ độ O(0; 0) ta thấy: O ∉ d và 0 + 0 – 12 = - 12 < 0. Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng chứa điểm O

+ Xác định miền nghiệm của bất phương trình x + 2y ≤ 20 hay x + 2y – 20 ≤  0

Vẽ đường thẳng a: x + 2y - 20 = 0  đi qua hai điểm (20; 0) và (0; 10).

Xét gốc toạ độ O(0; 0) ta thấy: O ∉ a và 0 + 2.0 – 20 = - 20 < 0. Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng chứa điểm O

+ Miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng phía bên phải trục tung.

+ Miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng phía trên trục hoành.

Khi đó ta có hình vẽ như sau:

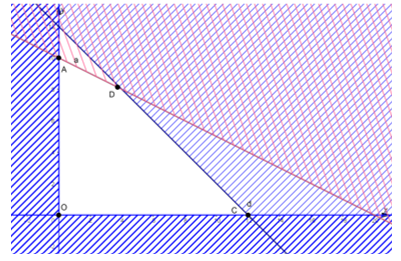
Miền nghiệm là miền tứ giác OADC với đỉnh O(0; 0); A(0; 10); D(4; 8); C(12; 0).

a) Gọi F là chi phí tập luyện của Mạnh trong 1 tuần (đơn vị: nghìn đồng), ta có:

F = 50y.

Các giá trị của biểu thức F tại các đỉnh của đa giác là:

Tại O(0; 0): F= 50.0 = 0;

Tại A(0; 10): F = 50.10 = 500;

Tại D(4; 8): F = 50.8 = 400;

Tại C(12;0): F = 50.0 = 0.

F đạt giá trị nhỏ nhất F = 0 tại O(0; 0) và C(12;0)

Vậy để tiết kiệm chi phí tập luyện thì bạn Mạnh đạp xe 12 giờ, không tập tạ hoặc không tham gia tập thể dục.

b) Gọi H là số calo bạn Mạnh muốn tiêu thụ: H = 350x + 700y.

Các giá trị của biểu thức H tại các đỉnh của đa giác là:

Tại O(0; 0): H= 350.0 + 700.0 = 0;

Tại A(0; 10): H = 350.0 + 700.10 = 7 000;

Tại D(4; 8): H = 350.4 + 700.8 = 7 000;

Tại C(12;0): H = 350.12 + 700.0 = 4 200;

H đạt giá trị lớn nhất H = 7000 tại A(0; 10) và D(4; 8).

Vậy để tiêu thụ lượng calo nhiều nhất Mạnh có thể tập tạ 10 giờ hoặc có thể đạp xe 4 giờ và tập tạ 8 giờ

Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Giải Toán 10 trang 33 Tập 1

Giải Toán 10 trang 34 Tập 1

Giải Toán 10 trang 35 Tập 1

Giải Toán 10 trang 37 Tập 1

Giải Toán 10 trang 38 Tập 1

Xem thêm lời giải bài tập Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương 2

Bài 1: Hàm số và đồ thị

Bài 2: Hàm số bậc hai

Bài tập cuối chương 3

Bài 1: Giá trị lượng giác của một góc từ 0 độ đến 180 độ