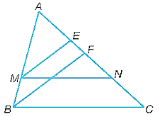
Cho tam giác ABC và hai điểm M, N lần lượt nằm trên hai cạnh AB, AC sao cho MN song song với BC

Lời giải Bài 9.23 trang 56 SBT Toán 8 Tập 2 sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong sách bài tập Toán 8.

1 661 05/12/2023

Trang trước

Trang sau

Giải SBT Toán 8 (Kết nối tri thức) Bài 34: Ba trường hợp đồng dạng của hai tam giác

Bài 9.23 trang 56 SBT Toán lớp 8 Tập 2: Cho tam giác ABC và hai điểm M, N lần lượt nằm trên hai cạnh AB, AC sao cho MN song song với BC. Gọi ME, BF lần lượt là phân giác của các góc M, B của các tam giác AMN và tam giác ABC. Chứng minh rằng:

a) ∆MEN ᔕ ∆BFC.

b) $\frac{A E}{A F} = \frac{M N}{B C}$ .

Lời giải:

Cho tam giác ABC và hai điểm M, N lần lượt nằm trên hai cạnh AB, AC sao cho MN song song

a)

Vì MN song song với BC (gt) nên

$\hat{E N M} = \hat{C}$ (hai góc đồng vị);

$\hat{A M N} = \hat{A B C}$ (hai góc đồng vị).

Mà ME, BF lần lượt là phân giác của các góc M, B của các tam giác AMN và tam giác ABC nên $\hat{E M N} = \frac{1}{2} \hat{A M N}$ và $\hat{F B C} = \frac{1}{2} \hat{A B C}$ . Do đó, $\hat{E M N} = \hat{F B C}$ .

Tam giác MEN và tam giác BFC có:

$\hat{E N M} = \hat{C}$ (cmt)

$\hat{E M N} = \hat{F B C}$ (cmt)

Do đó, tam giác MEN đồng dạng với tam giác BFC (g.g).

b)

Tam giác ABC có:

MN song song với BC

Nên theo hệ quả định lý Thalès ta có:

$\frac{M N}{B C} = \frac{A M}{A B}$ (1).

Vì ME, BF lần lượt là phân giác của $\hat{M}$ , $\hat{B}$ của tam giác AMN và tam giác ABC nên $\hat{E M A} = \frac{1}{2} \hat{A M N} = \frac{1}{2} \hat{A B C} = \hat{F B A}$ .

Do đó $\hat{E M A} = \hat{F B A}$ , mà hai góc này ở vị trí đồng vị nên ME song song với BF.

Tam giác ABF có ME song song với BF nên theo hệ quả định lý Thalès ta có:

$\frac{A E}{A F} = \frac{A M}{A B}$ (2).

Từ (1) và (2) ta có: $\frac{A E}{A F} = \frac{M N}{B C}$ .

Xem thêm Lời giải bài tập SBT Toán 8 Kết nối tri thức hay, chi tiết khác:

Bài 9.12 trang 55 SBT Toán lớp 8 Tập 2: Hai tam giác có độ dài ba cạnh như sau có đồng dạng không ? Vì sao ?...

Bài 9.13 trang 55 SBT Toán lớp 8 Tập 2: Cho hai tam giác ABC và DEF lần lượt có chu vi là 15 cm và 20 cm...

Bài 9.14 trang 55 SBT Toán lớp 8 Tập 2: Cho hai tam giác ABC và MNP thỏa mãn 2AB = 3AC = 4BC...

Bài 9.15 trang 55 SBT Toán lớp 8 Tập 2: Cho tam giác ABC và điểm O nằm trong tam giác....

Bài 9.16 trang 55 SBT Toán lớp 8 Tập 2: Cho tam giác ABC và các điểm M, N, P...

Bài 9.17 trang 55 SBT Toán lớp 8 Tập 2: Cho tứ giác ABCD với AB = 2 cm, AD = 3 cm, BD = 4 cm,...

Bài 9.18 trang 55 SBT Toán lớp 8 Tập 2: Cho tam giác ABC có độ dài các cạnh là AB = 4 cm, BC = 5 cm, CA = 6 cm....

Bài 9.19 trang 55 SBT Toán lớp 8 Tập 2: Với hai tam giác ABC và DEF...

Bài 9.20 trang 56 SBT Toán lớp 8 Tập 2: Với hai tam giác bất kì ABC và MNP

Bài 9.21 trang 56 SBT Toán lớp 8 Tập 2: Cho hai điểm M, N lần lượt nằm trên hai cạnh AB, AC...

Bài 9.22 trang 56 SBT Toán lớp 8 Tập 2: Cho tam giác ABC và hai điểm P, Q lần lượt nằm...

Bài 9.23 trang 56 SBT Toán lớp 8 Tập 2: Cho tam giác ABC và hai điểm M, N lần lượt nằm trên hai cạnh AB, AC...

Bài 9.24 trang 56 SBT Toán lớp 8 Tập 2: Cho hình thang ABCD (AB // CD). Biết rằng AB = 2 cm...

Bài 9.25 trang 56 SBT Toán lớp 8 Tập 2: Cho hình thang ABCD (AB // CD). Biết rằng AD cắt BC tại E, AC cắt BD tại F....

Bài 9.26 trang 56 SBT Toán lớp 8 Tập 2: Cho tam giác ABC với AB = 6 cm, AC = 9 cm...

Bài 9.27 trang 57 SBT Toán lớp 8 Tập 2: Cho tứ giác ABCD như Hình 9.6. Biết rằng AB = 2 cm, AC = 4 cm, AD = 8 cm...

Bài 9.28 trang 57 SBT Toán lớp 8 Tập 2: Cho tam giác ABC và điểm D trên cạnh AC...

Bài 9.29 trang 57 SBT Toán lớp 8 Tập 2: Cho hai điểm M, N lần lượt nằm trên các cạnh AB, AC...

Bài 9.30 trang 57 SBT Toán lớp 8 Tập 2: Cho tam giác ABC với AB = 6 cm, AC = 4 cm, BC = 5 cm....

Xem thêm Lời giải bài tập SBT Toán 8 Kết nối tri thức hay, chi tiết khác:

Bài 33: Hai tam giác đồng dạng

Bài 35: Định lí Pythagore và ứng dụng

Bài 36: Các trường hợp đồng dạng của hai tam giác vuông

Bài 37: Hình đồng dạng

Bài tập cuối chương 9

1 661 05/12/2023

Trang trước

Trang sau

Xem thêm các chương trình khác: