Toán 9 Bài 11 (Kết nối tri thức): Tỉ số lượng giác của góc nhọn
Với giải bài tập Toán lớp 9 Bài 11: Tỉ số lượng giác của góc nhọn sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 9 Bài 11.
Giải Toán 9 Bài 11: Tỉ số lượng giác của góc nhọn
Lời giải:
Sau bài học này, chúng ta sẽ giải quyết được câu hỏi trên như sau:
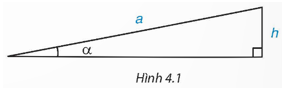
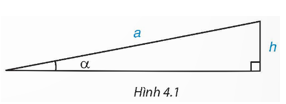
Theo định nghĩa tỉ số lượng giác sin, ta có sinα=ha.
Vậy ta sẽ xác định được “góc dốc” α của một đoạn đường dốc khi biết độ dài của dốc là a và độ cao của đỉnh dốc so với đường nằm ngang là h.
1. Khái niệm tỉ số lượng giác của một góc nhọn
Lời giải:
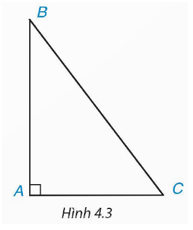
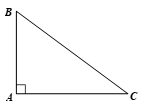
Góc C có cạnh đối là AB và cạnh kề là AC.
Lời giải:
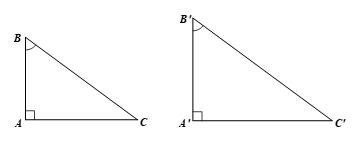
a) Xét ∆ABC và ∆A’B’C’ có:
Do đó ∆ABC ᔕ ∆A’B’C’ (g.g).
b) Từ ∆ABC ᔕ ∆A’B’C’ (câu a), suy ra: (tỉ lệ các cạnh tương ứng).
Từ ta có và (tính chất tỉ lệ thức).
Từ ta có (tính chất tỉ lệ thức).
Từ ta có (tính chất tỉ lệ thức).
Vậy
Lời giải:
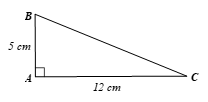
Xét ∆ABC vuông tại A, theo định lí Pythagore, ta có:
BC2 = AB2 + AC2 = 52 + 122 = 169 nên BC = 13 (cm).
Theo định nghĩa của tỉ số lượng giác sin, côsin, tang, côtang ta có:
Lời giải:
Xét ∆ABC vuông tại A, theo định lí Pythagore, ta có:
BC2 = AB2 + AC2 = 52 + 122 = 169 nên BC = 13 (cm).
Theo định nghĩa của tỉ số lượng giác sin, côsin, tang, côtang ta có:
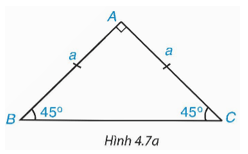
HĐ2 trang 69 Toán 9 Tập 1: Cho tam giác ABC vuông cân tại A và AB = AC = a (H.4.7a).
a) Hãy tính BC và các tỉ số Từ đó suy ra sin45°, cos45°.
b) Hãy tính các tỉ số và Từ đó suy ra tan45°, cot45°.
Lời giải:
Xét ∆ABC vuông tại A, theo định lí Pythagore, ta có:
BC2 = AB2 + AC2 = a2 + a2 = 2a2, suy ra (cm).
∆ABC vuông tại A có AB = AC nên ∆ABC vuông cân tại A nên
a) Ta có: và
Do đó
b) Ta có:
Do đó
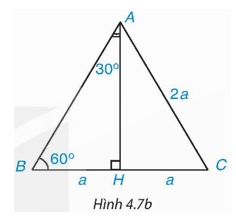
HĐ3 trang 69 Toán 9 Tập 1: Xét tam giác đều ABC có cạnh bằng 2a.
a) Tính đường cao AH của tam giác ABC (H.4.7b).
b) Tính sin30°, cos30°, sin60° và cos60°.
c) Tính tan30°, cot30°, tan60° và cot60°.
Lời giải:
a) Tam giác ABC đều có đường cao AH nên AH cũng là đường trung tuyến của tam giác. Do đó H là trung điểm của BC nên
Xét ∆ABH vuông tại H, theo định lí Pythagore, ta có:
AB2 = AH2 + HB2, suy ra AH2 = AB2 – HB2 = (2a)2 – a2 = 4a2 – a2 = 3a2.
Do đó
b) Tam giác ABC đều nên
Tam giác ABC đều có đường cao AH nên AH cũng là đường phân giác của của tam giác. Do đó
Do đó
c)
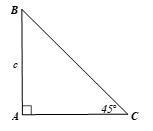
Luyện tập 2 trang 70 Toán 9 Tập 1: Cho tam giác ABC vuông tại A có và AB = c. Tính BC và AC theo c.
Lời giải:
Ta có: suy ra mà tan45° = 1 nên
Tương tự, suy ra mà nên
2. Tỉ số lượng giác của hai góc phụ nhau
Lời giải:
Xét ∆ABC vuông tại C, theo định nghĩa tỉ số lượng giác, ta có:
Từ đó ta có: sinα = cosβ; cosα = sinβ; tanα = cosβ; cotα = tanβ.
Luyện tập 3 trang 70 Toán 9 Tập 1: Hãy giải thích tại sao sin35° = cos55°, tan35° = cot55°.
Lời giải:
Ta có sin35° = cos(90° – 35°) = 55°; tan35° = cot(90° – 35°) = cot55°.
3. Sử dụng máy tính cầm tay tính tỉ số lượng giác của một góc nhọn
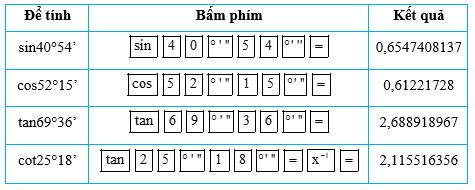
Làm tròn đến chữ số thập phân thứ ba, ta được:
sin40°54’ ≈ 0,655; cos52°15’ ≈ 0,612; tan69°36’ ≈ 2,689; cot25°18’ ≈ 2,116.
Luyện tập 5 trang 72 Toán 9 Tập 1: Dùng MTCT, tìm các góc α (làm tròn đến phút), biết:
d) cotα = 3,253.
Lời giải:
b) Hỏi góc đó có đúng tiêu chuẩn của dốc cho người đi xe lăn không?
Lời giải:
a) Theo định nghĩa tỉ số lượng giác sin, ta có do đó α ≈ 5°44’.
b) Trong các tòa chung cư, người ta thường thiết kế đoạn dốc cho người đi xe lăn với góc dốc bé hơn 6°.
Vì α ≈ 5°44’ < 6° nên góc đó đúng tiêu chuẩn của dốc cho người đi xe lăn.
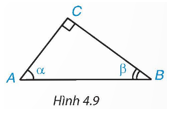
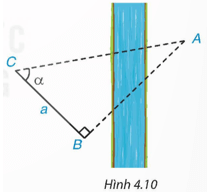
Vuông cho rằng: Không thể tính được AB vì trong tam giác vuông ABC, theo định lí Pythagore, phải biết được hai cạnh mới tính được cạnh thứ ba.
Tròn khẳng định: Với các dữ liệu đã biết là có thể tính được khoảng cách AB rồi.
Em hãy cho biết ý kiến của mình.
Lời giải:
Em đồng ý với ý kiến của bạn Tròn, tức là với các dữ liệu đã biết là có thể tính được khoảng cách AB.
Giải thích: Ta có suy ra AB = BC.tanα = a.tanα.
Với α = 55°, a = 70 m, ta có: AB = 70.tan55° ≈ 99,97 (m).
Bài tập
Lời giải:
a) Xét ∆ABC vuông tại A, theo định lí Pythagore, ta có:
BC2 = AB2 + AC2
Suy ra AC2 = BC2 – AB2 = 172 – 82 = 225.
Do đó AC = 15 cm.
Xét ∆ABC vuông tại A, theo định nghĩa tỉ số lượng giác sin, côsin, tang, cotang và định lí tỉ số lượng giác của hai góc phụ nhau, ta có:
●
●
●
●
b) Xét ∆ABC vuông tại A, theo định lí Pythagore, ta có:
BC2 = AB2 + AC2 = 1,22 + 0,92 = 2,25
Do đó BC = 1,5 cm.
Xét ∆ABC vuông tại A, theo định nghĩa tỉ số lượng giác sin, côsin, tang, cotang và định lí tỉ số lượng giác của hai góc phụ nhau, ta có:
●
●
●
●
Lời giải:
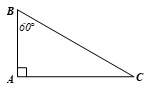
Xét ∆ABC có cạnh kề với góc B là AB = 3 cm. Ta cần tính cạnh đối của góc B là AC.
Theo định nghĩa tỉ số lượng giác tan, ta có
Suy ra (cm).
Vậy cạnh đối của góc nhọn 60° là
Lời giải:
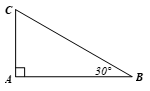
Xét ∆ABC vuông tại A có cạnh đối với góc B là AC = 5 cm. Ta cần tính cạnh huyền của tam giác là BC.
Theo định nghĩa tỉ số lượng giác sin, ta có
Suy ra (cm).
Vậy cạnh huyền của tam giác là 10 cm.
Lời giải:
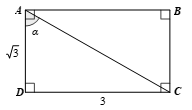
Gọi hình chữ nhật trong bài là hình chữ nhật ABCD với chiều rộng là cạnh chiều dài là cạnh CD = 3, đường chéo AC, góc tạo bởi đường chéo và cạnh ngắn hơn của hình chữ nhật là góc α.
Xét ∆ABC vuông tại D, theo định nghĩa tỉ số lượng giác tan, ta có:
suy ra α = 60°.
Vậy góc giữa đường chéo và cạnh ngắn hơn của hình chữ nhật đã cho là 60°.
sin55°, cos62°, tan57°, cot64°.
Lời giải:
a) Áp dụng định lí tỉ số lượng giác của hai góc phụ nhau, ta có:
⦁ sin55° = cos(90° – 55°) = cos35°;
⦁ cos62° = sin(90° – 62°) = sin28°;
⦁ tan57° = cot(90° – 57°) = cot33°;
⦁ cot64° = tan(90° – 64°) = tan26°.
b) Áp dụng định lí tỉ số lượng giác của hai góc phụ nhau, ta có:
⦁ tan34° – cot56° = tan34° – tan(90° – 56°) = tan34° – tan34° = 0.
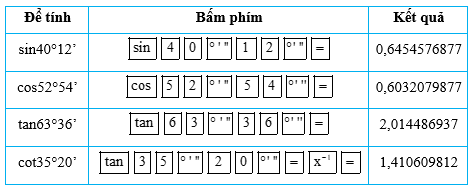
Bài 4.6 trang 73 Toán 9 Tập 1: Dùng MTCT, tính (làm tròn đến chữ số thập phân thứ ba):
Lời giải:
Làm tròn đến chữ số thập phân thứ ba, ta được:
sin40°12’ ≈ 0,645; cos52°54’ ≈ 0,603; tan63°36’ ≈ 2,014; cot35°20’ ≈ 1,411.
Bài 4.7 trang 73 Toán 9 Tập 1: Dùng MTCT, tìm số đo của góc nhọn x (làm tròn đến phút), biết rằng:
Lời giải:
Xem thêm lời giải bài tập Toán 9 sách Kết nối tri thức hay, chi tiết khác:
Bài tập cuối chương 3 trang 65
Bài 12: Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng
Xem thêm các chương trình khác:
- Soạn văn 9 Kết nối tri thức (hay nhất)
- Văn mẫu 9 - Kết nối tri thức
- Tóm tắt tác phẩm Ngữ văn 9 – Kết nối tri thức
- Tác giả tác phẩm Ngữ văn 9 - Kết nối tri thức
- Bố cục tác phẩm Ngữ văn 9 – Kết nối tri thức
- Nội dung chính tác phẩm Ngữ văn 9 – Kết nối tri thức
- Soạn văn 9 Kết nối tri thức (ngắn nhất)
- Bài tập Tiếng Anh 9 Global success theo Unit có đáp án
- Giải sgk Tiếng Anh 9 - Global success
- Trọn bộ Từ vựng Tiếng Anh 9 Global success đầy đủ nhất
- Trọn bộ Ngữ pháp Tiếng Anh 9 Global success đầy đủ nhất
- Giải sbt Tiếng Anh 9 – Global Success
- Giải sgk Khoa học tự nhiên 9 – Kết nối tri thức
- Lý thuyết Khoa học tự nhiên 9 – Kết nối tri thức
- Giải sbt Khoa học tự nhiên 9 – Kết nối tri thức
- Giải sgk Lịch sử 9 – Kết nối tri thức
- Giải sbt Lịch sử 9 – Kết nối tri thức
- Giải sgk Địa lí 9 – Kết nối tri thức
- Giải sbt Địa lí 9 – Kết nối tri thức
- Giải sgk Tin học 9 – Kết nối tri thức
- Giải sbt Tin học 9 – Kết nối tri thức
- Giải sgk Công nghệ 9 – Kết nối tri thức
- Giải sgk Giáo dục công dân 9 – Kết nối tri thức
- Giải sbt Giáo dục công dân 9 – Kết nối tri thức
- Giải sgk Hoạt động trải nghiệm 9 – Kết nối tri thức