Giải Toán 9 (Kết nối tri thức): Luyện tập chung (trang 65)

Giải bài tập Toán 9 Luyện tập chung (trang 65)

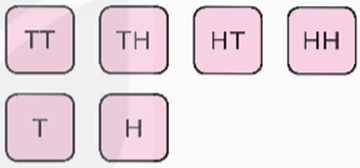
Bài 8.9 trang 65 Toán 9 Tập 2: Có hai túi đựng các tấm thẻ. Túi I đựng 4 tấm thẻ ghi các chữ cái TT, TH, HT và HH. Túi II đựng 2 tấm thẻ ghi các chữ cái T và H. Từ mỗi túi rút ngẫu nhiên ra một tấm thẻ rồi ghép hai thẻ lại với nhau để được ba chữ cái, trong đó thẻ hai chữ cái đặt trước, chẳng hạn tấm thẻ TT ghép với tấm thẻ H được ba chữ cái TTH. Tính xác suất của các biến cố sau:

a) E: “Trong ba chữ cái, có hai chữ H và một chữ T”;

b) F: “Trong ba chữ cái, có nhiều nhất hai chữ T”.

Lời giải:

Phép thử là rút ngẫu nhiên từ mỗi túi một tấm thẻ rồi ghép hai thẻ lại với nhau để được ba chữ cái, trong đó thẻ hai chữ cái đặt trước.

Kết quả của phép thử là abc với ab là hai chữ cái từ túi I và c là chữ cái từ túi II.

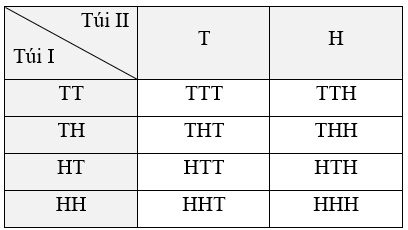
Ta liệt kê tất cả các kết quả có thể của phép thử bằng cách lập bảng như sau:

Mỗi ô trong bảng trên là một kết quả có thể. Các kết quả có thể này là đồng khả năng. Không gian mẫu là Ω = {TTT; TTH; THT; THH; HTT; HTH; HHT; HHH}.

Không gian mẫu có 8 phần tử.

a) Có 3 kết quả thuận lợi cho biến cố E là: THH; HTH; HHT. Vậy $P\left(E\right)=\frac{3}{8}.$

b) Có 7 kết quả thuận lợi cho biến cố E là: TTH; THT; THH; HTT; HTH; HHT; HHH.

Vậy $P\left(F\right)=\frac{7}{8}.$

Bài 8.10 trang 65 Toán 9 Tập 2: Gieo đồng thời hai con xúc xắc cân đối và đồng chất I và II. Tính xác suất của các biến cố sau:

G: “Không có con xúc xắc nào xuất hiện mặt 6 chấm”;

H: “Số chấm xuất hiện trên con xúc xắc I là số lẻ và số chấm xuất hiện trên con xúc xắc II lớn hơn 4”;

K: “Số chấm xuất hiện trên cả hai con xúc xắc lớn hơn 2”.

Lời giải:

Phép thử là gieo đồng thời hai con xúc xắc cân đối và đồng chất I và II.

Kết quả của phép thử là (a, b), trong đó a và b tương ứng là số chấm xuất hiện trên con xúc xắc I và con xúc xắc II.

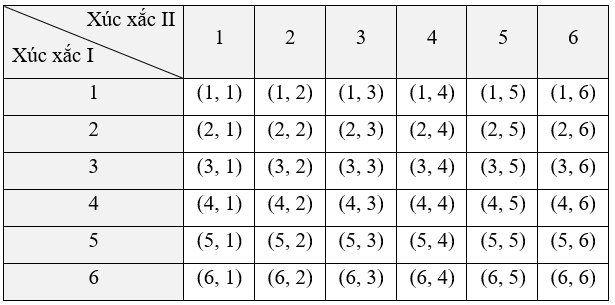
Ta liệt kê được tất cả các kết quả có thể của phép thử bằng cách lập bảng như sau:

Mỗi ô là một kết quả có thể. Không gian mẫu là tập hợp 36 ô của bảng trên. Do đó, không gian mẫu của phép thử là Ω = {(1, 1); (1, 2); (1, 3); …; (5, 6); (6, 6)}.

Tập Ω có 36 phần tử.

Vì gieo đồng thời hai con xúc xắc cân đối, đồng chất nên các kết quả có thể xảy ra là đồng khả năng.

⦁ Có 25 kết quả thuận lợi của biến cố G là: (1, 1); (1, 2); (1, 3); (1, 4); (1, 5); (2, 1); (2, 2); (2, 3); (2, 4); (2, 5); (3, 1); (3, 2); (3, 3); (3, 4); (3, 5); (4, 1); (4, 2); (4, 3); (4, 4); (4, 5); (5, 1); (5, 2); (5, 3); (5, 4); (5, 5). Do đó, $P\left(G\right)=\frac{25}{36}.$

⦁ Có 6 kết quả thuận lợi của biến cố H là: (1, 5); (1, 6); (3, 5); (3, 6); (5, 5); (5, 6). Do đó $P\left(H\right)=\frac{6}{36}=\frac{1}{6}.$

⦁ Có 16 kết quả thuận lợi của biến cố K là: (3, 3); (3, 4); (3, 5); (3, 6); (4, 3); (4, 4); (4, 5); (4, 6); (5, 3); (5, 4); (5, 5); (5, 6); (6, 3); (6, 4); (6, 5); (6, 6). Do đó, $P\left(K\right)=\frac{16}{36}=\frac{4}{9}.$

Bài 8.11 trang 65 Toán 9 Tập 2: Trên một dãy phố có ba quán ăn A, B, C. Hai bạn Văn và Hải mỗi người chọn ngẫu nhiên một quán ăn để ăn trưa.

a) Mô tả không gian mẫu của phép thử.

b) Tính xác suất của các biến cố sau:

E: “Hai bạn cùng vào một quán”;

F: “Cả hai bạn không chọn quán C”;

G: “Có ít nhất một bạn chọn quán B”.

Lời giải:

a) Phép thử là hai bạn Văn và Hải mỗi người chọn ngẫu nhiên một quán ăn trong ba quán ăn A, B, C để ăn trưa.

Kết quả của phép thử là (a, b), trong đó a và b tương ứng là quán ăn mà bạn Văn và Hải lựa chọn.

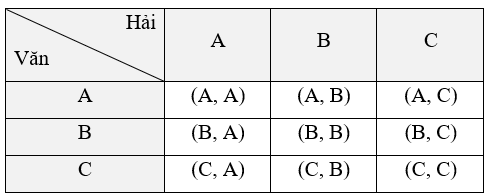
Ta liệt kê được tất cả các kết quả có thể của phép thử bằng cách lập bảng như sau:

Mỗi ô là một kết quả có thể. Không gian mẫu là tập hợp 9 ô của bảng trên. Do đó, không gian mẫu của phép thử là Ω = {(A, A); (A, B); (A, C); (B, A); (B, B); (B, C); (C, A); (C, B); (C, C)}.

Tập Ω có 9 phần tử.

b) Vì hai bạn Văn và Hải mỗi người chọn ngẫu nhiên một quán ăn để ăn trưa nên các kết quả có thể của phép thử là đồng khả năng.

⦁ Có 3 kết quả thuận lợi của biến cố E là: (A, A); (B, B); (C, C). Do đó, $P\left(E\right)=\frac{3}{9}=\frac{1}{3}.$

⦁ Có 4 kết quả thuận lợi của biến cố F là: (A, A); (A, B); (B, A); (B, B). Do đó, $P\left(F\right)=\frac{4}{9}.$

⦁ Có 5 kết quả thuận lợi của biến cố G là: (A, B); (B, A); (B, B); (B, C); (C, B). Do đó, $P\left(G\right)=\frac{5}{9}.$

Xem thêm Lời giải bài tập Toán 9 Kết nối tri thức hay, chi tiết khác:

Bài tập cuối chương 8

Bài 27: Góc nội tiếp

Bài 28: Đường tròn ngoại tiếp và đường tròn nội tiếp của một tam giác

Luyện tập chung (trang 79)

Bài 29: Tứ giác nội tiếp