Giải Toán 9 Bài 32 (Kết nối tri thức): Hình cầu

Giải bài tập Toán 9 Bài 32: Hình cầu

Mở đầu trang 101 Toán 9 Tập 2: Quả bóng đá theo tiêu chuẩn FIFA (Liên đoàn Bóng đá Quốc tế) có dạng hình cầu với đường kính 22 cm (H.10.18). Khi bơm căng quả bóng thì thể tích quả bóng bằng bao nhiêu?

Lời giải:

Sau bài học này ta giải quyết được bài toán như sau:

Bán kính quả bóng là: R = $\frac{22}{2}$ = 11 (cm).

Thể tích quả bóng là: $V=\frac{4}{3}\pi R^3=\frac{4}{3}\pi \cdot {11}^3=\frac{5324}{3}\pi \left(c{m}^3\right).$

Vậy khi bơm căng quả bóng thì thể tích quả bóng bằng $\frac{5324}{3}\pi c{m}^3$.

1. Mặt cầu và hình cầu

Câu hỏi trang 102 Toán 9 Tập 2: Tìm một vài hình ảnh của hình cầu, mặt cầu trong thực tế.

Lời giải:

Một vài hình ảnh của hình cầu, mặt cầu trong thực tế là: quả địa cầu, quả bóng chuyền, đèn gắn tường,...

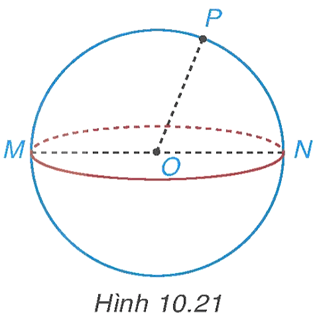
Luyện tập 1 trang 102 Toán 9 Tập 2: Kể tên các bán kính còn lại của hình cầu có trong Hình 10.21.

Lời giải:

Bán kính còn lại của mặt cầu có trong Hình 10.21 là OM, ON.

HĐ1 trang 102 Toán 9 Tập 2: Sọ dừa được xem là có dạng hình cầu. Người ta cắt sọ dừa khô để làm gáo dừa (H.10.22a). Em thấy miệng gáo có dạng hình gì?

Lời giải:

Miệng gáo có dạng hình tròn.

HĐ2 trang 102 Toán 9 Tập 2: Khi cắt đôi một quả cam có dạng hình cầu (H.10.22b), em thấy mặt cắt có dạng hình gì?

Lời giải:

Khi cắt đôi một quả cam có dạng hình cầu thì mặt cắt của quả cam có dạng hình tròn.

Luyện tập 2 trang 103 Toán 9 Tập 2: Khi cắt một hình cầu bởi một mặt phẳng đi qua tâm của hình cầu đó được một hình tròn có diện tích 25π cm². Tính bán kính của hình cầu.

Lời giải:

Do cắt hình cầu bởi một mặt phẳng đi qua tâm của hình cầu nên bán kính của hình tròn bằng bán kính của hình cầu.

Gọi R là bán kính của hình cầu.

Khi đó ta có: πR² = 25π, suy ra R² = 25 nên R = 5 cm.

2. Diện tích mặt cầu và thể tích hình cầu

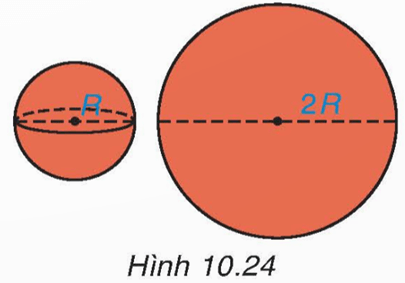
HĐ3 trang 103 Toán 9 Tập 2: Người ta thấy rằng lượng sơn cần dùng để sơn kín một mặt cầu bán kính R bằng với lượng sơn cần dùng để sơn kín một hình tròn bán kính 2R (khi độ dày của lớp sơn như nhau) (H.10.24). Từ đó, em hãy dự đoán công thức tính diện tích mặt cầu bán kính R.

Lời giải:

Diện tích hình tròn bán kính 2R là: S = π . (2R)² = 4πR².

Ta thấy lượng sơn cần dùng để sơn kín một mặt cầu bán kính R bằng với lượng sơn cần dùng để sơn kín một hình tròn bán kính 2R.

Do đó, ta dự đoán công thức tính diện tích mặt cầu là bán kính R là: S = 4πR².

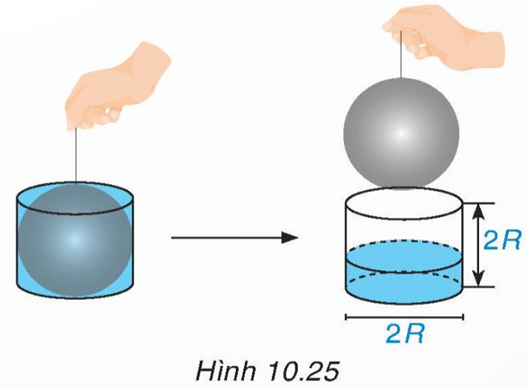
HĐ4 trang 103 Toán 9 Tập 2: Sử dụng một hình cầu bán kính R và một cốc thủy tinh có dạng hình trụ bán kính đáy R, chiều cao 2R. Ban đầu để hình cầu nằm khít trong chiếc cốc có đầy nước.

Ta nhấc hình cầu ra khỏi cốc thủy tinh hình trụ (H.10.25).

Đo độ cao cột nước còn lại trong chiếc cốc, ta thấy độ cao này chỉ bằng $\frac{1}{3}$ chiều cao của chiếc cốc hình trụ. Từ đó, em hãy dự đoán công thức tính thể tích hình cầu bán kính R.

Lời giải:

Thể tích của nước trong cốc khi hình cầu trong cốc là:

V₁ = πR² . 2R = 2πR³.

Thể tích của nước trong cốc khi bỏ hình cầu ra ngoài là:

$V_2=\pi R^2\cdot \frac{1}{3}\cdot 2R=\frac{2}{3}\pi R^3.$

Thể tích của hình cầu là: $V=V_1-V_2=2\pi R^3-\frac{2}{3}\pi R^3=\frac{4}{3}\pi R^3.$

Dự đoán công thức tính thể tích hình cầu bán kính R là: $V=\frac{4}{3}\pi R^3.$

Vận dụng 1 trang 104 Toán 9 Tập 2: Em hãy trả lời câu hỏi của tình huống mở đầu.

Lời giải:

Bán kính quả bóng là: $R=\frac{22}{2}=11\left(cm\right)$.

Thể tích quả bóng là: $V=\frac{4}{3}\pi R^3=\frac{4}{3}\pi \cdot {11}^3=\frac{5324}{3}\pi \left(c{m}^3\right).$

Vậy khi bơm căng quả bóng thì thể tích quả bóng bằng $\frac{5324}{3}\pi c{m}^3$.

Vận dụng 2 trang 105 Toán 9 Tập 2: Khinh khí cầu đầu tiên được phát minh bởi anh em nhà Montgolfier (người Pháp) vào năm 1782. Chuyến bay đầu tiên của hai anh em trên khinh khí cầu được thực hiện vào ngày 4 tháng 6 năm 1783 trên bầu trời Place des Cordeliers ở Annonay (nước Pháp) (theo cand.com.vn). Giả sử một khinh khí cầu có dạng hình cầu với đường kính bằng 11 m. Tính diện tích khinh khí cầu đó (làm tròn kết quả đến hàng đơn vị của m²).

Lời giải:

Bán kính khinh khí cầu là R = $\frac{11}{2}$m.

Diện tích khinh khí cầu là:

$S=4\pi R^2=4\pi \cdot {\left(\frac{11}{2}\right)}^2=121\pi \approx 380\left(m^2\right).$

Vậy diện tích khinh khí cầu đó khoảng 380 m².

Bài 10.7 trang 105 Toán 9 Tập 2: Thay dấu “?” bằng giá trị thích hợp và hoàn thành bảng sau vào vở:

Lời giải:

Hình vẽ trong bảng trên là hình cầu:

• Xét hình cầu có bán kính là R = 3 cm, ta có:

Diện tích mặt cầu là: S = 4πR² = 4π . 3² = 36π (cm²).

Thể tích mặt cầu là: $V=\frac{4}{3}\pi R^3=\frac{4}{3}\pi \cdot 3^3=36\pi \left(c{m}^3\right)$.

• Xét hình cầu có diện tích mặt cầu 100π cm², ta có:

Bán kính hình cầu là: $R^2=\frac{S}{4\pi }=\frac{100\pi }{4\pi }=25\Rightarrow R=5\left(cm\right).$

Thể tích mặt cầu là: $V=\frac{4}{3}\pi R^3=\frac{4}{3}\pi \cdot 5^3=\frac{500}{3}\pi \left(c{m}^3\right)$

• Xét hình cầu có thể tích mặt cầu 972π cm³, ta có:

Bán kính hình cầu là: $R^3=\frac{3V}{4\pi }=\frac{3\cdot 972\pi }{4\pi }=729\Rightarrow R=9\left(cm\right).$

Diện tích mặt cầu là: S = 4πR² = 4π . 9² = 324π (cm²).

Từ đó, ta có điền vào bảng như sau:

Bài 10.8 trang 105 Toán 9 Tập 2: Một cốc đựng ba viên kem có dạng hình cầu, mỗi viên đều có bán kính bằng 3 cm. Tính thể tích của kem đựng trong cốc (làm tròn kết quả đến hàng đơn vị của cm³).

Lời giải:

Thể tích của ba viên kem là:

$3\cdot \frac{4}{3}\pi \cdot 3^3=108\pi \left(c{m}^3\right)\approx 339\left(c{m}^3\right)$.

Vậy thể tích của kem đựng trong cốc khoảng 339 cm³.

Bài 10.9 trang 105 Toán 9 Tập 2: Một quả bóng đá có chu vi của đường tròn lớn bằng 68,5 cm. Quả bóng được ghép nối bởi các miếng da hình lục giác đều màu trắng và đen, mỗi miếng có diện tích bằng 49,83 cm². Hỏi cần ít nhất bao nhiêu miếng da để làm quả bóng trên? (Coi phần mép khâu không đáng kể).

Lời giải:

Bán kính đường tròn lớn chính là bán kính quả bóng.

Bán kính quả bóng là: $R=68,5:\pi :2=\frac{137}{4\pi }\left(cm\right).$

Diện tích mặt quả bóng là:

$S=4\pi R^2=4\pi \cdot {\left(\frac{137}{4\pi }\right)}^2=\frac{18769}{4\pi }\left(c{m}^2\right).$

Số miếng da cần dùng là:

$\frac{18769}{4\pi }:49,83\approx 29,97$ (miếng).

Vậy cần ít nhất 30 miếng da để làm quả bóng trên.

Bài 10.10 trang 105 Toán 9 Tập 2: Hằng năm cứ dịp Tết đến Xuân về, dân làng Thúy Lĩnh, phường Lĩnh Nam, quận Hoàng Mai, Hà Nội lại tổ chức lễ hội vật cầu truyền thống. Trong lễ hội có sử dụng một quả cầu được tiện bằng gỗ, đường kính khoảng 35 cm, sơn đỏ mặt ngoài. Tính diện tích mặt ngoài của quả cầu gỗ nói trên.

Lời giải:

Bán kính hình cầu là: $\frac{35}{2}=17,5\left(cm\right).$

Diện tích mặt ngoài của quả cầu gỗ là:

$S=4\pi R^2=4\pi \cdot 17,5^2=1225\pi \left(c{m}^2\right).$

Vậy diện tích mặt ngoài của quả cầu gỗ 1 225 cm².

Xem thêm Lời giải bài tập Toán 9 Kết nối tri thức hay, chi tiết khác:

Luyện tập chung

Bài tập cuối chương 10

Giải phương trình hệ phương trình và vẽ đồ thị hàm số với phần mềm GeoGebra

Vẽ hình đơn giản với phần mềm GeoGebra

Xác định tần số tần số tương đối vẽ các biểu đồ biểu diễn bảng tần số tần số tương đối bằng Excel