Nội dung bài viết

    Xem thêm

    Toán 9 (Kết nối tri thức) Tính chiều cao và xác định khoảng cách

    Với giải bài tập Toán lớp 9 Tính chiều cao và xác định khoảng cách sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 9.

    1 529 29/07/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 9 Tính chiều cao và xác định khoảng cách

    Nhiệm vụ 1 trang 116 Toán 9 Tập 1: Xác định chiều cao

    Mục tiêu: Xác định chiều cao của một tòa nhà trong trường mà không thực hiện đo trực tiếp.

    Chuẩn bị, xây dựng ý tưởng: Nhóm thảo luận, xây dựng ý tưởng thực hiện nhiệm vụ và phân công nhiệm vụ.

    Thực hiện nhiệm vụ:

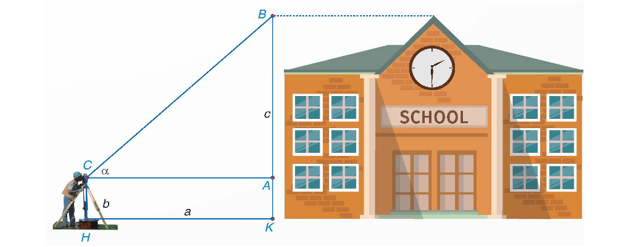
    Nhiệm vụ 1 trang 116 Toán 9 Kết nối tri thức Tập 1 | Giải Toán 9

    Bước 1. Đặt giác kế thẳng đứng cách chân tòa nhà một khoảng cách a mét, giả sử chiều cao tòa nhà của giác kế là b mét. Quay ống ngắm của giác kế sao cho ta nhìn thấy đỉnh B của tòa nhà. Đọc trên giác kế số đo α của góc BCA.

    Bước 2. Sử dụng hệ thức giữa cạnh và góc trong ∆ABC vuông tại A và máy tính bỏ túi ta tính được c = AB = AC . tan α.

    Bước 3. Tính chiều cao của tòa nhà là b + c (m).

    Lời giải:

    HS thực hành đo khoảng cách a mét, chiều cao giác kế b mét, số đo α.

    Từ đó, tính chiều cao của tòa nhà là b + c (m).

    Báo cáo kết quả: Sau khi thực hiện đo đạc và tính toán, nhóm trình bày trước và tổ chức đánh giá nhiệm vụ.

    Nhiệm vụ 2 trang 117 Toán 9 Tập 1: Xác định khoảng cách

    Mục tiêu: Xác định khoảng cách giữa hai vị trí giả định trên sân trường (như hai điểm bên hai bờ sông). Vị trí hai điểm giả định cho giáo viên xác định.

    Chuẩn bị, xây dựng ý tưởng: Nhóm thảo luận, xây dựng ý tưởng thực hiện nhiệm vụ và phân công nhiệm vụ.

    Thực hiện nhiệm vụ: Để đo khoảng cách giữa hai điểm A và B (giữa hai điểm này có vật cản hoặc chỉ đến được một trong hai vị trí A, B), ta thực hiện như sau:

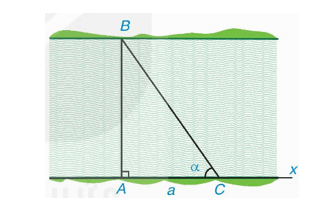
    Nhiệm vụ 2 trang 117 Toán 9 Kết nối tri thức Tập 1 | Giải Toán 9

    Bước 1. Từ điểm A ta kẻ Ax ⊥ AB. Trên tia Ax lấy điểm C sao cho AC = a mét. Tại vị trí C sử dụng giác kế ngắm tới điểm B. Đọc trên giác kế số đo góc α của góc ACB.

    Bước 2. Sử dụng hệ thức giữa cạnh và góc trong ∆ABC vuông tại A và MTCT ta tính được AB = AC . tan α = α tan α.

    Lời giải:

    HS thực hành theo các bước ở đề bài và sử dụng MTCT để tính độ dài AB, đó chính là khoảng cách giữa hai điểm A và B.

    Báo cáo kết quả: Sau khi thực hiện đo đạc và tính toán, nhóm trình bày trước và tổ chức đánh giá nhiệm vụ.

    Tham khảo các loạt bài Toán 9 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 529 29/07/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: