Toán 9 Bài 13 (Kết nối tri thức): Mở đầu về đường tròn

Giải Toán 9 Bài 13: Mở đầu về đường tròn

Mở đầu trang 83 Toán 9 Tập 1: Bạn Oanh có một mảnh giấy hình tròn nhưng không còn dấu vết của tâm. Theo em, Oanh làm thế nào để tìm lại được tâm của hình tròn đó.

Lời giải:

Sau bài học này ta giải quyết được bài toán như sau:

Gấp đôi hình tròn sao cho mép giấy của chúng đè khít lên nhau, ta miết phần ngăn cách hai nửa hình tròn ta được một đường kính.

Tiếp theo ta mở tờ giấy và gấp theo hướng khác và các mép giấy của hình tròn cũng đè khít lên nhau. Từ đó, xác định được đường kính mới.

Hai đường kính này cắt nhau tại một điểm chính là tâm của hình tròn.

1. Đường tròn

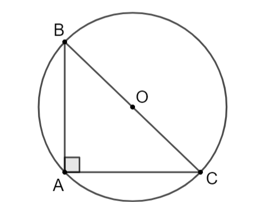
Luyện tập 1 trang 84 Toán 9 Tập 1: Cho tam giác ABC vuông tại A. Chứng minh rằng điểm A thuộc đường tròn đường kính BC.

Lời giải:

Gọi O là trung điểm của BC.

Ta có AO là trung tuyến ứng với cạnh huyền nên $OA=OB=OC=\frac{1}{2}BC.$

Suy ra A, B, C cùng thuộc đường tròn bán kính OA.

Tâm O là trung điểm của BC nên BC là đường kính.

Vậy điểm A thuộc đường tròn đường kính BC.

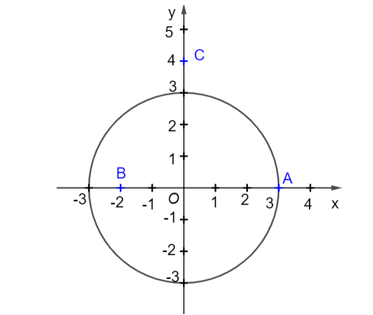
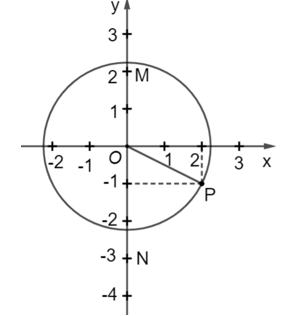
Vận dụng 1 trang 84 Toán 9 Tập 1: Trong mặt phẳng tọa độ Oxy, cho các điểm A(3; 0), B(−2; 0), C(0; 4). Vẽ hình và cho biết trong các điểm đã cho, điểm nào nằm trên, điểm nào nằm trong, điểm nào nằm ngoài đường tròn (O; 3)?

Lời giải:

Ta có: OA = 3 nên điểm A nằm trên đường tròn (O; 3).

OB = 2 < 3 nên điểm B nằm trong đường tròn (O; 3).

OC = 4 > 3 nên điểm C nằm ngoài đường tròn (O; 3).

Vậy trong các điểm đã cho, điểm A nằm trên, điểm B nằm trong, điểm C nằm ngoài đường tròn (O; 3).

2. Tính đối xứng của đường tròn

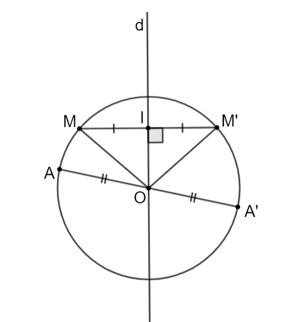
HĐ trang 85 Toán 9 Tập 1: Chứng minh rằng nếu một điểm thuộc đường tròn (O) thì:

a) Điểm đối xứng với nó qua tâm O cũng thuộc (O).

b) Điểm đối xứng với nó qua một đường thẳng d tùy ý đi qua O cũng thuộc (O).

Lời giải:

a) Lấy điểm A bất kì thuộc (O).

Gọi A' là điểm đối xứng với A qua O.

Khi đó: O là trung điểm của AA' hay OA = OA' = R.

Suy ra A' cũng thuộc đường tròn (O).

b) Lấy điểm M bất kì thuộc (O).

Gọi M' là điểm đối xứng với M qua d.

Gọi I là giao điểm của d với MM'.

Khi đó: MM' ⊥ OI tại M hay $\widehat{OIM}=\widehat{OI{M}^{\text{'}}}=90°$ .

Xét ∆OIM và ∆OIM' có:

OI chung

$\widehat{OIM}=\widehat{OI{M}^{\text{'}}}=90°$

IM = IM'

Do đó ∆OIM = ∆OIM' (c.g.c).

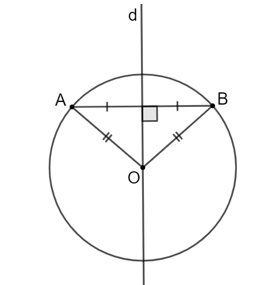
Luyện tập 2 trang 86 Toán 9 Tập 1: Cho đường tròn tâm O và hai điểm A, B thuộc (O). Gọi d là đường trung trực của đoạn AB. Chứng minh rằng d là một trục đối xứng của (O).

Lời giải:

Vì hai điểm A, B thuộc (O) nên OA = OB.

Mà d là đường trung trực của đoạn AB nên nên O thuộc d.

Hay đường thẳng d đi qua tâm O của đường tròn.

Vậy d là một trục đối xứng của (O).

Vận dụng 2 trang 86 Toán 9 Tập 1: Trở lại tình huống mở đầu, bằng cách gấp mảnh giấy hình tròn theo hai cách khác nhau, Oanh có thể tìm được tâm của hình tròn. Em hãy làm thử xem.

Lời giải:

Gấp đôi hình tròn sao cho mép giấy của chúng đè khít lên nhau, ta miết phần ngăn cách hai nửa hình tròn ta được một đường kính.

Tiếp theo ta mở tờ giấy và gấp theo hướng khác và các mép giấy của hình tròn cũng đè khít lên nhau. Từ đó, xác định được đường kính mới.

Hai đường kính này cắt nhau tại một điểm chính là tâm của hình tròn.

Bài tập

Bài 5.1 trang 86 Toán 9 Tập 1: Trong mặt phẳng tọa độ Oxy, cho các điểm M (0; 2), N (0; −3) và P(2; −1). Vẽ hình và cho biết trong các điểm đã cho, điểm nào nằm trên, điểm nào nằm trong, điểm nào nằm ngoài đường tròn $\left(O;\sqrt{5}\right)?$ Vì sao?

Lời giải:

Ta có: $OM=2<\sqrt{5}$ nên điểm M nằm trong đường tròn $\left(O;\sqrt{5}\right)$ .

$ON=3>\sqrt{5}$ nên điểm N nằm ngoài đường tròn $\left(O;\sqrt{5}\right)$ .

Mặt khác, OP² = 2² + 1² = 5 (theo định lí Pythagore).

Suy ra $OP=\sqrt{5}$ nên điểm P nằm trên đường tròn $\left(O;\sqrt{5}\right)$ .

Vậy trong các điểm đã cho, điểm P nằm trên, điểm M nằm trong, điểm N nằm ngoài đường tròn $\left(O;\sqrt{5}\right)$ .

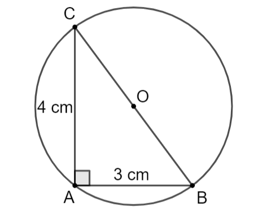
Bài 5.2 trang 86 Toán 9 Tập 1: Cho tam giác ABC vuông tại A có AB = 3 cm, AC = 4 cm. Chứng minh rằng các điểm A, B, C thuộc cùng một đường tròn. Tính bán kính của đường tròn đó.

Lời giải:

Gọi O là trung điểm của BC.

Ta có AO là trung tuyến ứng với cạnh huyền nên $OA=OB=OC=\frac{1}{2}BC.$

Suy ra A, B, C cùng thuộc đường tròn bán kính OA.

Tâm O là trung điểm của BC nên BC là đường kính.

Do đó, các điểm A, B, C thuộc cùng một đường tròn.

Xét tam giác ABC vuông tại A, áp dụng định lí Pythagore, ta có:

BC² = AB² + AC² = 3² + 4² = 25.

Suy ra BC = 5 cm.

Khi đó $OA=\frac{1}{2}BC=\frac{5}{2}=2,5\text{\hspace{0.17em}\hspace{0.17em}(cm)}.$

Vậy các điểm A, B, C thuộc cùng một đường tròn và có bán kính là 2,5 cm.

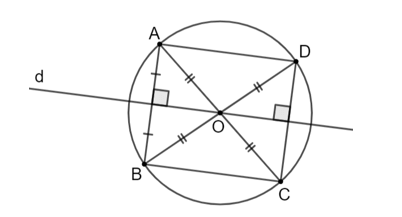
Bài 5.3 trang 86 Toán 9 Tập 1: Cho đường tròn (O), đường thẳng d đi qua O và điểm A thuộc (O) nhưng không thuộc d. Gọi B là điểm đối xứng với A qua d, C và D lần lượt là điểm đối xứng với A và B qua O.

a) Ba điểm B, C và D có thuộc (O) hay không? Vì sao?

b) Chứng minh tứ giác ABCD là hình chữ nhật.

c) Chứng minh rằng C và D đối xứng với nhau qua d.

Lời giải:

a) Ta có d là là đường thẳng đi qua tâm O nên d là trục đối xứng của đường tròn.

Vì A thuộc (O) và B là điểm đối xứng của A qua d nên B cũng thuộc (O).

Vì C, D lần lượt là điểm đối xứng của A, B qua O nên C, D cũng thuộc (O).

b) C đối xứng với A qua O nên O là trung điểm của AC.

D đối xứng với B qua O nên O là trung điểm của BD.

Tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại trung điểm O của mỗi đường.

Mà BD = CD (bằng 2 lần bán kính (O)).

Do đó, tứ giác ABCD là hình chữ nhật.

c) Vì ABCD là hình chữ nhật nên AB // CD, mà AB ⊥ d nên d ⊥ CD.

Xét tam giác OCD có OC = OD nên tam giác OCD cân tại O.

Mà đường thẳng d là đường cao của tam giác OCD nên d cũng là trung trực của CD. Hay C và D đối xứng nhau qua đường thẳng d.

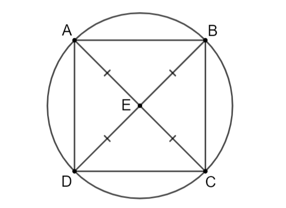
Bài 5.4 trang 86 Toán 9 Tập 1: Cho hình vuông ABCD có E là giao điểm của hai đường chéo.

a) Chứng minh rằng chỉ có một đường tròn đi qua bốn điểm A, B, C và D. Xác định tâm đối xứng và chỉ ra hai trục đối xứng của đường tròn đó.

b) Tính bán kính của đường tròn ở câu a, biết rằng hình vuông có cạnh bằng 3 cm.

Lời giải:

a) Do ABCD là hình vuông nên AC = BD và E là trung điểm của AC và BD.

Suy ra: EA = EB = EC = ED.

Do đó các điểm A, B, C, D cùng thuộc một đường tròn hay chỉ có một đường tròn duy nhất đi qua bốn điểm này.

Đường tròn (E) có tâm E là tâm đối xứng và có hai trục đối xứng là AC và BD.

b) Hình vuông có cạnh bằng 3 cm nên AB = BC = CD = DA = 3 cm.

Áp dụng định lý Pythagore vào tam giác ABC vuông tại B, ta có:

AC² = AB² + BC² = 3² + 3² = 18.

Suy ra $AC=3\sqrt{2}\text{\hspace{0.17em}\hspace{0.17em}cm}$ .

Khi đó $EA=\frac{AC}{2}=\frac{3\sqrt{2}}{2}\text{\hspace{0.17em}\hspace{0.17em}(cm)}.$

Vậy bán kính của đường tròn ở câu a là $EA=\frac{3\sqrt{2}}{2}\text{\hspace{0.17em}\hspace{0.17em}cm}.$