Nội dung bài viết

    Xem thêm

    Toán 9 Bài 1 (Kết nối tri thức): Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn

    Với giải bài tập Toán lớp 9 Bài 1: Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn sách Kết nối tri thức hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 9 Bài 1.

    1 2,953 20/04/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Giải Toán 9 Bài 1: Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn

    Giải Toán 9 trang 6 Tập 1

    HĐ 2 trang 6 Toán 9 Tập 1: Tương tự, hãy viết hệ thức với hai biến x và y biểu thị giả thiết cho bởi các câu thơ thứ ba, thứ tư và thứ năm.

    Quýt, cam mười bảy quả tươi

    Đem chia cho một trăm người cùng vui.

    Chia ba mỗi quả quýt rồi,

    Còn cam, mỗi quả chia mười vừa xinh.

    Trăm người, trăm miếng ngọt lành.

    Quýt, cam mỗi loại tính rành là bao?

    Toán 9 Bài 1 (Kết nối tri thức): Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn (ảnh 1)

    Lời giải:

    Hệ thức liên hệ giữa x và y qua các câu thơ thứ ba, thứ tư và thứ năm là 3x+10y=100.

    Luyện tập 1 trang 6 Toán 9 Tập 1: Hãy viết một phương trình bậc nhất hai ẩn và chỉ ra một nghiệm của nó.

    Lời giải:

    Ta có 2x−y=5 là một phương trình bậc nhất hai ẩn.

    Cặp số (3;1) là một nghiệm của phương trình 2x−y=5 vì 2.3−1=5. (luôn đúng).

    Luyện tập 2 trang 8 Toán 9 Tập 1: Viết nghiệm và biểu diễn hình học tất cả các nghiệm của mỗi phương trình bậc nhất hai ẩn sau:

    a) 2x−3y=5;

    b) 0x+y=3;

    c) x+0y=−2.

    Lời giải:

    a) 2x−3y=5;

    Ta có y=2x+53=2x3+53 nên mỗi cặp số (x;2x3+53) với x∈R tùy ý là một nghiệm của phương trình 2x−3y=5.

    Biểu diễn hình học tất cả các nghiệm của phương trình 2x−3y=5.

    Cho x=0⇒y=−53⇒A(0;−53)

    y=0⇒x=52⇒B(52;0)

    Đường thẳng 2x−3y=5 đi qua hai điểm A và B

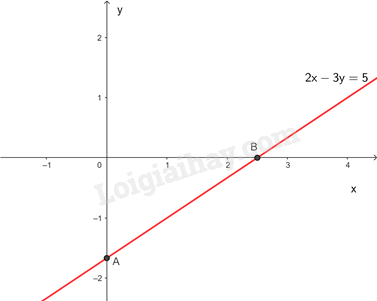
    Toán 9 Bài 1 (Kết nối tri thức): Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn (ảnh 1)

    Các nghiệm là tọa độ của một điểm thuộc đường thẳng 2x−3y=5.

    b) 0x+y=3;

    Ta có 0x+y=3 rút gọn thành y=3 nên phương trình có nghiệm là (x;3) với x∈R tùy ý.

    Biểu diễn hình học tất cả các nghiệm của phương trình 0x+y=3

    Cho x=0⇒y=3⇒A(0;3)

    x=1⇒y=3⇒B(1;3)

    Đường thẳng 0x+y=3 đi qua hai điểm A và B

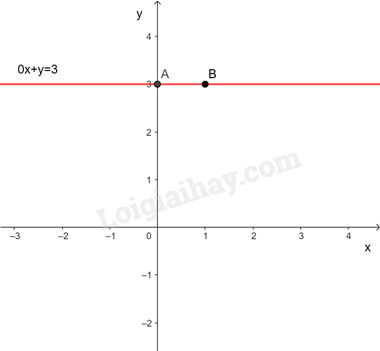
    Toán 9 Bài 1 (Kết nối tri thức): Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn (ảnh 1)

    Các nghiệm là tọa độ của một điểm thuộc đường thẳng 0x+y=3.

    c) x+0y=−2.

    Ta có x+0y=−2 rút gọn thành x=−2 nên phương trình có nghiệm là (−2;y) với y∈R tùy ý.

    Biểu diễn hình học tất cả các nghiệm của phương trình x+0y=−2

    Cho y=0⇒x=−2⇒A(−2;0)

    y=1⇒x=−2⇒B(−2;1)

    Đường thẳng x+0y=−2 đi qua hai điểm A và B

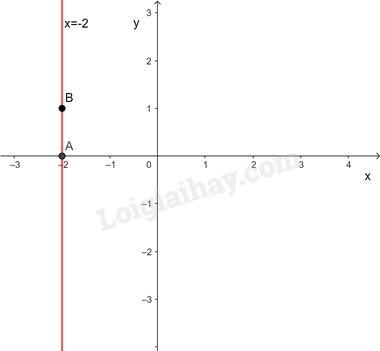
    Toán 9 Bài 1 (Kết nối tri thức): Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn (ảnh 1)

    Các nghiệm là tọa độ của một điểm thuộc đường thẳng x+0y=−2.

    Giải Toán 9 trang 9 Tập 1

    Luyện tập 3 trang 9 Toán 9 Tập 1: Trong hai cặp số (0;−2) và (2;−1), cặp số nào là nghiệm của hệ phương trình {x−2y=44x+3y=5?

    Lời giải:

    Thay (0;−2) vào hệ đã cho ta có:

    {0−2.(−2)=44.0+3(−2)=5 (vô lí)

    Nên (0;−2) không là nghiệm của hệ phương trình đã cho.

    Thay (2;−1) vào hệ đã cho ta có:

    {2−2.(−1)=44.2+3(−1)=5 (luôn đúng)

    Nên (2;−1) là nghiệm của hệ phương trình đã cho.

    Vận dụng trang 9 Toán 9 Tập 1: Xét bài toán cổ trong tình huống mở đầu. Gọi x là số cam, y là số quýt cần tính (x;y∈N∗), ta có hệ phương trình bậc nhất hai ẩn sau:

    {x+y=1710x+3y=100

    Trong hai cặp số (10;7) và (7;10), cặp số nào là nghiệm của hệ phương trỉnh trên? Từ đó cho biết phương án về số cam và số quýt thỏa mãn yêu cầu của bài toán cổ.

    Lời giải:

    Thay (10;7) vào hệ đã cho ta có:

    {10+7=1710.10+3.7=100 (vô lí)

    Nên (10;7) không là nghiệm của hệ phương trình đã cho.

    Thay (7;10) vào hệ đã cho ta có:

    {7+10=1710.7+3.10=100 (luôn đúng)

    Nên (7;10) là nghiệm của hệ phương trình đã cho.

    Vậy số quả quýt là 7 quả, số quả cam là 10 quả.

    Bài tập

    Giải Toán 9 trang 10 Tập 1

    Bài 1.1 trang 10 Toán 9 Tập 1: Phương trình nào sau đây là phương trình bậc nhất hai ẩn, vì sao?

    a) 5x−8y=0;

    b) 4x+0y=−2;

    c) 0x+0y=1;

    d) 0x−3y=9.

    Lời giải:

    a) Là phương trình bậc nhất vì phương trình có dạng ax+by=c và a=5;b=−8 thỏa mãn điều kiện a≠0 hoặc b≠0.

    b) Là phương trình bậc nhất vì phương trình có dạng ax+by=c và a=4;b=0 thỏa mãn điều kiện a≠0 hoặc b≠0.

    c) Không là phương trình bậc nhất vì phương trình có hệ số a=0;b=0 không thỏa mãn điều kiện a≠0 hoặc b≠0.

    d) Là phương trình bậc nhất vì phương trình có dạng ax+by=c và a=0;b=−3 thỏa mãn điều kiện a≠0 hoặc b≠0.

    Bài 1.2 trang 10 Toán 9 Tập 1:

    a) Tìm giá trị thích hợp thay cho dấu “?” trong bảng sau rồi cho biết 6 nghiệm của phương trình 2x−y=1:

    Toán 9 Bài 1 (Kết nối tri thức): Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn (ảnh 1)

    b) Viết nghiệm tổng quát của phương trình đã cho.

    Lời giải:

    a)

    Toán 9 Bài 1 (Kết nối tri thức): Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn (ảnh 1)

    Các cặp nghiệm của phương trình y=2x−1 là: (−1;−3);(−0,5;−2);(0;−1);(0,5;0);(1;1);(2;3).

    b) Ta có: 2x−y=1⇒y=2x−1 nên cặp số (x;2x−1) với x∈R tùy ý là nghiệm tổng quát của phương trình 2x−y=1.

    Lời giải:

    a) 2x−y=3

    Ta có y=2x−3 nên mỗi cặp số (x;2x−3) với x∈R tùy ý là một nghiệm của phương trình 2x−y=3.

    Biểu diễn hình học tất cả các nghiệm của phương trình 2x−y=3

    Cho x=0⇒y=−3⇒A(0;−3)

    y=0⇒x=32⇒B(32;0)

    Đường thẳng 2x−y=3 đi qua hai điểm A và B

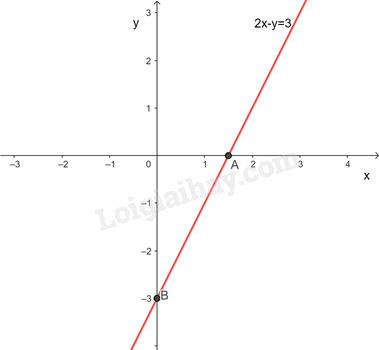
    Toán 9 Bài 1 (Kết nối tri thức): Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn (ảnh 1)

    b) 0x+2y=−4

    Ta có 0x+2y=−4⇒y=−2 nên mỗi cặp số (x;−2) với x∈R tùy ý là một nghiệm của phương trình 0x+2y=−4

    Biểu diễn hình học tất cả các nghiệm của phương trình 0x+2y=−4

    Cho x=0⇒y=−2⇒A(0;−2)

    x=1⇒y=−2⇒B(1;−2)

    Đường thẳng 0x+2y=−4 đi qua hai điểm A và B

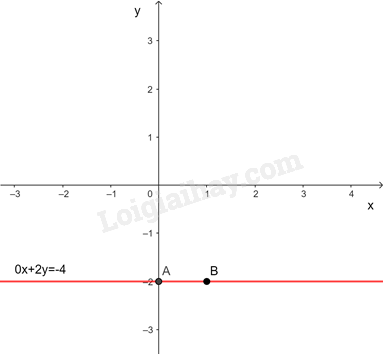
    Toán 9 Bài 1 (Kết nối tri thức): Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn (ảnh 1)

    c) 3x+0y=5

    Ta có 3x+0y=5⇒x=53 nên mỗi cặp số (53;y) với y∈R tùy ý là một nghiệm của phương trình 3x+0y=5

    Biểu diễn hình học tất cả các nghiệm của phương trình 3x+0y=5

    Cho y=1⇒x=53⇒A(53;1)

    y=0⇒x=53⇒B(53;0)

    Đường thẳng 3x+0y=5 đi qua hai điểm A và B

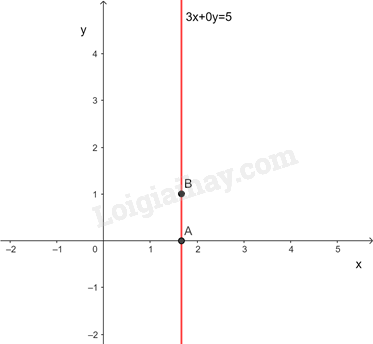
    Toán 9 Bài 1 (Kết nối tri thức): Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn (ảnh 1)

    Bài 1.4 trang 10 Toán 9 Tập 1:

    a) Hệ phương trình {2x=−65x+4y=1 có là một hệ hai phương trình bậc nhất hai ẩn không, vì sao?

    b) Cặp số (−3;4) có là một nghiệm của hệ phương trình đó hay không, vì sao?

    Lời giải:

    a) Hệ phương trình đã cho là hệ phương trình bậc nhất hai ẩn vì 2x=−6 và 5x+4y=1 là hai phương trình bậc nhất 2 ẩn thỏa mãn điều kiện a≠0 hoặc b≠0.

    b) Thay (−3;4) vào hệ phương trình ta có {2.(−3)=−65.(−3)+4.4=1 (luôn đúng)

    Vậy (−3;4) là nghiệm của hệ phương trình.

    Bài 1.5 trang 10 Toán 9 Tập 1:

    Cho các cặp số (−2;1),(0;2),(1;0),(1,5;3),(4;−3) và hai phương trình

    5x+4y=8,(1)3x+5y=−3.(2)

    Trong các cặp số đã cho:

    a) Những cặp số nào là nghiệm của phương trình (1)?

    b) Cặp số nào là nghiệm của hệ hai phương trình gồm (1) và (2)?

    c) Vẽ hai đường thẳng 5x+4y=8 và 3x+5y=−3 trên cùng một mặt phẳng tọa độ để minh họa kết luận ở câu b.

    Lời giải:

    a) Thay (−2;1) vào phương trình (1) ta có: 5.(−2)+4.1=8 (vô lí)

    Thay (0;2) vào phương trình (1) ta có: 5.0+4.2=8 (luôn đúng)

    Thay (1;0) vào phương trình (1) ta có: 5.1.+4.0=8 (vô lí)

    Thay (1,5;3) vào phương trình (1) ta có: 5.1,5+4.0=8 (vô lí)

    Thay (4;−3) vào phương trình (1) ta có: 5.4+4.(−3)=8 (luôn đúng)

    Vậy nghiệm của phương trình (1) là (0;2) và (4;−3).

    b) Vì (−2;1), (1;0) và (1,5;3) không là nghiệm của phương trình (1) nên cũng không là nghiệm của hệ phương trình gồm (1) và (2).

    Thay (0;2) vào phương trình (2) ta có: 3.0+5.2=−3 (vô lí).

    Thay (4;−3) vào phương trình (2) ta có: 3.4+5.(−3)=−3 (luôn đúng).

    Vậy (4;−3) là nghiệm của hệ phương trình gồm (1) và (2).

    c) Đường thẳng 5x+4y=8

    Cho x=0⇒y=2⇒A(0;2)

    y=0⇒x=85⇒B(85;0)

    Đường thẳng 5x+4y=8 đi qua điểm A và B

    Đường thẳng 3x+5y=−3

    Cho x=0⇒y=−35⇒C(0;−35)

    y=0⇒x=−1⇒D(−1;0)

    Đường thẳng 3x+5y=−3 đi qua điểm C và D

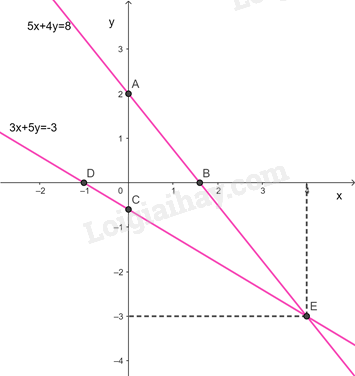
    Toán 9 Bài 1 (Kết nối tri thức): Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn (ảnh 1)

    Ta có điểm E(4;−3) là giao điểm của đường thẳng 5x+4y=8 và đường thẳng 3x+5y=−3 nên (4;−3) là nghiệm của hệ phương trình gồm (1) và (2)

    Xem thêm lời giải bài tập Toán lớp 9 Kết nối tri thức hay, chi tiết khác:

    Bài 2: Giải hệ hai phương trình bậc nhất hai ẩn

    Luyện tập chung trang 19

    Bài 3: Giải bài toán bằng cách lập hệ phương trình

    Bài tập cuối chương 1 trang 24

    Bài 4: Phương trình quy về phương trình bậc nhất một ẩn

    Tham khảo các loạt bài Toán 9 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 2,953 20/04/2024
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: