Giải Toán 9 (Kết nối tri thức): Luyện tập chung (trang 91)

Giải bài tập Toán 9 Luyện tập chung (trang 91)

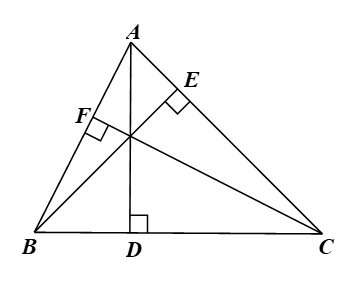
Bài 9.31 trang 91 Toán 9 Tập 2: Cho tam giác ABC có các đường cao AD, BE, CF. Chứng minh rằng BCEF, CAFD, ABDE là những tứ giác nội tiếp.

Lời giải:

⦁ Vì ∆BEC vuông tại E (do BE ⊥ AC) nên tam giác có đường tròn ngoại tiếp đường tròn đường kính BC. Do đó ba điểm B, E, C cùng nằm trên đường tròn đường kính BC.

Vì ∆BFC vuông tại F (do CF ⊥ AB) nên tam giác có đường tròn ngoại tiếp là đường tròn đường kính BC. Do đó ba điểm B, F, C cùng nằm trên đường tròn đường kính BC.

Suy ra bốn điểm B, C, E, F cùng nằm trên một đường tròn hay tứ giác BCEF là tứ giác nội tiếp.

⦁ Chứng minh tương tự, ta cũng có tứ giác CAFD nội tiếp đường tròn đường kính AC và tứ giác ABDE nội tiếp đường tròn đường kính AB.

Vậy BCEF, CAFD, ABDE là những tứ giác nội tiếp.

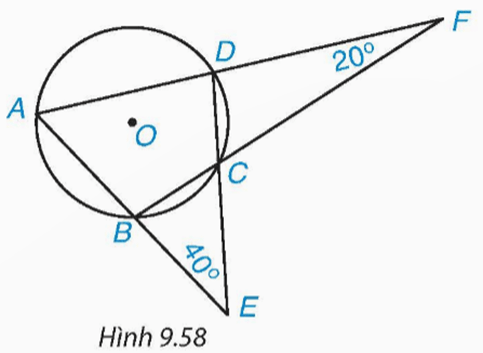
Bài 9.32 trang 91 Toán 9 Tập 2: Cho tứ giác ABCD nội tiếp đường tròn (O), AB cắt CD tại E, AD cắt BC tại F như Hình 9.58. Biết $\widehat{BEC}=40°$ và $\widehat{DFC}=20°,$ tính số đo các góc của tứ giác ABCD.

Lời giải:

Xét ∆ABF có $\hat{A}+\widehat{ABF}+\hat{F}=180°$ (tổng ba góc của tam giác)

Do đó $\widehat{ABF}=180°-\hat{F}-\hat{A}=180°-20°-\hat{A}=160°-\hat{A}.$

Xét ∆ADE có $\hat{A}+\widehat{ADE}+\hat{E}=180°$ (tổng ba góc của tam giác)

Do đó $\widehat{ADE}=180°-\hat{E}-\hat{A}=180°-40°-\hat{A}=140°-\hat{A}.$

Vì ABCD là tứ giác nội tiếp đường tròn (O) nên tổng các góc đối nhau của tứ giác bằng 180°, do đó $\hat{A}+\widehat{BCD}=180°,$ suy ra $\widehat{BCD}=180°-\hat{A}.$

Xét tứ giác ABCD có:

$\hat{A}+\widehat{ABC}+\widehat{BCD}+\widehat{ADC}=360°$ (tổng các góc của một tứ giác)

Suy ra $\hat{A}+\left(160°-\hat{A}\right)+\left(180°-\hat{A}\right)+\left(140°-\hat{A}\right)=360°$

Hay $2\hat{A}=120°,$ nên $\hat{A}=60°.$

Do đó $\widehat{ABC}=160°-\hat{A}=160°-60°=100°;$

$\widehat{ADC}=140°-\hat{A}=140°-60°=80°;$

$\widehat{BCD}=180°-\hat{A}=180°-60°=120°.$

Vậy tứ giác ABCD có $\hat{A}=60°;\widehat{ABC}=100°;\widehat{BCD}=120°;\widehat{ADC}=80°.$

Bài 9.33 trang 91 Toán 9 Tập 2: Cho hình vuông ABCD có cạnh bằng 4 cm. Tính chu vi, diện tích của các đường tròn nội tiếp và ngoại tiếp hình vuông ABCD.

Lời giải:

Gọi R là bán kính đường tròn ngoại tiếp hình vuông ABCD.

Khi đó ta có R = $\frac{1}{2}$AC.

Xét ∆ABC vuông tại B (do ABCD là hình vuông), theo định lí Pythagore, ta có:

AC² = AB² + BC² = 4² + 4² = 32.

Do đó AC = $\sqrt{32}=4\sqrt{2}$ (cm).

Suy ra $R=\frac{1}{2}AC=\frac{1}{2}\cdot 4\sqrt{2}=2\sqrt{2}\text{(cm).}$

Chu vi của đường tròn ngoại tiếp hình vuông ABCD là:

$2\pi R=2\pi \cdot 2\sqrt{2}=4\pi \sqrt{2}\text{(cm).}$

Diện tích của đường tròn ngoại tiếp hình vuông ABCD là:

$\pi R^2=\pi \cdot {\left(2\sqrt{2}\right)}^2=8\pi {\text{(cm}}^2\text{).}$

Gọi r là bán kính đường tròn nội tiếp hình vuông ABCD.

Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA.

Vì ABCD là hình vuông nên hai đường chéo AC, BD vuông góc với nhau tại trung điểm O của mỗi đường.

Xét ∆OAB vuông tại O có OM là đường trung tuyến ứng với cạnh huyền nên OM = $\frac{1}{2}$AB.

Mặt khác, ∆OAB cân tại O (vì OA = OB) nên đường trung tuyến OM đồng thời là đường cao, do đó OM ⊥ AB tại M.

Tương tự, ta có:

⦁ ON ⊥ BC tại N, OP ⊥ CD tại P, OQ ⊥ AD tại Q.

⦁ ON = $\frac{1}{2}$BC, OP = $\frac{1}{2}$CD, OQ = $\frac{1}{2}$DA.

Mà AB = BC = CD = DA (do ABCD là hình vuông)

Nên OM = ON = OP = OQ.

Vậy đường tròn (O; OM) là đường tròn nội tiếp hình vuông ABCD.

Khi đó ta có r = OM = $\frac{1}{2}$AB = $\frac{1}{2}$.4 = 2 (cm).

Chu vi của đường tròn nội tiếp hình vuông ABCD là:

2πr = 2π.2 = 4π (cm).

Diện tích của đường tròn nội tiếp hình vuông ABCD là:

πr² = π.2² = 4π (cm²).

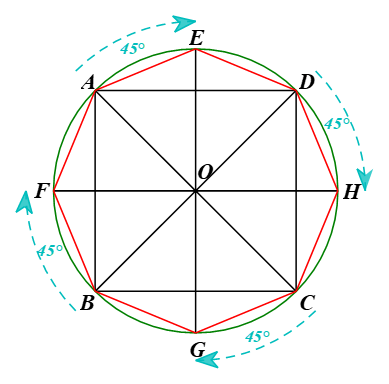
Bài 9.34 trang 91 Toán 9 Tập 2: Biết rằng bốn đỉnh A, B, C, D của một hình vuông cùng nằm trên một đường tròn (O) theo thứ tự ngược chiều quay của kim đồng hồ. Phép quay thuận chiều 45° biến các điểm A, B, C, D lần lượt thành các điểm E, F, G, H.

a) Vẽ đa giác EAFBGCHD.

b) Đa giác EAFBGCHD có phải là một bát giác đều hay không? Vì sao?

Lời giải:

a)

⦁ Vẽ đường tròn (O). Trên đường tròn (O) vẽ hình vuông ABCD sao cho các đỉnh ABCD sao cho các đỉnh A, B, C, D theo thứ tự ngược chiều kim đồng hồ.

⦁ Lấy điểm E thuộc đường tròn (O) sao cho tia OA quay thuận chiều kim đồng hồ đến tia OE và $\widehat{AOE}=45°.$

⦁ Xác định các điểm F, G, H tương tự như cách xác định điểm E ở trên. Nối A với E, E với D, D với H, H với C, C với G, G với B, B với F và F với A. Khi đó ta được đa giác EAFBGCHD.

b) Vì ABCD là hình vuông nên đường tròn (O) ngoại tiếp hình vuông có tâm O là giao điểm hai đường chéo. Do đó AC ⊥ BD tại O hay $\widehat{AOD}=90°.$

Suy ra $\widehat{AOE}+\widehat{EOD}=90°,$ suy ra $\widehat{AOE}=90°-\widehat{EOD}=90°-45°=45°.$

Xét ∆OAE và ∆OED có:

OA = OE, $\widehat{AOE}=\widehat{EOD}$ (cùng bằng 45°), OE = OD.

Do đó ∆OAE = ∆OED (c.g.c).

Tương tự, ta sẽ chứng minh được:

∆OAE = ∆OED = ∆ODH = ∆OHC = ∆OCG = ∆OGB = ∆OBF = ∆OFA.

Suy ra:

⦁ AE = ED = DH = HC = CG = GB = BF = FA; (1)

⦁ $\widehat{OAE}=\widehat{OED}=\widehat{ODH}=\widehat{OHC}=\widehat{OCG}=\widehat{OGB}=\widehat{OBF}=\widehat{OFA};$

⦁ $\widehat{OEA}=\widehat{ODE}=\widehat{OHD}=\widehat{OCH}=\widehat{OGC}=\widehat{OBG}=\widehat{OFB}=\widehat{OAF}.$

Xét ∆OAE có OA = OE nên ∆OAE cân tại O, suy ra $\widehat{OAE}=\widehat{OEA}.$

Suy ra $\widehat{OAE}+\widehat{OAF}=\widehat{OED}+\widehat{OEA}=\widehat{ODH}+\widehat{ODE}=\widehat{OHC}+\widehat{OHD}$

$=\widehat{OCG}+\widehat{OCH}=\widehat{OGB}+\widehat{OGC}=\widehat{OBF}+\widehat{OBG}=\widehat{OFA}+\widehat{OFB}.$

Hay $\widehat{EAF}=\widehat{AFB}=\widehat{FBG}=\widehat{BGC}=\widehat{GCH}=\widehat{CHD}=\widehat{HDE}=\widehat{DEA}.\left(2\right)$

Từ (1) và (2) suy ra EAFBGCHD có các cạnh bằng nhau và các góc bằng nhau.

Vậy EAFBGCHD là bát giác đều.

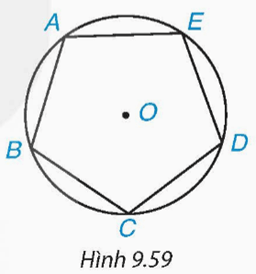
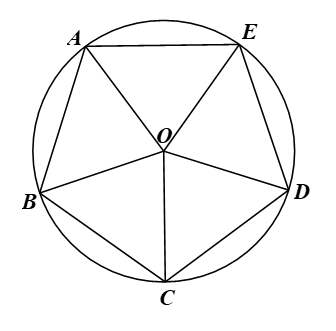
Bài 9.35 trang 91 Toán 9 Tập 2: Cho ngũ giác đều ABCDE nội tiếp đường tròn (O) như Hình 9.59.

a) Hãy tìm một phép quay thuận chiều tâm O biến điểm A thành điểm C.

b) Phép quay trên sẽ biến các điểm B, C, D, E lần lượt thành những điểm nào? Phép quay này có giữ nguyên ngũ giác đều ABCDE không?

Lời giải:

a)

Vì ngũ giác ABCDE nội tiếp đường tròn (O) nên OA = OB = OC = OD = OE.

Vì ABCDE là ngũ giác đều nên AB = BC = CD = DE = EA.

Xét ∆OAB và ∆OBC có:

OA = OB, OB = OC, AB = BC.

Do đó ∆OAB = ∆OBC (c.c.c).

Chứng minh tương tự ta có

∆OAB = ∆OBC = ∆COD = ∆DOE = ∆EOA.

Suy ra $\widehat{AOB}=\widehat{BOC}=\widehat{COD}=\widehat{DOE}=\widehat{EOA}.$

Mà $\widehat{AOB}+\widehat{BOC}+\widehat{COD}+\widehat{DOE}+\widehat{EOA}=360°$

Do đó $5\widehat{AOB}=360°$

Suy ra $\widehat{AOB}=\widehat{BOC}=\widehat{COD}=\widehat{DOE}=\widehat{EOA}=\frac{360°}{5}=72°.$

Khi đó số đo của cung lớn AC bằng:

$\widehat{AOE}+\widehat{EOD}+\widehat{DOC}=72°+72°+72°=216°.$

Do đó, để biến điểm A thành điểm C thì tia OA phải quay thuận chiều kim đồng hồ đến tia OC, điểm A tạo nên cung AC có số đo 216°.

Vậy phép quay thuận chiều 216° tâm O biến điểm A thành điểm C.

b) Phép quay thuận chiều 216° tâm O biến các điểm B, C, D, E lần lượt thành những điểm D, E, A, B.

Khi đó phép quay này giữ nguyên ngũ giác đều ABCDE.

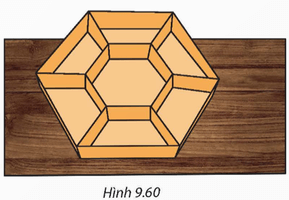
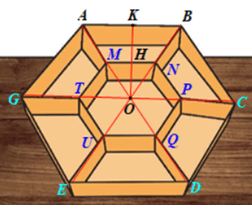
Bài 9.36 trang 91 Toán 9 Tập 2: Người ta muốn làm một khay đựng bánh kẹo hình lục giác đều có cạnh 10 cm và chia thành 7 ngăn gồm một lục giác đều nhỏ và 6 hình thang cân như Hình 9.60. Hỏi lục giác đều nhỏ phải có cạnh bằng bao nhiêu để nó có diện tích bằng hai lần diện tích mỗi hình thang?

Lời giải:

Giả sử ABCDEG là khay bánh kẹo hình lục giác đều cạnh 10 cm, được chia thành 7 ngăn gồm một lúc giác đều nhỏ MNPQUT và 6 hình thang cân MNBA, NPCB, PQDC, QUED, UTGE, TMAG.

Gọi O là giao điểm của ba đường chéo chính AD, BE, CG của hình lục giác đều ABCDEG.

Hình lục giác đều MNPQUT chia thành 6 tam giác đều OMN, ONP, OPQ, OPU, OUT, OTM.

Ta dễ dàng chứng minh được các tam giác đều đó bằng nhau nên chúng có diện tích bằng nhau.

Khi đó, S_MNPQUT = 6S_OMN.

Kẻ OK ⊥ AB, ta có K là trung điểm của AB nên AK = 5 cm.

Ta có MN // AB (do MNBA là hình thang cân) nên OK ⊥ MN.

Gọi H là giao điểm của OK và AB, ta có OH ⊥ MN và H là trung điểm của MN.

Gọi x (cm, 0 < x < 10) là độ dài cạnh của lục giác đều MNPQUT, ta có MN = x, MH = $\frac{x}{2}$.

Vì ABCDEG là lục giác đều nên ∆OAB là tam giác đều, do đó $\widehat{OAB}=60°.$

Xét ∆OAK vuông tại K, ta có:

OK = AKtan$\widehat{OAK}$ = 5.tan60^o = 5$\sqrt{3}$ (cm).

Xét ∆OMH vuông tại H, ta có:

OH = MH = tan$\widehat{OMH}$ = $\frac{x}{2}$.tan60^o = $\frac{x\sqrt{3}}{2}$ (cm).

Suy ra HK = OK = OH = 5$\sqrt{3}$ - $\frac{x\sqrt{3}}{2}$ = $\frac{\left(10-x\right)\sqrt{3}}{2}$ (cm).

Diện tích của tam giác OMN là:

$S_1=\frac{1}{2}\cdot OH\cdot MN=\frac{1}{2}\cdot \frac{x\sqrt{3}}{2}\cdot x=\frac{x^2\sqrt{3}}{4}{\text{(cm}}^2\text{).}$

Diện tích của hình thang cân MNBA là:

$S_2=\frac{1}{2}\cdot HK\cdot \left(MN+AB\right)=\frac{1}{2}\cdot \frac{\left(10-x\right)\sqrt{3}}{2}\cdot \left(x+10\right)\text{=}\frac{\left(100-x^2\right)\sqrt{3}}{4}{\text{(cm}}^2\text{).}$

Để diện tích lục giác đều MNPQNT bằng hai lần diện tích mỗi hình thang (chẳng hạn hình thang MNBA) thì: 6S₁ = 2S₂ hay 3S₁ = S₂.

Do đó $3\cdot \frac{x^2\sqrt{3}}{4}=\frac{\left(100-x^2\right)\sqrt{3}}{4}$

Suy ra 3x² = 100 – x²

4x² = 100

x² = 25

x = 5 (do x > 5).

Vậy cạnh hình lục giác đều nhỏ bằng 5 cm.

Xem thêm Lời giải bài tập Toán 9 Kết nối tri thức hay, chi tiết khác:

Bài tập cuối chương 9

Bài 31: Hình trụ và hình nón

Bài 32: Hình cầu

Luyện tập chung

Bài tập cuối chương 10