Giải Toán 9 (Kết nối tri thức): Luyện tập chung (trang 19)

Giải bài tập Toán 9 Luyện tập chung (trang 19)

Bài 6.16 trang 19 Toán 9 Tập 2: Biết rằng parabol y = ax² (a ≠ 0) đi qua điểm $A\left(2;4\sqrt{3}\right).$

a) Tìm hệ số a và vẽ đồ thị của hàm số y = ax² với a vừa tìm được.

b) Tìm tung độ của điểm thuộc parabol có hoành độ x = –1.

c) Tìm các điểm thuộc parabol có tung độ y = 5$\sqrt{3}$.

Lời giải:

a) ⦁ Do parabol y = ax² (a ≠ 0) đi qua điểm $A\left(2;4\sqrt{3}\right)$ nên ta thay x = 2 và y = 4$\sqrt{3}$ vào y = ax², ta được:

4$\sqrt{3}$ = a.2², hay 4a = 4$\sqrt{3}$ nên suy ra a = $\sqrt{3}$ (thỏa mãn a ≠ 0).

Khi đó, ta có parabol $y=\sqrt{3}{x}^2.$

⦁ Vẽ parabol $y=\sqrt{3}{x}^2.$

Bảng giá trị:

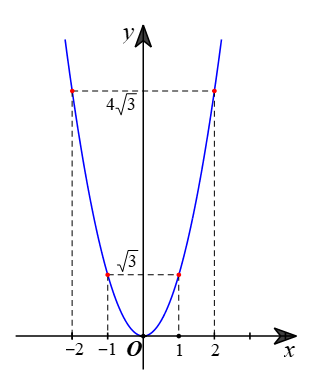
Biểu diễn các điểm $\left(-2;4\sqrt{3}\right),$$\left(-1;\sqrt{3}\right),$ $\left(0;0\right),$ $\left(1;\sqrt{3}\right),$$\left(2;4\sqrt{3}\right)$ trên mặt phẳng tọa độ Oxy và nối chúng lại ta được parabol $y=\sqrt{3}{x}^2$ như hình dưới đây:

b) Thay x = –1 vào $y=\sqrt{3}{x}^2,$ ta được $y=\sqrt{3}\cdot {\left(-1\right)}^2=\sqrt{3}.$

Vậy tung độ của điểm thuộc parabol có hoành độ x = –1 là y = $\sqrt{3}$

c) Thay y = 5$\sqrt{3}$ vào $y=\sqrt{3}{x}^2,$ ta được:

$\sqrt{3}{x}^2=5\sqrt{3}$ hay x² = 5, suy ra x = $\sqrt{5}$ hoặc x = -$\sqrt{5}$

Vậy có hai điểm cần tìm là $\left(\sqrt{5};5\sqrt{3}\right)$ và $\left(-\sqrt{5};5\sqrt{3}\right).$

Bài 6.17 trang 20 Toán 9 Tập 2: Công thức $E=\frac{1}{2}m{v}^2\left(J\right)$ được dùng để tính động năng của một vật có khối lượng m (kg) khi chuyển động với vận tốc v (m/s) (theo Vật lí đại cương, NXB Giáo dục Việt Nam, 2016).

a) Giả sử một quả bóng có khối lượng 2 kg đang bay với vận tốc 6 m/s. Tính động năng của quả bóng đó.

b) Giả sử động năng của quả bóng đang bay có khối lượng 1,5 kg là 48 J, hãy tính vận tốc bay của quả bóng đó.

Lời giải:

a) Vì quả bóng có khối lượng 2 kg đang bay với vận tốc 6 m/s nên m = 2 (kg) và v = 6 (m/s).

Thay m = 2, v = 6 vào $E=\frac{1}{2}m{v}^2,$ ta được:

$E=\frac{1}{2}\cdot 2\cdot 6^2=36\left(J\right).$

Vậy động năng của quả bóng đó là 36 (J).

b) Vì động năng của quả bóng đang bay có khối lượng 1,5 kg là 48 J nên m = 1,5 (kg), E = 48 (J).

Thay m = 1,5 và E = 48 vào $E=\frac{1}{2}m{v}^2,$ ta được:

$48=\frac{1}{2}\cdot 1,5\cdot v^2$ hay v² = 64. Suy ra v = 8 (m/s) do v > 0.

Vậy vận tốc bay của quả bóng là 8 m/s.

Bài 6.18 trang 20 Toán 9 Tập 2: Cho hình chóp tam giác đều có đáy là tam giác đều cạnh a (cm) và chiều cao 10 cm.

a) Tính diện tích đáy S của hình chóp theo a.

b) Từ kết quả ở câu a, tính thể tích V của hình chóp theo a và tính giá trị của V khi a = 4 cm.

c) Nếu độ dài cạnh đáy giảm đi hai lần thì thể tích hình chóp thay đổi thế nào?

Lời giải:

a) Xét ∆ABC đều cạnh a, kẻ AH ⊥ BC.

Do ∆ABC đều nên đường cao AH đồng thời là đường trung tuyến của tam giác, nên H là trung điểm của BC. Suy ra BH = $\frac{1}{2}$BC = $\frac{a}{2}$ (cm).

Xét ∆ABH vuông tại H, theo định lí Pythagore, ta có:

AB² = AH² + BH²

Suy ra $A{H}^2=A{B}^2-B{H}^2=a^2-{\left(\frac{a}{2}\right)}^2=\frac{3a^2}{4}.$

Do đó $AH=\frac{a\sqrt{3}}{2}\text{(cm).}$

Khi đó, diện tích của tam giác ABC là:

$S=\frac{1}{2}AH\cdot BC=\frac{1}{2}\cdot \frac{a\sqrt{3}}{2}\cdot a=\frac{a^2\sqrt{3}}{4}{\text{(cm}}^2\text{).}$

Vậy diện tích đáy của hình chóp tam giác đều cạnh a là $S=\frac{a^2\sqrt{3}}{4}{\text{(cm}}^2\text{).}$

b) Thể tích của hình chóp là:

$V=\frac{1}{3}Sh=\frac{1}{3}\cdot \frac{a^2\sqrt{3}}{4}\cdot 10=\frac{5a^2\sqrt{3}}{6}{\text{ (cm}}^3\text{).}$

Khi a = 4, thay vào $V=\frac{5a^2\sqrt{3}}{6},$ ta được:

$V=\frac{5\cdot 4^2\cdot \sqrt{3}}{6}=\frac{40\sqrt{3}}{3}{\text{(cm}}^3\text{).}$

c) Nếu độ dài cạnh đáy giảm đi 2 lần thì độ dài cạnh đáy của hình chóp lúc này là $\frac{a}{2}\text{(cm).}$

Diện tích đáy của hình chóp là: $S^{\text{'}}=\frac{{\left(\frac{a}{2}\right)}^2\cdot \sqrt{3}}{4}\text{=}\frac{a^2\sqrt{3}}{16}{\text{(cm}}^2\text{).}$

Thể tích của hình chóp lúc này là:

$V^{\text{'}}=\frac{1}{3}{S}^{\text{'}}h=\frac{1}{3}\cdot \frac{a^2\sqrt{3}}{16}\cdot 10=\frac{5a^2\sqrt{3}}{24}\text{=}\frac{V}{4}{\text{(cm}}^3\text{).}$

Vậy độ dài cạnh đáy giảm đi hai lần thì thể tích hình chóp giảm đi 6 lần.

Bài 6.19 trang 20 Toán 9 Tập 2: Sử dụng công thức nghiệm hoặc công thức nghiệm thu gọn, giải các phương trình sau:

a) $x^2-2\sqrt{5}x+1=0;$

b) 3x² – 9x + 3 = 0;

c) 11x² – 13x + 5 = 0;

d) $2x^2+2\sqrt{6}x+3=0.$

Lời giải:

a) $x^2-2\sqrt{5}x+1=0$

Ta có a = 1, $b^{\text{'}}=-\sqrt{5},$ c = 1 và ${\Delta }^{\text{'}}={\left(-\sqrt{5}\right)}^2-1\cdot 1=4>0,$ $\sqrt{{\Delta }^{\text{'}}}=\sqrt{4}=2.$

Do đó, phương trình có hai nghiệm phân biệt:

$x_1=\frac{-\left(-\sqrt{5}\right)+2}{1}=\sqrt{5}+2;x_2=\frac{-\left(-\sqrt{5}\right)-2}{1}=\sqrt{5}-2.$

b) 3x² – 9x + 3 = 0

Ta có a = 3, b = –9, c = 3 và ∆ = (–9)² – 4.3.3 = 45 > 0, $\sqrt{\Delta }=\sqrt{45}=3\sqrt{5}.$

Do đó, phương trình có hai nghiệm phân biệt:

$x_1=\frac{-\left(-9\right)+\sqrt{45}}{2\cdot 3}=\frac{3+\sqrt{5}}{2};x_2=\frac{-\left(-9\right)-\sqrt{45}}{2\cdot 3}=\frac{3-\sqrt{5}}{2}.$

c) 11x² – 13x + 5 = 0

Ta có a = 11, b = –13, c = 5 và ∆ = (–13)² – 4.11.5 = –51 < 0.

Do đó, phương trình vô nghiệm.

d) $2x^2+2\sqrt{6}x+3=0.$

Ta có a = 2, $b^{\text{'}}=\sqrt{6},$ c = 3 và ${\Delta }^{\text{'}}={\left(\sqrt{6}\right)}^2-2\cdot 3=0.$

Do đó, phương trình có nghiệm kép $x_1=x_2=-\frac{\sqrt{6}}{2}.$

Bài 6.20 trang 20 Toán 9 Tập 2: Sử dụng máy tính cầm tay, tìm nghiệm gần đúng của các phương trình sau (làm tròn kết quả đến chữ số thập phân thứ hai):

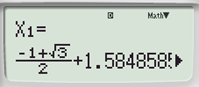
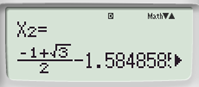
a) $\sqrt{2}{x}^2-\sqrt{5}x+1=0;$

b) $x^2-\left(\sqrt{3}-1\right)x+\sqrt{7}=0.$

Lời giải:

Với mỗi loại máy tính cầm tay, sau khi mở máy ta bấm phím để chuyển về chế độ giải phương trình bậc hai.

Tiếp theo, với từng phương trình ta thực hiện như sau:

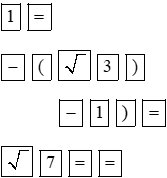
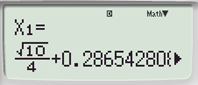
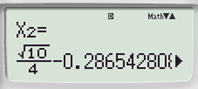
Tìm nghiệm của phương trình	Bấm phím	Màn hình hiện	Kết luận
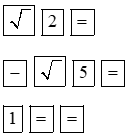$\sqrt{2}{x}^2-\sqrt{5}x+1=0$		Bấm tiếp phím	Phương trình vô nghiệm.
$x^2-\left(\sqrt{3}-1\right)x+\sqrt{7}=0$		Bấm tiếp phím	Phương trình vô nghiệm.

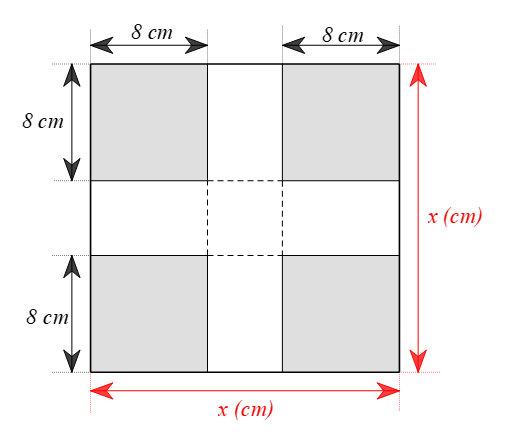
Bài 6.21 trang 20 Toán 9 Tập 2: Từ một tấm tôn hình vuông, người ta cắt bỏ bốn hình vuông có độ dài cạnh 8 cm ở bốn góc, sau đó gập thành một chiếc thùng có dạng hình hộp chữ nhật không có nắp và có thể tích là 200 cm³. Tính độ dài cạnh của tấm tôn hình vuông ban đầu.

Lời giải:

Gọi độ dài cạnh của tấm tôn ban đầu là x (cm) (x > 16).

Sau khi người ta cắt bỏ bốn hình vuông có độ dài cạnh 8 cm ở bốn góc, sau đó gập thành một chiếc thùng có dạng hình hộp chữ nhật thì:

⦁ cạnh đáy (đáy hình vuông) là: x – 8.2 = x – 16 (cm);

⦁ chiều cao là: 8 (cm).

Thể tích hình hộp chữ nhật: 8(x – 16)² (cm³).

Theo đề bài ta có phương trình: 8(x – 16)² = 200.

Giải phương trình:

8(x – 16)² = 200

(x – 16)² = 25

x – 16 = 5 hoặc x – 16 = –5

x = 21 hoặc x = 11.

Ta thấy chỉ có giá trị x = 21 thỏa mãn điều kiện x > 16.

Vậy độ dài cạnh của tấm tôn ban đầu là 21 cm.

Bài 6.22 trang 20 Toán 9 Tập 2: Giả sử doanh thu (nghìn đồng) của một cửa hàng bán phở trong một ngày có thể mô hình hoá bằng công thức R(x) = x(220 – 4x) với 30 ≤ x ≤ 50, trong đó x (nghìn đồng) là giá tiền của một bát phở. Nếu muốn doanh thu của cửa hàng đạt 3 triệu đồng thì giá bán của mỗi bát phở phải là bao nhiêu?

Lời giải:

Ta có 3 triệu đồng = 3 000 nghìn đồng.

Vì doanh thu của cửa hàng đạt 3 triệu đồng nên R(x) = 3 000.

Thay R(x) = 3 000 vào R(x) = x(220 – 4x), ta được:

3 000 = x(220 – 4x)

3 000 = 220x – 4x²

4x² – 220x + 3 000 = 0

x² – 55x + 750 = 0.

Ta có ∆ = (–55)² – 4.1.750 = 25 > 0 và $\sqrt{\Delta }=\sqrt{25}=5.$

Phương trình trên có hai nghiệm phân biệt là:

$x_1=\frac{55+5}{2\cdot 1}=30,$ $x_2=\frac{55-5}{2\cdot 1}=25.$

Vì 30 ≤ x ≤ 50 nên ta chọn x = 30 (nghìn đồng).

Vậy nếu muốn doanh thu của cửa hàng đạt 3 triệu đồng thì giá bán của mỗi bát phở là 30 nghìn đồng.

Xem thêm Lời giải bài tập Toán 9 Kết nối tri thức hay, chi tiết khác:

Bài 20: Định lí Viète và ứng dụng

Bài 21: Giải bài toán bằng cách lập phương trình

Luyện tập chung (trang 29)

Bài tập cuối chương 6

Bài 22: Bảng tần số và biểu đồ tần số