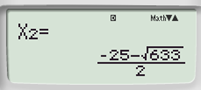Giải Toán 9 Bài 19 (Kết nối tri thức): Phương trình bậc hai một ẩn

Giải bài tập Toán 9 Bài 19: Phương trình bậc hai một ẩn

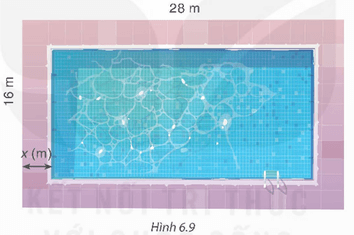
Mở đầu trang 10 Toán 9 Tập 2: Trên một mảnh đất hình chữ nhật có kích thước 28 m × 16 m, người ta dự định làm một bể bơi có đường đi xung quanh (H.6.9). Hỏi bề rộng của đường đi là bao nhiêu để diện tích của bể bơi là 288 m²?

Lời giải:

Sau bài học này, chúng ta sẽ giải được bài toán trên như sau:

Theo bài, ta có điều kiện của x là 0 < x < 8.

Chiều dài của bể bơi là: 28 – x – x = 28 – 2x (m).

Chiều rộng của bể bơi là: 16 – x – x = 16 – 2x (m).

Diện tích của bể bơi theo x là:

S = (28 – 2x)(16 – 2x) = 448 – 56x – 32x + 4x² = 4x² – 88x + 448 (m²).

Theo bài, S = 288 m² nên ta có phương trình: 4x² – 88x + 448 = 288.

Giải phương trình:

4x² – 88x + 448 = 288

4x² – 88x + 160 = 0

x² – 22x + 40 = 0.

Phương trình trên có a = 1; b’ = –11; c = 40 và ∆’ = (–11)² – 1.40 = 81 nên $\sqrt{{\Delta }^{\text{'}}}=\sqrt{81}=9.$

Do đó, phương trình trên có hai nghiệm phân biệt $x=\frac{11+9}{1}=20$ và $x=\frac{11-9}{1}=2.$

Ta thấy chỉ có x = 2 thỏa mãn điều kiện 0 < x < 16.

Vậy bề rộng của đường đi là 2 mét để diện tích của bể bơi là 288 m².

HĐ1 trang 10 Toán 9 Tập 2: Xét bài toán trong tình huống mở đầu.

Gọi x (m) là bề rộng của mặt đường (0 < x < 8). Tính chiều dài và chiều rộng của bể bơi theo x.

Lời giải:

Chiều dài của bể bơi là: 28 – x – x = 28 – 2x (m).

Chiều rộng của bể bơi là: 16 – x – x = 16 – 2x (m).

HĐ2 trang 10 Toán 9 Tập 2: Dựa vào kết quả HĐ1, tính diện tích của bể bơi theo x.

Lời giải:

Diện tích của bể bơi theo x là:

S = (28 – 2x)(16 – 2x) = 448 – 56x – 32x + 4x² = 4x² – 88x + 448 (m²).

HĐ3 trang 10 Toán 9 Tập 2: Sử dụng giả thiết và kết quả HĐ2, hãy viết phương trình để tìm x.

Lời giải:

Theo bài, diện tích của bể bơi là S = 288 m² nên ta có phương trình:

4x² – 88x + 448 = 288

4x² – 88x + 160 = 0.

Luyện tập 1 trang 11 Toán 9 Tập 2: Trong các phương trình sau, những phương trình nào là phương trình bậc hai ẩn x? Chỉ rõ các hệ số a, b, c của mỗi phương trình đó.

a) x² + 5 = 0;

b) 2x² + 7x = 0;

c) $\frac{x^2-2x+5}{x}=0;$

d) 0,5x² = 0.

Lời giải:

a) Phương trình x² + 5 = 0 là phương trình bậc hai ẩn x với a = 1, b = 0 và c = 5.

b) Phương trình 2x² + 7x = 0 là phương trình bậc hai ẩn x với a = 2, b = 7 và c = 0.

c) Phương trình $\frac{x^2-2x+5}{x}=0$ không phải là phương trình bậc hai.

d) Phương trình 0,5x² = 0 là phương trình bậc hai ẩn x với a = 0,5, b = c = 0.

Tranh luận trang 11 Toán 9 Tập 2: Anh Pi nói rằng: “Phương trình (ẩn x) mx² + 2x + 1 = 0 (m là một số cho trước) là một phương trình bậc hai với a = m, b = 2, c = 1”.

Ý kiến của em thế nào?

Lời giải:

Ta có:

⦁ Nếu m = 0, ta có phương trình 2x + 1 = 0, đây không phải là phương trình bậc hai.

⦁ Nếu m ≠ 0, phương trình (ẩn x) mx² + 2x + 1 = 0 là một phương trình bậc hai với a = m, b = 2, c = 1.

Vậy phương trình (ẩn x) mx² + 2x + 1 = 0 (m là một số cho trước khác 0) là một phương trình bậc hai với a = m, b = 2, c = 1.

Luyện tập 2 trang 12 Toán 9 Tập 2: Giải các phương trình sau:

a) 2x² + 6x = 0;

b) 5x² + 11x = 0.

Lời giải:

a) 2x² + 6x = 0

2x(x + 3) = 0

x = 0 hoặc x + 3 = 0

x = 0 hoặc x = –3.

Vậy phương trình có hai nghiệm x₁ = 0, x₂ = –3.

b) 5x² + 11x = 0

x(5x + 11) = 0

x = 0 hoặc 5x + 11 = 0

x = 0 hoặc $x=-\frac{11}{5}.$

Vậy phương trình có hai nghiệm x₁ = 0, $x_2=-\frac{11}{5}.$

Luyện tập 3 trang 12 Toán 9 Tập 2: Giải các phương trình sau:

a) x² – 25 = 0;

b) (x + 3)² = 5.

Lời giải:

a) x² – 25 = 0

x² = 25

x = 5 hoặc x = –5.

Vậy phương trình có hai nghiệm x₁ = 5, x₂ = –5.

b) (x + 3)² = 5

x + 3 = $\sqrt{5}$ hoặc x + 3 = -$\sqrt{5}$

x = -3+ $\sqrt{5}$ hoặc x = -3- $\sqrt{5}$

Vậy phương trình có hai nghiệm x₁ = -3+ $\sqrt{5}$, x₂ = -3- $\sqrt{5}$.

Luyện tập 4 trang 13 Toán 9 Tập 2: Cho phương trình x² + 6x = 1.

Hãy cộng vào cả hai vế của phương trình với cùng một số thích hợp để được một phương trình mà vế trái có thể biến đổi thành một bình phương. Từ đó, hãy giải phương trình đã cho.

Lời giải:

x² + 6x = 1

x² + 6x + 9 = 1 + 9

(x + 3)² = 10

x+3 = $\sqrt{10}$ hoặc x+3 = -$\sqrt{10}$

x = -3+$\sqrt{10}$ hoặc x = -3-$\sqrt{10}$

Vậy phương trình có hai nghiệm x₁ = -3+$\sqrt{10}$, x₂ = -3-$\sqrt{10}$

HĐ4 trang 13 Toán 9 Tập 2: Thực hiện lần lượt các bước sau để giải phương trình:

2x² – 8x + 3 = 0.

a) Chuyển hạng tử tự do sang vế phải.

b) Chia cả hai vế của phương trình cho hệ số của x².

c) Thêm vào hai vế của phương trình nhận được ở câu b với cùng một số để vế trái có thể biến đổi thành một bình phương. Từ đó tìm nghiệm x.

Lời giải:

a) 2x² – 8x + 3 = 0

2x² – 8x = –3.

b) $x^2-4x=-\frac{3}{2}.$

c) $x^2-4x+4=-\frac{3}{2}+4$

${\left(x-2\right)}^2=\frac{5}{2}$

x - 2 = $\sqrt{\frac{5}{2}}$hoặc x-2 = -$\sqrt{\frac{5}{2}}$

x = 2+$\frac{\sqrt{10}}{2}$ hoặc x = 2-$\frac{\sqrt{10}}{2}$

$x=\frac{4+\sqrt{10}}{2}$ hoặc $x=\frac{4-\sqrt{10}}{2}.$

Vậy phương trình đã cho có hai nghiệm $x_1=\frac{4+\sqrt{10}}{2};$ $x_2=\frac{4-\sqrt{10}}{2}.$

Luyện tập 5 trang 14 Toán 9 Tập 2: Áp dụng công thức nghiệm, giải các phương trình sau:

a) 2x² – 5x + 1 = 0;

b) x² + 8x + 16 = 0;

c) x² – x + 1 = 0.

Lời giải:

a) Ta có ∆ = (–5)² – 4.2.1 = 17 > 0.

Do đó, phương trình có hai nghiệm phân biệt:

$x_1=\frac{5+\sqrt{17}}{4},$ $x_2=\frac{5-\sqrt{17}}{4}.$

b) Ta có ∆ = 8² – 4.1.16 = 0.

Do đó, phương trình có nghiệm kép: $x_1=x_2=-\frac{8}{2}$= -4.

c) Ta có ∆ = (–1)² – 4.1.1 = –3 < 0.

Do đó, phương trình vô nghiệm.

HĐ4 trang 13 Toán 9 Tập 2: Thực hiện lần lượt các bước sau để giải phương trình:

2x² – 8x + 3 = 0.

a) Chuyển hạng tử tự do sang vế phải.

b) Chia cả hai vế của phương trình cho hệ số của x².

c) Thêm vào hai vế của phương trình nhận được ở câu b với cùng một số để vế trái có thể biến đổi thành một bình phương. Từ đó tìm nghiệm x.

Lời giải:

a) 2x² – 8x + 3 = 0

2x² – 8x = –3.

b) $x^2-4x=-\frac{3}{2}.$

c) $x^2-4x+4=-\frac{3}{2}+4$

${\left(x-2\right)}^2=\frac{5}{2}$

x - 2 = $\sqrt{\frac{5}{2}}$hoặc x-2 = -$\sqrt{\frac{5}{2}}$

x = 2+$\frac{\sqrt{10}}{2}$ hoặc x = 2-$\frac{\sqrt{10}}{2}$

$x=\frac{4+\sqrt{10}}{2}$ hoặc $x=\frac{4-\sqrt{10}}{2}.$

Vậy phương trình đã cho có hai nghiệm $x_1=\frac{4+\sqrt{10}}{2};$ $x_2=\frac{4-\sqrt{10}}{2}.$

Thử thách nhỏ trang 14 Toán 9 Tập 2: Anh Pi hỏi: “Có thể nói gì về nghiệm của phương trình bậc hai ax² + bx + c = 0 nếu a và c trái dấu?”

Em hãy trả lời câu hỏi của anh Pi.

Lời giải:

Xét phương trình bậc hai ax² + bx + c = 0 (a ≠ 0).

Ta có ∆ = b² – 4ac.

Do a và c trái dấu nên ac < 0, nên – 4ac > 0, suy ra b² – 4ac > 0 hay ∆ > 0.

Khi đó, phương trình bậc hai ax² + bx + c = 0 luôn có hai nghiệm phân biệt.

Vậy phương trình bậc hai ax² + bx + c = 0 luôn có hai nghiệm phân biệt nếu a và c trái dấu.

Luyện tập 6 trang 15 Toán 9 Tập 2: Xác định a, b’, c rồi dùng công thức nghiệm thu gọn giải các phương trình sau:

a) 3x² + 8x – 3 = 0;

b) $x^2+6\sqrt{2}x+2=0.$

Lời giải:

a) Ta có: a = 3, b’ = 4, c = –3 và ∆’ = 4² – 3.(–3) = 25 > 0, $\sqrt{{\Delta }^{\text{'}}}=\sqrt{25}=5.$

Do đó, phương trình có hai nghiệm phân biệt:

$x_1=\frac{-4+5}{3}=\frac{1}{3},$ $x_2=\frac{-4-5}{3}=\frac{-9}{3}=-3.$

b) Ta có a = 1, b = 3$\sqrt{2}$, c = 2 và ${\Delta }^{\text{'}}={\left(3\sqrt{2}\right)}^2-1\cdot 2=16>0,$ $\sqrt{{\Delta }^{\text{'}}}=\sqrt{16}=4.$

Do đó, phương trình có hai nghiệm phân biệt:

$x_1=\frac{-3\sqrt{2}+4}{1}=4-3\sqrt{2},$ $x_2=\frac{-3\sqrt{2}-4}{1}=-4-3\sqrt{2}.$

Vận dụng trang 15 Toán 9 Tập 2: Giải bài toán trong tình huống mở đầu.

Lời giải:

Theo bài, ta có điều kiện của x là 0 < x < 8.

Chiều dài của bể bơi là: 28 – x – x = 28 – 2x (m).

Chiều rộng của bể bơi là: 16 – x – x = 16 – 2x (m).

Diện tích của bể bơi theo x là:

S = (28 – 2x)(16 – 2x) = 448 – 56x – 32x + 4x² = 4x² – 88x + 448 (m²).

Theo bài, S = 288 m² nên ta có phương trình: 4x² – 88x + 448 = 288.

Giải phương trình:

4x² – 88x + 448 = 288

4x² – 88x + 160 = 0

x² – 22x + 40 = 0.

Phương trình trên có a = 1; b’ = –11; c = 40 và ∆’ = (–11)² – 1.40 = 81 nên $\sqrt{{\Delta }^{\text{'}}}=\sqrt{81}=9.$

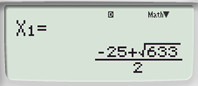
Do đó, phương trình trên có hai nghiệm phân biệt:

$x_1=\frac{11+9}{1}=20$ và $x_2=\frac{11-9}{1}=2.$

Ta thấy chỉ có x₂ = 2 thỏa mãn điều kiện 0 < x < 16.

Vậy bề rộng của đường đi là 2 mét để diện tích của bể bơi là 288 m².

Luyện tập 6 trang 15 Toán 9 Tập 2: Xác định a, b’, c rồi dùng công thức nghiệm thu gọn giải các phương trình sau:

a) 3x² + 8x – 3 = 0;

b) $x^2+6\sqrt{2}x+2=0.$

Lời giải:

a) Ta có: a = 3, b’ = 4, c = –3 và ∆’ = 4² – 3.(–3) = 25 > 0, $\sqrt{{\Delta }^{\text{'}}}=\sqrt{25}=5.$

Do đó, phương trình có hai nghiệm phân biệt:

$x_1=\frac{-4+5}{3}=\frac{1}{3},$ $x_2=\frac{-4-5}{3}=\frac{-9}{3}=-3.$

b) Ta có a = 1, b = 3$\sqrt{2}$, c = 2 và ${\Delta }^{\text{'}}={\left(3\sqrt{2}\right)}^2-1\cdot 2=16>0,$ $\sqrt{{\Delta }^{\text{'}}}=\sqrt{16}=4.$

Do đó, phương trình có hai nghiệm phân biệt:

$x_1=\frac{-3\sqrt{2}+4}{1}=4-3\sqrt{2},$ $x_2=\frac{-3\sqrt{2}-4}{1}=-4-3\sqrt{2}.$

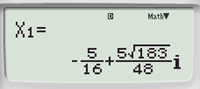
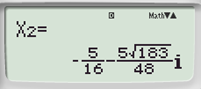
Luyện tập 7 trang 16 Toán 9 Tập 2: Sử dụng máy tính cầm tay, tìm nghiệm của các phương trình sau:

a) $5x^2+2\sqrt{10}x+2=0;$

b) 3x² – 5x + 7 = 0;

c) 4x² – 11x + 1 = 0.

Lời giải:

Với mỗi loại máy tính cầm tay, sau khi mở máy ta bấm phím để chuyển về chế độ giải phương trình bậc hai.

Tiếp theo, với từng phương trình ta thực hiện như sau:

Tìm nghiệm của phương trình	Bấm phím	Màn hình hiện	Kết luận
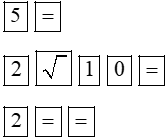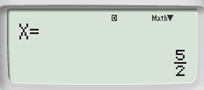
$5x^2+2\sqrt{10}x+2=0$			Phương trình có nghiệm kép: $x_1=x_2=-\frac{\sqrt{10}}{5}.$
3x2 – 5x + 7 = 0		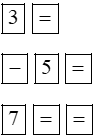Bấm tiếp phím	Phương trình vô nghiệm.
4x2 – 11x + 1 = 0		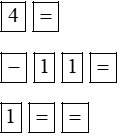Bấm tiếp phím	Phương trình có hai nghiệm phân biệt: $x_1=\frac{11+\sqrt{105}}{8};$ $x_2=\frac{11-\sqrt{105}}{8}.$

Bài 6.8 trang 16 Toán 9 Tập 2: Đưa các phương trình sau về dạng ax² + bx + x = 0 và xác định các hệ số a, b, c của phương trình đó.

a) 3x² + 2x – 1 = x² – x;

b) (2x + 1)² = x² + 1.

Lời giải:

a) 3x² + 2x – 1 = x² – x

3x² – x² + 2x + x – 1 = 0

2x² + 3x – 1 = 0

Phương trình trên có a = 2, b = 3 và c = –1.

b) (2x + 1)² = x² + 1

4x² + 4x + 1 – x² – 1 = 0

3x² + 4x = 0.

Phương trình trên có a = 3, b = 4 và c = 0.

Bài 6.9 trang 16 Toán 9 Tập 2: Giải các phương trình sau:

a) $2x^2+\frac{1}{3}x=0;$

b) (3x + 2)² = 5.

Lời giải:

a) $2x^2+\frac{1}{3}x=0$

$x\left(2x+\frac{1}{3}\right)=0$

x = 0 hoặc $2x+\frac{1}{3}=0$

x = 0 hoặc $2x=-\frac{1}{3}$

x = 0 hoặc $x=-\frac{1}{6}.$

vậy phương trình có hai nghiệm x₁ = 0, $x_2=-\frac{1}{6}.$

b) (3x + 2)² = 5.

3x + 2 = $\sqrt{5}$ hoặc 3x + 2 = -$\sqrt{5}$

3x = -2 + $\sqrt{5}$ hoặc 3x = -2-$\sqrt{5}$

$x=\frac{-2+\sqrt{5}}{3}$ hoặc $x=\frac{-2-\sqrt{5}}{3}.$

Vậy phương trình có hai nghiệm $x_1=\frac{-2+\sqrt{5}}{3},$ $x_2=\frac{-2-\sqrt{5}}{3}.$

Bài 6.10 trang 16 Toán 9 Tập 2: Không cần giải phương trình, hãy xác định các hệ số a, b, c, tính biệt thức ∆ và xác định số nghiệm của mỗi phương trình sau:

a) 11x² + 13x – 1 = 0;

b) 9x² + 42x + 49 = 0;

c) x² – 2x + 3 = 0.

Lời giải:

a) 11x² + 13x – 1 = 0

Ta có a = 11, b = 13, c = –1 và ∆ = 13² – 4.11.(–1) = 213 > 0.

Vậy phương trình trên có hai nghiệm phân biệt.

b) 9x² + 42x + 49 = 0

Ta có a = 9, b = 42, c = 49 và ∆ = 42² – 4.9.49 = 0.

Vậy phương trình trên có nghiệm kép.

c) x² – 2x + 3 = 0

Ta có a = 1, b = –2, c = 3 và ∆ = (–2)² – 4.1.3 = –8 < 0.

Vậy phương trình vô nghiệm (không có nghiệm).

Bài 6.11 trang 17 Toán 9 Tập 2: Dùng công thức nghiệm của phương trình bậc hai, giải các phương trình sau:

a) $x^2-2\sqrt{5}x+2=0;$

b) 4x² + 28x + 49 = 0;

c) $3x^2-3\sqrt{2}x+1=0.$

Lời giải:

a) $x^2-2\sqrt{5}x+2=0$

Ta có $\Delta ={\left(-2\sqrt{5}\right)}^2-4\cdot 1\cdot 2=12>0$ và $\sqrt{\Delta }=\sqrt{12}=2\sqrt{3}.$

Do đó phương trình có hai nghiệm phân biệt:

$x_1=\frac{2\sqrt{5}+2\sqrt{3}}{2}=\sqrt{5}+\sqrt{3},$ $x_2=\frac{2\sqrt{5}-2\sqrt{3}}{2}=\sqrt{5}-\sqrt{3}.$

b) 4x² + 28x + 49 = 0

Ta có $\Delta$ = 28² -4.4.49 = 0.

Do đó phương trình có nghiệm kép:

$x_1=x_2=-\frac{28}{2\cdot 4}=-\frac{7}{2}.$

c) $3x^2-3\sqrt{2}x+1=0$

Ta có $\Delta ={\left(-3\sqrt{2}\right)}^2-4\cdot 3\cdot 1=6>0.$

Do đó phương trình có hai nghiệm phân biệt:

$x_1=\frac{3\sqrt{2}+\sqrt{6}}{6},$ $x_2=\frac{3\sqrt{2}-\sqrt{6}}{6}.$

Bài 6.12 trang 17 Toán 9 Tập 2: Sử dụng máy tính cầm tay, tìm nghiệm của các phương trình sau:

a) 0,1x² + 2,5x – 0,2 = 0;

b) 0,01x² – 0,05x + 0,0625 = 0;

c) 1,2x² + 0,75x + 2,5 = 0.

Lời giải:

Với mỗi loại máy tính cầm tay, sau khi mở máy ta bấm phím để chuyển về chế độ giải phương trình bậc hai.

Tiếp theo, với từng phương trình ta thực hiện như sau:

Tìm nghiệm của phương trình	Bấm phím	Màn hình hiện	Kết luận
0,1x2 + 2,5x – 0,2 = 0		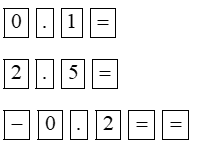Bấm tiếp phím	Phương trình có hai nghiệm phân biệt: $x_1=\frac{-25+\sqrt{633}}{2};$ $x_2=\frac{-25-\sqrt{633}}{2}.$
0,01x2 – 0,05x + 0,0625 = 0		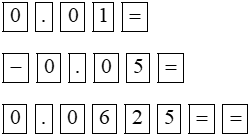	Phương trình có nghiệm kép: $x_1=x_2=\frac{5}{2}.$
1,2x2 + 0,75x + 2,5 = 0		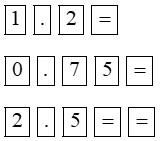Bấm tiếp phím	Phương trình vô nghiệm.

Bài 6.13 trang 17 Toán 9 Tập 2: Độ cao h (mét) so với mặt đất của một vật được phóng thẳng đứng lên trên từ mặt đất với vận tốc ban đầu v₀ = 19,6 m/s cho bởi công thức h = 19,6t – 4,9t², ở đó t là thời gian kể từ khi phóng (giây) (theo Vật lí đại cương, NXB Giáo dục Việt Nam, 2016). Hỏi sau bao lâu kể từ khi phóng, vật sẽ rơi trở lại mặt đất?

Lời giải:

Khi vật rơi trở lại mặt đất, độ cao h = 0 hay 19,6t – 4,9t² = 0 với t > 0.

Giải phương trình:

19,6t – 4,9t² = 0

t(19,6 – 4,9t) = 0

t = 0 hoặc 19,6 – 4,9t = 0

t = 0 hoặc 4,9t = 19,6

t = 0 hoặc t = 4

Ta thấy chỉ có giá trị t = 4 thỏa mãn điều kiện t > 0.

Vậy kể từ khi phóng sau 4 giây vật sẽ rơi trở lại mặt đất.

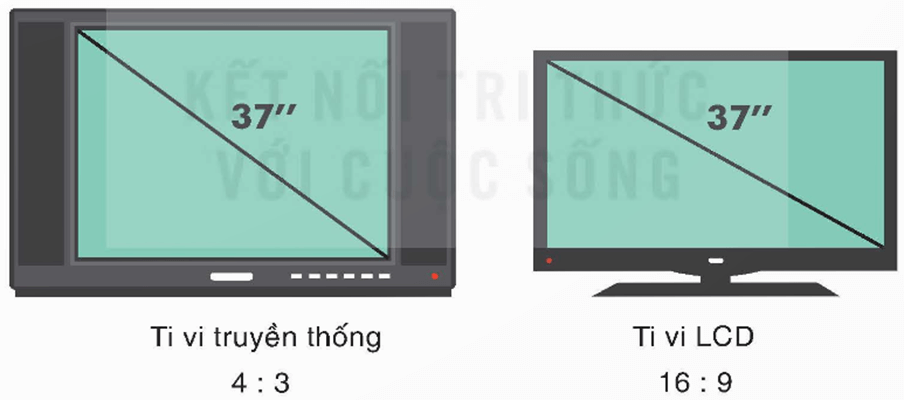
Bài 6.14 trang 17 Toán 9 Tập 2: Kích thước màn hình ti vi hình chữ nhật được xác định bằng độ dài đường chéo. Ti vi truyền thống có định dạng 4 : 3, nghĩa là tỉ lệ giữa chiều dài và chiều rộng của màn hình là 4 : 3. Hỏi diện tích của màn hình ti vi truyền thống 37 in là bao nhiêu? Diện tích của màn hình ti vi LCD 37 in có định dạng 16 : 9 là bao nhiêu? Màn hình ti vi nào có diện tích lớn hơn? Ở đây, các diện tích của màn hình được tính bằng inch vuông.

Lời giải:

Tỉ lệ giữa chiều dài và chiều rộng là 4 : 3, gọi chiều dài là 4x (in) thì chiều rộng là 3x (in) (x > 0).

Theo định lí Pythagore, ta có:

(3x)² + (4x)² = 37²

9x² + 16x² = 1 369

25x² = 1 369

x² = 54,76

x = 7,4 hoặc x = –7,4.

Ta thấy chỉ có x = 7,4 thỏa mãn điều kiện x > 0.

Diện tích của màn hình ti vi truyền thống 37 in là:

4x . 3x = 12x² = 12 . 54,76 = 657,12 (in²).

Tương tự, tỉ lệ giữa chiều dài và chiều rộng là 16 : 9, gọi chiều dài là 16y (in) thì chiều rộng là 9y (in) (y > 0).

Theo định lí Pythagore, ta có:

(9x)² + (16x)² = 37²

81x² + 256x² = 1 369

337x² = 1 369

$x^2=\frac{1369}{337}.$

Diện tích của màn hình ti vi LCD 37 in là:

$16x\cdot 9x=144x^2=144\cdot \frac{1369}{337}\approx 585$ (in²).

Ta thấy 657,12 > 585.

Do đó, màn hình ti vi truyền thống có diện tích lớn hơn.

Bài 6.15 trang 17 Toán 9 Tập 2: Một mảnh vườn hình chữ nhật có chiều rộng ngắn hơn chiều dài 6 m và có diện tích là 280 m². Tính các kích thước của mảnh vườn đó.

Lời giải:

Gọi chiều rộng mảnh vườn hình chữ nhật là x (m) (x > 0).

Chiều rộng ngắn hơn chiều dài 6 m nên chiều dài mảnh vườn là x + 6 (m).

Diện tích mảnh vườn là: x(x + 6) (m²).

Theo bài, mảnh vườn có diện tích là 280 m² nên ta có phương trình:

x(x + 6) = 280.

x² + 6x – 280 = 0.

Ta có ∆’ = 3² – 1.(–280) = 289 > 0 và $\sqrt{289}=17.$

Do đó, phương trình có hai nghiệm phân biệt:

x₁ = –3 + 17 = 14, x₂ = –3 – 17 = –20.

Ta thấy chỉ có giá trị x₁ = 14 thỏa mãn điều kiện x > 0.

Vậy chiều rộng mảnh vườn là 14 m và chiều dài mảnh vườn là 14 + 6 = 20 (m).

Xem thêm Lời giải bài tập Toán 9 Kết nối tri thức hay, chi tiết khác:

Luyện tập chung (trang 19)

Bài 20: Định lí Viète và ứng dụng

Bài 21: Giải bài toán bằng cách lập phương trình

Luyện tập chung (trang 29)

Bài tập cuối chương 6