Toán 6 Bài 13 (Cánh diều): Bội chung và bội chung nhỏ nhất
[Toán 6 - Cánh diều] Với giải bài tập Toán lớp 6 Bài 13: Bội chung và bội chung nhỏ nhất bộ sách Cánh diều chi tiết được Giáo viên nhiều năm kinh nghiệm biên soạn bám sát nội dung sách giáo khoa Toán 6 Tập 1 giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 6.
Giải Toán 6 Bài 13: Bội chung và bội chung nhỏ nhất
Trả lời câu hỏi giữa bài
Cô Ánh phải mua ít nhất bao nhiêu bộ cốc và bao nhiêu hộp bóng bàn?
Lời giải:
Sau khi học bài này, ta sẽ biết được số chiếc cốc và số quả bóng bàn mà cô Ánh phải mua ít nhất là bội chung nhỏ nhất của 6 và 8.
Ta có: 6 = 2 . 3 và 8 = 23
Các thừa số nguyên tố chung và riêng của 6 và 8 là 2 và 3
Số mũ lớn nhất của 2 là 3, số mũ lớn nhất của 3 là 1
Khi đó BCNN(6, 8) = 23 . 3 = 24
Do đó cô Ánh phải mua 24 chiếc cốc và 24 quả bóng bàn.
Số bộ cốc là: 24 : 8 = 3 (bộ)
Số hộp bóng bàn là: 24 : 6 = 4 (hộp)
Vậy cô Ánh cần mua ít nhất 3 bộ cốc và 4 hộp bóng bàn để số bóng bàn và số cốc bằng nhau.
Toán lớp 6 trang 53 Hoạt động 1:
a) Nêu một số bội của 2 và của 3 theo thứ tự tăng dần:
b) Tìm các số vừa ở trong hàng thứ nhất vừa ở trong hàng thứ hai.
c) Xác định số nhỏ nhất khác 0 trong các bội chung của 2 và 3.
Lời giải:
a)
|
Một số bội của 2 |
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
|
Một số bội của 3 |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
27 |
30 |
b) Các số vừa ở hàng thứ nhất vừa ở hàng thứ 2 là: 0, 6, 12, 18.
c) Số nhỏ nhất khác 0 trong bội chung của 2 và 3 là: 6.
Toán lớp 6 trang 54 Luyện tập 1: Hãy nêu bốn bội chung của 5 và 9.
Lời giải:
+ Trước tiên ta tìm các bội của 5 và 9.
+ Để tìm bội của 5, ta lần lượt lấy 5 nhân với các số 0; 1; 2; 3;…
Một số bội của 5 là: 0; 5; 10; 15; 20; 25; 30; 35; 40; 45; 50; 55; 60; 65; 70; 75; 80; 85; 90; 95; 100; 105; 110; 115; 120; 125; 130; 135.
+ Để tìm bội của 9, ta lần lượt lấy 9 nhân với các số 0; 1; 2; 3;…
Một số bội của 9 là: 0; 18; 27; 36; 45; 54; 63; 72; 81; 90; 99; 108; 117; 126; 135.
Do đó 4 bội chung của 5 và 9 là: 0; 45; 90; 135.
Toán lớp 6 trang 54 Hoạt động 2: Quan sát bảng sau:
a) Viết ba bội chung của 8 và 12 theo thứ tự tăng dần.
c) Thực hiện phép chia ba bội chung của 8 và 12 cho BCNN(8, 12).
Lời giải:
a) Quan sát bảng ta thấy các bội chung của 8 và 12 là: 0; 24; 48; 72.
Đề bài chỉ yêu cầu chúng ta đưa ra 3 bội chung của 8 và 12 nên ta chỉ cần chọn 3 trong 4 số trên và xếp chúng theo thứ tự tăng dần.
Ví dụ: 24; 48; 72.
b) Trong các bội chung của 8 và 12 ở trên, ta thấy số 24 là số bé nhất và khác 0 nên BCNN(8, 12) = 24.
c) Chia 3 bội chung của 8 và 12 cho BCNN(8, 12)
24 : 24 = 1
48 : 24 = 2
72 : 24 = 3.
Lời giải:
Vì bội chung của a và b đều là bội của BCNN(a, b) = 300 nên ta đi tìm các bội của 300.
Ta có các bội của 300 là: 0; 300; 600; 900; 1 200; … (lấy 300 lần lượt nhân với 0, 1, 2, 3,…)
Vậy tất cả các số có ba chữ số là bội chung của a và b là: 300; 600; 900.
Toán lớp 6 trang 55 Hoạt động 3:
Ta có thể tìm BCNN(6, 8) theo các bước sau:
Bước 1. Phân tích 6 và 8 ra thừa số nguyên tố
6 = 2 . 3
8 = 2 . 2 . 2 = 23
Bước 2. Chọn ra các thừa số nguyên tố chung và các thừa số nguyên tố riêng của 6 và 8 lần lượt là 2 và 3.
Bước 3. Với mỗi thừa số nguyên tố 2 và 3, ta chọn lũy thừa với số mũ lớn nhất
+) Số mũ lớn nhất của 2 là 3; ta chọn 23.
+) Số mũ lớn nhất của 3 là 1; ta chọn 31.
Bước 4. Lấy tích của các lũy thừa đã chọn, ta nhận được bội chung nhỏ nhất cần tìm BCNN(6, 8) = 23 . 31 = 24.
Toán lớp 6 trang 56 Luyện tập 3: Tìm bội chung nhỏ nhất của 12, 18, 27.
Lời giải:
+ Ta phân tích các số 12, 18, 27 ra thừa số nguyên tố:
12 = 4 . 3 = 22 . 3
18 = 2 . 9 = 2 . 32
27 = 33
+ Các thừa số nguyên tố chung và riêng của 12, 18 và 27 là 2 và 3.
Số mũ lớn nhất của 2 là 2, số mũ lớn nhất của 3 là 3
Vậy BCNN(12, 18, 27) = 22 . 33 = 4 . 27 = 108.
Toán lớp 6 trang 56 Hoạt động 4: Thực hiện phép tính:
Lời giải:
+) Ở tiểu học, ta đã làm như sau:
Quy đồng mẫu hai phân số bằng cách chọn mẫu chung là tích của hai mẫu:
Mẫu chung = 12 . 18 = 216
Ta có:
.
Vậy .
+) Để tính tổng hai phân số trên, ta có thể làm như sau:
- Chọn mẫu chung là BCNN của các mẫu. Cụ thể:
Mẫu chung = BCNN(12, 18) = 36
- Tìm thừa số phụ của mỗi mẫu (bằng cách chia mẫu chung cho từng mẫu), ta có:
36 : 12 = 3; 36 : 18 = 2
- Sau khi nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng, ta cộng hai phân số có cùng mẫu:
.
Toán lớp 6 trang 57 Luyện tập 4: Thực hiện phép tính: .
Lời giải:
+ Để thực hiện phép tính, trước tiên ta đi tìm BCNN của 15, 25 và 10
Ta có: 15 = 3 . 5; 25 = 52 ; 10 = 2 . 5
Các thừa số nguyên tố chung và riêng của 15, 25, 10 là 2, 3 và 5; lần lượt tương ứng với các số mũ lớn nhất là 1; 1 và 2.
Khi đó: BCNN(15, 25, 10)
= 2 . 3 . 52 = 6 . 25 = 150
+ Ta có: 150 : 15 = 10;
150 : 25 = 6; 150 : 10 = 15
+ Khi đó:
;
Vậy
.
Bài tập
a) Hãy viết các ước của 7 và các ước của 8. Tìm ƯCLN(7, 8).
b) Hai số 7 và 8 có nguyên tố cùng nhau hay không? Vì sao?
c) Tìm BCNN(7, 8). So sánh bội chung nhỏ nhất với tích hai số 7 và 8.
Lời giải:
a) + Để tìm các ước của 7 ta lấy 7 lần lượt chia cho các số tự nhiên từ 1 đến 7, các phép chia hết là: 7 : 1 = 7; 7 : 7 = 1
Do đó: các ước của 7 là: 1; 7
+ Để tìm các ước của 8 ta lấy 8 lần lượt chia cho các số tự nhiên từ 1 đến 8, các phép chia hết là: 8 : 1 = 8; 8 : 2 = 4; 8 : 4 = 2; 8 : 8 = 1.
Các ước của 8 là: 1; 2; 4; 8.
+ Từ đó suy ra ƯC(7, 8) = 1 nên ƯCLN(7, 8) = 1.
b) Vì ƯCLN(7, 8) = 1 (theo câu a) nên hai số 7 và 8 là hai số nguyên tố cùng nhau.
c) Ta có: 7 = 71; 8 = 23
Các thừa số nguyên tố chung và riêng là 7 và 2 với số mũ cao nhất lần lượt là 1 và 3.
Do đó BCNN(7, 8) = 71 . 23 = 56
Mà 7 . 8 = 56
Hay ta nói bội chung nhỏ nhất của hai số nguyên tố cùng nhau 7 và 8 chính bằng tích của hai số 7 và 8.
Toán lớp 6 trang 57 Bài 2: Quan sát hai thanh sau:
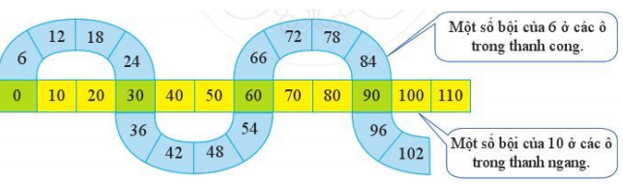 a) Số 0 có phải là bội chung của 6 và 10 không? Vì sao?
a) Số 0 có phải là bội chung của 6 và 10 không? Vì sao?
b) Viết bốn bội chung của 6 và 10 theo thứ tự tăng dần.
d) Tìm các bội chung của 6 và 10 mà nhỏ hơn 160.
Lời giải:
a) Quan sát hình trên, ta thấy số 0 nằm trên cả 2 thanh, thanh một số bội của 10 (thanh ngang) và thanh một số bội của 6 (thanh cong) nên số 0 là bội chung của 6 và 10.
Mở rộng: Hơn nữa, 0 chia hết cho tất cả các số tự nhiên khác 0 nên 0 là bội của mọi số tự nhiên khác 0.
b) Quan sát hình trên, ta thấy các số 0; 30; 60; 90 (được tô màu đậm hơn) nằm trên cả hai thanh ngang và thanh cong.
Do đó bốn bội chung của 6 và 10 được xếp theo thứ tự tăng dần là: 0; 30; 60; 90.
c) Trong các bội chung trên của 6 và 10, ta thấy 30 là số bé nhất và khác 0.
Do đó nó là bội chung nhỏ nhất của 6 và 10 hay BCNN(6, 10) = 30.
d) Các bội chung của 6 và 10 là các bội của BCNN(6, 10) = 30.
Mà các bội của 30 là: 0; 30; 60; 90; 120; 150; 180;…. (lần lượt nhân 30 với 0, 1, 2, …)
Vậy các bội chung của 6 và 10 nhỏ hơn 160 là: 0; 30; 60; 90; 120; 150.
Toán lớp 6 trang 58 Bài 3: Tìm bội chung nhỏ nhất của:
Lời giải:
a) Ta có, 7 và 13 đều là các số nguyên tố
Nên 7 và 13 cũng là hai số nguyên tố cùng nhau
Do đó: BCNN(7, 13) = 7 . 13 = 91.
b) Ta có: 54 = 2 . 27 = 2 . 33
108 = 4 . 27 = 22 . 33
Các thừa số nguyên tố chung và riêng của 54 và 108 là 2 và 3, tương ứng với các số mũ lớn nhất lần lượt là 2 và 3
Khi đó: BCNN(54, 108)
= 22 . 33 = 4 . 27 = 108.
c) Ta có: 21 = 3 . 7
30 = 3 . 10 = 3 . 2 . 5;
70 = 7. 10 = 7 . 2 . 5
Các thừa số nguyên tố chung và riêng của 21, 30, 70 là 2, 3, 5, 7; chúng đều có số mũ lớn nhất là 1.
Do đó: BCNN(21, 30, 70) = 2 . 3. 5 . 7 = 210.
Toán lớp 6 trang 58 Bài 4: Thực hiện phép tính sau:
Lời giải:
a) Để thực hiện phép tính, trước hết tìm bội chung nhỏ nhất của 48 và 40 để quy đồng mẫu số.
+ Ta có: 48 = 16 . 3 = 24 . 3
40 = 8 . 5 = 23 . 5
Các thừa số nguyên tố chung và riêng của 48 và 40 là 2, 3, 5, tương ứng với các số mũ lớn nhất lần lượt là 4, 1, 1.
Khi đó: BCNN(48, 40)
= 24 . 3 .5 = 16 . 3 . 5 = 240.
+ 240 : 48 = 5; 240 : 40 = 6
+ Ta có:
Vậy
b) Để thực hiện phép tính, trước hết tìm bội chung nhỏ nhất của 6, 27 và 18 để quy đồng mẫu số.
+ Ta có: 6 = 2 . 3; 27 = 33; 18 = 2 . 9 = 2 . 32
Các thừa số nguyên tố chung và riêng của 6, 27 và 18 là 2; 3, tương ứng với các số mũ lớn nhất là 1; 3.
Khi đó: BCNN(6, 27, 18) = 21 . 33 = 2 . 27 = 54
+ 54 : 6 = 9; 54 : 27 = 2; 54 : 18 = 3
+ Ta có:
;
Vậy
Lời giải:
Gọi số cần tìm là x
Ta có: BCNN(x, 5) = 45
Mà 45 = 5 . 9 = 5 . 32 ; 5 = 51 và 5 là số nguyên tố nên x và 5 phải là hai số nguyên tố cùng nhau, mà bội chung nhỏ nhất của hai số nguyên tố cùng nhau chính bằng tích của hai số đó.
Do đó x = 32 = 9.
Vậy số cần tìm là 9.
Lời giải:
Gọi a là số học sinh của câu lạc bộ thể thao
Vì khi chia số học sinh trong câu lạc bộ đó thành từng nhóm 5 học sinh hoặc 8 học sinh thì vừa hết nên a là bội chung của 5 và 8.
Ta có: 5 = 51; 8 = 23
Do đó: BCNN(5, 8) = 51 . 23 = 5 . 8 = 40
Mà bội chung của 5 và 8 là các bội của BCNN(5, 8) = 40
Nên BC(5, 8) ={0; 40; 80; 120; …}
Vì nên a = 40.
Vậy câu lạc bộ thể thao đó có 40 học sinh.
Lời giải:
Gọi x là số ngày ít nhất mà ba tàu lại cập cảng cùng nhau.
Vì tàu thứ nhất cứ 10 ngày thì cập cảng một lần nên x là bội của 10.
Tàu thứ hai cứ 12 ngày thì cập cảng một lần nên x là bội của 12.
Tàu thứ ba cứ 15 ngày thì cập cảng một lần nên x là bội của 15.
Do đó x là bội chung của 10, 12 và 15
Mà x là ít nhất nên x là bội chung nhỏ nhất của 10, 12 và 15.
Ta đi tìm BCNN(10, 12, 15)
Ta có: 10 = 2 . 5; 12 = 3 . 4 = 3 . 22; 15 = 3 . 5
Khi đó: BCNN(10, 12, 15) = 22 . 3 . 5 = 4 . 3 . 5 = 60
Hay x = 60
Vậy sau ít nhất 60 ngày thì ba tàu lại cùng nhau cập cảng.
Có thể em chưa biết
Toán lớp 6 trang 58 Có thể em chưa biết – Bài 1: Lịch can Chi
Giải thích tại sao cứ 60 năm thì năm Giáp Tý được lặp lại?
Lời giải:
Vì cứ 10 năm, can Giáp được lặp lại. Cứ 12 năm, chi Tý được lặp lại, nên số năm Giáp Tý được lặp lại là bội chung của 10 và 12. Và số năm ít nhất năm Giáp Tý lặp lại là bội chung nhỏ nhất của 10 và 12.
Phân tích 10 và 12 ra thừa số nguyên tố ta được:
10 = 2 . 5
12 = 2 . 2 . 3 = 22 . 3
Các thừa số nguyên tố chung và riêng của 10 và 12 là 2, 3, 5 với số mũ lớn nhất lần lượt là: 2, 1, 1.
Khi đó: BCNN(10, 12) = 22 . 3 . 5 = 60.
Vậy cứ sau 60 năm thì năm Giáp Tý được lặp lại.
Lý thuyết Toán 6 Bài 3: Bội chung và bội chung nhỏ nhất – Cánh diều
I. Bội chung và bội chung nhỏ nhất
1. Bội chung:
Số tự nhiên n được gọi là bội chung của hai số a và b nếu n vừa là bội của a vừa là bội của b.
Quy ước: Viết tắt bội chung là BC.
Kí hiệu: Tập hợp các bội chung của a và b là BC(a, b).
Ví dụ: Các bội của 2 là: 0, 2, 4, 6, 8, 10, 12,…
Các bội của 3 là: 0, 3, 6, 9, 12,…
Các bội chung của 2 và 3 là: 0, 6, 12, …
Vậy BC(2, 3) = {0; 6; 12; …}.
Chú ý: Số tự nhiên n được gọi là bội chung của ba số a, b, c nếu n là bội của cả ba số a, b, c. Ta kí hiệu: Tập hợp các bội chung của a, b, c là BC(a, b, c).
Ví dụ: 20 chia hết cho 2 nên 20 là bội của 2, 20 chia hết cho 4 nên 20 là bội của 4, 20 chia hết cho 5 nên 20 là bội của 5. Do đó 20 là một bội chung của ba số 2, 4, 5.
2. Bội chung nhỏ nhất:
Số nhỏ nhất khác 0 trong các bội chung của a và b được gọi là bội chung nhỏ nhất của a và b.
Quy ước: Viết tắt bội chung nhỏ nhất là BCNN.
Kí hiệu: bội chung nhỏ nhất của a và b là BCNN(a, b).
Ví dụ: Ta có các bội chung của 2 và 3 là: 0, 6, 12,… Số nhỏ nhất khác 0 trong các bội chung của 2 và 3 là 6 nên 6 là bội chung nhỏ nhất của 2 và 3.
Vậy BCNN(2, 3) = 6.
Chú ý:
+ Số nhỏ nhất khác 0 trong các bội chung của ba số a, b, c được gọi là bội chung nhỏ nhất của ba số a, b, c.
+ Kí hiệu: bội chung nhỏ nhất của a, b, c là BCNN(a, b, c).
+ Bội chung nhỏ nhất của hai số nguyên tố cùng nhau bằng tích của hai số đó.
Ví dụ: 5 và 8 là hai số nguyên tố cùng nhau nên BCNN(5, 8) = 5 . 8 = 40.
3. Tìm bội chung thông qua BCNN
+ Bội chung của nhiều số là bội của bội chung nhỏ nhất của chúng.
+ Để tìm bội chung của nhiều số, ta có thể lấy bội chung nhỏ nhất của chúng lần lượt nhân với 0, 1, 2, …
Ví dụ: Biết BCNN(a, b) = 30. Tìm tất cả các số có hai chữ số là bội chung của a và b.
Lời giải:
Vì bội chung của a và b đều là bội của BCNN(a, b) = 30 nên tất cả các số có hai chữ số là bội chung của a và b là: 30, 60, 90.
II. Tìm bội chung nhỏ nhất bằng cách phân tích các số ra thừa số nguyên tố
Các bước tìm BCNN bằng cách phân tích các số ra thừa số nguyên tố
Bước 1: Phân tích mỗi số ra thừa số nguyên tố
Bước 2: Chọn ra các thừa số nguyên tố chung và các thừa số nguyên tố riêng
Bước 3: Với mỗi thừa số nguyên tố chung và riêng, ta chọn lũy thừa với số mũ lớn nhất
Bước 4: Lấy tích của các lũy thừa đã chọn, ta nhận được bội chung nhỏ nhất cần tìm.
Ví dụ: Tìm BCNN(40, 48).
Lời giải:
Ta có: 40 = 23 . 5; 48 = 24 . 3
Chọn ra các thừa số nguyên tố chung và riêng của 40 và 48, đó là 2, 3, 5.
Số mũ lớn nhất của 2 là 4; Số mũ lớn nhất của 3 là 1; Số mũ lớn nhất của 5 là 1.
Vậy BCNN(40, 48) = 24 . 3 . 5 = 240.
Chú ý: Nếu thì BCNN(a, b) = a. Chẳng hạn: BCNN(48, 16) = 48.
III. Ứng dụng bội cung nhỏ nhất vào cộng, trừ các phân số không cùng mẫu
Để tính tổng (hoặc hiệu) hai hay nhiều phân số không cùng mẫu, ta có thể làm như sau:
+ Quy đồng mẫu số hai phân số bằng cách chọn mẫu chung là BCNN của các mẫu.
+ Tìm thừa số phụ của mỗi mẫu (bằng cách chia mẫu chung cho từng mẫu).
+ Sau khi nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng, ta cộng (trừ) hai hay nhiều phân số có cùng mẫu.
Ví dụ: Thực hiện phép tính:
Lời giải:
BCNN(32, 24, 48) = 96
96 : 32 = 3; 96 : 24 = 4; 96 : 48 = 2
Ta có:
Vậy .
Xem thêm lời giải bài tập Toán lớp 6 sách Cánh diều hay, chi tiết khác:
Bài 12: Ước chung và ước chung lớn nhất
Bài 13: Bội chung và bội chung nhỏ nhất
Xem thêm các chương trình khác:
- Soạn văn lớp 6 (hay nhất) - Cánh diều
- Soạn văn lớp 6 (ngắn nhất) - Cánh diều
- Bố cục tác phẩm Ngữ văn 6 – Cánh Diều
- Nội dung chính tác phẩm Ngữ văn lớp 6 – Cánh Diều
- Tóm tắt tác phẩm Ngữ văn lớp 6 – Cánh Diều
- Tác giả tác phẩm Ngữ văn lớp 6 – Cánh Diều
- Văn mẫu lớp 6 – Cánh Diều
- Giải VBT Luyện viết Ngữ văn lớp 6 – Cánh diều
- Giải sgk Lịch Sử 6 – Cánh Diều
- Giải sbt Lịch Sử 6 – Cánh Diều
- Giải VBT Lịch sử 6 – Cánh diều
- Lý thuyết Lịch sử lớp 6 – Cánh diều
- Giải sbt Địa Lí 6 – Cánh Diều
- Giải sgk Địa Lí 6 – Cánh Diều
- Lý thuyết Địa Lí 6 – Cánh Diều
- Giải VBT Địa lí 6 – Cánh diều
- Giải sgk GDCD 6 – Cánh Diều
- Lý thuyết GDCD 6 – Cánh diều
- Giải sbt Giáo dục công dân 6 – Cánh diều
- Giải sgk Công nghệ 6 – Cánh Diều
- Lý thuyết Công nghệ 6 – Cánh Diều
- Giải sgk Khoa học tự nhiên 6 – Cánh Diều
- Giải sbt Khoa học tự nhiên 6 – Cánh Diều
- Lý thuyết Khoa học tự nhiên 6 – Cánh Diều
- Giải sgk Tin học 6 – Cánh Diều
- Lý thuyết Tin học 6 – Cánh Diều
- Giải sgk Tiếng Anh 6 - ilearn Smart World
- Ngữ pháp Tiếng Anh 6 i-learn Smart World
- Trọn bộ Từ vựng Tiếng Anh 6 ilearn Smart World đầy đủ nhất
- Giải sbt Tiếng Anh 6 - iLearn Smart World
- Bài tập Tiếng Anh 6 iLearn Smart World theo Unit có đáp án



