Giải Toán 6 Bài 2 (Cánh diều): So sánh các phân số. Hỗn số dương

Mục lục Giải Toán 6 Bài 2: So sánh các phân số. Hỗn số dương

Giải Toán 6 trang 31 Tập 2

Câu hỏi khởi động trang 31 Toán 6 Tập 2: Ta đã biết $\frac{2}{5}<\frac{5}{9}$. Phải chăng $\frac{2}{-5}<\frac{-5}{9}$?

Lời giải

Sau bài học này ta sẽ trả lời được:

Vì $\frac{2}{5}<\frac{5}{9}$ nên $\frac{2}{-5}>\frac{-5}{9}$

Hoạt động 1 trang 31 Toán 6 Tập 2: So sánh:

a) –3 và 2

b) –8 và –5

Lời giải

a) Ta có –3 là số nguyên âm nên – 3 < 0, còn 2 là số nguyên dương nên 2 > 0. Do đó 2 > – 3.

b) Ta có số đối của – 8 là 8 và số đối của – 5 là 5 mà 5 < 8 nên – 5 > – 8.

Hoạt động 2 trang 31 Toán 6 Tập 2: So sánh: $\frac{2}{-5}$ và $\frac{-5}{9}$

Lời giải:

Để so sánh hai phân số $\frac{2}{-5}$ và $\frac{-5}{9}$, ta làm như sau:

Giải Toán 6 trang 32 Tập 2

Luyện tập vận dụng 1 trang 32 Toán 6 Tập 2: So sánh:

a) $\frac{7}{-11}$ và $\frac{8}{-11}$

b) $\frac{-5}{3}$ và $\frac{5}{-4}$

Lời giải

a) Ta có $\frac{7}{-11}=\frac{-7}{11}$ và $\frac{8}{-11}=\frac{-8}{11}.$

Vì – 8 < – 7 nên $\frac{-8}{11}<\frac{-7}{11}$ hay $\frac{8}{-11}<\frac{7}{-11}.$

Vậy $\frac{8}{-11}<\frac{7}{-11}.$

b) Ta có $\frac{5}{-4}=\frac{-5}{4};$

MTC = BCNN(3, 4) = 12. Khi đó, ta có:

$\frac{-5}{3}=\frac{-5.4}{3.4}=\frac{-20}{12};$

$\frac{-5}{4}=\frac{-5.3}{4.3}=\frac{-15}{12}.$

Vì – 20 < – 15 nên $\frac{-20}{12}<\frac{-15}{12}$ hay $\frac{5}{-4}<\frac{-5}{3}.$

Vậy $\frac{5}{-4}<\frac{-5}{3}.$

Hoạt động 3 trang 32 Toán 6 Tập 2:

a) Tìm thương và số dư trong phép chia 7 cho 4.

b) Viết phân số $\frac{7}{4}$ dưới dạng tổng của một số nguyên dương và một phân số bé hơn 1.

Lời giải

a) Ta thực hiện đặt tính:

Suy ra 7 : 4 = 1 (dư 3).

Vậy thương của phép chia là 1 và số dư là 3.

b) Vì 7 : 4 = 1 (dư 3) nên 7 = 4.1 + 3, Khi đó, ta có:

$\frac{7}{4}=\frac{4.1+3}{4}=\frac{4.1}{4}+\frac{3}{4}=1+\frac{3}{4}.$

Vậy $\frac{7}{4}=1+\frac{3}{4}.$

Giải Toán 6 trang 33 Tập 2

Luyện tập vận dụng 2 trang 33 Toán 6 Tập 2:

a) Viết mỗi phân số sau thành hỗn số: $\frac{14}{3};\frac{22}{7}$.

b) Viết mỗi hỗn số sau thành phân số: $2\frac{3}{4};5\frac{1}{6}$.

Lời giải

a) Ta có: $\frac{14}{3}=\frac{4.3+2}{3}=\frac{4.3}{3}+\frac{2}{3}=4+\frac{2}{3}=4\frac{2}{3};$

$\frac{22}{7}=\frac{3.7+1}{7}=\frac{3.7}{7}+\frac{1}{7}=3+\frac{1}{7}=3\frac{1}{7}.$

Vậy các phân số $\frac{14}{3};\frac{22}{7}$ được viết dưới dạng hỗn số lần lượt là: $4\frac{2}{3}; 3\frac{1}{7}.$

b) Ta có:

$2\frac{3}{4}=\frac{2.4+3}{4}=\frac{8+3}{4}=\frac{11}{4};$

$5\frac{1}{6}=\frac{5.6+1}{6}=\frac{30+1}{6}=\frac{31}{6}.$

Vậy các hỗn số $2\frac{3}{4}; 5\frac{1}{6}$ được viết dưới dạng phân số lần lượt là: $\frac{11}{4};\frac{31}{6}.$

Bài tập

Bài 1 trang 33 Toán 6 Tập 2: So sánh:

a) $\frac{-9}{4}$và $\frac{1}{3}$.

b) $\frac{-8}{3}$ và $\frac{4}{-7}$.

c) $\frac{9}{-5}$ và $\frac{7}{-10}$

Lời giải

a) Cách 1: Hai phân số không cùng mẫu, nên ta sẽ thực hiện quy đồng mẫu hai phân số trước:

Ta có: MTC = BCNN(4,3) = 12. Khi đó:

$\frac{-9}{4}=\frac{-9.3}{4.3}=\frac{-27}{12};$

$\frac{1}{3}=\frac{1.4}{3.4}=\frac{4}{12}.$

Vì – 27 < 4 nên $\frac{-27}{12}<\frac{4}{12}$ hay $\frac{-9}{4}<\frac{1}{3}$.

Vậy $\frac{-9}{4}<\frac{1}{3}$.

Cách 2: So sánh hai phân số với 0.

Ta có –9 < 0 nên $\frac{-9}{4}<\frac{0}{4}=0;$

Ta có 0 < 1 nên $0=\frac{0}{3}<\frac{1}{3}$.

Suy ra $\frac{-9}{4}<0<\frac{1}{3}.$

Vậy $\frac{-9}{4}<\frac{1}{3}.$

b) $\frac{-8}{3}$và $\frac{4}{-7}$

Ta có: $\frac{4}{-7}=\frac{-4}{7}.$

Hai phân số đã cho chưa cùng mẫu nên ta sẽ thực hiện quy đồng hai phân số trước.

MTC = BCNN(3, 7) = 3.7 = 21. Khi đó, ta có:

$\frac{-8}{3}=\frac{-8.7}{3.7}=\frac{-56}{21};$

$\frac{-4}{7}=\frac{-4.3}{7.3}=\frac{-12}{21}.$

Vì – 56 < –12 nên $\frac{-56}{21}<\frac{-12}{21}$ hay $\frac{-8}{3}<\frac{4}{-7}.$

Vậy $\frac{-8}{3}<\frac{4}{-7}.$

c) Ta có: $\frac{9}{-5}=\frac{-9}{5}$ và $\frac{7}{-10}=\frac{-7}{10}$

Hai phân số chưa cùng mẫu nên ta sẽ thực hiện quy đồng mẫu trước rồi so sánh sau.

MTC = BCNN(5, 10) = 10. Khi đó, ta có:

$\frac{-9}{5}=\frac{-9.2}{5.2}=\frac{-18}{10};$

Vì –18 < –7 nên $\frac{-18}{10}<\frac{-7}{10}$ hay $\frac{9}{-5}<\frac{7}{-10}.$

Vậy $\frac{9}{-5}<\frac{7}{-10}.$

Bài 2 trang 33 Toán 6 Tập 2: Viết các phân số sau theo thứ tự tăng dần:

a) $\frac{2}{5}; \frac{-1}{2}; \frac{2}{7}$.

b) $\frac{12}{5}; \frac{-7}{3}; \frac{-11}{4}$

Lời giải

a) Ta chia thành hai nhóm:

Nhóm 1: Nhóm gồm các phân số âm: $\frac{-1}{2};$

Nhóm 2: Nhóm gồm các phân số dương: $\frac{2}{5}; \frac{2}{7}.$

Ta chỉ cần so sánh hai phân số ở nhóm 2 với nhau:

Ta có MTC = BCNN(5, 7) = 35. Khi đó, ta có:

$\frac{2}{5}=\frac{2.7}{5.7}=\frac{14}{35};$

$\frac{2}{7}=\frac{2.5}{7.5}=\frac{10}{35}.$

Vì 10 < 14 nên $\frac{10}{35}<\frac{14}{35}$ hay $\frac{2}{7}<\frac{2}{5}.$

Vì các phân số ở nhóm 1 luôn nhỏ hơn nhóm 2 nên ta có: $\frac{-1}{2}<\frac{2}{7}<\frac{2}{5}.$

Vậy các phân số theo thứ tự tăng dần là: $\frac{-1}{2};\frac{2}{7};\frac{2}{5}.$

b) Ta chia thành hai nhóm:

Nhóm 1: Nhóm gồm các phân số âm: $\frac{-7}{3};\frac{-11}{4}$

Nhóm 2: Nhóm gồm các phân số dương: $\frac{12}{5}$

Ta chỉ cần so sánh hai phân số ở nhóm 1 với nhau:

Ta có MTC = BCNN(3, 4) = 12. Khi đó, ta có:

$\frac{-7}{3}=\frac{-7.4}{3.4}=\frac{-28}{12};$

$\frac{-11}{4}=\frac{-11.3}{4.3}=\frac{-33}{12}.$

Vì –33 < –28 nên $\frac{-33}{12}<\frac{-28}{12}$ hay $\frac{-11}{4}<\frac{-7}{3}.$

Vì các phân số ở nhóm 1 luôn nhỏ hơn nhóm 2 nên ta có: $\frac{-11}{4}<\frac{-7}{3}<\frac{12}{5}.$

Vậy các phân số theo thứ tự tăng dần là: $\frac{-11}{4};\frac{-7}{3};\frac{12}{5}.$

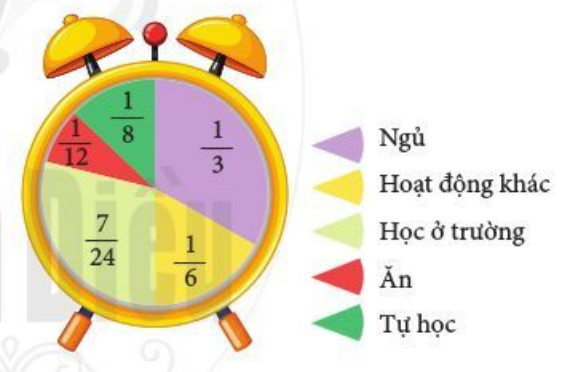
Bài 3 trang 33 Toán 6 Tập 2: Bạn Hà thể hiện thời gian trong ngày của mình như hình vẽ bên.

a) Hỏi bạn Hà dành thời gian cho hoạt động nào nhiều nhất? Ít nhất?

b) Hãy sắp xếp các số trên hình vẽ theo thứ tự giảm dần.

Lời giải

a) Quan sát hình vẽ ta thấy: phần thời gian màu tím là to nhất và phần thời gian màu đỏ là nhỏ nhất. Do đó:

Bạn Hà dành thời gian cho hoạt động ngủ là nhiều nhất. và thời gian cho hoạt động ăn là ít nhất.

b) Các phân số chưa chung mẫu nên ta sẽ thực hiện quy đồng mẫu thức trước.

Ta có: 8 = 2³, 3 = 3, 6 = 2.3, 24 = 2³.3, 12 = 2².3.

Do đó MTC = BCNN(8, 3, 6, 24, 12) = 2³.3 = 8.3 = 24. Khi đó, ta có:

$\frac{1}{8}=\frac{1.3}{8.3}=\frac{3}{24};$

$\frac{1}{3}=\frac{1.8}{3.8}=\frac{8}{24};$

$\frac{1}{6}=\frac{1.4}{6.4}=\frac{4}{24};$

$\frac{7}{24};$

$\frac{1}{12}=\frac{1.2}{12.2}=\frac{2}{24}.$

Vì 8 > 7 > 4 > 3 > 2 nên

$\frac{8}{24}>\frac{7}{24}>\frac{4}{24}>\frac{3}{24}>\frac{2}{24}$

hay

$\frac{1}{3}>\frac{7}{24}>\frac{1}{6}>\frac{1}{8}>\frac{1}{12}.$

Vậy các phân số trên hình được sắp xếp theo thứ tự giảm dần là:

$\frac{1}{3};\frac{7}{24};\frac{1}{6};\frac{1}{8};\frac{1}{12}.$

Bài 4 trang 33 Toán 6 Tập 2:

a) Viết các số đo thời gian dưới dạng hỗn số với đơn vị là giờ:

2 giờ 15 phút; 10 giờ 20 phút.

b) Viết các số đo diện tích sau dưới dạng hỗn số với đơn vị là héc–ta (biết 1 ha = 100 a):

1 ha 7 a; 3 ha 50 a.

Lời giải

a) Đổi 15 phút = $\frac{15}{60}$ giờ = $\frac{1}{4}$ giờ

Suy ra 2 giờ 15 phút = $2 + \frac{1}{4}$ giờ = $2\frac{1}{4}$ giờ.

Vậy 2 giờ 15 phút = $2\frac{1}{4}$ giờ.

Đổi 20 phút = $\frac{20}{60}$ giờ = $\frac{1}{3}$ giờ

Suy ra 10 giờ 20 phút = $10 + \frac{1}{3}$ giờ = $10\frac{1}{3}$ giờ.

Vậy 10 giờ 20 phút = $10\frac{1}{3}$ giờ.

b) Đổi 7 a = $\frac{7}{100}$ ha,

Suy ra 1 ha 7 a = $1 +\frac{7}{100}$ ha = $1\frac{7}{100}$ha.

Vậy 1 ha 7 a = $1\frac{7}{100}$ ha.

Đổi 50 a = $\frac{50}{100}$ ha = $\frac{1}{2}$ ha

Suy ra 3 ha 50 a = $3 +\hspace{0.17em}\frac{1}{2}$ ha = $3\frac{1}{2}$ ha.

Vậy 3 ha 50 a = $3 +\hspace{0.17em}\frac{1}{2}$ ha = $3\frac{1}{2}$ ha.

Bài 5 trang 33 Toán 6 Tập 2: Chọn số thích hợp cho $\boxed{?}$:

a)$\frac{-11}{15}<\frac{\boxed{?}}{15}<\frac{\boxed{?}}{15}<\frac{-8}{15}$;

b) $\frac{-1}{3}<\frac{\boxed{?}}{36}<\frac{\boxed{?}}{18}<\frac{-1}{4}$;

c) $\frac{4}{-12}>\frac{\boxed{?}}{-12}>\frac{\boxed{?}}{-12}>\frac{7}{-12}$;

d) $\frac{-1}{-4}>\frac{-1}{\boxed{?}}>\frac{-1}{\boxed{?}}>\frac{1}{7}$.

Lời giải

a) Gọi hai số cần điền là x và y, khi đó ta có:

$\frac{-11}{15}<\frac{\boxed{x}}{15}<\frac{\boxed{y}}{15}<\frac{-8}{15}$

Suy ra –11 < x < y < – 8

Mà $\mathrm{x},\mathrm{y}\in \mathrm{\mathbb{Z}}$

Do đó x = – 10, y = –9

Vậy ta điền: $\frac{-11}{15}<\frac{\boxed{-10}}{15}<\frac{\boxed{-9}}{15}<\frac{-8}{15}$.

b) Gọi hai số cần điền là m và n. Khi đó, ta có:

$\frac{-1}{3}<\frac{\boxed{\mathrm{m}}}{36}<\frac{\boxed{\mathrm{n}}}{18}<\frac{-1}{4}$

Muốn tìm m và n ta cần so sánh được các tử số với nhau. Do đó ta cần quy đồng mẫu số các phân số trên.

MTC = BCNN(3, 36, 18, 4) = 36. Khi đó, ta có:

$\frac{-12}{36}<\frac{\boxed{\mathrm{m}}}{36}<\frac{\boxed{2\mathrm{n}}}{36}<\frac{-9}{36}$

Suy ra: –12 < m < 2n < –9

Mà $\mathrm{m},\mathrm{n}\in \mathrm{\mathbb{Z}}$

Do đó m = –11, 2n = –10

Suy ra m = –11, n = –10:2 = –5.

Vậy ta điền: $\frac{-1}{3}<\frac{\boxed{-11}}{36}<\frac{\boxed{-5}}{18}<\frac{-1}{4}$.

c) Gọi hai số cần điền là p và q. Khi đó, ta có:

$\frac{4}{-12}>\frac{\boxed{\mathrm{p}}}{-12}>\frac{\boxed{\mathrm{q}}}{-12}>\frac{7}{-12}$

$\Rightarrow \frac{-4}{12}>\frac{\boxed{-\mathrm{p}}}{12}>\frac{\boxed{-\mathrm{q}}}{12}>\frac{-7}{12}$

$\Rightarrow$– 4 > – p > – q > – 7

Mà $\mathrm{p},\mathrm{q}\in \mathrm{\mathbb{Z}}$ nên – p = –5, –q = – 6 hay p = 5 và q = 6.

Vậy ta điền: $\frac{4}{-12}>\frac{\boxed{5}}{-12}>\frac{\boxed{6}}{-12}>\frac{7}{-12}.$

d) $\frac{-1}{-4}>\frac{-1}{\boxed{?}}>\frac{-1}{\boxed{?}}>\frac{1}{7}$.

Gọi hai số cần điền là z và t. Khi đó, ta có:

$\frac{-1}{-4}>\frac{-1}{\boxed{\mathrm{z}}}>\frac{-1}{\boxed{\mathrm{t}}}>\frac{1}{7}$

Muốn tìm z và t ta cần so sánh được các mẫu số với nhau. Do đó ta cần đưa các phân số trên về cùng tử số.

Ta thấy ba phân số đầu đều có chung tử số là – 1, nên ta chỉ cần chuyển phân số cuối về tử – 1 như sau: $\frac{1}{7}=\frac{-1}{-7}$. Khi đó, ta có:

$\frac{-1}{-4}>\frac{-1}{\boxed{\mathrm{z}}}>\frac{-1}{\boxed{\mathrm{t}}}>\frac{-1}{-7}$

$\Rightarrow$–4 > z > t > – 7

Mà $\mathrm{z},\mathrm{t}\in \mathrm{\mathbb{Z}}$ nên z = – 5, t = – 6.

Vậy ta điền: $\frac{-1}{-4}>\frac{-1}{\boxed{-5}}>\frac{-1}{\boxed{-6}}>\frac{1}{7}$.

Lý thuyết Toán 6 Bài 2: So sánh các phân số. Hỗn số dương đơn giản - Cánh diều

1. So sánh các phân số

a) So sánh hai phân số

Trong hai phân số khác nhau luôn có một phân số nhỏ hơn phân số kia.

- Nếu phân số $\frac{a}{b}$ nhỏ hơn phân số $\frac{c}{d}$ thì ta viết $\frac{a}{b}<\frac{c}{d}$ hay $\frac{c}{d}>\frac{a}{b}.$

- Phân số lớn hơn 0 gọi là phân số dương.

- Phân số nhỏ hơn 0 gọi là phân số âm.

- Nếu $\frac{a}{b}<\frac{c}{d}$ và $\frac{c}{d}<\frac{e}{g}$ thì $\frac{a}{b}<\frac{e}{g}.$

b) Cách so sánh hai phân số

* So sánh hai phân số cùng mẫu

Trong hai phân số có cùng một mẫu dương, phân số nào có tử lớn hơn thì lớn hơn.

Ví dụ 1. So sánh hai phân số $\frac{1}{3}$ và $\frac{2}{3}$.

Hướng dẫn giải

Ta thấy hai phân số trên cùng mẫu số là 3, tử số của hai phân số là 1 < 2

Nên $\frac{1}{3}<\frac{2}{3}$ hay $\frac{2}{3}>\frac{1}{3}.$

Chú ý: Với hai phân số có cùng một mẫu nguyên âm, ta đưa chúng về hai phân số có cùng mẫu nguyên dương rồi so sánh.

Ví dụ 2. So sánh hai phân số $\frac{1}{-3}$ và $\frac{-2}{-3}$

Hướng dẫn giải

Ta có: $\frac{1}{-3}=\frac{-1}{3}$ và $\frac{-2}{-3}=\frac{2}{3}$

Hai phân số có cùng mẫu số là 3, tử số của hai phân số là ‒1 < 2 nên $\frac{-1}{3}<\frac{2}{3}$.

Do đó $\frac{1}{-3}<\frac{-2}{-3}$.

*So sánh hai phân số không cùng mẫu

Để so sánh hai phân số không cùng mẫu, ta quy đồng mẫu hai phân số đó (về cùng một mẫu dương) rồi so sánh các tử với nhau. Phân số nào có tử lớn hơn thì phân số đó lớn hơn.

Bước 1: Quy đồng mẫu hai phân số đã cho (về cùng một mẫu dương)

Bước 2: So sánh tử của các phân số: Phân số nào có tử lớn hơn thì phân số đó lớn hơn.

Ví dụ 3. So sánh hai phân số $\frac{-3}{8}$ và $\frac{5}{-7}$.

Hướng dẫn giải

Ta có $\frac{5}{-7}=\frac{-5}{7}=\frac{\left(-5\right).8}{7.8}=\frac{-40}{56}$ và $\frac{-3}{8}=\frac{\left(-3\right).7}{8.7}=\frac{-21}{56}$

Do ‒40 < ‒21 nên $\frac{-40}{56}<\frac{-21}{56}$.

Vậy $\frac{5}{-7}<\frac{-3}{8}.$

2. Hỗn số dương

Viết một phân số lớn hơn 1 thành tổng của một số nguyên dương và một phân số nhỏ hơn 1 (với tử và mẫu dương) rồi viết chúng liền nhau thì được 1 hỗn số dương.

Ví dụ 4.

a) Phân số $\frac{13}{3}=\frac{4.3+1}{3}=\frac{4.3}{3}+\frac{1}{3}=4+\frac{1}{3}=4\frac{1}{3}.$

Do đó phân số $\frac{13}{3}$ còn được viết dưới dạng hỗn số là $4\frac{1}{3}.$

b) Hỗn số $2\frac{3}{4}=2+\frac{3}{4}=\frac{2.4}{4}+\frac{3}{4}=\frac{8+3}{4}=\frac{11}{4}$.

Do đó hỗn số $2\frac{3}{4}$ viết dưới dạng phân số là $\frac{11}{4}.$

Xem thêm lời giải bài tập Toán lớp 6 sách Cánh diều hay, chi tiết khác:

Bài 3: Phép cộng. Phép trừ phân số

Bài 4: Phép nhân, phép chia phân số

Bài 5: Số thập phân

Bài 6: Phép cộng, phép trừ số thập phân

Bài 7: Phép nhân, phép chia số thập phân