Giải Toán 6 Bài tập cuối chương 5 (Cánh diều)

Giải Toán 6 trang 71 Tập 2

Bài 1 trang 71 Toán 6 Tập 2: Viết các số sau theo thứ tự tăng dần:

a) $\frac{-3}{4};\frac{2}{5};\frac{-2}{3};\frac{1}{3}$.

b) – 3,175; 1,9; – 3,169; 1,89.

Lời giải

a) Ta chia các phân số thành hai nhóm:

– Nhóm 1 gồm các phân số âm $\frac{-3}{4};\frac{-2}{3}.$

– Nhóm 2 gồm các phân số dương $\frac{2}{5};\frac{1}{3}.$

Ở nhóm 1, để so sánh hai phân số này ta cần quy đồng:

Ta có: $\frac{-3}{4}=\frac{-3.3}{4.3}=\frac{-9}{12};$

$\frac{-2}{3}=\frac{-2.4}{3.4}=\frac{-8}{12}.$

Vì – 9 < – 8 nên $\frac{-9}{12}<\frac{-8}{12}$ hay $\frac{-3}{4}<\frac{-2}{3}.$

Ở nhóm 2, để so sánh hai phân số này ta cần quy đồng:

Ta có: $\frac{2}{5}=\frac{2.3}{5.3}=\frac{6}{15};$

$\frac{1}{3}=\frac{1.5}{3.5}=\frac{5}{15}.$

Vì 6 > 5 nên $\frac{6}{15}>\frac{5}{15}$ hay $\frac{1}{3}<\frac{2}{5}.$

Suy ra $\frac{-3}{4}<\frac{-2}{3}<\frac{1}{3}<\frac{2}{5}.$

Vậy các phân số được sắp xếp theo thứ tự tăng dần là: $\frac{-3}{4};\frac{-2}{3};\frac{1}{3};\frac{2}{5}.$

b) – 3,175; 1,9; – 3,169; 1,89.

Ta chia các số thập phân thành hai nhóm:

– Nhóm 1: Gồm các số thập phân âm: – 3,175 và – 3,169.

– Nhóm 2: Gồm các số thập phân dương: 1,9 và 1,89.

Ở nhóm 1, Số đối của số thập phân – 3,175 là 3,175 và số đối của số thập phân – 3,169 là 3,169.

Ta có 3 = 3, kể từ trái sang phải cặp chữ số cùng hàng ở sau dấu phẩy đầu tiên khác nhau là cặp chữ số ở vị trí hàng phần trăm. Do 7 > 6 nên 3,175 > 3,169 hay – 3,175 < – 3,169.

Ở nhóm 2, Ta có 1 = 1 và kể từ trái sang phải cặp chữ số cùng hàng ở sau dấu phẩy đầu tiên khác nhau là cặp chữ số ở vị trí hàng phần mười. Do 9 > 8 nên 1,9 > 1,89.

Suy ra – 3, 175 < – 3,169 < 1, 89 < 1,9.

Vậy các số thập phân theo thứ tự tăng dần là: –3,175; –3,169; 1,89 và 1,9.

Bài 2 trang 71 Toán 6 Tập 2: Tính một cách hợp lí:

a) $\left(\frac{617}{191}+\frac{29}{33}-\frac{115}{117}\right).\left(\frac{1}{4}-\frac{1}{5}-\frac{1}{20}\right)$;

b) $\frac{12}{5}.\left(\frac{10}{3}-\frac{5}{12}\right)$;

c) 1,23 – 5,48 + 8,77 – 4,32;

d) 7 . 0,25 + 9 . 0,25.

Lời giải

a) $\left(\frac{617}{191}+\frac{29}{33}-\frac{115}{117}\right).\left(\frac{1}{4}-\frac{1}{5}-\frac{1}{20}\right)$

$=\left(\frac{617}{191}+\frac{29}{33}-\frac{115}{117}\right).\left(\frac{5}{20}-\frac{4}{20}-\frac{1}{20}\right)$

$=\left(\frac{617}{191}+\frac{29}{33}-\frac{115}{117}\right).\left(\frac{5-4-1}{20}\right)$

$=\left(\frac{617}{191}+\frac{29}{33}-\frac{115}{117}\right).0$

= 0.

b) $\frac{12}{5}.\left(\frac{10}{3}-\frac{5}{12}\right)$

$=\frac{12}{5}.\left(\frac{40}{12}-\frac{5}{12}\right)$

$=\frac{12}{5}.\left(\frac{40-5}{12}\right)$

$=\frac{12}{5}.\frac{35}{12}$

= 7.

c) 1,23 – 5,48 + 8,77 – 4,32

= (1,23 + 8,77) + (–5,48 – 4,32)

= 10 + ( –10)

= 0.

d) 7.0,25 + 9.0,25

= 0,25. (7 + 9)

= 0,25.16

= 4.

Bài 3 trang 71 Toán 6 Tập 2: Trong tháng Tư, gia đình bà Mai quản lí tài chính như sau:

– Thu nhập: 16 000 000 đồng;

– Chỉ tiêu: 13 000 000 đồng;

– Để dành: 3 000 000 đồng.

Tháng Năm thu nhập gia đình bà giảm 12% nhưng chỉ tiêu lại tăng l2% so với tháng Tư. Gia đình bà Mai trong tháng Năm còn để dành được bao nhiêu tiền hay thiếu bao nhiêu tiền?

Lời giải

Thu nhập tháng năm của gia đình bà Mai là: l6 000 000 – 16 000 000.12% = 14 080 000 (đồng).

Chi tiêu tháng năm của gia đình bà Mai là: 13 000 000 + 13 000 000.12% = 14 560 000 (đồng).

Gia đình bà Mai trong tháng Năm còn để dành được: 14 080 000 – 14 560 000 = – 480 000 (đồng).

Vậy gia đình bà Mai trong tháng Năm còn thiếu 480 000 đồng.

Bài 4 trang 71 Toán 6 Tập 2: Theo https://danso.org/viet–nam vào ngày 11/02/2020, dân số của Việt Nam là 97 912 500 người. Giả thiết rằng tỉ lệ gia tăng dân số hằng năm của Việt Nam luôn (xấp xỉ) là 2%. Hãy làm tròn số chỉ dân số của Việt Nam đến hàng phần trăm (theo đơn vị: triệu người):

Bài 5 trang 71 Toán 6 Tập 2: Bạn Dũng đọc một quyển sách trong 3 ngày: ngày thứ nhất đọc được $\frac{1}{3}$số trang, ngày thứ hai đọc được $\frac{5}{8}$ số trang còn lại, ngày thứ ba đọc nốt 30 trang cuối cùng. Quyển sách đó có bao nhiêu trang?

Bài 6 trang 71 Toán 6 Tập 2: Ông Ba muốn lát gạch và trồng cỏ cho sân vườn. Biết diện tích phần trồng cỏ bằng $\frac{1}{5}$ diện tích sân vườn và diện tích phần lát gạch là 36 m².

Giải Toán 6 trang 72 Tập 2

Bài 7 trang 72 Toán 6 Tập 2: Người ta cũng sử dụng foot (đọc là phút, số nhiều là feet, kí hiệu là ft). là một đơn vị đo chiều dài, 1 ft = 304,8 mm. Người ta cũng sử dụng độ Fahrenhei (đọc là Fa–ren–hai, kí hiệu là F) để đo nhiệt độ. Công thức đổi từ độ C sang độ F là: F = (160 + 9C) : 5, trong đó C là nhiệt độ theo độ C và F là nhiệt độ tương ứng theo độ F.

a) Tính nhiệt độ của nước sôi theo độ F, biết rằng nước sôi có nhiệt độ là 100 °C.

b) Nhiệt độ mặt đường nhựa vào buổi trưa những ngày hè nắng gắt ở Hà Nội có thể lên đến 109 °F. Hãy tính (xấp xỉ) nhiệt độ của mặt đường nhựa vào thời điểm đó theo độ C.

c) Điểm sôi của nước bị ảnh hưởng bởi những thay đổi về độ cao. Theo tính toán, địa hình cứ cao lên 1 km thì điểm sôi của nước giảm đi (khoảng) 3°C. Tìm điểm sôi của nước (tính theo độ F) tại độ cao 5 000 ft.

Lời giải

a) Nhiệt độ sôi của nước là 100⁰C nghĩa là C = 100, chuyển sang nhiệt độ F là:

F = (160 + 9.100) : 5 = 212⁰F.

Vậy nhiệt độ sôi của nước biểu diễn theo độ F là 212⁰F.

b) Nhiệt độ của mặt đường nhựa vào buổi trưa là 109⁰F nghĩa là F = 109.

Khi đó, ta có: 109 = (160 + 9.C) : 5

160 + 9C = 109.5

160 + 9C = 545

9C = 545 – 160

9C = 385

C = 385 : 9

C $\approx$ 42,8.

Vậy vào buổi trưa những ngày hè nắng gắt ở Hà Nội nhiệt độ mặt đường nhựa vào buổi trưa có thể lên đến 42,8⁰C.

c) Ta có: 1 ft = 304,8 mm

5 000 ft = 1 524 000 mm = 1,524 km.

Cứ lên cao 1 km thì nhiệt độ giảm khoảng 3⁰C nên ở độ 1,524 thì nhiệt độ giảm khoảng:

3.1,524 = 4,572⁰C.

Suy ra nhiệt độ sôi của nước tại độ cao này là: 100 – 4,572 = 95,428⁰C.

Chuyển sang độ F là: F = (160 + 9.95,428) : 5 = 203,7704⁰F.

Vậy điểm sôi của nước tại độ cao 5 000 ft là 203,7704⁰F.

Bài 8 trang 72 Toán 6 Tập 2: Theo kế hoạch, Tập đoàn Dầu khí Quốc gia Việt Nam khai thác 12,37 triệu tấn dầu thô trong năm 2019.

a) Hãy tính thể tích của lượng dầu thô khai thác năm 2019 theo kế hoạch, biết rằng khối lượng riêng của dầu thô (lấy tròn) là 900 kg/m³ và thể tích của một chất thì bằng khối lượng của chất đó chia cho khối lượng riêng của nó.

b) Giả sử chúng ta phải vận chuyển hết lượng dầu thô khai thác năm 2019 đến các nhà máy lọc dầu bằng các tàu chở dầu thô có tải trọng 104 530 DWT (viết tắt của cụm từ tiếng Anh Deadweigit Tonnage, là đơn vị đo năng lực vận tải an toàn của tàu thuỷ). Biết rằng 1 DWT tương đương với 1,13 m³ (thể tích của khoang chứa dầu thô của tàu chở dầu). Cần ít nhất bao nhiêu chuyến tàu chở dầu thô như thế?

Lời giải

12 370 000 000: 900 $\approx$ 13 744 444,4 (m³).

Vậy thể tích của lượng dầu thô khai thác năm 2019 theo kế hoạch là 13 744 444,4 m³.

b) Đổi 13 744 444,4 m³ = 12 163 225,17 (DWT).

Ta có: 12 163 225,2 : 104 503 $\approx$ 116,4.

Do đó cần ít nhất 117 chuyến tàu chở dầu thô như thế.

Vậy cần ít nhất 117 chuyến tàu chở dầu thô như thế.

Bài 9 trang 72 Toán 6 Tập 2: Hai cửa hàng bán xôi cho học sinh ăn sáng. Biểu đồ trong Hình 3 cho biết số học sinh ăn xôi ở mỗi cửa hàng trong một tuần.

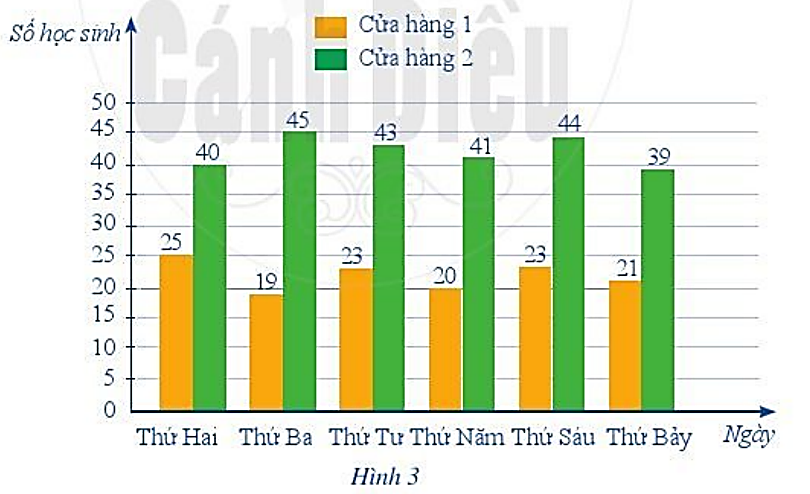
a) Số học sinh ăn xôi nhiều nhất trong một ngày là bao nhiêu?

b) Số học sinh ăn xôi ít nhất trong một ngày là bao nhiêu?

c) Cửa hàng 2 bán được nhiều hơn Cửa hàng 1 bao nhiêu suất xôi trong tuần đó?

d) Mỗi buổi sáng hai cửa hàng nên chuẩn bị khoảng bao nhiêu suất xôi cho học sinh?

Lời giải

Trong ngày thứ hai, số học sinh ăn xôi là: 25 + 40 = 65 (học sinh).

Trong ngày thứ ba, số học sinh ăn xôi là: 19 + 45 = 64 (học sinh).

Trong ngày thứ tư, số học sinh ăn xôi là: 23 + 43 = 66 (học sinh).

Trong ngày thứ năm, số học sinh ăn xôi là: 20 + 41 = 61 (học sinh).

Trong ngày thứ sáu, số học sinh ăn xôi là: 23 + 44 = 67 (học sinh).

Trong ngày thứ bảy, số học sinh ăn xôi là: 21 + 39 = 60 (học sinh).

a) Số học sinh ăn xôi nhiều nhất trong một ngày là ở ngày thứ sáu với 67 học sinh.

Vậy số học sinh ăn xôi nhiều nhất trong một ngày là 67 học sinh.

b) Số học sinh ăn xôi ít nhất trong một ngày là ở ngày thứ năm với 61 học sinh.

Vậy số học sinh ăn xôi ít nhất trong một ngày là 61 học sinh.

c) Trong một tuần, cửa hàng 1 bán được số suất xôi là:

25 + 19 + 23 + 20 + 23 + 21 = 131 (suất).

Trong một tuần, cửa hàng 2 bán được số suất xôi là:

40 + 45 + 43 + 41 + 44 + 39 = 252 (suất).

Trong tuần đó, cửa hàng 2 bán được nhiều hơn Cửa hàng 1 số suất xôi là:

252 – 131 = 121 (suất).

Vậy trong tuần đó, cửa hàng 2 bán được nhiều hơn Cửa hàng 1 121 suất xôi.

d) Mỗi buổi sáng Cửa hàng 1 nên chuẩn bị khoảng:

$\frac{25+19+23+20+23+21}{6}=\frac{131}{6}\approx 21,83.$

Mối buổi sáng Cửa hàng 2 nên chuẩn bị khoảng:

$\frac{40+45+43+41+44+39}{6}=\frac{252}{6}=42.$

Vậy mỗi sáng Cửa hàng 1 nên chuẩn bị khoảng 22 suất, Cửa hàng 2 nên chuẩn bị khoảng 42 suất.

Lý thuyết Toán 6 Ôn tập Chương 5 - Cánh diều

1. Phân số với tử số và mẫu số là số nguyên

a) Khái niệm phân số

Kết quả của phép chia số nguyên a cho số nguyên b khác 0 có thể viết dưới dạng $\frac{a}{b}.$

Ta gọi $\frac{a}{b}$ là phân số.

Phân số $\frac{a}{b}$ đọc là: a phần b, a là tử số (còn gọi tắt là tử), b là mẫu số (còn gọi tắt là mẫu).

Chú ý: Mọi số nguyên a có thể viết dưới dạng phân số là $\frac{a}{1}.$

b) Phân số bằng nhau

Khái niệm hai phân số bằng nhau: Hai phân số được gọi là bằng nhau nếu chúng cùng biểu diễn một giá trị.

Quy tắc bằng nhau của hai phân số:

Xét hai phân số $\frac{a}{b}$ và $\frac{c}{d}$.

Nếu $\frac{a}{b}=\frac{c}{d}$ thì a.d = b.c. Ngược lại, nếu a.d = b.c thì $\frac{a}{b}=\frac{c}{d}$.

Chú ý: Với a, b là hai số nguyên và b ≠ 0, ta luôn có: $\frac{a}{-b}=\frac{-a}{b}$ và $\frac{-a}{-b}=\frac{a}{b}$.

c) Tính chất cơ bản của phân số

* Tính chất cơ bản

- Nếu ta nhân cả tử và mẫu của một phân số với cùng một số nguyên khác 0 thì ta được một phân số bằng phân số đã cho.

$\frac{a}{b}=\frac{a.m}{b.m}$ với $m\in \mathbb{Z}$, m ≠ 0.

- Nếu ta chia cả tử và mẫu của một phân số cho cùng một ước chung của chúng thì ta được một phân số bằng phân số đã cho.

$\frac{a}{b}=\frac{a:n}{b:n}$ với m $\in$ ƯC(a, b).

Chú ý: Mỗi phân số đều đưa được về một phân số bằng nó và có mẫu là số dương.

* Rút gọn về phân số tối giản

Dựa vào tính chất cơ bản của phân số, để rút gọn phân số với tử và mẫu là số nguyên về phân số tối giản ta thường làm như sau:

Bước 1: Tìm ƯCLN của tử và mẫu sau khi đã bỏ dấu “– “ (nếu có)

Bước 2: Chia cả tử và mẫu cho ước chung lớn nhất (ƯCLN) vừa tìm được, ta có phân số tối giản cần tìm.

* Quy đồng mẫu nhiều phân số

Để quy đồng nhiều phân số, ta thường làm như sau:

Bước 1: Viết các phân số đã cho dưới dạng phân số có mẫu dương. Tìm bội chung nhỏ nhất (BCNN) của các mẫu dương đó để làm mẫu số chung.

Bước 2: Tìm thừa số phụ của mỗi mẫu, bằng cách chia mẫu chung cho từng mẫu.

Bước 3: Nhân tử và mẫu của mỗi phân số ở Bước 1 với thừa số phụ tương ứng.

2. So sánh các phân số. Hỗn số dương

a) So sánh các phân số

* So sánh hai phân số

Trong hai phân số khác nhau luôn có một phân số nhỏ hơn phân số kia.

- Nếu phân số $\frac{a}{b}$ nhỏ hơn phân số $\frac{c}{d}$ thì ta viết $\frac{a}{b}<\frac{c}{d}$ hay $\frac{c}{d}>\frac{a}{b}.$

- Phân số lớn hơn 0 gọi là phân số dương.

- Phân số nhỏ hơn 0 gọi là phân số âm.

- Nếu $\frac{a}{b}<\frac{c}{d}$ và $\frac{c}{d}<\frac{e}{g}$ thì $\frac{a}{b}<\frac{e}{g}.$

* Cách so sánh hai phân số

- So sánh hai phân số cùng mẫu

Trong hai phân số có cùng một mẫu dương, phân số nào có tử lớn hơn thì lớn hơn.

Chú ý: Với hai phân số có cùng một mẫu nguyên âm, ta đưa chúng về hai phân số có cùng mẫu nguyên dương rồi so sánh.

- So sánh hai phân số không cùng mẫu

Để so sánh hai phân số không cùng mẫu, ta quy đồng mẫu hai phân số đó (về cùng một mẫu dương) rồi so sánh các tử với nhau. Phân số nào có tử lớn hơn thì phân số đó lớn hơn.

Bước 1: Quy đồng mẫu hai phân số đã cho (về cùng một mẫu dương)

Bước 2: So sánh tử của các phân số: Phân số nào có tử lớn hơn thì phân số đó lớn hơn.

b) Hỗn số dương

Viết một phân số lớn hơn 1 thành tổng của một số nguyên dương và một phân số nhỏ hơn 1 (với tử và mẫu dương) rồi viết chúng liền nhau thì được 1 hỗn số dương.

3. Phép cộng, phép trừ phân số.

a) Phép cộng phân số

* Quy tắc cộng hai phân số

- Quy tắc cộng hai phân số cùng mẫu

Muốn cộng hai phân số có cùng mẫu số, ta cộng tử số với nhau và giữ nguyên mẫu số.

$\frac{a}{m}+\frac{b}{m}=\frac{a+b}{m}$

- Quy tắc cộng hai phân số không cùng mẫu

Muốn cộng hai phân số không cùng mẫu, ta quy đồng mẫu những phân số đó rồi cộng các tử và giữ nguyên mẫu chung.

* Tính chất của phép cộng phân số

Tương tự phép cộng các số tự nhiên, phép cộng phân số cũng có các tính chất: giao hoán, kết hợp, cộng với số 0.

Trong thực hành, ta có thể sử dụng các tính chất này để tính giá trị biểu thức một cách hợp lí.

b) Phép trừ phân số

* Số đối của một phân số

- Số đối của phân số $\frac{a}{b}$ kí hiệu là $-\frac{a}{b}$. Ta có: $\frac{a}{b}+\left(-\frac{a}{b}\right)=0$

Chú ý: Ta có: $-\frac{a}{b}=\frac{a}{-b}=\frac{-a}{b}$ với $a,b\in \mathbb{Z},$ b ≠ 0.

Số đối của $-\frac{a}{b}$ là $\frac{a}{b}$, tức là $-\left(-\frac{a}{b}\right)=\frac{a}{b}.$

* Quy tắc trừ hai phân số

- Muốn trừ hai phân số có cùng mẫu, ta trừ tử của số bị trừ cho tử của số trừ và giữ nguyên mẫu.

$\frac{a}{m}-\frac{b}{m}=\frac{a-b}{m}$.

- Muốn trừ hai phân số không cùng mẫu, ta quy đồng mẫu những phân số đó rồi trừ tử của số bị trừ cho tử của số trừ và giữ nguyên mẫu chung.

- Muốn trừ hai phân số, ta cộng số bị trừ với số đối của số trừ:

$\frac{a}{b}-\frac{c}{d}=\frac{a}{b}+\left(-\frac{c}{d}\right).$

c) Quy tắc dấu ngoặc

- Khi bỏ dấu ngoặc có dấu cộng “+” đằng trước, ta giữ nguyên dấu các số hạng trong ngoặc.

- Khi bỏ dấu ngoặc có dấu trừ “‒“ đằng trước, ta phải đổi dấu của các số hạng trong ngoặc: dấu “+” thành dấu “‒“ và dấu “‒“ thành dấu “+”.

$\frac{a}{b}-\left(\frac{c}{d}+\frac{e}{f}-\frac{g}{h}\right)=\frac{a}{b}-\frac{c}{d}-\frac{e}{f}+\frac{g}{h}$

4. Phép nhân, phép chia phân số

a) Phép nhân phân số

* Quy tắc nhân hai phân số

- Muốn nhân hai phân số, ta nhân các tử số với nhau và nhân các mẫu với nhau.

$\frac{a}{b}.\frac{c}{d}=\frac{a.c}{b.d}$ với b ≠ 0 và d ≠ 0.

- Muốn nhân một số nguyên với một phân số (hoặc nhân một phân số với một số nguyên), ta nhân số nguyên với tử của phân số và giữ nguyên mẫu của phân số đó:

$m.\frac{a}{b}=\frac{m.a}{b};\frac{a}{b}.n=\frac{a.n}{b}$ với b ≠ 0.

* Tính chất của phép nhân phân số

- Tính chất giao hoán: $\frac{a}{b}.\frac{c}{d}=\frac{c}{d}.\frac{a}{b}$;

- Tính chất kết hợp: $\left(\frac{a}{b}.\frac{c}{d}\right).\frac{p}{q}=\frac{a}{b}.\left(\frac{c}{d}.\frac{p}{q}\right)$;

- Nhân với số 1” $\frac{a}{b}.1=1.\frac{a}{b}=\frac{a}{b}$;

- Nhân với số 0: $\frac{a}{b}.0=0.\frac{a}{b}=0$;

- Tính chất phân phối của phép nhân đối với phép cộng: $\frac{a}{b}.\left(\frac{c}{d}+\frac{p}{q}\right)=\frac{a}{b}.\frac{c}{d}+\frac{a}{b}.\frac{p}{q}$;

- Tính chất phân phối của phép nhân đối với phép trừ: $\frac{a}{b}.\left(\frac{c}{d}-\frac{p}{q}\right)=\frac{a}{b}.\frac{c}{d}-\frac{a}{b}.\frac{p}{q}$.

b) Phép chia phân số

* Phân số nghịch đảo

Phân số $\frac{b}{a}$ được gọi là phân số nghịch đảo của phân số $\frac{a}{b}$ với a ≠ 0 và b ≠ 0.

Chú ý: Tích của một phân số với phân số nghịch đảo của nó thì bằng 1.

* Phép chia phân số

Muốn chia một phân số cho một phân số khác 0, ta nhân số bị chia với phân số nghịch đảo của số chia:

$\frac{a}{b}:\frac{c}{d}=\frac{a}{b}.\frac{d}{c}=\frac{a.d}{b.c}$ với b, c, d khác 0.

c) Thứ tự thực hiện phép tính với phân số:

* Thứ tự thực hiện phép tính với phân số trong biểu thức không chứa dấu ngoặc:

Đối với biểu thức không chứa dấu ngoặc, ta thực hiện theo thứ tự:

Luỹ thừa → Phép nhân và phép chia → Phép cộng và phép trừ.

* Thứ tự thực hiện phép tính với phân số trong biểu thức có chứa dấu ngoặc:

Đối với biểu thức có chứa dấu ngoặc, ta thực hiện theo thứ tự:

Dấu ngoặc () → Dấu ngoặc [] → Dấu ngoặc {}.

5. Số thập phân

a) Số thập phân

- Phân số thập phân là phân số mà mẫu là lũy thừa của 10 và tử là số nguyên.

- Phân số thập phân có thể viết được dưới dạng số thập phân.

- Số thập phân gồm hai phần:

+ Phần số nguyên được viết bên trái dấu phẩy;

+ Phần thập phân được viết bên phải dấu phẩy.

b) So sánh các số thập phân

* So sánh hai số thập phân

Trong 2 số thập phân khác nhau luôn có một số nhỏ hơn số kia.

- Nếu số thập phân a nhỏ hơn số thập phân b thì ta viết a < b hay b > a.

- Số thập phân lớn hơn 0 gọi là số thập phân dương.

- Số thập phân nhỏ hơn 0 gọi là số thập phân âm.

- Nếu a < b và b < c thì a < c.

* Cách so sánh hai số thập phân

- So sánh hai số thập phân khác dấu:

Số thập phân âm luôn nhỏ hơn số thập phân dương.

- So sánh hai số thập phân dương:

Bước 1: So sánh phần số nguyên của hai số thập phân dương đó. Số thập phân nào có phần số nguyên lớn hơn thì lớn hơn.

Bước 2: Nếu 2 số thập phân dương đó có phần số nguyên bằng nhau thì ta tiếp tục so sánh từng cặp chữ số ở cùng một hàng (sau dấu ","), kể từ trái sang phải cho đến khi xuất hiện cặp chữ số đầu tiên khác nhau. Ở cặp chữ số khác nhau đó, chữ số nào lớn hơn thì số thập phân chứa chữ số đó lớn hơn.

- So sánh hai số thập phân âm:

Nếu a < b thì ‒ a > ‒ b.

6. Phép cộng, phép trừ số thập phân

a) Số đối của số thập phân

Số đối của số thập phân a kí hiệu là ‒a. Ta có: a + (‒a) = 0.

Chú ý: Số đối của số thập phân ‒a là a, tức là ‒(‒a) = a.

b) Phép cộng, phép trừ số thập phân

* Cộng hai số thập phân

- Cộng hai số thập phân dương: Muốn cộng hai số thập phân dương ta thực hiện quy tắc cộng hai số nguyên dương.

- Cộng hai số thập phân âm: Muốn cộng hai số thập phân âm ta cộng hai số đối của chúng rồi thêm dấu “‒” đằng trước kết quả:

(‒a) + (‒b) = ‒(a + b)

- Cộng hai số thập phân khác dấu, ta làm như sau:

+ Nếu số dương lớn hơn hay bằng số đối của số âm thì lấy số dương trừ đi số đối của số âm.

+ Nếu số dương nhỏ hơn số đối của số âm thì ta lấy số đối của số âm trừ đi số dương rồi thêm dấu trừ “‒” trước kết quả.

- Tính chất của phép cộng số thập phân:

Giống như phép cộng số nguyên, phép cộng số thập phân có các tính chất giao hoán, kết hợp, cộng với số 0, cộng với số đối.

* Trừ hai số thập phân

- Muốn trừ hai số thập phân, ta cộng số bị trừ với số đối của số trừ.

a – b = a + (–b)

c) Quy tắc dấu ngoặc

- Khi bỏ dấu ngoặc có dấu cộng “+” đằng trước, ta giữ nguyên dấu các số hạng trong ngoặc.

- Khi bỏ dấu ngoặc có dấu trừ “‒“ đằng trước, ta phải đổi dấu của các số hạng trong ngoặc: dấu “+” thành dấu “‒“ và dấu “‒“ thành dấu “+”:

a ‒ (b + c – d) = a ‒ b ‒ c + d

7. Phép nhân, phép chia số thập phân

a) Phép nhân số thập phân

* Nhân hai số thập phân

Muốn nhân hai số thập phân dương, ta làm như sau:

Bước 1: Viết thừa số này ở dưới thừa số kia như đối với phép nhân các số tự nhiên

Bước 2: Thực hiện phép nhân như nhân số tự nhiên

Bước 3: Đếm xem trong phần thập phân ở cả hai thừa số có tất cả bao nhiêu chữ số rồi dùng dấu “,” tách ở tích ra bấy nhiêu chữ số từ phải sang trái, ta nhận được tích cần tìm.

Chú ý: Hai số thập phân cùng dấu thì tích là số dương; hai số thập phân khác dấu thì tích là số âm.

Nhân hai số thập phân cùng dấu: (‒a) . (‒b) = a.b với a, b > 0

Nhân hai số thập phân khác dấu: (‒a) . b = a.(‒b) = ‒ (a.b) với a, b > 0

* Tính chất của phép nhân số thập phân

Phép nhân số thập phân cũng có các tính chất như phép nhân số nguyên: giao hoán, kết hợp, nhân với số 1, phân phối của phép nhân với phép cộng và phép trừ.

b) Phép chia số thập phân

Muốn chia hai số thập phân dương, ta làm như sau:

Bước 1: Số chia có bao nhiêu chữ số sau dấu “,” thì chuyển dấu “,” ở số bị chia sang bên phải bấy nhiêu chữ số. (Khi chuyển dấu “,” ở số bị chia sang phải mà số bị chia không đủ vị trí, thì ta điền thêm những chữ số 0 vào bên phải của số đó)

Bước 2: Bỏ đi dấu “,” ở số chia, ta nhận được số nguyên dương

Bước 3: Đem số nhận được ở Bước 1 chia cho số nguyên dương nhận được ở Bước 2, ta có thương cần tìm.

Chú ý: Hai số thập phân cùng dấu thì thương là số dương; hai số thập phân khác dấu thì thương là số âm.

Chia hai số thập phân cùng dấu: (‒a) : (‒b) = a : b với a, b > 0

Chia hai số thập phân khác dấu: (‒a) : b = a : (‒b) = ‒ (a : b) với a, b > 0

c) Thứ tự thực hiện phép tính với số thập phân:

* Thứ tự thực hiện phép tính với số thập phân trong biểu thức không chứa dấu ngoặc:

Đối với biểu thức không chứa dấu ngoặc, ta thực hiện theo thứ tự:

Luỹ thừa → Phép nhân và phép chia → Phép cộng và phép trừ.

* Thứ tự thực hiện phép tính với số thập phân trong biểu thức có chứa dấu ngoặc:

Đối với biểu thức có chứa dấu ngoặc, ta thực hiện theo thứ tự:

Dấu ngoặc () → Dấu ngoặc [] → Dấu ngoặc {}.

8. Ước lượng và làm tròn số

a) Làm tròn số nguyên

Để làm tròn một số nguyên (có nhiều chữ số) đến một hàng nào đó, ta làm như sau:

- Nếu chữ số đứng ngay bên phải hàng làm tròn nhỏ hơn 5 thì ta thay lần lượt các chữ số đứng bên phải hàng làm tròn bởi chữ số 0.

- Nếu chữ số đứng ngày bên phải hàng làm tròn lớn hơn hoặc bằng 5 thì ta cộng thêm 1 vào chữ số của hàng làm tròn rồi thay lần lượt các chữ số đứng bên phải hàng làm tròn bởi chữ số 0.

Chú ý: Kí hiệu “≈” đọc là “gần bằng” hoặc “xấp xỉ”.

b) Làm tròn số thập phân

Để làm tròn một số thập phân dương đến một hàng nào đó (gọi là hàng làm tròn), ta làm như sau:

- Tìm chữ số hàng làm tròn

- Nhìn sang chữ số ngay bên phải

+ Nếu chữ số đó nhỏ hơn 5 thì giữ nguyên chữ số hàng làm tròn và thay tất cả các chữ số bên phải bằng số 0 và bỏ đi nếu chúng ở phần thập phân.

+ Nếu chữ số đó lớn hơn hay bằng 5 thì tăng chữ số hàng làm tròn thêm 1 rồi thay tất cả các chữ số bên phải bằng 0 hoặc bỏ đi nếu chũng ở phấn thập phân.

c) Ước lượng kết quả các phép tính

Để ước lượng kết quả các phép tính ta thực hiện làm tròn các số trong phép tính.

9. Tỉ số. Tỉ số phần trăm

a)Tỉ số

* Tỉ số của hai số

Tỉ số của a và b (b ≠ 0) là thương trong phép chia số a cho số b, kí hiệu là a : b hoặc $\frac{a}{b}$.

Chú ý:

- Nếu tỉ số của a và b được viết dưới dạng $\frac{a}{b}$ thì ta cũng gọi a là tử số và b là mẫu số.

- Tỉ số của số a và số b phải được viết theo đúng thứ tự là $\frac{a}{b}$ hoặc a : b.

- Tỉ số $\frac{a}{b}$ là phân số nếu cả tử a và mẫu b đều là số nguyên.

* Tỉ số của hai đại lượng (cùng loại và cùng đơn vị đo)

Tỉ số của hai đại lượng (cùng loại và cùng đơn vị đo) là tỉ số giữa hai số đo của hai đại lượng đó.

Nhận xét: Tỉ số của hai đại lượng thể hiện độ lớn của đai lượng này so với đại lượng kia.

a : b = $2\frac{3}{5}:\frac{9}{10}=\frac{13}{5}.\frac{10}{9}=\frac{26}{9}$.

b) Tỉ số phần trăm

* Tỉ số phần trăm của hai số

- Tỉ số phần trăm của a và b là $\frac{a}{b}.100\%$.

- Để tính tỉ số phần trăm của a và b, ta làm như sau:

+ Bước 1: Viết tỉ số $\frac{a}{b}$

+ Bước 2: Tính số $\frac{a.100}{b}$ và viết thêm % vào bên phải số vừa nhận được.

Nhận xét: Có hai cách tính $\frac{a.100}{b}$ là:

- Chia a cho b để tìm thương (ở dạng số thập phân) rồi lấy thương đó nhân với 100.

- Nhân a với 100 rồi chia cho b, viết thương nhận được ở dạng số nguyên hoặc số thập phân.

Chú ý: Khi tính tỉ số phần trăm của a và b mà phải làm tròn số thập phân thì ta kàn theo cách nhân a với 100 rồi chia cho b, viết thương nhận được ở dạng số nguyên hoặc số thập phân.

* Tỉ số phần trăm của hai đại lượng (cùng loại và cùng đơn vị đo)

Tỉ số phần trăm của hai đại lượng (cùng loại và cùng đơn vị đo) là tỉ số phần trăm giữa hai số đo của hai đại lượng đó.

Tỉ số phần trăm của đại lượng thứ nhất có số đo (đại lượng) a và đại lượng thứ hai có số đo (đại lượng) b là: $\frac{a.100}{b}\%$.

10. Bài toán về hai phân số

a) Tìm giá trị phân số của một số cho trước

- Muốn tìm giá trị $\frac{m}{n}$ của số a cho trước, ta tính $a.\frac{m}{n}$ $\left(m\in \mathbb{N},n\in \mathbb{N}*\right)$ .

Giá trị của m% của số a là giá trị phân số $\frac{m}{100}$ của số

- Muốn tìm giá trị m% của số a cho trước, ta tính $a.\frac{m}{100}\left(m\in \mathbb{N}*\right)$.

b) Tìm một số biết giá trị phân số của số đó

- Muốn tìm một số biết $\frac{m}{n}$ của nó bằng a, ta tính $a:\frac{m}{n}\left(m,n\in \mathbb{N}*\right)$.

- Muốn tìm một số biết m% của nó bằng a, ta tính $a:\frac{m}{100}\left(m\in \mathbb{N}*\right)$.

Xem thêm lời giải bài tập Toán lớp 6 sách Cánh diều hay, chi tiết khác:

Hoạt động thực hành và trải nghiệm. Chủ đề 2. Chỉ số khối cơ thể (BMI)

Bài 1: Điểm. Đường thẳng

Bài 2: Hai đường thẳng cắt nhau. Hai đường thẳng song song

Bài 3: Đoạn thẳng

Bài 4: Tia