Giải Toán 6 Bài 2 (Cánh diều): Tập hợp các số nguyên – Cánh diều
Lời giải bài tập Toán lớp 6 Bài 2: Tập hợp các số nguyên âm sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 6.
Giải Toán 6 Bài 2: Tập hợp các số nguyên
 a) Viết tập hợp các số chỉ nhiệt độ trong bản tin dự báo thời tiết ở trên.
a) Viết tập hợp các số chỉ nhiệt độ trong bản tin dự báo thời tiết ở trên.
b) Tập hợp đó gồm các loại số nào?
Lời giải:
a) Các số chỉ nhiệt độ trong bản tin dự báo thời tiết ở trên theo thứ tự từ thứ hai đến chủ nhật là: 0; 2; – 2; – 5; 1; 11; 6.
Gọi A là tập hợp các số chỉ nhiệt độ trong bản tin dự báo thời tiết trên.
Khi đó ta viết tập hợp A là:
A = {0; 2; – 2; – 5; 1; 11; 6}.
b) Tập hợp A gồm các loại số là: số nguyên âm và số tự nhiên.
+ Các số nguyên âm: – 2; – 5
+ Số tự nhiên: 0; 2; 1; 11; 6.
Toán lớp 6 trang 64 Luyện tập 1: Chọn kí hiệu “∈”; “∉” thích hợp cho ?:
Lời giải:
a) Ta có: số – 6 là số nguyên âm nên nó thuộc tập hợp các số nguyên.
Do đó ta viết: – 6 ∈ ℤ
b) Ta có: số – 10 là số nguyên âm nên nó không phải là số tự nhiên hay – 10 không thuộc tập hợp các số tự nhiên.
Do đó ta viết: – 10 ∉ ℕ
Toán lớp 6 trang 65 Hoạt động 2:
a) Quan sát Hình 3:
 Ta thấy:
Ta thấy:
+ Điểm – 5 (biểu diễn số nguyên – 5) nằm bên trái điểm gốc 0; cách điểm gốc 5 khoảng.
+ Điểm – 4 (biểu diễn số nguyên – 4) nằm bên trái điểm gốc 0, cách điểm gốc 4 khoảng.
+ Điểm – 2 (biểu diễn số nguyên – 2) nằm bên trái điểm gốc 0, cách điểm gốc 2 khoảng.
+ Điểm 3 (biểu diễn số nguyên 3) nằm bên phải điểm gốc 0, cách điểm gốc 3 khoảng.
+ Điểm 5 (biểu diễn số nguyên 5) nằm bên phải điểm gốc 0, cách điểm gốc 5 khoảng.
b)
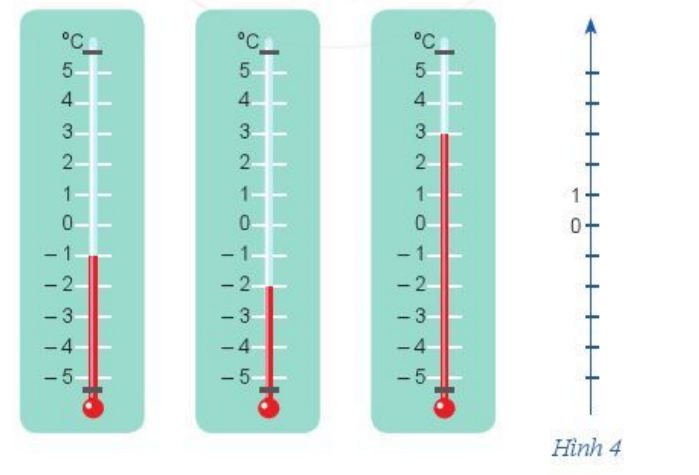
+ Quan sát Hình 4, ta thấy số đo nhiệt độ được chỉ trong mỗi hình theo thứ tự từ trái qua phải lần lượt là: – 1 °C, – 2 °C, 3 °C.
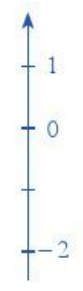
+ Biểu diễn các số lên trục số thẳng đứng ở Hình 4 ta được:
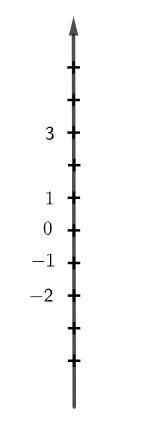
Lời giải:
Đề bài chỉ nói đến trục số mà không nói gì thêm nên ta hiểu đây là trục số nằm ngang.
Do đó ta có trục số sau:
 Các điểm A, B, C, D, E, F lần lượt biểu diễn các số – 7, – 6, – 4, 0, 2, 4.
Các điểm A, B, C, D, E, F lần lượt biểu diễn các số – 7, – 6, – 4, 0, 2, 4.
Toán lớp 6 trang 66 Hoạt động 3:
Quan sát trục số và trả lời các câu hỏi:
 a) Điểm biểu diễn số 4 cách điểm gốc 0 bao nhiêu đơn vị?
a) Điểm biểu diễn số 4 cách điểm gốc 0 bao nhiêu đơn vị?
b) Điểm biểu diễn số – 4 cách điểm gốc 0 bao nhiêu đơn vị?
c) Có nhận xét gì về khoảng cách từ điểm biểu diễn các số – 4 và 4 đến điểm gốc 0?
Lời giải:
Quan sát trục số ta thấy:
a) Điểm biểu diễn số 4 cách điểm gốc 0 một khoảng là 4 đơn vị.
b) Điểm biểu diễn số – 4 cách điểm gốc 0 một khoảng là 4 đơn vị.
c) Theo câu a và b ta có khoảng cách từ điểm biểu diễn các số – 4 và 4 đến điểm gốc 0 là bằng nhau.
Toán lớp 6 trang 67 Luyện tập: Cho ví dụ về hai số nguyên đối nhau và hai số nguyên không đối nhau.
Lời giải:
Đối với bài tập này, chúng ta có nhiều có thể đưa ra nhiều ví dụ khác nhau. Chẳng hạn, ta có:
+) Số 25 và – 25 là hai số nguyên đối nhau.
+) Số 5 và 15 không phải là hai số nguyên đối nhau.
Toán lớp 6 trang 67 Hoạt động 4:
b) Quan sát hai điểm – 2 và 1 trên trục số thẳng đứng và cho biết điểm – 2 nằm
phía dưới hay phía trên điểm 1.
Lời giải:
a) Quan sát hai điểm – 3 và 2 trên trục số nằm ngang, ta thấy điểm – 3 nằm bên trái điểm 2.
b) Quan sát hai điểm – 2 và 1 trên trục số thẳng đứng, ta thấy điểm – 2 nằm phía dưới điểm 1.
Toán lớp 6 trang 68 Luyện tập 4: Viết các số sau theo thứ tự tăng dần: – 6, – 12, 40, 0, – 18.
Lời giải:
Trong các số đã cho, ta có:
+ Các số nguyên âm là: – 6, – 12, – 18.
+ Số nguyên dương là: 40
Khi đó ta có: – 6 < 0, – 12 < 0, – 18 < 0 và 40 > 0 (vì các số nguyên âm luôn nhỏ hơn 0 và các số nguyên dương luôn lớn hơn 0).
Ta so sánh các số: – 6, – 12, – 18 bằng cách biểu diễn lên trục số thì ta được: – 18 < – 12 < – 6
Do đó ta có: – 18 < – 12 < – 6 < 0 < 40.
Vậy sắp xếp các số đã cho theo thứ tự tăng dần ta được: – 18,– 12, – 6, 0, 40.
Toán lớp 6 trang 68 Hoạt động 5: Biểu diễn các số – 6 và 4 trên trục số. Từ đó hãy so sánh – 6 và 4.
Lời giải:
+ Biểu diễn các số – 6 và 4 trên trục số:

Các điểm A và B theo thứ tự là các điểm biểu diễn của – 6 và 4 trên trục số.
+ Theo trục số ta thấy điểm – 6 nằm bên trái điểm 4 nên – 6 < 4.
Toán lớp 6 trang 68 Hoạt động 6: So sánh – 244 và – 25.
Lời giải:
Đề so sánh hai số nguyên âm – 244 và – 25, ta làm như sau:
|
Bước 1. Bỏ dấu "–" trước cả hai số – 244 và – 25 |
– 244 → 244 – 25 → 25 |
|
Bước 2. So sánh hai số nguyên dương nhận ở Bước 1: Số nguyên dương nào nhỏ hơn thì số nguyên âm ban đầu (trước khi bỏ dấu “–”) sẽ lớn hơn. |
Do 25 < 244 nên – 25 > – 244. |
Toán lớp 6 trang 69 Luyện tập 5: Viết các số sau theo thứ tự giảm dần: – 154, – 618, – 219, 58.
Lời giải:
+ Vì số nguyên dương luôn lớn hơn số nguyên âm, nên trong các số đã cho ta có 58 là số lớn nhất.
+ Ta so sánh các số nguyên âm: – 154, – 618, – 219
Số đối của các số – 154, – 618, – 219 lần lượt là 154, 618, 219.
Do 154 < 219 < 618 nên – 154 > – 219 > – 618
Do đó ta có: 58 > – 154 > – 219 > – 618.
Vậy sắp xếp các số đã cho theo thứ tự giảm dần ta được: 58, – 154, – 219, – 618.
Bài tập
a) Máy bay bay ở độ cao 10 000 m;
c) Tàu ngầm chạy dưới mực nước biển 100 m.
Lời giải:
Do ta viết các số nguyên biểu thị độ cao so với mực nước biển nên:
a) Máy bay bay ở độ cao 10 000 m, nghĩa là máy bay bay cao hơn mực nước biển là 10 000m. Do đó số nguyên biểu thị độ cao của máy bay ở đây là 10 000 m (hoặc ta cũng có thể viết + 10 000 m).
b) Tại mực nước biển là gốc nên số nguyên biểu thị độ cao ở mức nước biển là 0.
c) Tàu ngầm chạy dưới mực nước biển 100 m nên số nguyên biểu thị độ cao của tàu ngầm ở đây là – 100 m.
Toán lớp 6 trang 69 Bài 2: Chọn kí hiệu '' ∈'', " ∉" thích hợp cho ?:
Lời giải:
a) Ta có số – 3 là số nguyên âm nên nó thuộc tập hợp các số nguyên.
Do đó ta viết -3 ∈ ℤ
b) Ta có số 0 là số nguyên nên nó thuộc tập hợp các số nguyên.
Do đó ta viết 0 ∈ ℤ
c) Ta có số 4 là số nguyên dương nên nó cũng thuộc tập hợp các số nguyên.
Do đó ta viết 4 ∈ ℤ
d) Ta có số – 2 là số nguyên âm nên nó không phải là số tự nhiên hay – 2 không thuộc tập hợp các số tự nhiên.
Do đó ta viết -2 ∉ ℤ
Biểu diễn các số – 7, – 6, – 5, – 4, – 3, – 2, – 1, 0, 1, 2 vào các vạch tương ứng trên trục số đã cho, ta được:
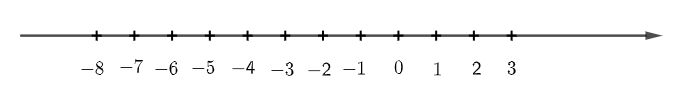
Toán lớp 6 trang 69 Bài 4: Quan sát trục số:
 a) Tính khoảng cách từ điểm O đến điểm A.
a) Tính khoảng cách từ điểm O đến điểm A.
b) Tìm trên trục số những điểm cách điểm O một khoảng là 5 đơn vị.
Lời giải:
a) Quan sát trục số đã cho, ta thấy điểm A cách điểm O là 2 khoảng
Hay khoảng cách từ điểm O tới điểm A là 2 đơn vị.
b) Ta có:

Vậy trên trục số những điểm cách điểm O một khoảng là 5 đơn vị là: điểm B (điểm – 5) và điểm C (điểm 5).
Lời giải:
Ta có:
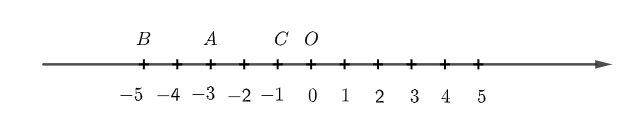 Các điểm A, B, C lần lượt là các điểm biểu diễn của các số nguyên – 3, – 5, – 1.
Các điểm A, B, C lần lượt là các điểm biểu diễn của các số nguyên – 3, – 5, – 1.
Ta có điểm B và C đều cách điểm A một khoảng là 2 đơn vị
Nên hai số nguyên có điểm biểu diễn cách điểm – 3 một khoảng là 2 đơn vị là – 5 và – 1.
Số đối của – 5 là 5; số đối của – 1 là 1.
Toán lớp 6 trang 69 Bài 6: So sánh các cặp số sau: 3 và 5; – 1 và – 3; – 5 và 2; 5 và – 3.
Lời giải:
Ta có thể so sánh các cặp số trên bằng một trong các cách sau:
Cách 1.
Biểu diễn các số đã cho lên trục số ta được:
 +) Ta thấy điểm 3 nằm bên trái điểm 5 nên 3 < 5.
+) Ta thấy điểm 3 nằm bên trái điểm 5 nên 3 < 5.
+) Điểm – 3 nằm bên trái điểm – 1 nên – 3 < – 1 hay – 1 > – 3.
+) Điểm – 5 nằm bên trái điểm 2 nên – 5 < 2.
+) Điểm – 3 nằm bên trái điểm 5 nên – 3 < 5 hay 5 > – 3.
Cách 2.
+) Ta có: 3 < 5 (so sánh hai số tự nhiên)
+) So sánh – 1 và – 3
Số đối của – 1 là 1; số đối của – 3 là 3.
Do 1 < 3 nên – 1 > – 3.
+) So sánh – 5 và 2
Vì – 5 là số nguyên âm và 2 là số nguyên dương nên – 5 < 2.
+) So sánh 5 và – 3
Vì 5 là số nguyên dương và – 3 là số nguyên âm nên 5 > – 3.
a) Ở nhiệt độ – 3 °C thì nước đóng băng.
b) Ở nhiệt độ 2 °C thì nước đóng băng.
Lời giải:
Nước đóng băng khi nhiệt độ từ 0 oC trở xuống hay nước đóng băng ở nhiệt độ bé hơn (nhỏ hơn) 0 oC.
a) Vì – 3 °C < 0 °C (số nguyên âm nhỏ luôn nhỏ hơn 0)
Do đó ở nhiệt độ – 3 °C thì nước đóng băng là phát biểu đúng.
b) Vì 2 °C > 0 °C (số nguyên dương luôn lớn hơn 0)
Do đó ở nhiệt độ 2 °C thì nước chưa thể đóng băng hay phát biểu "ở nhiệt độ 2 °C thì nước đóng băng" là phát biểu sai.
Lý thuyết Toán 6 Bài 2: Tập hợp các số nguyên – Cánh diều
I. Tập hợp ℤ các số nguyên
+ Số tự nhiên khác 0 còn được gọi là số nguyên dương.
+ Các số nguyên âm, số 0 và các số nguyên dương tạo thành tập hợp các số nguyên.
+ Tập hợp các số nguyên được kí hiệu là ℤ
Ví dụ:
+ Các số nguyên dương: 4, 6, 10 000, …
+ Tập hợp các số nguyên ℤ = {…, – 2, – 1, 0, 1, 2, …}
Chú ý:
+ Số 0 không phải số nguyên âm, cũng không phải số nguyên dương.
+ Các số nguyên dương 1, 2, 3,... đều mang dấu “+" nên còn được viết là + 1, + 2, + 3,...
II. Biểu diễn số nguyên trên trục số
Ta có thể biểu diễn số nguyên trên trục số. Có hai loại trục số:
1. Trục số nằm ngang
Trên trục số nằm ngang, điểm biểu diễn số nguyên âm nằm bên trái điểm 0, điểm biểu diễn số nguyên dương nằm bên phải điểm 0.

2. Trục số thẳng đứng
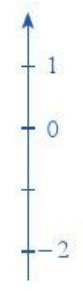
Trên trục số thẳng đứng, điểm biểu diễn số nguyên âm nằm phía dưới điểm 0, điểm biểu diễn số nguyên dương nằm phía trên điểm 0.
Chú ý: Khi nói “trục số” mà không nói gì thêm, ta hiểu là nói về trục số nằm ngang.
III. Số đối của một số nguyên

+ Trên trục số, hai số nguyên (phân biệt) có điểm biểu diễn nằm về hai phía của gốc 0 và cách đều gốc 0 được gọi là hai số đối nhau.
+ Số đối của 0 là 0.
Ví dụ:
– 4 và 4 là hai số đối nhau.
– 4 là số đối của 4 và 4 là số đối của – 4.
IV. So sánh các số nguyên
1. So sánh hai số nguyên
+ Trên trục số nằm ngang, nếu điểm a nằm bên trái điểm b thì số nguyên a nhỏ hơn số nguyên b.
+ Trên trục số thẳng đứng, nếu điểm a nằm phía dưới điểm b thì số nguyên a nhỏ hơn số nguyên b.
+ Nếu a nhỏ hơn b thì ta viết là a < b hoặc b > a.
Ví dụ:
![]()
Điểm – 10 nằm bến trái điểm – 5 nên – 10 < – 5
Điểm 2 nằm bên phải điểm 0 nên 2 > 0.
Chú ý:
+ Số nguyên dương luôn lớn hơn 0. Số nguyên âm luôn nhỏ hơn 0.
+ Nếu a < b và b < c thì a < c
Ví dụ: – 2 < 0 và 0 < 5 thì – 2 < 5.
2. Cách so sánh hai số nguyên
2.1 So sánh hai số nguyên khác dấu
Số nguyên âm luôn nhỏ hơn số nguyên dương.
Ví dụ: – 7 là số nguyên âm và 5 là số nguyên dương nên – 7 < 5.
2.2 So sánh hai số nguyên cùng dấu
+ So sánh hai số nguyên dương: Đã biết ở chương I.
+ So sánh hai số nguyên âm:
Để so sánh hai số nguyên âm, ta làm như sau:
Bước 1. Bỏ dấu “–” trước cả hai số âm
Bước 2. Trong hai số nguyên dương nhận được, số nào nhỏ hơn thì số nguyên âm ban đầu (trước khi bỏ dấu “–”) sẽ lớn hơn.
Ví dụ: So sánh – 216 và – 309.
Bỏ dấu “–” trước các số – 216 và – 309, ta được các số lần lượt là 216 và 309.
Do 216 < 309 nên – 216 > – 309.
Xem thêm lời giải bài tập Toán lớp 6 sách Cánh diều hay, chi tiết khác:
Xem thêm các chương trình khác:
- Soạn văn lớp 6 (hay nhất) - Cánh diều
- Soạn văn lớp 6 (ngắn nhất) - Cánh diều
- Bố cục tác phẩm Ngữ văn 6 – Cánh Diều
- Nội dung chính tác phẩm Ngữ văn lớp 6 – Cánh Diều
- Tóm tắt tác phẩm Ngữ văn lớp 6 – Cánh Diều
- Tác giả tác phẩm Ngữ văn lớp 6 – Cánh Diều
- Văn mẫu lớp 6 – Cánh Diều
- Giải VBT Luyện viết Ngữ văn lớp 6 – Cánh diều
- Giải sgk Lịch Sử 6 – Cánh Diều
- Giải sbt Lịch Sử 6 – Cánh Diều
- Giải VBT Lịch sử 6 – Cánh diều
- Lý thuyết Lịch sử lớp 6 – Cánh diều
- Giải sbt Địa Lí 6 – Cánh Diều
- Giải sgk Địa Lí 6 – Cánh Diều
- Lý thuyết Địa Lí 6 – Cánh Diều
- Giải VBT Địa lí 6 – Cánh diều
- Giải sgk GDCD 6 – Cánh Diều
- Lý thuyết GDCD 6 – Cánh diều
- Giải sbt Giáo dục công dân 6 – Cánh diều
- Giải sgk Công nghệ 6 – Cánh Diều
- Lý thuyết Công nghệ 6 – Cánh Diều
- Giải sgk Khoa học tự nhiên 6 – Cánh Diều
- Giải sbt Khoa học tự nhiên 6 – Cánh Diều
- Lý thuyết Khoa học tự nhiên 6 – Cánh Diều
- Giải sgk Tin học 6 – Cánh Diều
- Lý thuyết Tin học 6 – Cánh Diều
- Giải sgk Tiếng Anh 6 - ilearn Smart World
- Ngữ pháp Tiếng Anh 6 i-learn Smart World
- Trọn bộ Từ vựng Tiếng Anh 6 ilearn Smart World đầy đủ nhất
- Giải sbt Tiếng Anh 6 - iLearn Smart World
- Bài tập Tiếng Anh 6 iLearn Smart World theo Unit có đáp án