Giải Toán 6 Bài tập cuối chương 2 (Cánh diều)

Giải Toán 6 Bài tập cuối chương 2

Bài tập

Giải Toán 6 trang 88 Tập 1

Toán lớp 6 trang 88 Bài 1: Sử dụng số nguyên âm để thể hiện các tình huống sau:

a) Nợ 150 nghìn đồng;

b) 600 m dưới mực nước biển;

c) 12 độ dưới 0 °C.

Lời giải:

a) Nợ 150 nghìn đồng có nghĩa là có – 150 nghìn đồng.

b) 600 m dưới mực nước biển có nghĩa là độ cao so với mực nước biển là – 600 m.

c) 12 độ dưới 0 °C có nghĩa nhiệt độ hiện tại ở đây là – 12 °C.

Toán lớp 6 trang 88 Bài 2: Trong Hình 10, hãy tính (theo mét):

a) Khoảng cách giữa rặng san hô và người thợ lặn;

b) Khoảng cách giữa người thợ lặn và mặt nước;

c) Khoảng cách giữa mặt nước và con chim;

d) Khoảng cách giữa rặng san hô và con chim.

Lời giải:

Quan sát Hình 10 trên trục mét, ta thấy:

+ Rặng san hô tương ứng với vị trí – 3 m

+ Người thợ lặn tương ứng với vị trí – 2 m

+ Mặt nước tương ứng với vị trí 0 m

+ Con chim tương ứng với vị trí 4 m

Do đó ta có:

a) Khoảng cách giữa rặng san hô và người thợ lặn là: (– 2) – (– 3) = 1 (m)

b) Khoảng cách giữa người thợ lặn và mặt nước là: 0 – (– 2) = 2 (m)

c) Khoảng cách giữa mặt nước và con chim là: 4 – 0 = 4 (m)

d) Khoảng cách giữa rặng san hô và con chim là: 4 – (– 3) = 7 (m).

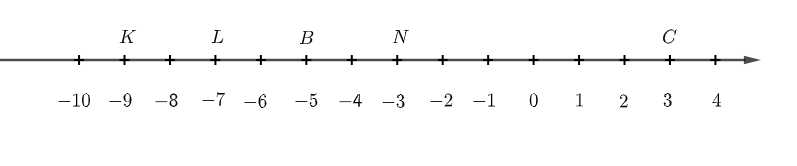
Toán lớp 6 trang 88 Bài 3: Quan sát trục số sau:

a) Các điểm N, B, C biểu diễn những số nào?

b) Điểm nào biểu diễn số – 7?

Lời giải:

Hoàn thành trục số đã cho ta được:

a) Khi đó ta có:

+ Điểm N biểu diễn số – 3

+ Điểm B biểu diễn số – 5

+ Điểm C biểu diễn số 3.

b) Điểm biểu diễn số – 7 là điểm L.

Toán lớp 6 trang 88 Bài 4: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai? Giải thích.

a) Kết quả của phép trừ số nguyên dương cho số nguyên dương là số nguyên dương.

b) Kết quả của phép trừ số nguyên dương cho số nguyên âm là số nguyên dương.

c) Kết quả của phép nhân số nguyên dương với số nguyên âm là số nguyên âm.

Lời giải:

a) Kết quả của phép trừ số nguyên dương cho số nguyên dương là số nguyên dương là phát biểu sai.

Ta có thể lấy ví dụ như sau:

Với hai số nguyên dương là 7 và 10 ta thực hiện phép trừ

7 – 10 = 7 + (– 10) = – 3 < 0

Ta được kết quả là – 3, đây là một số nguyên âm, không phải số nguyên dương.

b) Kết quả của phép trừ số nguyên dương cho số nguyên âm là số nguyên dương là phát biểu đúng.

Thật vậy, giả sử ta có số nguyên dương a bất kì đóng vai trò là số bị trừ và số nguyên âm – b đóng vai trò là số trừ. Khi đó ta thực hiện phép trừ:

a – (– b) = a + b

Vì – b là số nguyên âm, nên số đối của nó là b là một số nguyên dương

Do đó tổng a + b là một số nguyên dương, hay kết quả của phép trừ a – (– b) là một số nguyên dương.

c) Ta có tích hai số nguyên khác dấu là số nguyên âm.

Do đó kết quả của phép nhân số nguyên dương với số nguyên âm là số nguyên âm là phát biểu đúng.

Toán lớp 6 trang 88 Bài 5: Tính:

a) (– 15) . 4 – 240 : 6 + 36 : (– 2) . 3;

b) (– 2⁵) + [(– 69) : 3 + 53)] . (– 2) – 8.

Lời giải:

a) (– 15) . 4 – 240 : 6 + 36 : (– 2) . 3

= – (15 . 4) – 40 + [– (36 : 2) . 3]

= (– 60) – 40 + [(– 18) . 3]

= (– 60) – 40 + (– 54)

= (– 60) + (– 40) + (– 54)

= – (60 + 40 + 54)

= – 154.

b) (– 2⁵) + [(– 69) : 3 + 53] . (– 2) – 8

= (– 32) + [– (69 : 3) + 53] . (– 2) – 8

= (– 32) + [ (– 23) + 53] . (– 2) – 8

= (– 32) + (53 – 23) . (– 2) – 8

= (– 32) + 30 . (– 2) – 8

= (– 32) + (– 60) – 8

= – (32 + 60) – 8

= – 92 – 8

= – (92 + 8)

= – 100.

Toán lớp 6 trang 88 Bài 6: Tìm số nguyên x, biết:

a) 4 . x + 15 = – 5;

b) (– 270) : x – 20 = 70.

Lời giải:

a) 4 . x + 15 = – 5

4 . x = (– 5) – 15

4 . x = – 20

x = (– 20) : 4

x = – 5

Vậy x = – 5.

b) (– 270) : x – 20 = 70

(– 270) : x = 70 + 20

(– 270) : x = 90

x = (– 270) : 90

x = – 3

Vậy x = – 3.

Toán lớp 6 trang 88 Bài 7: Công ty An Bình có lợi nhuận ở mỗi tháng trong 4 tháng đầu năm là – 70 triệu đồng. Trong 8 tháng tiếp theo lợi nhuận mỗi tháng của công ty là 60 triệu đồng. Sau 12 tháng kinh doanh, lợi nhuận của công ty An Bình là bao nhiêu tiền?

Lời giải:

Cách 1.

Lợi nhuận của công ty An Bình trong 4 tháng đầu năm là:

– 70 . 4 = – 280 (triệu đồng)

Lợi nhuận của công ty An Bình trong 8 tháng tiếp theo là:

60 . 8 = 480 (triệu đồng)

Sau 12 tháng kinh doanh, lợi nhuận của công ty An Bình là:

(– 280) + 480 = 200 (triệu đồng)

Vậy sau 12 tháng kinh doanh, lợi nhuận của công ty An Bình là 200 triệu đồng.

Cách 2. (làm gộp)

Lợi nhuận của công ty An Bình sau 12 tháng kinh doanh là:

(– 70) . 4 + 60 . 8 = 200 (triệu đồng)

Vậy sau 12 tháng kinh doanh, lợi nhuận của công ty An Bình là 200 triệu đồng.

Toán lớp 6 trang 88 Bài 8: Người ta sử dụng biểu thức T = (I – E) : 12 để biểu diễn số tiền tiết kiệm trung bình mỗi tháng của một người, trong đó I là tổng thu nhập và E là tổng chi phí trong một năm của người đó. Bác Dũng có số tiền tiết kiệm trung bình mỗi tháng là 3 triệu đồng và tổng chi phí cả năm là 84 triệu đồng. Tính tổng thu nhập cả năm của bác Dũng.

Lời giải:

Bác Dũng có số tiền tiết kiệm trung bình mỗi tháng là 3 triệu đồng hay T = 3 triệu đồng.

Tổng chi phí cả năm của bác là 84 triệu đồng, hay E = 84 triệu đồng

Ta cần tìm tổng thu nhập I cả năm của bác Dũng.

Khi đó ta có biểu thức T = (I – E) : 12 với T = 3, E = 84

Thay T = 3 và E = 84 vào biểu thức trên ta được:

3 = (I – 84) : 12

Hay (I – 84) : 12 = 3

I – 84 = 3 . 12

I – 84 = 36

I = 36 + 84

I = 120.

Vậy tổng thu nhập cả năm của bác Dũng là 120 triệu đồng.

Lý thuyết Toán 6 Tổng hợp lý thuyết Chương 2 – Cánh diều

1. Số nguyên âm

+ Các số – 1, – 2, – 3, ... là các số nguyên âm. Số nguyên âm được nhận biết bằng dấu “–” ở trước số tự nhiên khác 0.

Ví dụ: – 5, – 10, – 10 000, ….

+ Cách đọc số nguyên âm: Có hai cách đọc số nguyên âm

Ví dụ: – 7 là số nguyên âm, đọc là âm bảy hoặc trừ bảy.

+ Số nguyên âm được sử dụng trong nhiều tình huống thực tiễn cuộc sống.

Chẳng hạn,

- Số nguyên âm được dùng để chỉ nhiệt độ dưới 0 °C

Ví dụ: Nhiệt độ 5 độ dưới 0 °C được viết là – 5 °C. đọc là: âm năm độ C.

- Số nguyên âm được dùng để chỉ độ cao dưới mực nước biển.

Ví dụ: Một thị trấn nhỏ gần thành phố Rốt-téc-đam (Rotterdam, Hà Lan) là một vùng đất trũng dưới mực nước biển xấp xỉ 7 m. Ta nói độ cao trung bình của vùng đất đó là – 7 m.

- Số nguyên âm được đùng để chỉ số tiền nợ, cũng như để chỉ số tiền lỗ trong kinh doanh.

Ví dụ: Khi ông Huy nợ 50 000 đồng thì ta có thể nói ông Huy có – 50 000 đồng.

Khi báo cáo kết quả kinh doanh, nếu bị lỗ 40 000 000 đồng thì ta có thể nói lợi nhuận là – 40 000 000 đồng.

- Số nguyên âm được dùng để chỉ thời gian trước Công nguyên.

Ví dụ: Nhà toán học Py-ta-go (Pythagoras) sinh năm – 570, nghĩa là ông sinh năm 570 trước Công nguyên.

2. Tập hợp $\mathbb{Z}$ các số nguyên

+ Số tự nhiên khác 0 còn được gọi là số nguyên dương.

+ Các số nguyên âm, số 0 và các số nguyên dương tạo thành tập hợp các số nguyên.

+ Tập hợp các số nguyên được kí hiệu là $\mathbb{Z}$.

Ví dụ:

+ Các số nguyên dương: 4, 6, 10 000, …

+ Tập hợp các số nguyên $\mathbb{Z}$= {…, – 2, – 1, 0, 1, 2, …}

Chú ý:

+ Số 0 không phải số nguyên âm, cũng không phải số nguyên dương.

+ Các số nguyên dương 1, 2, 3,... đều mang dấu “+" nên còn được viết là + 1, + 2, + 3,...

3. Biểu diễn số nguyên trên trục số

Ta có thể biểu diễn số nguyên trên trục số. Có hai loại trục số:

3.1 Trục số nằm ngang

Trên trục số nằm ngang, điểm biểu diễn số nguyên âm nằm bên trái điểm 0, điểm biểu diễn số nguyên dương nằm bên phải điểm 0.

3.2 Trục số thẳng đứng

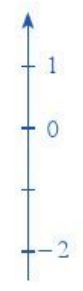
Trên trục số thẳng đứng, điểm biểu diễn số nguyên âm nằm phía dưới điểm 0, điểm biểu diễn số nguyên dương nằm phía trên điểm 0.

Chú ý: Khi nói “trục số” mà không nói gì thêm, ta hiểu là nói về trục số nằm ngang.

4. Số đối của một số nguyên

+ Trên trục số, hai số nguyên (phân biệt) có điểm biểu diễn nằm về hai phía của gốc 0 và cách đều gốc 0 được gọi là hai số đối nhau.

+ Số đối của 0 là 0.

Ví dụ:

– 4 và 4 là hai số đối nhau.

– 4 là số đối của 4 và 4 là số đối của – 4.

5. So sánh các số nguyên

5.1 So sánh hai số nguyên

+ Trên trục số nằm ngang, nếu điểm a nằm bên trái điểm b thì số nguyên a nhỏ hơn số nguyên b.

+ Trên trục số thẳng đứng, nếu điểm a nằm phía dưới điểm b thì số nguyên a nhỏ hơn số nguyên b.

+ Nếu a nhỏ hơn b thì ta viết là a < b hoặc b > a.

Ví dụ:

Điểm – 10 nằm bến trái điểm – 5 nên – 10 < – 5

Điểm 2 nằm bên phải điểm 0 nên 2 > 0.

Chú ý:

+ Số nguyên dương luôn lớn hơn 0. Số nguyên âm luôn nhỏ hơn 0.

+ Nếu a < b và b < c thì a < c

Ví dụ: – 2 < 0 và 0 < 5 thì – 2 < 5.

5.2 Cách so sánh hai số nguyên

5.2.1 So sánh hai số nguyên khác dấu

Số nguyên âm luôn nhỏ hơn số nguyên dương.

Ví dụ: – 7 là số nguyên âm và 5 là số nguyên dương nên – 7 < 5.

5.2.2 So sánh hai số nguyên cùng dấu

+ So sánh hai số nguyên dương: Đã biết ở chương I.

+ So sánh hai số nguyên âm:

Để so sánh hai số nguyên âm, ta làm như sau:

Bước 1. Bỏ dấu “–” trước cả hai số âm

Bước 2. Trong hai số nguyên dương nhận được, số nào nhỏ hơn thì số nguyên âm ban đầu (trước khi bỏ dấu “–”) sẽ lớn hơn.

Ví dụ: So sánh – 216 và – 309.

Bỏ dấu “–” trước các số – 216 và – 309, ta được các số lần lượt là 216 và 309.

Do 216 < 309 nên – 216 > – 309.

6. Phép cộng hai số nguyên cùng dấu

6.1 Phép cộng hai số nguyên dương

Cộng hai số nguyên dương chính là cộng hai số tự nhiên khác 0.

Ví dụ: 7 + 5 = 12

6.2 Phép cộng hai số nguyên âm

Để cộng hai số nguyên âm, ta làm như sau:

Bước 1. Bỏ đấu “–” trước mỗi số

Bước 2. Tính tổng của hai số nguyên dương nhận được ở Bước 1

Bước 3. Thêm dấu “–” trước kết quả nhận được ở Bước 2, ta có tổng cần tìm.

Ví dụ: (– 80) + (– 6) = – (80 + 6) = – 86

Chú ý:

+ Tổng của hai số nguyên dương là số nguyên dương.

+ Tổng của hai số nguyên âm là số nguyên âm.

7. Phép cộng hai số nguyên khác dấu

Để cộng hai số nguyên khác dấu, ta làm như sau:

Bước 1. Bỏ dấu “–” trước số nguyên âm, giữ nguyên số còn lại

Bước 2. Trong hai số nguyên dương nhận được ở Bước 1, ta lấy số lớn hơn trừ đi số nhỏ hơn

Bước 3. Cho hiệu vừa nhận được dấu ban đầu của số lớn hơn ở Bước 2, ta có tổng cần tìm.

Ví dụ: (– 6) + 3 = – (6 – 3) = – 3

Chú ý: Hai số nguyên đối nhau có tổng bằng 0.

Chẳng hạn, – 7 và 7 là hai số nguyên đối nhau, ta có: (– 7) + 7 = 0.

8. Tính chất của phép cộng các số nguyên

Phép cộng các số nguyên có các tính chất sau:

+ Giao hoán: a + b = b + a;

+ Kết hợp: (a + b) + c = a + ( b + c);

+ Cộng với số 0: a + 0 = 0 + a = a;

+ Cộng với số đối: a + (– a) = (– a) + a = 0.

Ví dụ: Tính: a) 51 + (– 97) + 49; b) 65 + (– 42) + (– 65).

Lời giải:

a) 51 + (– 97) + 49

= 51 + 49 + (– 97) (tính chất giao hoán)

= (51 + 49) + (– 97) (tính chất kết hợp)

= 100 + (– 97)

= 100 – 97

= 3.

b) 65 + (– 42) + (– 65)

= 65 + (– 65) + (– 42) (tính chất giao hoán)

= [65 + (– 65)] + (– 42) (tính chất kết hợp)

= 0 + (– 42) (cộng với số đối)

= – 42. (cộng với số 0)

9. Phép trừ số nguyên

Muốn trừ số nguyên a cho số nguyên b, ta cộng a với số đối của b:

a – b = a + (– b).

Chú ý: Phép trừ trong $\mathbb{N}$ không phải bao giờ cũng thực hiện được, còn phép trừ trong $\mathbb{Z}$ luôn thực hiện được.

Ví dụ: (– 10) – 15 = (– 10) + (– 15) = – (10 + 15) = – 25

6 – 18 = 6 + (– 18) = – (18 – 6) = – 12

10. Quy tắc dấu ngoặc

• Khi bỏ dấu ngoặc có dấu “+” đằng trước thì giữ nguyên dấu của các số hạng trong ngoặc.

a + (b + c) = a + b + c

a + (b – c) = a + b – c.

• Khi bỏ dấu ngoặc có dấu “–” đằng trước, ta phải đổi dấu của các số hạng trong ngoặc: dấu “+” thành dấu “–” và dấu “–” thành dấu “+”.

a – (b + c) = a – b – c

a – (b – c) = a – b + c.

Ví dụ: Tính (– 147) – (13 – 47).

Ta có:

(– 147) – (13 – 47)

= (– 147) – 13 + 47 (quy tắc dấu ngoặc)

= (– 147) + 47 – 13 (tính chất giao hoán)

= [(– 147) + 47] – 13 (tính chất kết hợp)

= [– (147 – 47)] – 13

= (– 100) – 13

= (– 100) + (– 13)

= – (100 + 13)

= – 113.

11. Phép nhân hai số nguyên khác dấu

Để nhân hai số nguyên khác dấu, ta làm như sau:

Bước 1. Bỏ dấu “–” trước số nguyên âm, giữ nguyên số nguyên còn lại

Bước 2. Tính tích của hai số nguyên dương nhận được ở Bước 1

Bước 3. Thêm dấu “–” trước kết quả nhận được ở Bước 2, ta có tích cần tìm.

Chú ý: Tích của hai số nguyên khác dấu là số nguyên âm.

Ví dụ: (– 6) . 7 = – (6 . 7) = – 42

20 . (– 10) = – (20 . 10) = – 200

12. Phép nhân hai số nguyên cùng dấu

12.1 Phép nhân hai số nguyên dương

Nhân hai số nguyên dương chính là nhân hai số tự nhiên khác 0.

Ví dụ: 4 . 6 = 24; 16 . 2 = 32.

12.2 Phép nhân hai số nguyên âm

Để nhân hai số nguyên âm, ta làm như sau:

Bước 1. Bỏ dấu “–” trước mỗi số

Bước 2. Tính tích của hai số nguyên dương nhận được ở Bước 1, ta có tích cần tìm.

Chú ý: Tích của hai số nguyên cùng dấu là số nguyên dương.

Ví dụ: (– 5) . (– 9) = 5 . 9 = 45

(– 20) . (– 6) = 20 . 6 = 120

Chú ý: Cách nhận biết dấu của tích

(+) . (+) → (+)

(–) . (–) → (+)

(+) . (–) → (–)

(–) . (+) → (–)

13. Tính chất của phép nhân các số nguyên

Giống như phép nhân các số tự nhiên, phép nhân các số nguyên cũng có các tính chất: giao hoán; kết hợp; nhân với số 1; phân phối của phép nhân đối với phép cộng, phép trừ.

+ Tính chất giao hoán: a . b = b . a

+ Tính chất kết hợp: (a . b) . c = a . (b . c)

+ Tính chất nhân với số 1: a . 1 = 1 . a = a

+ Tính chất phân phối của phép nhân đối với phép cộng: a . (b + c) = a . b + a . c

Tính chất phân phối của phép nhân đối với phép trừ: a . (b – c) = a . b – a . c

Chú ý:

a . 0 = 0 . a = 0

a . b = 0 thì hoặc a = 0 hoặc b = 0

Ví dụ: Tính

a) (– 9) . 4 . (– 5);

b) (– 127 086) . 674 . 0;

c) (– 4) . 7 + (– 4) . 3.

Lời giải:

a) (– 9) . 4 . (– 5) = (– 9) . [4 . (– 5)] = (– 9) . (– 20) = 9 . 20 = 180

b) (– 127 086) . 674 . 0 = 0

c) (– 4) . 7 + (– 4) . 3 = (– 4) . (7 + 3) = (– 4) . 10 = – 40

14. Phép chia hết hai số nguyên khác dấu

Để chia hai số nguyên khác dấu, ta làm như sau:

Bước 1. Bỏ dấu “–” trước số nguyên âm, giữ nguyên số còn lại

Bước 2. Tính thương của hai số nguyên dương nhận được ở Bước 1

Bước 3. Thêm dấu “–” trước kết quả nhận được ở Bước 2, ta có thương cần tìm.

Ví dụ: (– 24) : 4 = – (24 : 4) = – 6

45 : (– 9) = – (45 : 9) = – 5

15. Phép chia hết hai số nguyên cùng dấu

15.1 Phép chia hết hai số nguyên dương

Phép chia hết của một số nguyên dương cho một số nguyên dương là phép chia hết hai số tự nhiên với số chia khác 0.

Ví dụ: 32 : 8 = 4; 10 : 2 = 5; …

15.2 Phép chia hết hai số nguyên âm

Để chia hai số nguyên âm, ta làm như sau:

Bước 1. Bỏ dấu “–” trước mỗi số

Bước 2. Tính thương của hai số nguyên dương nhận được ở Bước 1, ta có thương cần tìm.

Ví dụ: (– 12) : (– 3) = 12 : 3 = 4

(– 100) : (– 20) = 100 : 20 = 5

Chú ý:

• Cách nhận biết dấu của thương:

(+) : (+) → (+)

(–) : (–) → (+)

(+) : (–) → (–)

(–) : (+) → (–)

• Thứ tự thực hiện các phép tính với số nguyên (trong biểu thức không chứa dấu ngoặc hoặc có chứa dấu ngoặc) cũng giống như thứ tự thực hiện các phép tính với số tự nhiên.

16. Quan hệ chia hết

Cho hai số nguyên a, b với . Nếu có số nguyên q sao cho a = b . q thì ta nói:

• a chia hết cho b;

• a là bội của b;

• b là ước của a.

Ví dụ: Ta có: – 48 = 6 . (– 8) nên – 48 chia hết cho 6 hay – 48 là bội của 6 và 6 là ước của – 48.

Chú ý:

+ Nếu a là bội của b thì – a cũng là bội của b.

+ Nếu b là ước của a thì – b cũng là ước của a.

Ví dụ: 6 chia hết cho 2 nên 6 là bội của 2, do đó – 6 cũng là bội của 2

– 25 chia hết cho 5 nên 5 là ước của – 25, do đó – 5 cũng là ước của – 25.

Xem thêm lời giải bài tập Toán lớp 6 sách Cánh diều hay, chi tiết khác: