Giải Toán 6 Bài tập cuối chương 3 (Cánh diều)

Giải Toán 6 Bài tập cuối chương 3

Bài tập

Giải Toán 6 trang 117 Tập 1

Toán lớp 6 trang 117 Bài 1: Tạo ra hình hộp có nắp

Hãy vẽ các hình chữ nhật trên một miếng bìa (mỏng) theo cách như ở Hình 96, sau đó cắt, gấp lại và dán mép để tạo ra hình hộp có nắp.

Lời giải:

- Chuẩn bị giấy mỏng có ô vuông, vẽ theo mẫu Hình 69

- Cắt phần đã vẽ theo một đường

- Cách gấp: gấp dựng đứng các hình chữ nhật nhỏ gắn với phần hình chữ nhật to thứ nhất, gấp phần hình chữ nhật thứ hai lên tạo thành nắp sau đó dán các mép gấp, ta được hình hộp có nắp.

Toán lớp 6 trang 117 Bài 2: Cho các hình sau đây:

(1) Đoạn thẳng AB.

(2) Tam giác đều ABC.

(3) Hình tròn tâm O.

(4) Hình thang cân ABCD (có đáy lớn CD)

(5) Hình thoi ABCD.

Trong các hình nói trên:

a) Hình nào có trục đối xứng? Chỉ ra trục đối xứng của hình đó.

b) Hình nào có tâm đối xứng? Chỉ ra tâm đối xứng của hình đó.

Lời giải:

a) Cả 5 hình đã cho đều có trục đối xứng như sau:

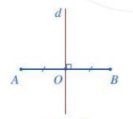
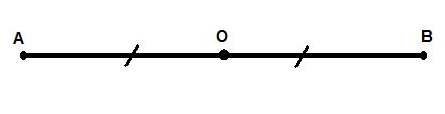
(1) Đoạn thẳng AB là hình có 1 trục đối xứng và trục đối xứng là đường thẳng d đi qua trung điểm O của đoạn thẳng AB và vuông góc với AB.

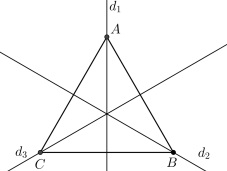
(2) Tam giác đều ABC là hình có trục đối xứng và có 3 trục đối xứng d₁, d₂, d₃ như sau:

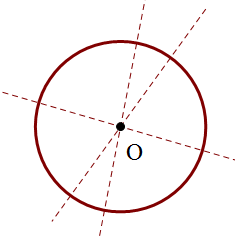
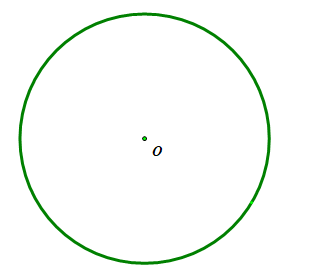
(3) Hình tròn tâm O có vô số trục đối xứng và mỗi trục đối xứng là một đường thẳng đi qua tâm O của nó.

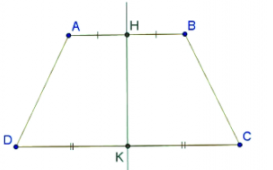
(4) Hình thang cân ABCD (có đáy lớn CD) là hình có 1 trục đối xứng và trục đối xứng là đường thẳng đi qua trung điểm H và K của 2 đáy AB và CD:

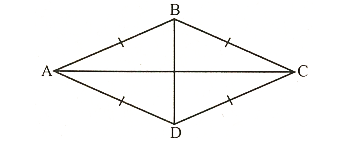
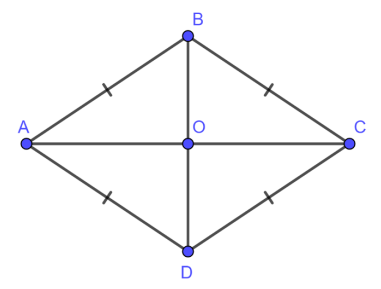
(5) Hình thoi ABCD có 2 trục đối xứng là hai đường chéo AC và BD

b) Trong 5 hình đã cho: đoạn thẳng AB, hình tròn tâm O, hình thoi ABCD là các hình có tâm đối xứng. Các hình tam giác đều ABC, hình thang cân ABCD là hình không có tâm đối xứng.

(1) Đoạn thẳng AB là hình có tâm đối xứng và tâm đối xứng là trung điểm O của AB

(3) Hình tròn tâm O có tâm đối xứng chính là tâm O

(5) Hình thoi ABCD có tâm đối xứng là giao điểm O của hai đường chéo AC và BD

Toán lớp 6 trang 117 Bài 3: Hãy quan sát xung quanh và chỉ ra những hình:

a) Có trục đối xứng.

b) Có tâm đối xứng

c) Vừa có trục đối xứng vừa có tâm đối xứng.

Lời giải:

a) Một số hình có trục đối xứng:

+) Hoa văn trang trí trên gạch hoa

+) Hình mặt cười

+) Hình con bướm

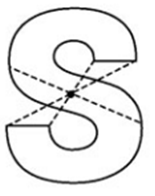
b) Một số hình có tâm đối xứng:

+) Hình biển báo giao thông

+) Hình chữ S

+) Hình chữ Z

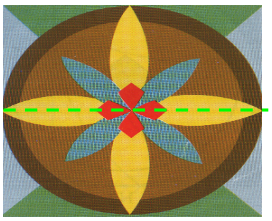
c) Một số hình vừa có tâm đối xứng vừa có trục đối xứng

+) Hình trang trí bông hoa

+) Lục giác đều

+) Hình vuông

Toán lớp 6 trang 117 Bài 4: Hãy tìm và kể ra một số ứng dụng của tính đối xứng trong thực tiễn mà em biết.

Lời giải:

Một số ứng dụng của tính đối xứng trong thực tiễn:

+) Làm hình trang trí nghệ thuật

+) Thiết các các công trình kiến trúc

Nhà thờ Mosque (nhà thờ Hồi Giáo) tại Abu Dhabi.

Tháp Phước Duyên ở chùa Thiên Mụ (Huế)

Toán lớp 6 trang 117 Bài 5:

a) Một hình thoi có cạnh 4 cm thì chu vi của nó bằng bao nhiêu?

b) Một hình vuông có chu vi là 40 cm thì cạnh của nó bằng bao nhiêu?

c) Một hình chữ nhật có chu vi 30 cm và chiều rộng là 7 cm thì chiều dài của nó bằng bao nhiêu?

d) Một hình chữ nhật có chu vi 36 cm và chiều dài gấp đôi chiều rộng thì mỗi cạnh của nó bằng bao nhiêu?

Lời giải:

Để làm bài tập này, ta cần nhớ cách tính chu vi của các hình: hình thoi, hình vuông, hình chữ nhật (xem kiến thức ở các bài học).

a) Chu vi hình thoi có cạnh 4 cm là: 4 . 4 = 16 (cm)

b) Hình vuông có chu vi 40 cm thì có độ dài cạnh là: 40 : 4 = 10 (cm)

c) Một hình chữ nhật có chu vi 30 cm và chiều rộng là 7 cm.

Nửa chu vi của hình chữ nhật là: 30 : 2 = 15 (cm)

Chiều dài của hình chữ nhật là: 15 – 7 = 8 (cm)

d) Nửa chu vi hình chữ nhật là: 36 : 2 = 18 (cm)

Chiều dài gấp đôi chiều rộng, hay chiều rộng bằng $\frac{1}{2}$chiều dài, khi đó ta có sơ đồ:

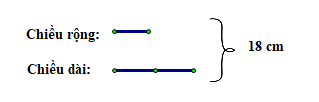
Tổng số phần bằng nhau là: 1 + 2 = 3 (phần)

Giá trị một phần hay chiều rộng là: 18 : 3 = 6 (cm)

Chiều dài là: 6 . 2 = 12 (cm)

Vậy chiều dài và chiều rộng của hình chữ nhật lần lượt là 12 cm và 6 cm.

Toán lớp 6 trang 117 Bài 6: Sử dụng thước, hãy đo và cho biết chu vi của một số đồ vật có dạng hình chữ nhật trong thực tiễn. Chẳng hạn: đo chu vi mặt bàn học của em; đo chu vi bìa một quyển sách mà em có; …

Lời giải:

Em tự đo chiều dài và chiều rộng của các vật có dạng hình chữ nhật rồi áp dụng công thức tính chu vi hình chữ nhật để biết được chu vi các vật cần đo.

Giải Toán 6 trang 118 Tập 1

Toán lớp 6 trang 118 Bài 7: Quan sát Hình 97, Hình 98 và tính diện tích của phần tô xanh ở mỗi hình đó.

Lời giải:

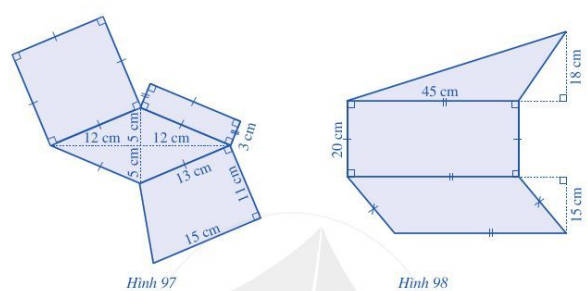
+) Trong Hình 97

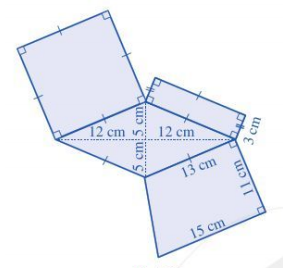
Ta chia phần tô màu xanh thành các hình: hình vuông có cạnh 13 cm; hình chữ nhật có chiều dài 13 cm, chiều rộng 3 cm; hình thoi có độ dài hai đường chéo lần lượt là 12 + 12 = 24 cm, 5 + 5 = 10 cm và hình thang có đáy lớn 15 cm, đáy bé 13 cm và chiều cao 11 cm. Diện tích phần tô màu xanh chính là tổng diện tích của các hình trên.

Diện tích hình vuông là: 13 . 13 = 169 (cm²)

Diện tích hình chữ nhật là: 13 . 3 = 39 (cm²)

Diện tích hình thang là: $\frac{(13+15).11}{2}$ (cm²)

Hình thoi có diện tích là: $\frac{24.10}{2}$ (cm²)

Tổng diện tích phần màu xanh trên Hình 97 là:

169 + 39 + 154 + 120 = 482 (cm²)

Vậy phần màu xanh trong Hình 97 có diện tích là 482 cm².

+) Trong Hình 98:

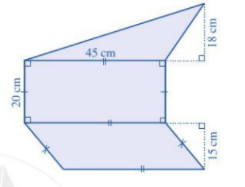
Ta chia phần màu xanh thành các hình: một hình tam giác có chiều cao là 18 cm ứng với cạnh đáy là 45 cm; một hình chữ nhật có chiều dài 45 cm, chiều rộng 20 cm và một hình bình hành có độ dài đường cao là 15 cm ứng với đáy là 45 cm. Diện tích phần tô màu xanh chính là tổng diện tích của các hình trên.

Diện tích hình tam giác là: 45 . 18 : 2 = 405 (cm²)

Diện tích hình chữ nhật là: 45 . 20 = 900 (cm²)

Diện tích hình bình hành là: 45 . 15 = 675 (cm²)

Tổng diện tích các hình là: 405 + 900 + 675 = 1 980 (cm²)

Vậy phần tô màu xanh trong Hình 98 có diện tích là 1 980 cm².

Toán lớp 6 trang 118 Bài 8: Trên mảnh đất có dạng hình chữ nhật với chiều dài là 28 m và chiều rộng là 24 m, người ta định xây dựng một vườn hoa hình chữ nhật và bớt ra một phần đường đi như ở Hình 99.

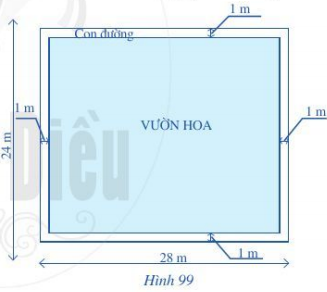
a) Tính diện tích mảnh đất có dạng hình chữ nhật đó.

b) Tính diện tích vườn hoa.

c) Người ta định dùng những viên gạch chống trượt có dạng hình vuông có cạnh là 50 cm để lát đường đi. Cần dùng bao nhiêu viên gạch như thế? Biết rằng diện tích các mối nối và sự hao hụt là không đáng kể.

d) Người ta làm hàng rào xung quanh vườn hoa. Tính chiều dài hàng rào đó.

Lời giải:

a) Diện tích mảnh đất hình chữ nhật là:

28 . 24 = 672 (m²)

b) Quan sát hình 99, ta thấy sau khi bớt ra một phần đường đi thì phần vườn trồng hoa có dạng hình chữ nhật với:

Chiều dài phần vườn trồng hoa là: 28 – 1 – 1 = 26 (m)

Chiều rộng phần vườn trồng hoa là: 24 – 1 – 1 = 22 (m)

Diện tích phần vườn hoa là:

26 . 22 = 572 (m²)

c) Diện tích phần đường đi chính là hiệu diện tích mảnh đất với diện tích phần vườn hoa. Do đó diện tích phần đường đi là:

672 – 572 = 100 (m²)

Đổi 100 m² = 1 000 000 cm²

Một viên gạch hình vuông có diện tích là:

50 . 50 = 2 500 (cm²)

Cần dùng số viên gạch là:

1 000 000 : 2 500 = 400 (viên gạch)

d) Phần chiều dài hàng rào xung quanh vườn hoa chính là chu vi phần vườn hoa có dạng hình chữ nhật

Vậy chiều dài hàng rào là: (22 + 26) . 2 = 96 m.

Toán lớp 6 trang 118 Bài 9: Bạn Thảo muốn cắt miếng bìa màu xanh có diện tích là 28 cm² như Hình 100. Biết chu vi hình vuông ABCD là 16 cm. Tính giúp bạn Thảo độ dài cạnh EG.

Lời giải:

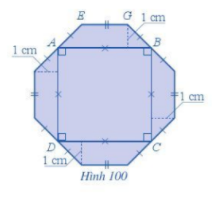
Miếng bìa màu xanh như Hình 100 được tạo bởi 1 hình vuông ABCD có chu vi là 16 cm và 4 phần bìa bằng nhau có dạng hình thang cân như hình ABGE.

Độ dài cạnh của hình vuông ABCD là: 16 : 4 = 4 (cm)

Hay AB = 4 cm

Diện tích hình vuông ABCD là: 4 . 4 = 16 (cm²)

Diện tích phần còn lại (cả mảnh bìa trừ đi phần hình vuông ABCD) là:

28 – 16 = 12 (cm)

Diện tích phần còn lại của miếng bìa là tổng diện tích của 4 hình thang cân.

Do đó diện tích hình thang cân ABGE là: 12 : 4 = 3 (cm²)

Hình thang cân ABGE có diện tích 3 cm² và có đáy AB = 4 cm, chiều cao 1 cm

Khi đó ta có: $\frac{(\mathrm{AB}\hspace{0.17em}+ \mathrm{EG}).1}{2}=3$ hay $\frac{(4 + \mathrm{EG}).1}{2}=3$

Suy ra: EG = 3 . 2 : 1 – 4 = 2 (cm)

Vậy độ dài cạnh EG là 2 cm.

Lý thuyết Toán 6 Tổng hợp lý thuyết Chương 3 – Cánh diều

1. Tam giác đều

1.1 Nhận biết tam giác đều

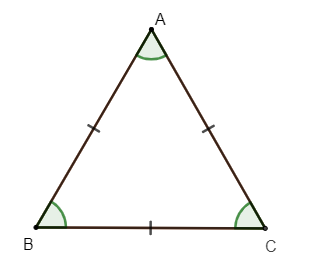
Tam giác đều ABC có

+ Ba cạnh bằng nhau: AB = BC = CA

+ Ba góc ở các đỉnh A, B, C bằng nhau.

Chú ý: Trong hình học nói chung, tam giác nói riêng, các cạnh bằng nhau (hay các góc bằng nhau) thường được chỉ rõ ràng bằng cùng một ký hiệu (xem hình vẽ trên).

1.2 Vẽ tam giác đều

Vẽ tam giác đều bằng thước và compa khi biết độ dài cạnh.

Ví dụ: Dùng thước và compa vẽ tam giác đều ABC có độ dài cạnh bằng 3 cm.

Lời giải:

Để vẽ tam giác đều ABC có độ dài cạnh bằng 3 cm, ta làm như sau:

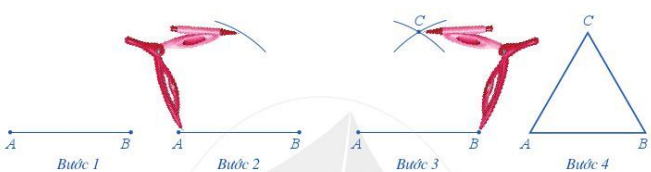
Bước 1. Dùng thước vẽ đoạn thẳng AB = 3 cm

Bước 2. Lấy A làm tâm, dùng compa vẽ một phần đường tròn có bán kính AB.

Bước 3. Lấy B làm tâm, dùng compa vẽ một phần đường tròn có bán kính BA; gọi C là giao điểm của hai phần đường tròn vừa vẽ.

Bước 4. Dùng thước vẽ các đoạn thẳng AC và BC

Khi đó ta được tam giác đều ABC có cạnh bằng 3 cm.

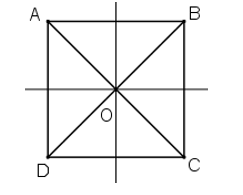
2. Hình vuông

2.1 Nhận biết hình vuông

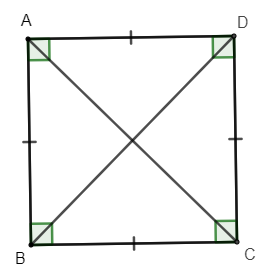
Hình vuông ABCD có:

+ Bốn cạnh bằng nhau: AB = BC = CD = DA

+ Hai cạnh đối AB và CD; AD và BC song song với nhau.

+ Hai đường chéo bằng nhau: AC = BD

+ Bốn góc ở các đỉnh A, B, C, D là góc vuông.

2.2 Vẽ hình vuông

Dùng ê ke vẽ hình vuông khi biết độ dài cạnh.

Ví dụ: Vẽ bằng ê ke hình vuông ABCD, biết độ dài cạnh bằng 7 cm.

Lời giải:

Để vẽ hình vuông ABCD, ta làm như sau:

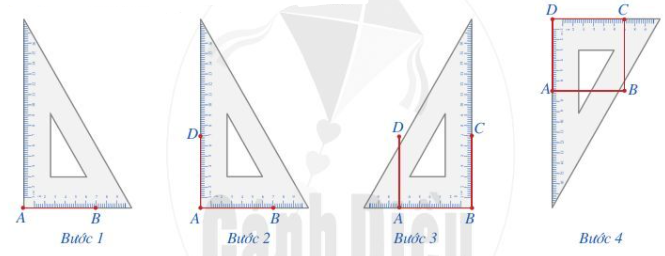
Bước 1. Vẽ theo một cạnh góc vuông của ê ke đoạn thẳng AB = 7 cm.

Bước 2. Đặt đỉnh góc vuông của ê ke trùng với điểm A và một cạnh ê ke bằm trên AB, vẽ theo cạnh kia của ê ke đoạn thẳng AD = 7cm.

Bước 3. Xoay ê ke rồi thực hiện tương tự như ở Bước 2 để được cạnh BC = 7 cm.

Bước 4. Vẽ đoạn thẳng CD.

2.3 Chu vi và diện tích của hình vuông

Hình vuông có độ dài cạnh bằng a có:

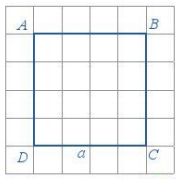
+ Chu vi của hình vuông là C = 4a

+ Diện tích của hình vuông là S = a . a = a²

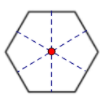
3. Lục giác đều

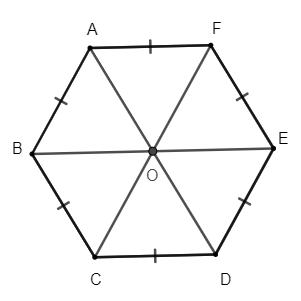
Lục giác đều ABCDEF có:

+ Sáu cạnh bằng nhau: AB = BC = CD = DE = EF = FA

+ Ba đường chéo chính cắt nhau tại điểm O.

Ba đường chéo chính bằng nhau: AD = BE = CF

+ Sáu góc ở các đỉnh A, B, C, D, E, F bằng nhau.

4. Hình chữ nhật

4.1 Nhận biết hình chữ nhật

Cho hình chữ nhật ABCD:

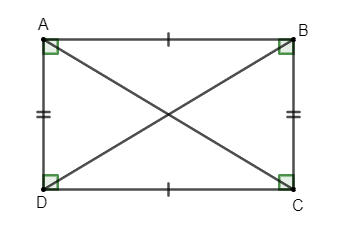
Khi đó hình chữ nhật ABCD có:

+ Hai cạnh đối bằng nhau: AB = CD; AD = BC;

+ Hai cạnh đối AB và CD; AD và BC song song với nhau;

+ Hai đường chéo bằng nhau: AC = BD;

+ Bốn góc ở các đỉnh A, B, C, D đều là góc vuông.

4.2 Vẽ hình chữ nhật

Ta sử dụng ê ke để vẽ hình chữ nhật khi biết độ dài hai cạnh của nó:

Chẳng hạn, vẽ hình chữ nhật ABCD biết AB = 6 cm, AD = 9 cm.

Ta thực hiện các bước như sau:

Bước 1. Vẽ theo một cạnh góc vuông của ê ke đoạn thẳng AB = 6 cm.

Bước 2. Đặt đỉnh góc vuông của ê ke trùng với điểm A và một cạnh ê ke nằm trên AB, vẽ theo cạnh kia của ê ke đoạn thẳng AD = 9 cm.

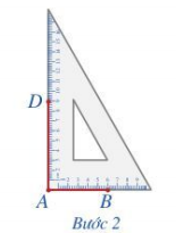
Bước 3. Xoay ê ke rồi thực hiện tương tự như ở Bước 2 để được cạnh BC = 9 cm.

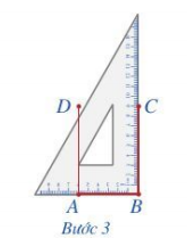
Bước 4. Vẽ đoạn thẳng CD.

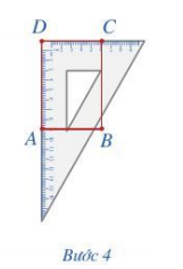
Vậy ta có hình chữ nhật ABCD thỏa mãn yêu cầu bài toán.

4.3 Chu vi và diện tích hình chữ nhật

Hình chữ có độ dài hai cạnh là a và b, ta có:

- Chu vi của hình chữ nhật là: C = 2(a + b);

- Diện tích của hình chữ nhật là: S = a . b.

5. Hình thoi

5.1 Nhận biết hình thoi

Cho hình thoi ABCD, có hai đường chéo AC và BD cắt nhau tại O.

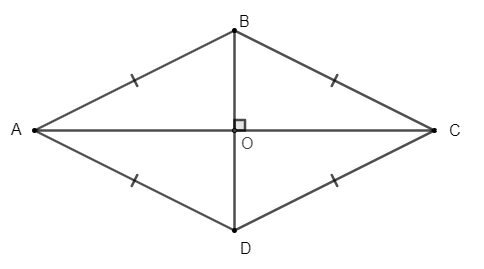
Khi đó, hình thoi ABCD có:

+ Bốn cạnh bằng nhau: AB = BC = CD = DA;

+ Hai cạnh đối AB và CD, AD và BC song song với nhau;

+ Hai đường chéo AC và BD vuông góc với nhau.

5.2 Vẽ hình thoi

Ta có thể vẽ được hình thoi khi biết độ dài một cạnh và độ dài một đường chéo bằng thước kẻ và compa.

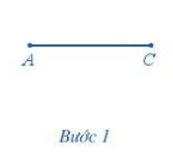
Chẳng hạn, vẽ hình thoi ABCD biết AB = 5 cm và AC = 8 cm.

Để vẽ hình thoi ABCD, ta làm như sau:

Bước 1. Dùng thước vẽ đoạn thẳng AC = 8 cm

Bước 2. Dùng compa vẽ một phần đường tròn tâm A bán kính 5 cm

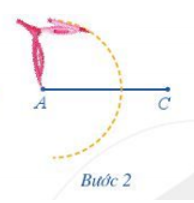
Bước 3. Dùng compa vẽ một phần đường tròn tâm C bán kính 5 cm; phần đường tròn này cắt phần đường tròn tâm A vẽ ở Bước 2 tại các điểm B và D

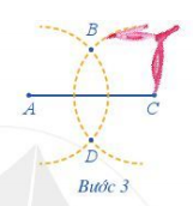
Bước 4. Dùng thước vẽ các đoạn thẳng AB, BC, CD, DA.

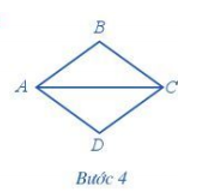
Vậy ta được hình thoi ABCD thỏa mãn yêu cầu.

5.3 Chu vi và diện tích hình thoi

Cho hình thoi có độ dài cạnh là a và độ dài hai đường chéo là m và n, ta có:

- Chu vi của hình thoi là C = 4a;

- Diện tích của hình thoi là S = $\frac{1}{2}$ . m . n.

6. Hình bình hành

6.1 Nhận biết hình bình hành

Cho hình bình hành ABCD

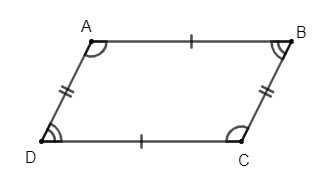
Khi đó hình bình hành ABCD có:

+ Hai cạnh đối AB và CD, BC và AD song song với nhau;

+ Hai cạnh đối bằng nhau: AB = CD; BC = AD;

+ Hai góc ở các đỉnh A và C bằng nhau; hai góc ở các đỉnh B và D bằng nhau.

6.2 Vẽ hình bình hành

Ta có thể vẽ hình bình hành bằng thước và compa.

Chẳng hạn, vẽ hình bình hành ABCD nhận hai đoạn thẳng AB, AD làm cạnh.

Để vẽ hình bình hành ABCD ta thực hiện các bước sau:

Bước 1. Lấy B làm tâm, dùng compa vẽ một phần đường tròn có bán kính AD. Lấy D làm tâm, dùng compa vẽ một phần đường tròn có bán kính AB. Gọi C là giao điểm của hai phần đường tròn này.

Bước 2. Dùng thước vẽ các đoạn thẳng BC và CD.

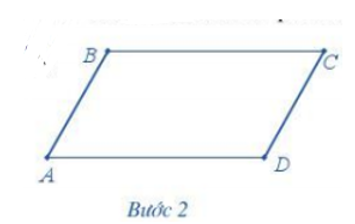
Ta được hình bình hành ABCD.

6.3 Chu vi và diện tích của hình bình hành

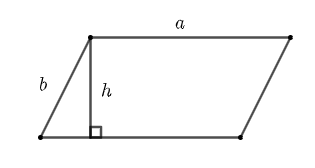
Hình bình hành có độ dài hai cạnh là a và b, độ dài đường cao ứng với cạnh a là h, ta có:

- Chu vi của hình bình hành là C = 2(a + b);

- Diện tích của hình bình hành là S = a . h.

7. Hình thang cân

7.1 Nhận biết hình thang cân

Cho hình thang cân ABCD

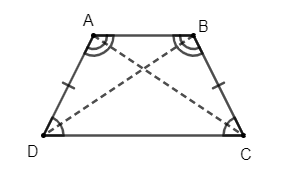
Khi đó hình thang cân ABCD có:

+ Hai cạnh đáy AB và CD song song với nhau;

+ Hai cạnh bên bằng nhau: AD = BC; hai đường chéo bằng nhau: AC = BD;

+ Hai góc kề với đáy AB bằng nhau, tức là hai góc DAB và CBA bằng nhau; hai góc kề với đáy CD bằng nhau, tức là hai góc ADC và góc BCD bằng nhau.

7.2 Chu vi và diện tích hình thang cân

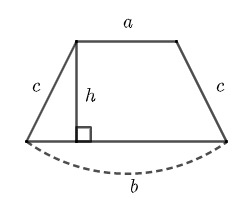
(Hình thang cân có hai cạnh bên bằng nhau)

- Chu vi của hình thang cân bằng tổng độ dài các cạnh của hình thang cân đó

C = a + b + c + c = a + b + 2c

- Diện tích của hình thang cân bằng tổng độ dài hai cạnh đáy nhân với chiều cao rồi chia đôi

$S=\frac{\left(a+b\right).h}{2}$.

8. Hình có trục đối xứng

Quan sát các hình sau:

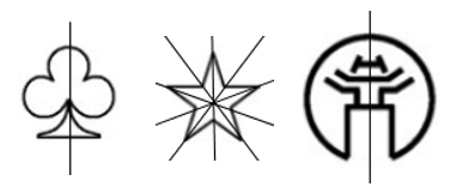
Các hình trên có đặc điểm chung là khi chia mỗi hình thành hai nửa và gấp theo mép đường thẳng ở giữa hình thì hai nửa này sẽ trùng khít vào nhau.

Cụ thể, trong hình dưới đây:

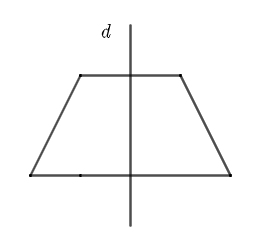
Đường thẳng d chia hình thành hai nửa, nếu ta gấp theo đường thẳng d thì hai nửa này sẽ trùng khít vào nhau.

Những hình như vậy gọi là hình có trục đối xứng và đường thẳng d được gọi là trục đối xứng của hình.

Chú ý: Hình có trục đối xứng còn được gọi là hình đối xứng trục.

9. Trục đối xứng của một số hình

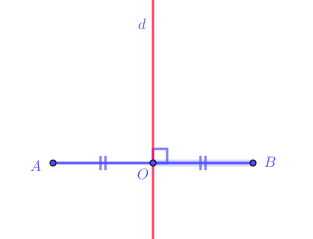
9.1

Đoạn thẳng AB là hình có trục đối xứng và trục đối xứng là đường thẳng d đi qua trung điểm O của đoạn thẳng AB và vuông góc với AB.

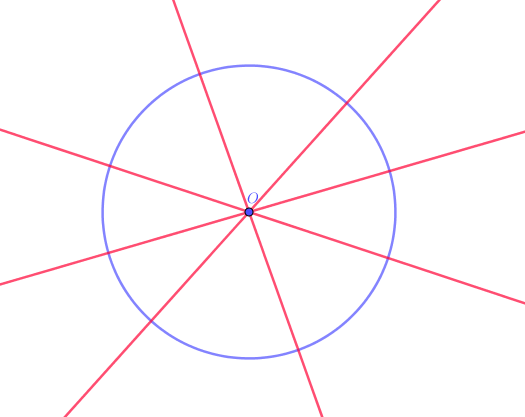
9.2

Đường tròn là hình có nhiều trục đối xứng và mỗi trục đối xứng là một đường thẳng đi qua tâm của nó.

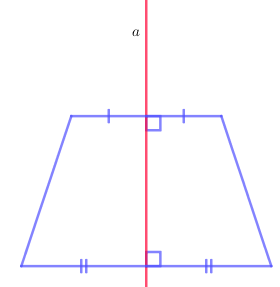
9.3 Hình thang cân có một trục đối xứng là đường thẳng a đi qua điểm chính giữa của hai đáy.

9.4 Hình lục giác đều có 6 trục đối xứng là các đường thẳng m, n, p, q, r, s (như hình dưới

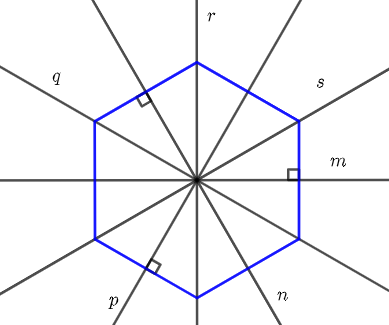
Chú ý: Không phải hình nào cũng đều có trục đối xứng.

10. Hình có tâm đối xứng

10.1 Cho đường tròn tâm O, đường kính AB.

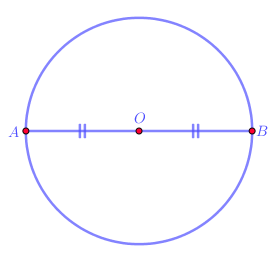
+ Vì O là trung điểm của đoạn thẳng AB nên ta nói hai điểm A và B đối xứng với nhau qua tâm O.

+ Đường tròn tâm O là hình có tâm đối xứng, tâm đối xứng chính là tâm O của đường tròn.

10.2 Lấy bốn chiếc ê ke giống nhau để xếp thành hình. Ta được một hình mới là hình có tâm đối xứng và điểm O được gọi là tâm đối xứng của hình.

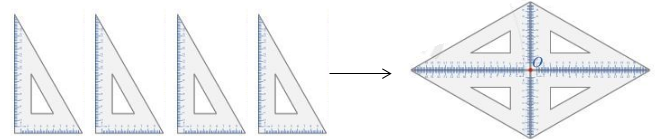
Chú ý: Hình có tâm đối xứng còn được gọi là hình đối xứng tâm.

11. Tâm đối xứng của một số hình

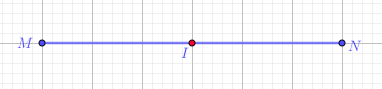
11.1 Đoạn thẳng MN là hình có tâm đối xứng và tâm đối xứng là trung điểm I của đoạn thẳng đó.

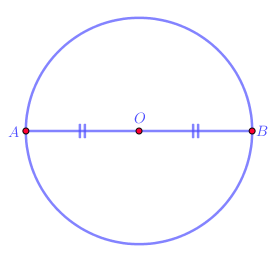
11.2 Hình tròn là hình có tâm đối xứng và tâm đối xứng là tâm của nó.

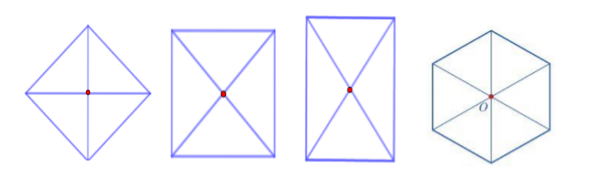
11.3 Hình thoi, hình vuông, hình chữ nhật, hình lục giác đều có tâm đối xứng là giao điểm của các đường chéo.

12. Tính đối xứng trong thế giới tự nhiên

+ Tính đối xứng là sự giống nhau của một hình qua đường trục hoặc qua tâm, tạo nên sự cân bằng.

+ Trong tự nhiên, tính đối xứng được thể hiện rất đa dạng, phong phú, chẳng hạn: con bướm, cầu vồng, sao biển,...

+ Tính đối xứng của một đối tượng là một trong những dấu hiệu quan trọng nhất giúp chúng ta nhanh chóng định hình đối tượng đó khi nhìn vào nó. Ngoài ra, với con người, đối xứng tạo ra sự cân bằng, hài hòa, trật tự nhờ đó tạo ra thẩm mĩ.

13. Tính đối xứng trong nghệ thuật, kiến trúc và công nghệ

Nguyên tắc cân bằng là một trong những nguyên tắc quan trọng với nghệ thuật hay kiến trúc.

Bố cục đối xứng thường được sử dụng trong các tác phẩm nghệ thuật hay kiến trúc.

Một số ví dụ:

Trong thiết kế, công nghệ, chúng ta cũng dễ dàng nhận ra các bố cục có tính đối xứng.

Các công trình hay máy móc muốn tồn tại, ổn định, bền vững và có được vẻ đẹp, bắt mắt thì phải chú trọng đến tính cân xứng.

Một số ví dụ:

Xem thêm lời giải bài tập Toán lớp 6 sách Cánh diều hay, chi tiết khác: