Giải Toán 6 Bài 7 (Cánh diều): Phép nhân, phép chia số thập phân
Lời giải bài tập Toán lớp 6 Bài 7: Phép nhân, phép chia số thập phân sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập Toán 6.
Mục lục Giải Toán 6 Bài 7: Phép nhân, phép chia số thập phân
Trả lời câu hỏi giữa bài
Câu hỏi mở đầu trang 52 Toán 6 Tập 2: Inch (đọc là in-sơ, kí hiệu là in) là tên của một đơn vị đo độ dài: 1 in = 2, 54 cm.
Một chiếc ti vi màn hình phẳng có độ dài đường chéo là 52 in.
Độ dài đường chéo của màn hình ti vi là bao nhiêu mét?

Lời giải
Do 1 in = 2,54 cm nên 52 in = 52.2,54 = 132,08 cm.
Đổi 132,08 cm = 1,3208 m.
Vậy độ dài đường chéo của màn hình ti vi là 1,3208m.
Hoạt động 1 trang 52 Toán 6 Tập 2: Đặt tính để tính tích 5,285 . 7,21.
Lời giải:
Ta thường đặt tính rồi tính như sau:

Vậy 5,285 . 7,21 = 38,10485.
Hoạt động 2 trang 52 Toán 6 Tập 2: Nêu quy tắc nhân hai số nguyên cùng dấu; khác dấu.
Lời giải
Quy tắc nhân hai số nguyên cùng dấu:
Nhân hai số nguyên dương chính là nhân hai số tự nhiên khác 0.
Nhân hai số nguyên âm, ta bỏ đi dấu “-“ trước mỗi số, tính tích của hai số nguyên dương vừa nhận được.
Quy tắc nhân hai số nguyên khác dấu:
Bỏ dấu “-“ trước số nguyên âm, giữ nguyên số còn lại. Tính tích của hai số nguyên dương vừa nhận được. Sau đó thêm dấu “-“ trước kết quả nhận được ở bước 2.
Luyện tập vận dụng 1 trang 53 Toán 6 Tập 2: Tính tích:
b) 19,427.1,8.
Lời giải
a) 8,15.(– 4,26)
= – (8,15.4,26)
Đặt tính:
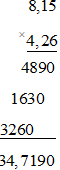
Vậy 8,15.(– 4,26) = – 34,719.
b) 19,427.1,8
Đặt tính:
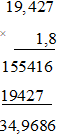
Vậy 19,427.1,8 = 34,9686.
Hoạt động 3 trang 53 Toán 6 Tập 2: Hãy nêu tính chất của phép nhân số nguyên...
Lời giải
Tính chất phép nhân số nguyên:
– Tính chất giao hoán;
– Tính chất kết hợp;
– Nhân với số 1;
– Tính chất phân phối của phép nhân với phép cộng.
Luyện tập vận dụng 2 trang 53 Toán 6 Tập 2: Tính một cách hợp lí:
b) 0,125 . 14 . 36.
Lời giải
a) 0,25.12
= 0,25 . 4 . 3
= (0,25 . 4) .3
= 1.3
= 3.
b) 0,125 . 14 . 36.
= 0,125. 7 .2 . 4.9
= 0,125.7.(2.4).9
= 0,125.7.8.9
= 0,125. 8. 7. 9
= 1.7. 9
= 63.
Hoạt động 4 trang 53 Toán 6 Tập 2: Đặt tính để tính thương: 247,68 : 144.
Lời giải
Ta thường đặt tính rồi tính như sau:
· Lấy 247 chia cho 144 được 1, viết l;
Lấy 1 nhân với 144 được 144;
Lấy 247 trừ đi 144 được 103, viết 103.
· Viết dấu “,” vào bên phải số 1.
· Hạ chữ số 6, được 1 036;
Lấy 1 036 chia cho 144 được 7, viết 7;
Lấy 7 nhân với 144 được 1 008;
Lấy 1 036 trừ đi 1 008 được 28, viết 28.
· Hạ chữ số 8 được 288;
Lấy 288 chia cho 144 được 2, viết 2;
Lấy 2 nhân với 144 được 288;
Lấy 288 trừ đi 288 được 0; viết 0.

Vậy 247,68 : 144 = 1,72.
Hoạt động 5 trang 54 Toán 6 Tập 2: Đặt tính để tính thương: 311,01 : 0,3.
Ta thường đặt tính rồi tính như sau:
· Số chia có một chữ số sau dấu “,” nên ta chuyển dấu “,” ở số bị chia sang bên phải một chữ số
311,01 ⇒ 3110,1
· Bỏ dấu “,” ở số chia
0,3 ⇒ 3
· Thực hiện phép chia 3110,l : 3.
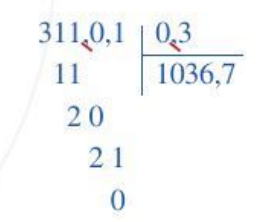
Vậy 311,01 : 0,3 = 1036,7.
Hoạt động 6 trang 55 Toán 6 Tập 2: Nêu quy tắc chia hai số nguyên cùng dấu; khác dấu trong trường hợp phép chia hết.
Lời giải
Quy tắc chia hai số nguyên cùng dấu:
Nếu hai số là hai số nguyên dương thì ta thực hiện chia như hai số tự nhiên khác 0.
Nếu hai số là hai số nguyên âm thì ta bỏ dấu “–“ trước mỗi số và tính thương của hai số nguyên dương vừa nhận được.
Quy tắc chia hai số nguyên khác dấu:
Bỏ dấu “–“ trước số nguyên âm và giữ nguyên số nguyên dương còn lại. Sau đó, tính thương của hai số nguyên dương vừa nhận được. Thêm dấu “–“ vào trước kết quả vừa nhận được.
Luyện tập vận dụng 3 trang 55 Toán 6 Tập 2: Tính thương:
b) ( –15,175) : 12,14.
Lời giải
a) (– 17,01) : (– 12,15) = 17,01: 12,15.
Đặt tính
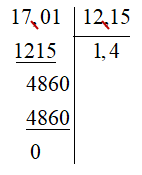
Vậy (– 17,01) : (– 12,15) = 1,4.
b) ( –15,175) : 12,14 = – (15,175 : 12)
Đặt tính:

Vậy ( –15,175) : 12,14 = – 1,25.
Bài tập
Bài 1 trang 55 Toán 6 Tập 2: Tính:
b) (–0,5) . (– 0,7);
c) (–0,8) . 0,006;
d) (–0,4) . (– 0.5) . (– 0,2).
Lời giải
a) 200 . 0,8
Đặt tính:
![]()
Vậy 200.0,8 = 160.
b) (–0,5) . (– 0,7) = 0,5.0,7
Đặt tính:
![]()
Vậy (–0,5) . (– 0,7) = 0,35.
c) (–0,8) . 0,006 = – (0,8 . 0,006)
Đặt tính:
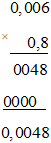
Vậy (–0,8) . 0,006 = – 0,0048.
d) (–0,4) . (– 0.5) . (– 0,2)
= (–0,4) . [(–0,5) . (–0,2)]
= (–0,4). 0,1
= –(0,4.0,1)
= – 0,04.
Vậy (–0,4) . (– 0.5) . (– 0,2) = –0,04.
Bài 2 trang 55 Toán 6 Tập 2: Cho 23. 456 = 10 488. Tính nhẩm:
b) 2,3 .45,6;
c) (–2,3) . (– 4,56);
d) (– 2,3) . 45 600.
Lời giải
Ta có: 23. 456 = 10 488. Khi đó:
a) 2,3 . 456
= 2310.456=23.45610=1048810 = 1 048,8;
b) 2,3 . 45,6
= 2310.45610=23.45610.10=10488100 = 104,88;
c) (–2,3) . (– 4,56) = 2,3 . 4,56
= 2310.456100=23.45610.100=104881000= 10,488;
d) (– 2,3).45 600
= – 2,3.456.100
= −2310.456.100
=−23.456.10010=−104880010=−104880
Bài 3 trang 55 Toán 6 Tập 2: Tính:
b) ( – 72,39) : (– 19);
c) (– 882) : 3,6;
d) 10,88 : (– 0,17).
Lời giải
a) 46,827 : 90
Đặt tính:
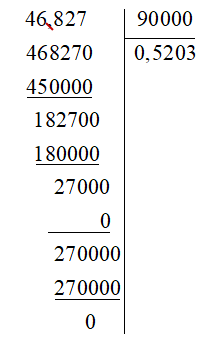
Vậy 46,827 : 90 = 0,5203.
b) ( – 72,39) : (– 19) = 72,39 : 19
Đặt tính:
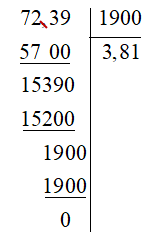
Vậy ( – 72,39) : (– 19) = 3,81.
c) (– 882) : 3,6 = – (882 : 3,6)
Đặt tính:
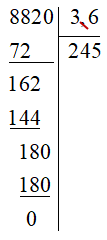
Vậy (– 882) : 3,6 = – 245.
d) 10,88 : (– 0,17) = – (10,88 : 0,17)
Đặt tính:
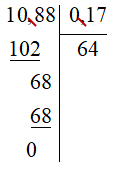
Vậy 10,88 : (– 0,17) = – 64.
Bài 4 trang 56 Toán 6 Tập 2: Cho 182 : 13 = 14. Tính nhẩm:
b) 18,2 : 13.
Lời giải
a) Ta có: 182 : 1,3
=182:1310=182.1013=182.1013=18213.10=14.10=140.
Vậy 182 : 1,3 = 140.
b) Ta có: 18,2 : 13
=18210:13=18210.113=18213.110=14.110=1410=1,4.
Vậy 18,2 : 13 = 1,4.
Bài 5 trang 56 Toán 6 Tập 2: Một căn phòng có dạng hình hộp chữ nhật với chiều dài 4,2 m chiều rộng 3,5 m và chiều cao 3,2 m. Người ta muốn sơn lại trần nhà và bốn bức tường bên trong phòng. Biết rằng tổng diện tích các cửa là 5,4 m2.
a) Tính diện tích cần sơn lại.
b) Giá tiền công sơn lại tường và trần nhà đều là 12 000 đồng/m2. Tính tổng số tiền công để sơn lại căn phòng đó.
Lời giải
Ta có hình vẽ minh họa cho căn phòng hình hộp chữ nhật như sau:
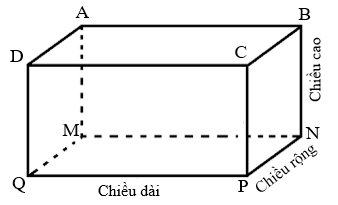
a) Trần nhà ABCD có dạng hình chữ nhật với kích thước 4,2 m và 3,5 m.
Diện tích trần nhà là: 4,2.3,5 = 14,7 m2.
Tường nhà là các hình chữ nhật, trong đó hai bức tường đối diện sẽ có diện tích bằng nhau.
Diện tích hình chữ nhật ABNM bằng diện tích hình chữ nhật DCPQ bằng 4,2.3,2 = 13,44 m2.
Diện tích hình chữ nhật BCPN bằng diện tích hình chữ nhật ADQM bằng 3,5.3,2 = 11,2 m2.
Tổng diện tích tường nhà và trần nhà là: 14,7 + 13,44.2 + 11,2.2 = 63,98 m2.
Diện tích cần sơn lại sẽ là tường nhà trừ đi diện tích các cửa và bằng:
63,98 – 5,4 = 58,58 m2.
Vậy diện tích cần sơn lại là 58,58 m2.
b) Tiền công sơn lại tường và trần nhà là:
58,58 . 12 000 = 702 960 (đồng).
Vậy tiền công sơn lại tường và trần nhà là 702 960 đồng.
Bài 6 trang 56 Toán 6 Tập 2: Một thửa ruộng dạng hình chữ nhật có chiều dài 110 m, chiều rộng 78 m. Người ta cấy lúa trên thửa ruộng đó, cứ 1 ha thu hoạch được 7l,5 tạ thóc. Cả thửa ruộng đó thu hoạch được bao nhiêu tạ thóc?
Lời giải
Diện tích thửa ruộng dạng hình chữ nhật là:
110 . 78 = 8580 (m2).
Ta có 1ha = 10 000 m2.
8580 m2 = 0,8580 ha.
Số thóc thu hoạch được trên thửa ruộng đó là:
0,858.71,5 = 61,347 (tạ thóc).
Vậy cả thửa ruộng thu được 61,347 tạ thóc.
Bài 7 trang 56 Toán 6 Tập 2: Bác Hà có hai tấm kính hình chữ nhật. Chiều rộng của mỗi tấm kính bằng chiều dài của nó và chiều dài của tấm kính nhỏ đúng bằng chiều rộng của tấm kính lớn. Bác ghép hai tấm kính sát vào nhau và đặt lên mặt bàn có diện tích 0,9 m2 thì vừa khít. Tính diện tích của mỗi tấm kính.
Lời giải
Gọi chiều dài của tấm kính lớn là x (m) (x > 0)
Khi đó chiều rộng của tấm kính lớn là: 12x=x2(m).
Diện tích của tấm kính lớn là: x.x2=x.x2=x22(m2).
Vì chiều dài của tấm kính nhỏ đúng bằng chiều rộng của tấm kính lớn và bằng x2(m).
Khi đó chiều rộng của tấm kính nhỏ là: 12.x2=x4(m).
Diện tích của tấm kính lớn là: x2.x4=x.x2.4
Diện tích của tấm kính lớn gấp số lần diện tích của tấm kính nhỏ là: .
Vì ghép hai tấm kính sát vào nhau và đặt lên mặt bàn có diện tích 0,9 m2 thì vừa khít nên tổng diện tích hai tấm kính là bằng 0,9 m2.
Coi diện tích tấm kính nhỏ là một phần thì tấm kính lớn là hai phần vì vậy tổng diện tích hai tấm kính là ba phần. Khi đó, diện tích một phần là: 0,9: 3 = 0,3 (m2).
Suy ra diện tích tấm kính nhỏ là 0,3 m2.
Từ đó diện tích tấm kính lớn là: 0,3.2 = 0,6 m2.
Vậy diện tích tấm kính nhỏ là 0,3 m2 và diện tích tấm kính lớn là 0,6 m2.
Bài 8 trang 56 Toán 6 Tập 2: Một chiếc bàn ăn có mặt bàn hình tròn đường kính 150 cm.

Lời giải
Đường kính của khăn vải bằng đường kính của mặt bàn cộng với độ dài hai phần khăn rủ xuống là: 150 + 20 + 20 = 190 (cm).
Bán kính của khăn vải là: 190:2 = 95 (cm).
Diện tích của chiếc khăn trải bàn là: .
Bán kính của mặt bàn là: 150 : 2 = 75 (cm).
Diện tích mặt bàn là: .
Diện tích phần khăn rủ xuống khỏi mặt bàn là: 28338,5 – 17662,5 = 10 676 (cm2).
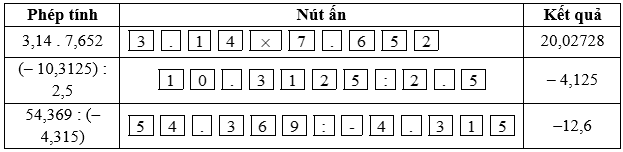
Dùng máy tính cầm tay để tính:
(– 10,3125) : 2,5;
54,369 : (– 4,315).
Lời giải
Bằng cách sử dụng máy tính cầm tay, ta có bảng kết quả sau:
Lý thuyết Toán 6 Bài 7: Phép nhân, phép chia số thập phân đơn giản - Cánh diều
1. Phép nhân số thập phân
a) Nhân hai số thập phân
Muốn nhân hai số thập phân dương, ta làm như sau:
Bước 1: Viết thừa số này ở dưới thừa số kia như đối với phép nhân các số tự nhiên
Bước 2: Thực hiện phép nhân như nhân số tự nhiên
Bước 3: Đếm xem trong phần thập phân ở cả hai thừa số có tất cả bao nhiêu chữ số rồi dùng dấu “,” tách ở tích ra bấy nhiêu chữ số từ phải sang trái, ta nhận được tích cần tìm.
Chú ý: Hai số thập phân cùng dấu thì tích là số dương; hai số thập phân khác dấu thì tích là số âm.
Nhân hai số thập phân cùng dấu: (‒a) . (‒b) = a.b với a, b > 0
Nhân hai số thập phân khác dấu: (‒a) . b = a.(‒b) = ‒ (a.b) với a, b > 0
Ví dụ 1: Tính tích:
a) (‒2,564) . (‒1,45);
b) (‒4,89) . 9,3.
Hướng dẫn giải
a) (‒2,564) . (‒1,45) = 2,564 . 1,45 = 3,7178.
b) (‒4,89) . 9,3 = ‒(4,89 . 9,3) = ‒ 45,477
b) Tính chất của phép nhân số thập phân
Phép nhân số thập phân cũng có các tính chất như phép nhân số nguyên: giao hoán, kết hợp, nhân với số 1, phân phối của phép nhân với phép cộng và phép trừ.
Ví dụ 2. Tính một cách hợp lí:
a) 1,25 . 24;
b) 1,14. 10,6 + 1,14 . (‒0,6).
Hướng dẫn giải:
a) 1,25 . 24 = 5 . 0,25 . 4 . 6 = (0,25.4) . (5.6) = 1 . 30 = 30.
b) 1,14. 10,6 + 1,14 . (‒0,6)
= 1,14 . [10,6 + (‒0,6)]
= 1,14 . 10
= 11,4.
2. Phép chia số thập phân
Muốn chia hai số thập phân dương, ta làm như sau:
Bước 1: Số chia có bao nhiêu chữ số sau dấu “,” thì chuyển dấu “,” ở số bị chia sang bên phải bấy nhiêu chữ số. (Khi chuyển dấu “,” ở số bị chia sang phải mà số bị chia không đủ vị trí, thì ta điền thêm những chữ số 0 vào bên phải của số đó)
Bước 2: Bỏ đi dấu “,” ở số chia, ta nhận được số nguyên dương
Bước 3: Đem số nhận được ở Bước 1 chia cho số nguyên dương nhận được ở Bước 2, ta có thương cần tìm.
Chú ý: Hai số thập phân cùng dấu thì thương là số dương; hai số thập phân khác dấu thì thương là số âm.
Chia hai số thập phân cùng dấu: (‒a) : (‒b) = a : b với a, b > 0
Chia hai số thập phân khác dấu: (‒a) : b = a : (‒b) = ‒ (a : b) với a, b > 0
Ví dụ 3. Tính thương:
a) (‒4,5625) : (‒1,25);
b) (‒23,04) : 0,036.
Hướng dấn giải
a) (‒4,5625) : (‒1,25) = 4,5625 : 1,25 = 456,25 : 125 = 3,65.
b) (‒23,04) : 0,036 = ‒ (23,04 : 0,036) = ‒ (23040 : 36) = ‒ 640.
3. Thứ tự thực hiện phép tính với số thập phân:
a) Thứ tự thực hiện phép tính với số thập phân trong biểu thức không chứa dấu ngoặc:
Đối với biểu thức không chứa dấu ngoặc, ta thực hiện theo thứ tự:
Luỹ thừa → Phép nhân và phép chia → Phép cộng và phép trừ.
b) Thứ tự thực hiện phép tính với số thập phân trong biểu thức có chứa dấu ngoặc:
Đối với biểu thức có chứa dấu ngoặc, ta thực hiện theo thứ tự:
Dấu ngoặc () → Dấu ngoặc [] → Dấu ngoặc {}.
Ví dụ 4. Tính: 1,23 + (‒6,2725) : 0,65 – 1,52
Hướng dấn giải
1,23 + (‒6,2725) : 0,65 – 1,52
= 1,23 + [‒(6,2725 : 0,65)] – 1,5.1,5
= 1,23 – 9,65 – 2,25
= 1,23 + (‒9,65) + (‒2,25)
= ‒ (9,65 – 1,23) + (‒2,25)
= (‒8,42) + (‒2,25)
= ‒ (8,42 + 2,25)
= ‒ 10,67.
Xem thêm lời giải bài tập Toán lớp 6 sách Cánh diều hay, chi tiết khác:
Bài 8: Ước lượng và làm tròn số
Bài 10: Hai bài toán về phân số
Hoạt động thực hành và trải nghiệm Chủ đề 2. Chỉ số khối cơ thể (BMI)
Xem thêm các chương trình khác:
- Soạn văn lớp 6 (hay nhất) - Cánh diều
- Soạn văn lớp 6 (ngắn nhất) - Cánh diều
- Bố cục tác phẩm Ngữ văn 6 – Cánh Diều
- Nội dung chính tác phẩm Ngữ văn lớp 6 – Cánh Diều
- Tóm tắt tác phẩm Ngữ văn lớp 6 – Cánh Diều
- Tác giả tác phẩm Ngữ văn lớp 6 – Cánh Diều
- Văn mẫu lớp 6 – Cánh Diều
- Giải VBT Luyện viết Ngữ văn lớp 6 – Cánh diều
- Giải sgk Lịch Sử 6 – Cánh Diều
- Giải sbt Lịch Sử 6 – Cánh Diều
- Giải VBT Lịch sử 6 – Cánh diều
- Lý thuyết Lịch sử lớp 6 – Cánh diều
- Giải sbt Địa Lí 6 – Cánh Diều
- Giải sgk Địa Lí 6 – Cánh Diều
- Lý thuyết Địa Lí 6 – Cánh Diều
- Giải VBT Địa lí 6 – Cánh diều
- Giải sgk GDCD 6 – Cánh Diều
- Lý thuyết GDCD 6 – Cánh diều
- Giải sbt Giáo dục công dân 6 – Cánh diều
- Giải sgk Công nghệ 6 – Cánh Diều
- Lý thuyết Công nghệ 6 – Cánh Diều
- Giải sgk Khoa học tự nhiên 6 – Cánh Diều
- Giải sbt Khoa học tự nhiên 6 – Cánh Diều
- Lý thuyết Khoa học tự nhiên 6 – Cánh Diều
- Giải sgk Tin học 6 – Cánh Diều
- Lý thuyết Tin học 6 – Cánh Diều
- Giải sgk Tiếng Anh 6 - ilearn Smart World
- Ngữ pháp Tiếng Anh 6 i-learn Smart World
- Trọn bộ Từ vựng Tiếng Anh 6 ilearn Smart World đầy đủ nhất
- Giải sbt Tiếng Anh 6 - iLearn Smart World
- Bài tập Tiếng Anh 6 iLearn Smart World theo Unit có đáp án
