Nội dung bài viết

    Xem thêm

    Tìm đa thức Q(x) sao cho P(x).Q(x) = R(x), biết: a) P(x) = x – 2, R(x) = –x^3 + 8; b) P(x) = x^2 – 3x + 2

    Lời giải Bài 59 trang 56 SBT Toán 7 Tập 1 sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 7.

    1 2,452 31/12/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Giải SBT Toán 7 Cánh diều Bài tập cuối chương 6

    Bài 59 trang 56 SBT Toán 7 Tập 1:

    Tìm đa thức Q(x) sao cho P(x).Q(x) = R(x), biết:

    a) P(x) = x – 2, R(x) = –x3 + 8;

    b) P(x) = x2 – 3x + 2, R(x) = 10 – 13x + 2x2 + x3.

    Lời giải

    Ta có P(x).Q(x) = R(x)

    Suy ra Q(x) = R(x) : P(x).

    a) Với P(x) = x – 2, R(x) = –x3 + 8 ta có:

    Q(x) = (–x3 + 8) : (x – 2)

    Ta thực hiện đặt tính chia đa thức như sau:

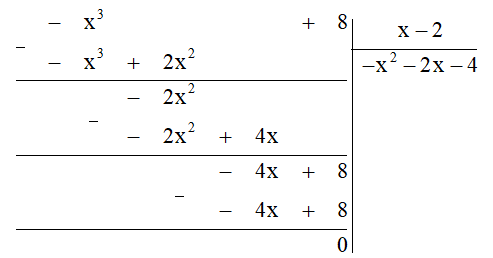
    Sách bài tập Toán 7 (Cánh diều): Bài tập cuối chương 6  (ảnh 1)

    Khi đó Q(x) = (–x3 + 8) : (x – 2) = – x2 – 2x – 4.

    Vậy Q(x) = – x2 – 2x – 4.

    b) Với P(x) = x2 – 3x + 2, R(x) = 10 – 13x + 2x2 + x3 ta có:

    Q(x) = (10 – 13x + 2x2 + x3) : (x2 – 3x + 2)

             = (x3 + 2x2 – 13x + 10) : (x2 – 3x + 2)

    Ta thực hiện đặt tính chia đa thức như sau:

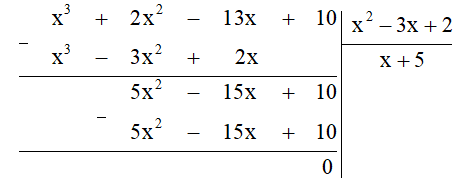
    Sách bài tập Toán 7 (Cánh diều): Bài tập cuối chương 6  (ảnh 1)

    Khi đó Q(x) = (x3 + 2x2 – 13x + 10) : (x2 – 3x + 2) = x + 5.

    Vậy Q(x) = x + 5.

    Xem thêm lời giải sách bài tập Toán lớp 7 Cánh diều hay, chi tiết khác: 

    Bài 50 trang 55 SBT Toán 7 Tập 1:  Giá trị của biểu thức (x2 – 8)(x + 3) – (x – 2)(x + 5) tại x = 3 là: A. – 2 B. 16 C. – 10 D. 10...

    Bài 51 trang 55 SBT Toán 7 Tập 1:  Biểu thức nào sau đây là đa thức một biến? Tìm biến và bậc của đa thức đó. a) – 2 022x; b) – 6x2 – 4x + 2; c) 3un – 8u2 – 20 (n ∈ ℕ, n > 2)...

    Bài 52 trang 55 SBT Toán 7 Tập 1: Tính giá trị của biểu thức: a) A = 56 – 5a + 6b tại a = 22, b = 23; b) B = 6xyz – 3xy – 19z tại x = 11, y = 32, z = 0...

    Bài 53 trang 55 SBT Toán 7 Tập 1: Một bể đang chứa 500 l nước. Người ta mở một vòi nước cho chảy vào bể đó, mỗi phút vòi nước đó chảy vào bể được 50 l nước...

    Bài 54 trang 55 SBT Toán 7 Tập 1: Viết đa thức biến x trong mỗi trường hợp sau: a) Đa thức bậc nhất có hệ số của biến bằng – 7 và hệ số tự do bằng 0...

    Bài 55* trang 55 SBT Toán 7 Tập 1:  Tìm giá trị của m để đa thức sau là đa thức bậc ba theo biến x: P(x) = (m2 – 25)x4 + (20 + 4m)x3  +17x2 – 23...

    Bài 56 trang 55 SBT Toán 7 Tập 1:  Cho đa thức A(x) = – 11x5 + 4x3 – 12x2 + 11x5 + 13x2 – 7x + 2.  a) Thu gọn và sắp xếp đa thức A(x) theo số mũ giảm dần của biến...

    Bài 57 trang 56 SBT Toán 7 Tập 1:  Tính: a) (– 4x3 – 13x2 + 2x5) + (13x2 + 2x3 – 12x – 1);  b) (12x6 – 11x2 + 3x3 + 9) – (13x6 + 2x3 – 11x2 – 11x)...

    Bài 58 trang 56 SBT Toán 7 Tập 1:  Tìm đa thức C(x) sao cho A(x) – C(x) = B(x), biết: a) A(x) = x3 + x2 + x – 2, B(x) = 9 – 2x + 11x3 + x4...

    Bài 59 trang 56 SBT Toán 7 Tập 1:  Tìm đa thức Q(x) sao cho P(x).Q(x) = R(x), biết: a) P(x) = x – 2, R(x) = –x3 + 8;  b) P(x) = x2 – 3x + 2, R(x) = 10 – 13x + 2x2 + x3...

    Bài 60 trang 56 SBT Toán 7 Tập 1:  Tìm hệ số a sao cho đa thức G(x) = x4 + x2 + a chia hết cho đa thức M(x) = x2 – x + 1...

    Bài 61 trang 56 SBT Toán 7 Tập 1:  Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai? a) x = 2 và x = –3 là nghiệm của đa thức P(x) = x2 – 5x + 6...

    Bài 62 trang 56 SBT Toán 7 Tập 1:  Cho đa thức P(x) = ax4 + bx3 + cx2 + dx + e (a ≠ 0) với a + b + c + d + e = 0. Chứng tỏ rằng x = 1 là nghiệm của đa thức P(x)...

    Bài 63 trang 56 SBT Toán 7 Tập 1:  Cho đa thức Q(x) = ax2 + bx + c (a ≠ 0). Chứng minh rằng nếu Q(x) nhận 1 và –1 là nghiệm thì a và c là hai số đối nhau...

    Bài 64 trang 56 SBT Toán 7 Tập 1:  Một cửa hàng bán hoa sau khi tăng giá 50 nghìn đồng mỗi chậu hoa so với giá bán ban đầu là 3x (nghìn đồng) thì số tiền thu được là 3x2 + 53x + 50...

    Bài 65 trang 56, 57 SBT Toán 7 Tập 1:  Tháng 5 năm 2019, nhiều đại biểu trên cả nước đã “hội quân” trên một tàu kiểm ngư rời cảng biển quốc tế Cam Ranh để bắt đầu...

    Bài 66 trang 57 SBT Toán 7 Tập 1:  Lượng khí thải gây hiệu ứng nhà kính do các hoạt động của con người là nguyên nhân gây ra nhiệt độ Trái Đất tăng một cách đáng kể...

    Bài 67 trang 57 SBT Toán 7 Tập 1:  Giá bán lẻ 1 hộp sữa là 7 000 đồng, giá cho 1 lốc sữa 4 hộp là 26 000 đồng. Nếu mua từ 4 lốc sữa trở lên thì cứ 2 lốc sữa được tặng 1 hộp...

    Bài 68 trang 57 SBT Toán 7 Tập 1:  Nhân dịp cuối năm, một cửa hàng cần thanh lí một lô hàng (gồm 100 sản phẩm cùng loại) với giá bán là x đồng/chiếc...

    Bài 69 trang 57 SBT Toán 7 Tập 1:  Tính diện tích của hình thang ABCD với các số đo cho như Hình 7 theo x...

    Xem thêm lời giải sách bài tập Toán lớp 7 Cánh diều hay, chi tiết khác: 

    Bài 5. Phép chia đa thức một biến

    Bài tập cuối chương 6

    Bài 1. Tổng các góc của một tam giác

    Bài 2. Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác

    Bài 3. Hai tam giác bằng nhau

    Tham khảo các loạt bài Toán 7 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 2,452 31/12/2022
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: