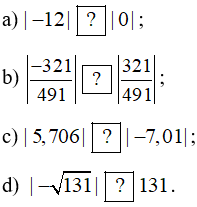Sách bài tập Toán 7 Bài 3 (Cánh diều): Giá trị tuyệt đối của một số thực

Giải sách bài tập Toán lớp 7 Bài 3: Giá trị tuyệt đối của một số thực - Cánh diều

Giải SBT Toán 7 trang 45 Tập 1

Bài 19 trang 45 SBT Toán 7 Tập 1: Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai? Vì sao?

a) Giá trị tuyệt đối của một số thực là một số dương hoặc bằng 0.

b) Hai số có giá trị tuyệt đối bằng nhau là hai số bằng nhau.

c) Giá trị tuyệt đối của một số thực luôn bằng chính nó.

Lời giải:

a) Đúng. Do giá trị tuyệt đối của một số thực là một số không âm.

b) Sai. Do hai số có giá trị tuyệt đối bằng nhau là hai số bằng nhau hoặc đối nhau.

c) Đúng. Do hai số đối nhau có điểm biểu diễn cách đều điểm gốc 0 nên giá trị tuyệt đối của chúng bằng nhau.

d) Sai. Do giá trị tuyệt đối của số âm là số đối của nó.

Bài 20 trang 45 SBT Toán 7 Tập 1: Tìm:

Lời giải:

Ta có:

Bài 21 trang 45 SBT Toán 7 Tập 1: Biểu diễn trên trục số giá trị tuyệt đối của mỗi số đã cho trên trục số ở Hình 3:

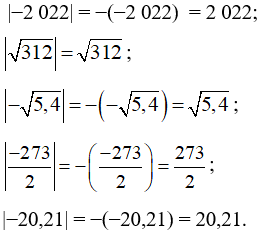
Lời giải:

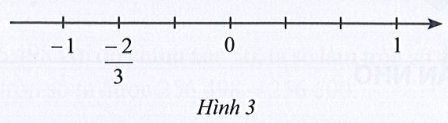
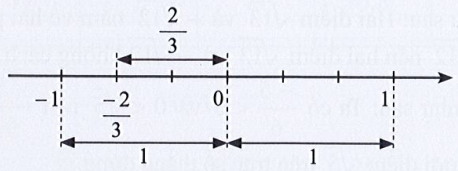
Trên trục số ở Hình 3 có các điểm −1; $-\frac{2}{3}$; 0; 1.

Giá trị tuyệt đối của các số −1; $\frac{-2}{3}$; 0; 1 lần lượt là 1; $\frac{2}{3}$; 0; 1.

Ta biểu diễn giá trị tuyệt đối của các số −1; $-\frac{2}{3}$; 0; 1 trên trục số như sau:

Bài 22 trang 45 SBT Toán 7 Tập 1: Tính giá trị của mỗi biểu thức:

a) |−11| + |22| + |−33| − 44;

b) 2 . |−21| − 3 . |125| − 5 . |−33| − |2 . 21|;

c) $2,8+3.\left|-\frac{13}{3}\right|+0,2.\left|6\right|+5.|-10|$;

d) $(-1,5)+2.\left|2\frac{1}{2}\right|$$-6.\left|\frac{-16}{3}\right|+5.|-0,3|$.

Lời giải:

a) |−11| + |22| + |−33| − 44

= 11 + 22 + 33 – 44

= 33 + 33 – 44

= 66 – 44 = 22.

b) 2 . |−21| − 3 . |125| − 5 . |−33| − |2 . 21|

= 2 . 21 − 3 . 125 − 5 . 33 – 42

= 42 – 375 – 165 – 42

= – 333 – 165 – 42

= – 498 – 42 = – 540.

c) 

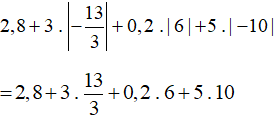
= 2,8 + 13 + 1,2 + 50

= 15,8 + 1,2 + 50

= 17 + 50 = 67.

d) 

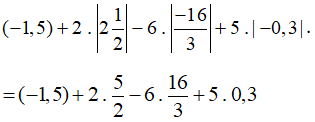
= −1,5 + 5 – 32 + 1,5

= (−1,5 + 1,5) + (5 – 32)

= 0 – 27 = – 27.

Bài 23 trang 45 SBT Toán 7 Tập 1: Trong giờ hoạt động của câu lạc bộ Toán, bạn Nam phát biểu "Giá trị tuyệt đối của tổng hai số thực khác dấu bất kì luôn là một số dương". Bạn Nam phát biểu đúng hay sai? Vì sao?

Lời giải:

Phát biểu của bạn Nam là sai do giá trị tuyệt đối của tổng hai số đối là 0.

Chẳng hạn: |2 + (−2)| = |0| = 0.

Bài 24 trang 45 SBT Toán 7 Tập 1: Chọn dấu "<", ">", "=" thích hợp cho $\boxed{?}$:

Lời giải:

a) Ta có: |−12| = 12 > 0 = |0|.

Do đó $|-12|\boxed{>}\left|0\right|$;

b) Ta có $\left|\frac{-321}{491}\right|=\frac{321}{491};\left|\frac{321}{491}\right|=\frac{321}{491}$.

Do đó $\left|\frac{-321}{491}\right|\boxed{=}\left|\frac{321}{491}\right|$;

c) Ta có: |5,706| = 5,706; |−7,01| = 7,01.

Vì 5,706 < 7,01 nên |5,706| < |−7,01|.

Vậy $|5,706|\boxed{<}|-7,01|$;

d) Ta có: $|-\sqrt{131}|=\sqrt{131}=11,\mathrm{4455...}$

Vì 11,4455 < 131 nên $\sqrt{131}<131$.

Vậy $|-\sqrt{131}|\boxed{<}131$.

Bài 25 trang 45 SBT Toán 7 Tập 1: Tìm số thực x, biết:

a) $\left|x\right|=\frac{13}{17}$;

b) |x + 2,037| = 0;

c) $|x-22|=-\sqrt{3}$;

d) |x| = x;

e*) |x| + |x + 1| = 0.

Lời giải:

a) Do $\left|x\right|=\frac{13}{17}$

Nên $x=\frac{13}{17}$ hoặc $x=-\frac{13}{17}$.

b) Do |x + 2,037| = 0 nên x + 2,037 = 0.

Suy ra x = − 2,037.

c) Vì |x – 22| ≥ 0 với mọi số thực x.

Mà $-\sqrt{3}<0$ nên không có giá trị nào của x thỏa mãn $|x-22|=-\sqrt{3}$.

d) Ta có |x| = x với mọi số thực x không âm.

Vậy x ≥ 0.

e*) Do |x| ≥ 0, |x + 1| ≥ 0 với mọi số thực x.

Nên |x| + |x + 1| ≥ 0 với mọi số thực x.

Do đó |x| + |x + 1| = 0 khi |x| = 0 và |x + 1| = 0.

Suy ra x đồng thời bằng 0 và bằng –1 (vô lí).

Vậy không có giá trị nào của x thỏa mãn yêu cầu của đề bài.

Giải SBT Toán 7 trang 46 Tập 1

Bài 26 trang 46 SBT Toán 7 Tập 1: Cho hai số thực a, b (a ≠ 0, b ≠ 0, a ≠ b). Gọi $M=\sqrt{19}.\left|a\right|.b^2.{(a-b)}^2$. Chứng tỏ rằng M là số dương.

Lời giải:

Ta có $\sqrt{19}>0$ và |a| > 0, b² > 0, (a – b)² > 0 với mọi số thực a, b thỏa mãn a ≠ 0, b ≠ 0, a ≠ b.

Do đó $\sqrt{19}.\left|a\right|.b^2.{(a-b)}^2>0$.

Vậy M là số dương.

Bài 27* trang 46 SBT Toán 7 Tập 1: Cho 100 số thực, trong đó tích của ba số bất kì là một số âm. Chứng tỏ rằng tích của 100 số thực đó là một số dương.

Lời giải:

Do trong 100 số thực đã cho thì tích của ba số bất kì là một số âm nên trong 100 số thực đó có ít nhất một số âm.

Ta gọi số âm đó là a.

Tách riêng số a, chia 99 số còn lại thành 33 nhóm, mỗi nhóm gồm 3 số.

Khi đó, tích của mỗi nhóm là một số âm.

Suy ra tích của 99 số trong 33 nhóm cũng là một số âm.

Do đó, tích của của số âm a và 99 số còn lại là một số dương.

Vậy tích của 100 số thực đã cho là một số dương.

Bài 28* trang 46 SBT Toán 7 Tập 1:

a) Với giá trị nào của x thì A = 10 . |x – 2| + 22 đạt giá trị nhỏ nhất?

b) Với giá trị nào của x thì B = – (21x² + 22 . |x|) – 23 đạt giá trị lớn nhất?

Lời giải:

a) Nhận xét: Với các số thực a, b, c, d, nếu a ≥ b, c ≥ d thì a + c ≥ b + d.

Ta có: |x – 2| ≥ 0 với mọi số thực x nên A = 10 . |x – 2| + 22 ≥ 22 với mọi số thực x.

Vậy giá trị nhỏ nhất của A là 22.

Dấu "=" xảy ra khi và chỉ khi |x – 2| = 0. Suy ra x – 2 = 0 hay x = 2.

b) Nhận xét: Với hai số thực a, b, nếu a ≥ b thì –a ≤ –b.

Ta có: x² ≥ 0, |x| ≥ 0 với mọi số thực x.

Nên 21x² + 22 . |x| ≥ 0 hay – (21x² + 22 . |x|) ≤ 0 với mọi số thực x.

Suy ra B = – (21x² + 22 . |x|) – 23 ≤ – 23 với mọi số thực x.

Vậy giá trị lớn nhất của B là – 23.

Dấu "=" xảy ra khi và chỉ khi x² = 0 và |x| = 0. Suy ra x = 0

Xem thêm lời giải sách bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:

Bài 2: Tập hợp ℝ các số thực

Bài 4: Làm tròn và ước lượng

Bài 5: Tỉ lệ thức

Bài 6: Dãy tỉ số bằng nhau

Bài 7: Đại lượng tỉ lệ thuận

Xem thêm tài liệu Toán lớp 7 Cánh diều hay, chi tiết khác:

Lý thuyết Bài 3. Giá trị tuyệt đối của một số thực