Sách bài tập Toán 7 Bài 1 (Cánh diều): Biểu thức số. Biểu thức đại số 

Giải sách bài tập Toán 7 Bài 1. Biểu thức số. Biểu thức đại số

Bài 1 trang 37 SBT Toán 7 Tập 1: 

Trống đồng Ngọc Lũ là một trong những chiếc trống đồng cổ hiện được lưu trữ ở Bảo tàng Lịch sử Quốc gia. Mặt chiếc trống đồng Ngọc Lũ đó có dạng hình tròn với đường kính 79,3 cm. Biểu thức số nào sau đây biểu thị diện tích của mặt chiếc trống đồng Ngọc Lũ đó (lấy π = 3,14)?

a) (79,3 : 2)² . 3,14 (cm²).

b) (79,3)² . 3,14 (cm²).

Lời giải

Mặt chiếc trống đồng Ngọc Lũ đó có dạng hình tròn với đường kính 79,3 cm nên có bán kính là 79, 3 : 2 (cm).

Khi đó diện tích của mặt chiếc trống đồng Ngọc Lũ đó là:

(79,3 : 2)² . π = (79,3 : 2)² . 3,14 (cm²).

Vậy biểu thức số biểu thị diện tích của mặt chiếc trống đồng Ngọc Lũ đó là:

(79,3 : 2)² . 3,14 (cm²).

Ta chọn a).

Bài 2 trang 37 SBT Toán 7 Tập 1: 

Viết biểu thức số biểu thị diện tích phần bể được lát gạch (xung quanh bể và đáy bể) của một bể bơi có dạng hình hộp chữ nhật với chiều dài 15 m, chiều rộng 10 m và chiều cao 1,2 m (biết diện tích phần mạch vữa không đáng kể).

Lời giải

Biểu thức số biểu thị diện tích đáy của bể là: 15 . 10 (m²).

Biểu thức số biểu thị diện tích xung quanh của bể là:

2 . (15 + 10) . 1,2 (m²).

Vậy biểu thức số biểu thị diện tích phần bể được lát gạch (xung quanh bể và đáy bể) của một bể bơi là: 2 . (15 + 10) . 1,2 + 15 . 10 (m²).

Bài 3 trang 37 SBT Toán 7 Tập 1: 

Mỗi ngày lượng nước một người cần uống (tính theo đơn vị lít) bằng khối lượng cơ thể (tính theo đơn vị ki-lô-gam) nhân với 0,03, sau đó cộng với lượng nước tăng cường cho thời gian vận động (cứ mỗi 30 phút vân động cộng thêm 0,335 l nước).

(Nguồn: https://24hthongtin.com/co-the-can-cung-cap-bao-nhieu-nuoc-moi-ngay.html)

a) Em Dung 7 tuổi nặng 23 kg, mỗi ngày em đạp xe 15 phút và tham gia các hoạt động vận động khác trong 105 phút. Viết biểu thức số biểu thị lượng nước em Dung cần uống mỗi ngày.

b) Áp dụng cách tính trên, hãy tính lượng nước mà mỗi thành viên trong gia đình em cần uống mỗi ngày.

Lời giải

a) Thời gian vận động của em Dung là: 15 + 105 (phút).

Khi đó biểu thức số biểu thị lượng nước em Dung cần uống mỗi ngày là:

23 . 0,03 + $\frac{15+105}{30}$ . 0,335 (l).

b) Học sinh tự thực hiện tương tự như phần a).

Bài 4 trang 37 SBT Toán 7 Tập 1:

Một ngày mùa hè người ta đo được nhiệt độ vào buổi sáng là t °C, buổi trưa nhiệt độ tăng thêm 3 °C so với buổi sáng và buổi đêm nhiệt độ giảm đi y °C so với buổi trưa.

a) Viết biểu thức đại số biểu thị nhiệt độ lúc buổi đêm của ngày mùa hè đó.

b) Tính nhiệt độ lúc buổi đêm của ngày mùa hè đó, biết t = 30 và y = 5.

Lời giải

a) Nhiệt độ vào buổi sáng là t °C, buổi trưa nhiệt độ tăng thêm 3 °C so với buổi sáng nên nhiệt độ buổi trưa là: t + 3 (°C).

Buổi đêm nhiệt độ giảm đi y °C so với buổi trưa nên nhiệt độ buổi đêm là: t + 3 – y (°C).

Vậy biểu thức đại số biểu thị nhiệt độ lúc buổi đêm của ngày mùa hè đó là t + 3 – y (°C).

b) Thay t = 30 và y = 5 vào biểu thức t + 3 – y ta có nhiệt độ lúc buổi đêm của ngày mùa hè đó là: 30 + 3 – 5 = 28 (°C).

Vậy nhiệt độ lúc buổi đêm của ngày mùa hè khi t = 30 và y = 5 là 28 °C.

Bài 5 trang 38 SBT Toán 7 Tập 1: 

Viết biểu thức đại số biểu thị:

a) Tổng các bình phương của x và y;

b) Tổng của x và y bình phương;

c) Tổng các lập phương của x và y;

d) Lập phương của tổng x và y.

Lời giải

a) Biểu thức đại số biểu thị bình phương của x là: x²;

Biểu thức đại số biểu thị bình phương của y là: y²;

Vậy biểu thức đại số biểu thị tổng các bình phương của x và y là: x² + y².

b) Biểu thức đại số biểu thị y bình phương là: y²;

Vậy biểu thức đại số biểu thị tổng của x và y bình phương là: x + y².

c) Biểu thức đại số biểu thị lập phương của x là: x³;

Biểu thức đại số biểu thị lập phương của y là: y³;

Vậy biểu thức đại số biểu thị tổng các lập phương của x và y là: x³ + y³.

d) Biểu thức đại số biểu thị tổng x và y là: x + y;

Vậy biểu thức đại số biểu thị lập phương của tổng x và y là: (x + y)³.

Bài 6 trang 38 SBT Toán 7 Tập 1: 

a) Biểu thức đại số biểu thị diện tích của hình thang có đáy lớn 2a (m), đáy bé b (m), đường cao 2h (m) là:

A. (a + b) . h (m²);

B. $\frac{1}{2}$(2a + b) . h (m²) ;

C. (2a + b) . h (m²);

D. (a + 2b) . h (m²).

b) Biểu thức đại số biểu thị tích của tổng x và y với hiệu của x và y là:

A. x + y . x – y;

B. (x + y)(x – y);

C. (x + y)x – y;

D. xy(x + y)(x – y).

Lời giải

a) Đáp án đúng là: C

Biểu thức đại số biểu thị diện tích của hình thang có đáy lớn 2a (m), đáy bé b (m), đường cao 2h (m) là:

$\frac{1}{2}$ (2a + b) . 2h = (2a + b) . h (m²).

Vậy ta chọn C.

b) Đáp án đúng là: B

Biểu thức đại số biểu thị tổng của x và y là x + y.

Biểu thức đại số biểu thị hiệu của x và y là x – y.

Biểu thức đại số biểu thị tích của tổng x và y với hiệu của x và y là: (x + y)(x – y).

Vậy ta chọn B.

Bài 7 trang 38 SBT Toán 7 Tập 1: 

Cô Hà có x kg mơ. Để làm ô mai mơ gừng chua ngọt, cô Hà cần chuẩn bị thêm lượng đường trắng bằng $\frac{1}{2}$ lượng mơ, lượng gừng tươi bằng $\frac{1}{2}$ lượng mơ, lượng muối bằng $\frac{1}{10}$ lượng mơ.

a) Viết biểu thức biểu thị khối lượng các nguyên liệu cô Hà cần chuẩn bị thêm theo x.

b) Nếu cô Hà có 15 kg mơ để làm ô mai thì khối lượng các nguyên liệu cần chuẩn bị thêm là bao nhiêu?

Lời giải

a) Cô Hà có x kg mơ.

Lượng đường trắng cô Hà cần chuẩn bị là $\frac{1}{2}$x (kg);

Lượng gừng tươi cô Hà cần chuẩn bị là $\frac{1}{2}$x (kg);

Lượng muối cô Hà cần chuẩn bị là $\frac{1}{10}$x (kg).

Biểu thức biểu thị khối lượng các nguyên liệu cô Hà cần chuẩn bị thêm là:

$\frac{1}{2}$x + $\frac{1}{2}$x + $\frac{1}{10}$x (kg).

b) Nếu cô Hà có 15 kg mơ thì x = 15 (kg).

Khi đó ta có khối lượng các nguyên liệu cần chuẩn bị thêm là:

$\frac{1}{2}$.15 + $\frac{1}{2}$.15 + $\frac{1}{10}$.15 = 7,5 + 7,5 + 1,5 = 16,5 (kg).

Vậy nếu cô Hà có 15 kg mơ để làm ô mai thì khối lượng các nguyên liệu cần chuẩn bị thêm là 16,5 kg.

Bài 8 trang 38 SBT Toán 7 Tập 1: 

Một mảnh vườn có dạng hình chữ nhật với chiều dài x (m), chiều rộng bằng $\frac{3}{5}$ chiều dài. Ở giữa vườn người ta xây một cái bể hình tròn đường kính d (m).

a) Viết biểu thức biểu thị diện tích phần đất còn lại của mảnh vườn đó (lấy π = 3,14).

b) Tính diện tích phần đất còn lại của mảnh vườn đó biết x = 35, d = 4.

Lời giải

a) Chiều dài của mảnh vườn là x (m).

Chiều rộng bằng $\frac{3}{5}$ chiều dài nên chiều rộng của mảnh vườn là $\frac{3}{5}$x (m).

Biểu thức biểu thị diện tích của mảnh vườn hình chữ nhật là: x.$\frac{3}{5}$x  (m²).

Biểu thức biểu thị diện tích bể hình tròn đường kính d là: $\pi .{\left(\frac{d}{2}\right)}^2$ (m²).

Lấy π = 3,14 ta có diện tích bể hình tròn là 3,14 . ${\left(\frac{d}{2}\right)}^2$ (m²).

Khi đó biểu thức biểu thị diện tích phần đất còn lại của mảnh vườn đó là:

x.$\frac{3}{5}$x – 3,14 . ${\left(\frac{d}{2}\right)}^2$ (m²).

b) Thay x = 35, d = 4 vào biểu thức x.$\frac{3}{5}$x – 3,14 . ${\left(\frac{d}{2}\right)}^2$ ta được:

35.$\frac{3}{5}$.35 – 3,14 . ${\left(\frac{4}{2}\right)}^2$ = 735 – 3,14 . 4 = 722,44 (m²).

Vậy diện tích phần đất còn lại của mảnh vườn đó khi x = 35, d = 4 là 722,44 m².

Bài 9 trang 38 SBT Toán 7 Tập 1: 

Một khu vườn có dạng hình chữ nhật có chiều dài a (m), chiều rộng ngắn hơn chiều dài 8 (m). Trên khu vườn ấy, bác An đào một cái ao hình vuông có cạnh là b (m) (b < a – 8).

a) Viết biểu thức biểu thị diện tích còn lại của khu vườn đó.

b) Tính diện tích còn lại của khu vườn đó khi a = 50, b = 10.

Lời giải

a) Khu vườn hình chữ nhật có chiều dài a (m), chiều rộng ngắn hơn chiều dài 8 (m).

Khi đó chiều rộng của khu vườn là: a – 8 (m).

Biểu thức biểu thị diện tích khu vườn là: a . (a – 8) (m²).

Biểu thức biểu thị diện tích cái ao hình vuông cạnh b (m) là: b² (m²).

Vậy biểu thức biểu thị diện tích còn lại của khu vườn đó là:

a . (a – 8) – b² (m²).

b) Khi a = 50, b = 10 thay vào biểu thức a . (a – 8) – b² ta có:

50 . (50 – 8) – 10² = 50 . 42 – 100 = 2 000 (m²).

Vậy diện tích còn lại của khu vườn đó khi a = 50, b = 10 là 2 000 m².

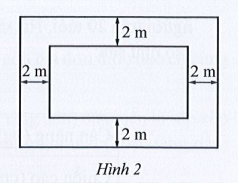
Bài 10 trang 39 SBT Toán 7 Tập 1: 

Trên mảnh đất có dạng hình chữ nhật với chiều dài là x (m), chiều rộng là y (m), người ta dự định làm một vườn hoa hình chữ nhật và bớt ra một phần đường đi rộng 2 m như ở Hình 2.

a) Viết biểu thức biểu thị chu vi và diện tích của vườn hoa trên mảnh đất đó.

b) Tính chu vi và diện tích của vườn hoa trên mảnh đất đó, biết x = 15, y = 10.

Lời giải

a) Chiều dài của vườn hoa trên mảnh đất đó là: x – 2 – 2 = x – 4 (m).

Chiều rộng của vườn hoa trên mảnh đất đó là: y – 2 – 2 = y – 4 (m).

Biểu thức biểu thị chu vi của vườn hoa trên mảnh đất đó là:

2[(x – 4) + (y – 4)] = 2(x + y – 8) (m).

Biểu thức biểu thị diện tích của vườn hoa trên mảnh đất đó là:

(x – 4)(y – 4) (m²).

b) Thay x = 15, y = 10 vào biểu thức biểu thị chu vi của vườn hoa ta có:

2 . (15 + 10 – 8) = 2 . 17 = 34 (m).

Thay x = 15, y = 10 vào biểu thức biểu thị diện tích của vườn hoa ta có:

(15 – 4) . (10 – 4) = 11 . 6 = 66 (m²).

Vậy khi x = 15, y = 10 thì chu vi và diện tích của vườn hoa lần lượt là 34 m và 66 m².

Bài 11 trang 39 SBT Toán 7 Tập 1: 

Viết biểu thức đại số biểu thị:

a) Khối lượng của một vật có thể tích V (m³) và khối lượng riêng D (kg/m³);

b) Diện tích của tam giác vuông có hai cạnh góc vuông là a (cm) và b (cm);

c) Sản lượng lúa thu hoạch được trên một ruộng lúa có diện tích là x (ha) và năng suất lúa là y (tạ/ha).

Lời giải

a) Biểu thức đại số biểu thị khối lượng của một vật có thể tích V (m³) và khối lượng riêng D (kg/m³) là V . D (kg).

b) Biểu thức đại số biểu thị diện tích của tam giác vuông có hai cạnh góc vuông là a (cm) và b (cm) là $\frac{1}{2}$ab (cm²).

c) Biểu thức đại số biểu thị sản lượng lúa thu hoạch được trên một ruộng lúa có diện tích là x (ha) và năng suất lúa là y (tạ/ha) là: xy (tạ).

Bài 12 trang 39 SBT Toán 7 Tập 1: 

Một ngôi nhà có ba phòng: sàn phòng khách có dạng hình vuông cạnh a (m), sàn phòng ngủ và sàn phòng bếp có dạng hình chữ nhật với cùng chiều dài a (m) và cùng chiều rộng b (m) (a > b). Viết biểu thức biểu thị tổng diện tích ba mặt sàn trên của ngôi nhà đó.

Lời giải

Biểu thức biểu thị diện tích mặt sàn phòng khách dạng hình vuông cạnh a (m) là a² (m²).

Biểu thức biểu thị diện tích mặt sàn phòng ngủ dạng hình chữ nhật chiều dài a (m) và chiều rộng b (m) là ab (m²).

Do sàn phòng ngủ và sàn phòng bếp có dạng hình chữ nhật có cùng kích thước nên diện tích mặt sàn phòng bếp là ab (m²).

Biểu thức biểu thị tổng diện tích ba mặt sàn trên của ngôi nhà đó là:

a² + ab + ab = a² + 2ab (m²).

Bài 13 trang 39 SBT Toán 7 Tập 1: 

Tính giá trị của mỗi biểu thức sau:

a) A = 3,2x²y³ tại x = 1, y = –1;

b) B = 3m – 2n tại m = –1, n = 2;

c) C = 7m + 2n – 5 tại m = –2, n = $-\frac{1}{2}$;

d) D = 3x² – 5y + 1 tại x = $\sqrt{3}$, y = –1.

Lời giải

a) Thay x = 1, y = –1 vào biểu thức A = 3,2x²y³ ta có:

A = 3,2 . 1² . (–1)³ = 3,2 . 1 . (–1) = –3,2.

Vậy với x = 1, y = –1 thì A = –3,2.

b) Thay m = –1, n = 2 vào biểu thức B = 3m – 2n ta có:

B = 3 . (–1) – 2 . 2 = – 3 – 4 = –7.

Vậy với m = –1, n = 2 thì B = –7.

c) Thay m = –2, n = $-\frac{1}{2}$ vào biểu thức C = 7m + 2n – 5 ta có:

C = 7 . (–2) + 2 . $\left(-\frac{1}{2}\right)$ – 5 = –14 – 1 – 5 = –20.

Vậy với m = –2, n = $-\frac{1}{2}$ thì C = –20.

d) Thay $x=\sqrt{3}$, y = –1 vào biểu thức D = 3x² – 5y + 1 ta có:

D = 3 . ${\left(\sqrt{3}\right)}^2$ – 5 . (–1) + 1 = 3 . 3 + 5 + 1 = 15.

Vậy với x = $\sqrt{3}$, y = –1 thì D = 15.

Bài 14* trang 39 SBT Toán 7 Tập 1: 

Tìm số nguyên x  để biểu thức:

a) A = $\frac{1}{50-x}$ (với x ≠ 50) đạt giá trị lớn nhất.

b) B = $\frac{4}{x-8}$ (với x ≠ 8) đạt giá trị nhỏ nhất.

Lời giải

a) Với x là số nguyên, x ≠ 50 ta xét hai trường hợp

• Trường hợp 1: Xét x ≤ 49, ta có 50 – x ≥ 1 > 0 nên A = $\frac{1}{50-x}$ > 0.

Biểu thức A có tử và mẫu đều dương, tử không đổi nên A lớn nhất nếu mẫu 50 − x là số nguyên dương nhỏ nhất, tức là 50 − x = 1.

Suy ra x = 49, khi đó A = 1.

• Trường hợp 2: Xét x ≥ 51, ta có 50 – x ≤ –1 < 0 nên A = $\frac{1}{50-x}$ < 0.

Khi đó A < 1 (mà 1 là giá trị lớn nhất của A ở trường hợp 1) nên trường hợp này không thể có giá trị của x để A lớn nhất.

Vậy với các số x nguyên (x ≠ 50) thì giá trị lớn nhất của A bằng 1 khi x = 49.

b) Với x là số nguyên, x ≠ 8 ta xét hai trường hợp:

• Trường hợp 1: Xét x ≤ 7, ta có x – 8 ≤ –1 < 0 nên B = $\frac{4}{x-8}$ < 0.

Số âm B có giá trị nhỏ nhất khi số đối của nó là lớn nhất.

Do đó $\frac{4}{-\left(x-8\right)}$ (với –(x – 8) ≥ 1 > 0) đạt giá trị lớn nhất.

Biểu thức trên có tử dương và mẫu dương nên đạt giá trị lớn nhất nếu mẫu –(x – 8) là số nguyên dương nhỏ nhất, tức là –(x – 8) = 1.

Suy ra x = 7, khi đó B = –4.

• Trường hợp 2: Xét x ≥ 9, ta có x – 8 ≥ 1 > 0 nên B = $\frac{4}{x-8}$ > 0.

Khi đó B > –4 (mà –4 là giá trị nhỏ nhất của B ở trường hợp 1) nên trường hợp này không thể có giá trị của x để B nhỏ nhất.

Vậy với các số x nguyên (x ≠ 8) thì giá trị nhỏ nhất của B là – 4 khi x = 7.

Bài 15 trang 39, 40 SBT Toán 7 Tập 1: 

Để đánh giá thể trạng của một người, người ta thường dùng chỉ số BMI. Chỉ số BMI được tính bằng công thức: $BMI=\frac{m}{h^2}$ (chỉ số này thường được làm tròn đến hàng phần mười) với m là cân nặng (tính theo ki-lô-gam) và h là chiều cao (tính theo mét). Nếu 18,5 ≤ BMI ≤ 22,9 thì được coi là thể trạng bình thường đối với người trên 20 tuổi. Hai chị Hằng và Bình (25 tuổi) có các số đo cân nặng và chiều cao như sau:

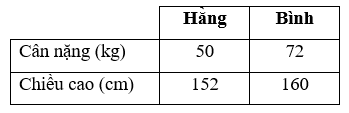
Trong hai chị Hằng và Bình, người nào đạt thể trạng bình thường?

Lời giải

Đổi 152 cm = 1,52 m;

       160 cm = 1,6 m.

Chỉ số BMI của chị Hằng là: $\frac{50}{{\mathrm{1,52}}^2}$ ≈ 21,6.

Chỉ số BMI của chị Bình là: $\frac{72}{{\mathrm{1,6}}^2}$ ≈ 28,1.

Ta có 18,5 ≤ 21,6 ≤ 22,9 và 28,1 > 22,9.

Do đó chị Hằng đạt thể trạng bình thường.

Vậy chị Hằng đạt thể trạng bình thường.

Bài 16 trang 40 SBT Toán 7 Tập 1: 

Bạn Nguyên đã mua 5 quyển vở, giá mỗi quyển là 7 000 đồng và mua x chiếc bút chì, giá mỗi chiếc là 4 000 đồng.

a) Viết biểu thức biểu thị số tiền bạn Nguyên phải trả.

b) Bạn Đức chỉ mua bút chì và mua nhiều hơn bạn Nguyên 5 chiếc bút chì cùng loại với giá 4 000 đồng/ chiếc. Viết biểu thức biểu thị số tiền bạn Đức phải trả.

Lời giải

a) Bạn Nguyên mua 5 quyển vở, giá mỗi quyển là 7 000 đồng nên phải trả số tiền là:

5 . 7 000 = 35 000 (đồng).

Bạn Nguyên mua x chiếc bút chì, giá mỗi chiếc là 4 000 đồng nên phải trả số tiền là:

4 000x (đồng).

Vậy biểu thức biểu thị số tiền bạn Nguyên phải trả là: 35 000 + 4 000x (đồng).

b) Số chiếc bút chì bạn Đức mua là: x + 5 (chiếc).

Số tiền bạn Đức phải trả khi mua x + 5 chiếc bút chì là:

4 000 . (x + 5) (đồng).

Vậy biểu thức biểu thị số tiền bạn Đức phải trả là 4 000 . (x + 5) (đồng).

Xem thêm lời giải sách bài tập Toán lớp 7 Cánh diều hay, chi tiết khác: 

Bài tập cuối chương 5

Bài 1. Biểu thức số. Biểu thức đại số

Bài 2. Đa thức một biến. Nghiệm của đa thức một biến

Bài 3. Phép cộng, phép trừ đa thức một biến

Bài 4. Phép nhân đa thức một biến