Nội dung bài viết

    Xem thêm

    Sách bài tập Toán 7 Bài 3 (Cánh diều): Hai tam giác bằng nhau 

    Với giải sách bài tập Toán 7 Bài 3. Hai tam giác bằng nhau sách Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập trong SBT Toán 7 Bài 3.

    1 1,126 01/01/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Giải sách bài tập Toán 7 Bài 3. Hai tam giác bằng nhau

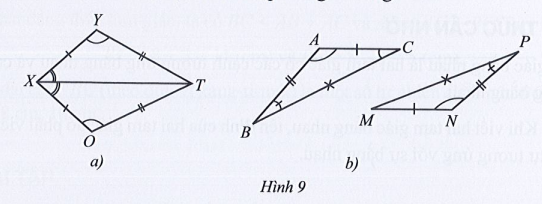
    Bài 19 trang 72 SBT Toán 7 Tập 2: Quan sát các hình 9a, 9b, viết các cặp tam giác bằng nhau.

    Sách bài tập Toán 7 Bài 3 (Cánh diều): Hai tam giác bằng nhau  (ảnh 1) 

    Lời giải

    Hình a)

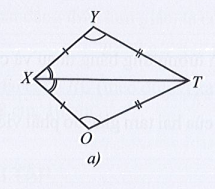
    Sách bài tập Toán 7 Bài 3 (Cánh diều): Hai tam giác bằng nhau  (ảnh 1) 

     Xét tam giác XYT và tam giác XOT có:

    +) XY = XO, YT = OT, XT là cạnh chung;

    +) TXY^=TXO^,  Y^=O^,  XTY^=OTX^.

    Do đó ∆XYT = ∆XOT.

    Vậy ∆XYT = ∆XOT.

    Hình b)

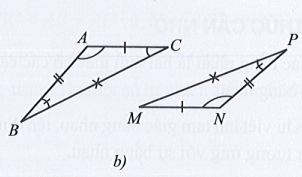
    Sách bài tập Toán 7 Bài 3 (Cánh diều): Hai tam giác bằng nhau  (ảnh 1) 

    Xét tam giác ABC và tam giác NPM có:

    +) AB = NP, BC = PM, AC = NM;

    +) A^=N^,  B^=P^,  C^=M^.

    Do đó ∆ABC = ∆NPM.

    Vậy ∆ABC = ∆NPM.

    Bài 20 trang 72 SBT Toán 7 Tập 2: Cho hai tam giác bằng nhau: tam giác ABC và một tam giác có ba đỉnh là X, Y, Z. Viết kí hiệu sự bằng nhau của hai tam giác đó trong mỗi trường hợp sau:

    a) A^=X^,  B^=Z^;

    b) AB = XY, BC = YZ.

    Lời giải

    Vì tam giác ABC và tam giác có ba đỉnh X, Y, Z bằng nhau nên để viết được kí hiệu sự bằng nhau của hai tam giác đó, ta sẽ tìm các đỉnh tương ứng của hai tam giác này.

    a) Do A^=X^,  B^=Z^ nên đỉnh A tương ứng với đỉnh X, đỉnh B tương ứng với đỉnh Z.

    Khi đó đỉnh C tương ứng với đỉnh Y.

    Do đó kí hiệu sự bằng nhau của hai tam giác này là ∆ABC = ∆XZY.

    Vậy ∆ABC = ∆XZY.

    b) Ta có AB = XY, BC = YZ nên đỉnh B tương ứng với đỉnh Y.

    Khi đó đỉnh A tương ứng với đỉnh X và đỉnh C tương tứng với đỉnh Z.

    Do đó kí hiệu sự bằng nhau của hai tam giác này là ∆ABC = ∆XYZ.

    Vậy ∆ABC = ∆XYZ.

    Bài 21 trang 72 SBT Toán 7 Tập 2: Bạn Sơn cho rằng “Nếu độ dài các cạnh của tam giác ABC đều là số tự nhiên và ∆ABC = ∆MNP thì tổng chu vi của tam giác ABC và tam giác MNP là số lẻ”. Bạn Sơn nói như vậy có đúng không? Vì sao?

    Lời giải

    Vì ∆ABC = ∆MNP nên AB = MN, BC = NP, AC = MP (các cặp cạnh tương ứng).

    Suy ra AB + BC + AC = MN + NP + MP.

    Hay chu vi của tam giác MNP bằng chu vi của tam giác ABC.

    Do độ dài các cạnh của tam giác ABC đều là số tự nhiên nên chu vi của tam giác ABC cũng là số tự nhiên.

    Gọi chu vi của tam giác ABC là x (x là số tự nhiên).

    Khi đó, chu vi của tam giác MNP là x.

    Do đó, tổng chu vi của tam giác ABC và tam giác MNP là:

    x + x = 2x (là số chẵn).

    Vậy bạn Sơn nói không đúng.

    Bài 22 trang 73 SBT Toán 7 Tập 2 : Cho ∆ABC = ∆DEG có AB = 4 dm, BC = 7 dm, CA = 9,5 dm. Tính chu vi của tma giác DEG.

    Lời giải

    Vì ∆ ABC = ∆ DEG nên ta có: AB = DE, BC = EG, AC = DG (các cặp cạnh tương ứng).

    Do đó chu vi của tam giác DEG bằng chu vi của tam giác ABC.

    Mà chu vi tam giác ABC là: 4 + 7 + 9,5 = 20,5 (dm).

    Do đó chu vi tam giác DEG bằng 20,5 dm.

    Vậy chu vi tam giác DEG bằng 20,5 dm.

    Bài 23 trang 73 SBT Toán 7 Tập 2 : Cho ∆ABC = ∆GIK có số đo G^,  I^,  K^ tỉ lệ với 2; 3; 4. Tính số đo mỗi góc của tam giác ABC.

    Lời giải

    Vì số đo G^,  I^,  K^ tỉ lệ với 2; 3; 4 nên ta có: G^2=I^3=K^4.

    Xét ∆GIK có G^+I^+K^=180o (tổng ba góc của một tam giác).

    Áp dụng tính chất dãy tỉ số bằng nhau ta có:

    G^2=I^3=K^4=G^+I^+K^9=180°9=20° 

    Suy ra

    • G^=2.20°=40°;

    • I^=3.20°=60°;

    • K^=4.20°=80°.

    Do ∆ABC = ∆GIK nên A^=G^,  B^=I^,  C^=K^ (các cặp góc tương ứng).

    Mà G^=40°,  I^=60°,  K^=80° 

    Suy ra A^=40°, B^=60°, C^=80°.

    Vậy A^=40°,B^=60°,C^=80°.

    Bài 24 trang 73 SBT Toán 7 Tập 2: Cho ∆ABC = ∆XYZ có 3BC = 5AB, YZ – XY = 10 cm và AC = 35 cm. Tính độ dài mỗi cạnh của tam giác XYZ.

    Lời giải

    Do ∆ABC = ∆XYZ (giả thiết)

    Nên AB = XY, BC = YZ, AC = XZ (các cặp cạnh tương ứng)

    Mà AC = 35 cm nên XZ = 35 cm.

    Ta có YZ – XY = 10 (cm) suy ra BC – AB = 10 (cm).

    Hay BC = AB + 10.

    Mà 3BC = 5AB

    Suy ra 3(AB + 10) = 5AB

    Hay 5AB – 3AB = 30

    Do đó 2AB = 30

    Suy ra AB = 15 (cm) 

    Khi đó BC = 25 (cm)

    Lại có AB = XY, BC = YZ nên XY = 15 (cm) và YZ = 25 (cm).

    Vậy XY = 15 cm, YZ = 25 cm, XZ = 35 cm.

    Bài 25 trang 73 SBT Toán 7 Tập 2: 

    Cho ∆ABC = ∆XYZ, có A^+Y^=120° và A^−Y^=40°. Tính số đo mỗi góc của từng tam giác trên.

    Lời giải

    Do A^+Y^=120° và A^−Y^=40° nên 2A^=120°+40°=160° 

    Suy ra A^=160°:2=80°

    Do đó Y^=120°−A^=120°−80°=40°

    Vì ∆ABC = ∆XYZ (giả thiết)

    Nên  A^=X^,  B^=Y^, C^=Z^ (các cặp góc tương ứng).

    Mà A^=80°,Y^=40°

    Suy ra X^=80°,B^=40°

    Xét ∆ABC có: C^+B^+A^=180° (tổng ba góc của một tam giác).

    Do đó C^=180°−B^−A^=180°−40°−80°=60°

    Suy ra Z^=60°.

    Vậy A^=80°,B^=40°,C^=60°,X^=80°,Y^=40°,Z^=60°.

    Bài 26 trang 73 SBT Toán 7 Tập 2: Cho ∆ABC  = ∆MNP. Hai tia phân giác của góc B và C cắt nhau tại O tạo thành góc BOC bằng 120°. Tính tổng số đo các góc MNP và MPN của tam giác MNP.

    Lời giải

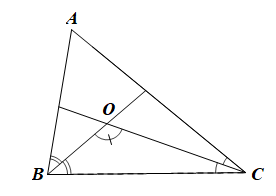
    Sách bài tập Toán 7 Bài 3 (Cánh diều): Hai tam giác bằng nhau  (ảnh 1) 

    Vì BO là phân giác của góc ABC nên ABO^=CBO^=ABC^2

    Vì CO là phân giác của góc ACB nên ACO^=BCO^=ACB^2

    Xét ∆COB ta có: BOC^+OBC^+OCB^=180° (tổng ba góc của một tam giác).

    Suy ra OBC^+OCB^=180°−BOC^=180°−120°=60°.

    Mà CBO^=ABC^2, BCO^=ACB^2. 

    Suy ra ABC^2+ACB^2=60°

    Do đó ABC^+ACB^=2.60°=120°.

    Mặt khác ∆ABC  = ∆MNP nên ta có:

    ABC^=MNP^ và ACB^=MPN^(các cặp góc tương ứng).

    Suy ra MNP^+MPN^=ABC^+ACB^=120°

    Vậy MNP^+MPN^=120°.

    Xem thêm lời giải sách bài tập Toán lớp 7 Cánh diều hay, chi tiết khác: 

    Bài 2. Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác

    Bài 3. Hai tam giác bằng nhau

    Bài 4. Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh

    Bài 5. Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh

    Bài 6. Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc

    Tham khảo các loạt bài Toán 7 khác:

    Bài viết cùng lớp mới nhất

    Xem thêm
    1 1,126 01/01/2023
    Trang trước
    Chia sẻ
    Trang sau  

    Xem thêm các chương trình khác: