Sách bài tập Toán 7 (Cánh diều): Bài tập cuối chương 6 

Giải sách bài tập Toán 7 Bài tập cuối chương 6

Bài 50 trang 55 SBT Toán 7 Tập 1: 

Giá trị của biểu thức (x² – 8)(x + 3) – (x – 2)(x + 5) tại x = 3 là:

A. – 2

B. 16

C. – 10

D. 10

Lời giải

Đáp án đúng là: A

Thay x = 3 vào biểu thức (x² – 8)(x + 3) – (x – 2)(x + 5) ta được:

(3² – 8)(3 + 3) – (3 – 2)(3 + 5) = 1 . 6 – 1 . 8 = –2.

Vậy ta chọn phương án A.

Bài 51 trang 55 SBT Toán 7 Tập 1: 

Biểu thức nào sau đây là đa thức một biến? Tìm biến và bậc của đa thức đó.

a) – 2 022x;

b) – 6x² – 4x + 2;

c) 3uⁿ – 8u² – 20 (n ∈ ℕ, n > 2);  

d) $\frac{1}{x}+x^3-2x^2+1$.

Lời giải

a) Biểu thức –2 022x là một đa thức một biến x.

Đa thức này có bậc là 1.

b) Biểu thức – 6x² – 4x + 2 là một đa thức một biến x.

Đa thức này có bậc là 2.

c) Biểu thức 3uⁿ – 8u² – 20 (n ∈ ℕ, n > 2) là một đa thức một biến u.

Đa thức này có bậc là n với n ∈ ℕ, n > 2.

d) Biểu thức $\frac{1}{x}+x^3-2x^2+1$ không phải là một đa thức một biến x.

Bài 52 trang 55 SBT Toán 7 Tập 1: Tính giá trị của biểu thức:

a) A = 56 – 5a + 6b tại a = 22, b = 23;

b) B = 6xyz – 3xy – 19z tại x = 11, y = 32, z = 0;

c) C = x²⁰²¹y – 2 022x² + 2 023y³ + 7 tại x = –1 và y = 1;

d) D = x⁴ – 17x³ + 17x² – 17x + 21 tại x = 16.

Lời giải

a) Thay a = 22, b = 23 vào A = 56 – 5a + 6b ta có:

A = 56 – 5 . 22 + 6 . 23 = 56 – 110 + 138 = 84.

Vậy tại a = 22, b = 23 thì biểu thức A có giá trị bằng 84.

b) Thay x = 11, y = 32, z = 0 vào B = 6xyz – 3xy – 19z ta có:

B = 6 . 11 . 32 . 0 – 3 . 11 . 32 – 19 . 0

   = 0 – 1 056 – 0 = –1 056.

Vậy tại x = 11, y = 32, z = 0 thì biểu thức B có giá trị bằng –1 056.

c) Thay x = –1 và y = 1 vào C = x²⁰²¹y – 2 022x² + 2 023y³ + 7 ta có:

C = (–1)²⁰²¹ . 1 – 2 022 . (–1)² + 2 023 . 1³ + 7

   = –1 – 2 022 + 2023 + 7 = 7.

Vậy tại x = –1 và y = 1 thì biểu thức C có giá trị bằng 7.

d) Với x = 16 ta có x + 1 = 17.

Khi đó ta có:

D = x⁴ – 17x³ + 17x² – 17x + 21

    = x⁴ – (x + 1) . x³ + (x + 1) . x² – (x + 1) . x + 21

    = x⁴ – x⁴ – x³ + x³ + x² – x² – x + 21

    = – x + 21

Thay x = 16 vào D = – x + 21 ta có:

D = – 16 + 21 = 5.

Vậy tại x = 16 thì biểu thức D có giá trị bằng 5.

Bài 53 trang 55 SBT Toán 7 Tập 1: Một bể đang chứa 500 l nước. Người ta mở một vòi nước cho chảy vào bể đó, mỗi phút vòi nước đó chảy vào bể được 50 l nước. Viết biểu thức biểu thị lượng nước có trong bể sau khi đã mở vòi nước đó được x phút, biết rằng sau x phút bể nước đó chưa đầy.

Lời giải

Mỗi phút vòi nước đó chảy vào bể được 50 l nước thì sau x phút vòi nước đó chảy vào bể được 50x (l nước).

Bể đang chứa 500 l nước, chảy thêm được 50x (l nước) thì sau x phút, lượng nước trong bể có là 500 + 50x (l nước).

Bài 54 trang 55 SBT Toán 7 Tập 1: Viết đa thức biến x trong mỗi trường hợp sau:

a) Đa thức bậc nhất có hệ số của biến bằng – 7 và hệ số tự do bằng 0.

b) Đa thức bậc ba có hệ số của lũy thừa bậc hai và bậc nhất của biến đều bằng 5.

c) Đa thức bậc bốn có tổng hệ số của lũy thừa bậc ba và bậc hai của biến bằng 6 và hệ số tự do bằng – 1.

d) Đa thức bậc tám trong đó tất cả các hệ số của lũy thừa bậc lẻ của biến đều bằng 0.

Lời giải

a) Gọi đa thức bậc nhất biến x cần tìm có dạng ax + b (a ≠ 0).

Đa thức trên có:

• Hệ số của biến bằng – 7 nên a = – 7.

• Hệ số tự do bằng 0 nên b = 0.

Vậy đa thức biến x cần tìm là –7x.

b) Gọi đa thức bậc ba biến x cần tìm có dạng ax³ + bx² + cx + d (a ≠ 0).

Đa thức trên có:

• Hệ số của lũy thừa bậc hai bằng 5 nên b = 5;

• Hệ số của lũy thừa bậc nhấ bằng 5 nên c = 5;

Vậy đa thức biến x cần tìm là ax³ + 5x² + 5x + d (a ≠ 0).

c) Gọi đa thức bậc bốn biến x cần tìm có dạng ax⁴ + bx³ + cx² + dx + e (a ≠ 0).

Đa thức trên có:

• Tổng hệ số của lũy thừa bậc ba và bậc hai của biến bằng 6 nên b + c = 6.

Do đó c = 6 – b.

• Hệ số tự do bằng – 1 nên e = – 1.

Vậy đa thức biến x cần tìm là ax⁴ + bx³ + (6 – b)x² + dx – 1 (a ≠ 0).

d) Đa thức bậc tám biến x trong đó tất cả các hệ số của lũy thừa bậc lẻ của biến đều bằng 0 là: ax⁸ + bx⁶ + cx⁴ + dx² + e (a ≠ 0).

Bài 55* trang 55 SBT Toán 7 Tập 1: 

Tìm giá trị của m để đa thức sau là đa thức bậc ba theo biến x:

P(x) = (m² – 25)x⁴ + (20 + 4m)x³  +17x² – 23.

Lời giải

Đa thức P(x) là đa thức bậc ba khi và chỉ khi:

m² – 25 = 0 (1) và 20 + 4m ≠ 0 (2)

• Giải (2):

20 + 4m ≠ 0

4m ≠ –20

m ≠ –5

• Giải (1):

m² – 25 = 0

m² = 25

m² = 5² = (–5)²

m = 5 (thỏa mãn m ≠ –5) hoặc m = –5 (không thỏa mãn m ≠ –5).

Vậy với m = 5 thì đa thức P(x) đã cho là đa thức bậc ba.

Bài 56 trang 55 SBT Toán 7 Tập 1: 

Cho đa thức A(x) = – 11x⁵ + 4x³ – 12x² + 11x⁵ + 13x² – 7x + 2.

a) Thu gọn và sắp xếp đa thức A(x) theo số mũ giảm dần của biến.

b) Tìm bậc của đa thức A(x).

c) Tính giá trị của đa thức A(x) tại x = –1; x = 0; x = 2.

Lời giải

a) A(x) = – 11x⁵ + 4x³ – 12x² + 11x⁵ + 13x² – 7x + 2.

             = (– 11x⁵ + 11x⁵) + 4x³ + (– 12x² + 13x²) – 7x + 2.

             = 4x³ + x² – 7x + 2.

Vậy A(x) = 4x³ + x² – 7x + 2.

b) Đa thức A(x) = 4x³ + x² – 7x + 2 có bậc là 3 do số mũ lớn nhất của biến x là 3.

c) Xét đa thức A(x) = 4x³ + x² – 7x + 2.

• Tại x = –1 ta có:

A(–1) = 4 . (–1)³ + (–1)² – 7 . (–1) + 2

           = –4 + 1 + 7 + 2 = 6.

• Tại x = 0 ta có:

A(0) = 4 . 0³ + 0² – 7 . 0 + 2

           = 0 + 0 – 0 + 2 = 2.

• Tại x = 2 ta có:

A(2) = 4 . 2³ + 2² – 7 . 2 + 2

           = 32 + 4 – 14 + 2 = 24.

Vậy A(–1) = 6; A(0) = 2 và A(2) = 24.

Bài 57 trang 56 SBT Toán 7 Tập 1: 

Tính:

a) (– 4x³ – 13x² + 2x⁵) + (13x² + 2x³ – 12x – 1);

b) (12x⁶ – 11x² + 3x³ + 9) – (13x⁶ + 2x³ – 11x² – 11x);

c) (8x³ – x² + 1)(x² – 1);

d) (8x³ + 6x² + 3x + 1) : (2x + 1).

Lời giải

a) (– 4x³ – 13x² + 2x⁵) + (13x² + 2x³ – 12x – 1)

= – 4x³ – 13x² + 2x⁵ + 13x² + 2x³ – 12x – 1

= 2x⁵ + (– 4x³ + 2x³) + (– 13x² + 13x²) – 12x – 1

= 2x⁵ – 2x³ – 12x – 1.

b) (12x⁶ – 11x² + 3x³ + 9) – (13x⁶ + 2x³ – 11x² – 11x)

= 12x⁶ – 11x² + 3x³ + 9 – 13x⁶ – 2x³ + 11x² + 11x

= (12x⁶ – 13x⁶) + (3x³ – 2x³) + (– 11x² + 11x²) + 11x + 9

= – x⁶ + x³ + 11x + 9.

c) (8x³ – x² + 1)(x² – 1)

= 8x³ . (x² – 1) – x² . (x² – 1) + (x² – 1)

= 8x⁵ – 8x³ – x⁴ + x² + x² – 1

= 8x⁵ – x⁴ – 8x³ + 2x² – 1.

d) (8x³ + 6x² + 3x + 1) : (2x + 1)

Ta thực hiện đặt tính chia đa thức như sau:

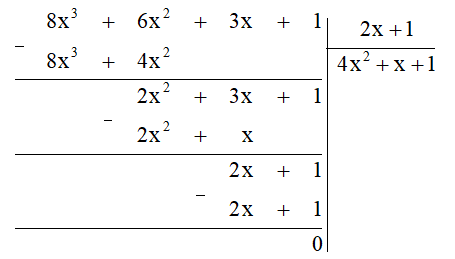
Vậy (8x³ + 6x² + 3x + 1) : (2x + 1) = 4x² + x + 1.

Bài 58 trang 56 SBT Toán 7 Tập 1: 

Tìm đa thức C(x) sao cho A(x) – C(x) = B(x), biết:

a) A(x) = x³ + x² + x – 2, B(x) = 9 – 2x + 11x³ + x⁴.

b) A(x) = – 12x⁵ + 2x³ – 2, B(x) = 9 – 2x – 11x² + 2x³ – 11x⁵.

Lời giải

Ta có A(x) – C(x) = B(x)

Suy ra C(x) = A(x) – B(x)

a) Với A(x) = x³ + x² + x – 2, B(x) = 9 – 2x + 11x³ + x⁴ ta có:

C(x) = (x³ + x² + x – 2) – (9 – 2x + 11x³ + x⁴)

        = x³ + x² + x – 2 – 9 + 2x – 11x³ – x⁴

        = – x⁴ + (x³ – 11x³) + x² + (x + 2x) – 2 – 9

        = – x⁴ – 10x³ + x² + 3x – 11.

b) Với A(x) = –12x⁵ + 2x³ – 2, B(x) = 9 – 2x – 11x² + 2x³ – 11x⁵ ta có:

C(x) = (– 12x⁵ + 2x³ – 2) – (9 – 2x – 11x² + 2x³ – 11x⁵)

         = – 12x⁵ + 2x³ – 2 – 9 + 2x + 11x² – 2x³ + 11x⁵

         = (– 12x⁵ + 11x⁵) + (2x³ – 2x³) + 11x² + 2x – 2 – 9

         = – x⁵ + 11x² + 2x – 11.

Bài 59 trang 56 SBT Toán 7 Tập 1: 

Tìm đa thức Q(x) sao cho P(x).Q(x) = R(x), biết:

a) P(x) = x – 2, R(x) = –x³ + 8;

b) P(x) = x² – 3x + 2, R(x) = 10 – 13x + 2x² + x³.

Lời giải

Ta có P(x).Q(x) = R(x)

Suy ra Q(x) = R(x) : P(x).

a) Với P(x) = x – 2, R(x) = –x³ + 8 ta có:

Q(x) = (–x³ + 8) : (x – 2)

Ta thực hiện đặt tính chia đa thức như sau:

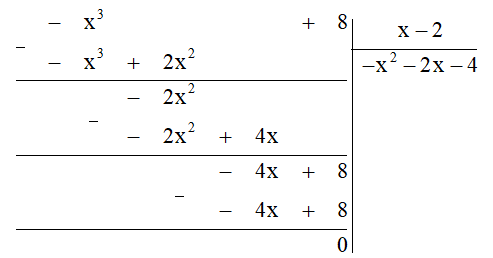
Khi đó Q(x) = (–x³ + 8) : (x – 2) = – x² – 2x – 4.

Vậy Q(x) = – x² – 2x – 4.

b) Với P(x) = x² – 3x + 2, R(x) = 10 – 13x + 2x² + x³ ta có:

Q(x) = (10 – 13x + 2x² + x³) : (x² – 3x + 2)

         = (x³ + 2x² – 13x + 10) : (x² – 3x + 2)

Ta thực hiện đặt tính chia đa thức như sau:

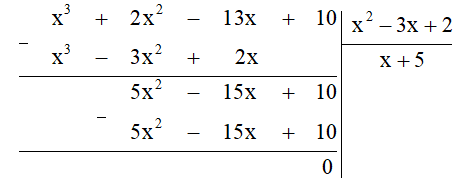
Khi đó Q(x) = (x³ + 2x² – 13x + 10) : (x² – 3x + 2) = x + 5.

Vậy Q(x) = x + 5.

Bài 60 trang 56 SBT Toán 7 Tập 1: 

Tìm hệ số a sao cho đa thức G(x) = x⁴ + x² + a chia hết cho đa thức M(x) = x² – x + 1.

Lời giải

Ta thực hiện đặt tính chia đa thức như sau:

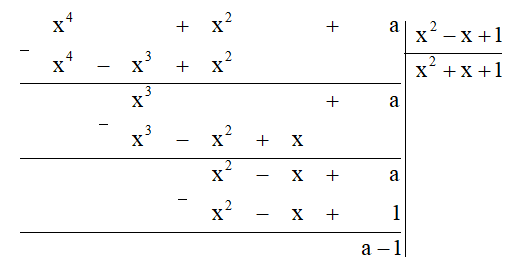
Do đó G(x) : M(x) = x² + x + 1 (dư a – 1).

Để đa thức G(x) chia hết cho đa thức M(x) thì số dư phải bằng 0.

Tức là a – 1 = 0, hay a = 1.

Vậy a = 1 thì đa thức G(x) = x⁴ + x² + a chia hết cho đa thức M(x) = x² – x + 1.

Bài 61 trang 56 SBT Toán 7 Tập 1: 

Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?

a) x = 2 và x = –3 là nghiệm của đa thức P(x) = x² – 5x + 6.

b) Đa thức bậc bốn luôn có nhiều hơn bốn nghiệm.

c) Mỗi phần tử của tập hợp {0; 1; –1} là nghiệm của đa thức P(x) = x³ – x.

Lời giải

a) Xét đa thức P(x) = x² – 5x + 6.

• Tại x = 2 ta có:

P(2) = 2² – 5 . 2 + 6 = 4 – 10 + 6 = 0.

Do đó x = 2 là một nghiệm của đa thức P(x).

• Tại x = –3 ta có:

P(–3) = (–3)² – 5 . (–3) + 6 = 9 + 15 + 6 = 30.

Do đó x = –3 không là nghiệm của đa thức P(x).

Vậy phát biểu a) là sai.

b) Đa thức bậc bốn có nhiều nhất là bốn nghiệm. Do đó phát biểu b) là sai.

c) Xét đa thức P(x) = x³ – x.

• Tại x = 0 ta có:

P(0) = 0³ – 0 = 0.

Do đó x = 0 là một nghiệm của đa thức P(x).

• Tại x = 1 ta có:

P(1) = 1³ – 1 = 0.

Do đó x = 1 là một nghiệm của đa thức P(x).

• Tại x = –1 ta có:

P(–1) = (–1)³ – (–1) = –1 + 1 = 0.

Do đó x = –1là một nghiệm của đa thức P(x).

Vậy phát biểu c) là đúng.

Bài 62 trang 56 SBT Toán 7 Tập 1: 

Cho đa thức P(x) = ax⁴ + bx³ + cx² + dx + e (a ≠ 0) với a + b + c + d + e = 0. Chứng tỏ rằng x = 1 là nghiệm của đa thức P(x).

Lời giải

Xét đa thức P(x) = ax⁴ + bx³ + cx² + dx + e (a ≠ 0).

Tại x = 1 ta có:

P(1) = a . 1⁴ + b . 1³ + c . 1² + d . 1 + e

        = a + b + c + d + e

        = 0                (do a + b + c + d + e = 0).

Do đó x = 1 là nghiệm của đa thức P(x).

Vậy x = 1 là nghiệm của đa thức P(x).

Bài 63 trang 56 SBT Toán 7 Tập 1: 

Cho đa thức Q(x) = ax² + bx + c (a ≠ 0). Chứng minh rằng nếu Q(x) nhận 1 và –1 là nghiệm thì a và c là hai số đối nhau.

Lời giải

Xét đa thức Q(x) = ax² + bx + c (a ≠ 0).

• Tại x = 1 ta có:

Q(1) = a . 1² + b . 1 + c = a + b + c.

Theo bài Q(x) nhận 1 là nghiệm nên Q(1) = 0.

Do đó a + b + c = 0 (1).

• Tại x = –1 ta có:

Q(–1) = a . (–1)² + b . (–1) + c = a – b + c.

Theo bài Q(x) nhận –1 là nghiệm nên Q(–1) = 0.

Do đó a – b + c = 0 (2)

• Cộng vế theo vế của (1) và (2) ta được:

(a + b + c) + (a – b + c) = 0

a + b + c + a – b + c = 0

2a + 2c = 0

a + c = 0

a = – c.

Do đó a và c là hai số đối nhau.

Vậy a và c là hai số đối nhau.

Bài 64 trang 56 SBT Toán 7 Tập 1: 

Một cửa hàng bán hoa sau khi tăng giá 50 nghìn đồng mỗi chậu hoa so với giá bán ban đầu là 3x (nghìn đồng) thì số tiền thu được là 3x² + 53x + 50 (nghìn đồng). Tính số chậu hoa mà cửa hàng đã bán theo x.

Lời giải

Giá một chậu hoa sau khi tăng giá 50 nghìn đồng mỗi chậu so với giá bán ban đầu là 3x (nghìn đồng) là: 3x + 50 (nghìn đồng).

Số chậu hoa mà cửa hàng đã bán được là thương của phép chia đa thức:

(3x² + 53x + 50) : (3x + 50).

Ta thực hiện đặt tính chia đa thức như sau:

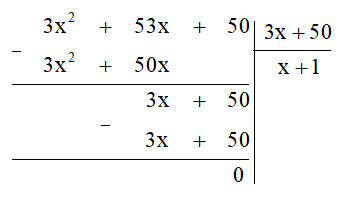
Khi đó ta có (3x² + 53x + 50) : (3x + 50) = x + 1.

Vậy số chậu hoa mà cửa hàng đã bán là x + 1 (chậu hoa).

Bài 65 trang 56, 57 SBT Toán 7 Tập 1: 

Tháng 5 năm 2019, nhiều đại biểu trên cả nước đã “hội quân” trên một tàu kiểm ngư rời cảng biển quốc tế Cam Ranh để bắt đầu hải trình nối tình yêu đất liền với biển đảo Trường Sa. Do thời tiết xấu, tàu kiểm ngư đã giảm 15% tốc độ so với tốc độ đã định. Giả sử tốc độ đã định của tàu kiểm ngư là x hải lí/giờ. Viết biểu thức biểu thị số hải lí mà tàu kiểm ngư đã đi với số thời gian:

a) 1 giờ;

b) 4 giờ;

c) y giờ.

Lời giải

Tốc độ thực tế tàu kiểm như đã đi bằng 100% – 15% = 85% so với tốc độ đã định và bằng 85%.x = 0,85x (hải lí/giờ).

a) Biểu thức biểu thị số hải lí mà tàu kiểm ngư đã đi trong 1 giờ là:

0,85x . 1 = 0,85x (hải lí).

b) Biểu thức biểu thị số hải lí mà tàu kiểm ngư đã đi trong 4 giờ là:

0,85x . 4 = 3,4x (hải lí).

c) Biểu thức biểu thị số hải lí mà tàu kiểm ngư đã đi trong 1 giờ là:

0,85x . y = 0,85xy (hải lí).

Bài 66 trang 57 SBT Toán 7 Tập 1: 

Lượng khí thải gây hiệu ứng nhà kính do các hoạt động của con người là nguyên nhân gây ra nhiệt độ Trái Đất tăng một cách đáng kể. Các nhà khoa học đưa ra biểu thức dự báo nhiệt độ trung bình trên bề mặt Trái Đất như sau: T = 0,02x + 15. Trong đó, T là nhiệt độ trung bình của bề mặt Trái Đất tính theo độ C, x là số năm kể từ năm 1960. Tính nhiệt độ trung bình của bề mặt Trái Đất vào các năm 1965 và năm 2023 theo biểu thức dự báo trên.

Lời giải

Nhiệt độ trung bình của bề mặt Trái Đất vào năm 1965 là:

T = 0,02 . (1 965 – 1 960) + 15 = 15,1 (°C).

Nhiệt độ trung bình của bề mặt Trái Đất vào năm 2023 là:

T = 0,02 . (2 023 – 1 960) + 15 = 16,26 (°C).

Bài 67 trang 57 SBT Toán 7 Tập 1: 

Giá bán lẻ 1 hộp sữa là 7 000 đồng, giá cho 1 lốc sữa 4 hộp là 26 000 đồng. Nếu mua từ 4 lốc sữa trở lên thì cứ 2 lốc sữa được tặng 1 hộp. Vậy nếu bác Hoa mua 2a (a ∈ ℕ, 2 ≤ a < 10) lốc sữa thì sẽ tiết kiệm bao nhiêu tiền so với mua lẻ từng hộp?

Lời giải

Do nếu mua từ 4 lốc sữa trở lên thì cứ mua 2 lốc sữa được tặng 1 hộp nên mua 2a lốc sữa được tặng a hộp.

Số tiền bác Hoa mua 2a lốc sữa là:

26 000 . 2a = 52 000a (đồng).

Tổng số hộp sữa bác Hoa nhận được là:

2a . 4 + a = 8a + a = 9a (hộp).

Số tiền bác Hoa phải trả nếu mua lẻ từng hộp số sữa trên là:

9a . 7 000 = 63 000a (đồng).

Số tiền bác Hoa sẽ tiết kiệm là:

63 000a – 52 000a = 11 000a (đồng).

Vậy bác Hoa sẽ tiết kiệm được 11 000a đồng so với mua lẻ từng hộp.

Bài 68 trang 57 SBT Toán 7 Tập 1: 

Nhân dịp cuối năm, một cửa hàng cần thanh lí một lô hàng (gồm 100 sản phẩm cùng loại) với giá bán là x đồng/chiếc. Lần đầu cửa hàng giảm 10% so với giá bán thì bán được 15 sản phẩm, lần sau cửa hàng giảm thêm 5% nữa (so với giá đã giảm lần đầu) thì bán được hết 85 sản phẩm còn lại. Viết biểu thức biểu thị số tiền cửa hàng thu được sau khi đã bán hết 100 sản phẩm trên.

Lời giải

Lần đầu cửa hàng giảm 10% so với giá bán nên giá tiền của mỗi sản phẩm bán ra sau lần giảm giá đầu tiên bằng 100% – 10% = 90% giá bán ban đầu và bằng:

90%x = 0,9x (đồng).

Số tiền cửa hàng thu được sau lần đầu giảm giá là:

0,9x . 15 = 13,5x (đồng).

Lần sau cửa hàng giảm thêm 5% nữa (so với giá đã giảm lần đầu) nên giá tiền của mỗi sản phẩm bán lần ra sau lần giảm giá thứ hai bằng 100% – 5% = 95% giá bán ra sau lần giảm giá đầu tiên và bằng:

95% . 0,9x = 0,95 . 0,9x = 0,855x (đồng).

Số tiền cửa hàng thu được khi bán hết 85 sản phẩm còn lại là:

0,855x . 85 = 72,675x (đồng).

Số tiền cửa hàng thu được sau khi đã bán hết 100 sản phẩm trên là:

13,5x + 72,675x =  86,175x (đồng).

Vậy biểu thức biểu thị số tiền cửa hàng thu được sau khi đã bán hết 100 sản phẩm trên là: 86,175x (đồng).

Bài 69 trang 57 SBT Toán 7 Tập 1: 

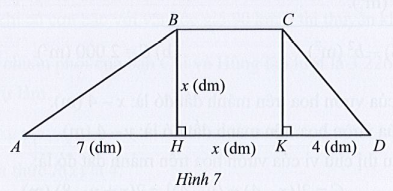
Tính diện tích của hình thang ABCD với các số đo cho như Hình 7 theo x.

 

Lời giải

Diện tích hình tam giác vuông ABH là: S_ABH = $\frac{1}{2}$.x.7 = $\frac{7}{2}$x (dm²).

Diện tích hình vuông BCKH là: S_BCKH = x² (dm²).

Diện tích tam giác vuông CDK là: S_CDK = $\frac{1}{2}$x.4 = 2x (dm²).

Diện tích hình thang ABCD là:

S_ABCD = S_ABH + S_BCKH + S_CDK 

           = $\frac{7}{2}$x + x² + 2x

           = x² + $\frac{11}{2}$x (dm²).

Vậy diện tích hình thang ABCD là x² + $\frac{11}{2}$x (dm²).

Xem thêm lời giải sách bài tập Toán lớp 7 Cánh diều hay, chi tiết khác: 

Bài 5. Phép chia đa thức một biến

Bài tập cuối chương 6

Bài 1. Tổng các góc của một tam giác

Bài 2. Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác

Bài 3. Hai tam giác bằng nhau