Lý thuyết Bài ôn tập chương 3 chi tiết – Toán lớp 6 Kết nối tri thức
Với lý thuyết Toán lớp 6 Bài ôn tập chương 3 chi tiết, ngắn gọn và bài tập tự luyện có lời giải chi tiết sách Kết nối tri thức sẽ giúp học sinh nắm vững kiến thức trọng tâm để học tốt môn Toán 6.
A. Lý thuyết Toán 6 Bài ôn tập chương 3 – Kết nối tri thức
I. Tập hợp các số nguyên
1. Làm quen với số nguyên âm
- Các số tự nhiên (khác 0) 1; 2; 3; 4; … còn được gọi là các số nguyên dương.
- Các số - 1; -2; -3; … gọi là các số nguyên âm.
- Tập hợp gồm các số nguyên âm, số 0 và số nguyên dương gọi là tập hợp số nguyên.
.
Chú ý:
Số 0 không là số nguyên âm, cũng không phải là số nguyên dương.
Đôi khi ta còn viết thêm dấu “+” ngay trước một số nguyên dương. Chẳng hạn số 6 còn được viết là +6 (đọc là “dương sáu”).
2. Thứ tự trong tập số nguyên
Trục số:
Ta biểu diễn các số 0; 1; 2; 3; 4; 5 … và các số nguyên âm -1; -2; -3; 4; 5… như sau:

+ Chiều từ trái sang phải là chiều dương, chiều ngược lại là chiều âm.
+ Điểm biểu diễn số nguyên a được gọi là điểm a.
+ Cho hai số nguyên a và b. Trên trục số, nếu điểm a nằm trước điểm b thì số a nhỏ hơn số b, kí hiệu a < b.
So sánh hai nguyên:
Mọi số nguyên âm đều nhỏ hơn 0, do đó nhỏ hơn mọi số nguyên dương.
Nếu a, b là hai số nguyên dương và a > b thì – a < - b.
II. Phép cộng và phép trừ số nguyên
1. Cộng hai số nguyên cùng dấu
Quy tắc cộng hai số nguyên âm
Muốn cộng hai số nguyên âm, ta cộng phần số tự nhiên của chúng với nhau rồi đặt dấu “-“ trước kết quả.
2. Cộng hai số nguyên khác dấu
Hai số đối nhau:
Hai số nguyên a và b được gọi là đối nhau nếu a và b nằm khác phía với điểm 0 và có cùng khoảng cách đến gốc 0.
Chú ý:
Ta quy ước số đối của 0 là chính nó.
Tổng của hai số đối nhau luôn bằng 0.
Quy tắc cộng hai số nguyên khác dấu:
+ Hai số nguyên đối nhau thì có tổng bằng 0.
+ Muốn cộng hai số nguyên khác dấu (không đối nhau), ta tìm hiệu hai phân số tự nhiên của chúng (số lớn trừ số nhỏ) rồi đặt trước hiệu tìm được dấu của số có phần số tự nhiên lớn hơn.
3. Tính chất của phép cộng
Phép cộng số nguyên có tính chất sau:
+ Giao hoán: a + b = b + a;
+ Kết hợp: (a + b) + c = a + (b + c).
4. Trừ hai số nguyên
Quy tắc trừ hai số nguyên
Muốn trừ số nguyên a cho số nguyên b, ta cộng số nguyên a với số đối của số nguyên b:
a – b = a + (-b).
III. Quy tắc dấu ngoặc
Bỏ dấu ngoặc trong trường hợp đơn giản
Các số âm (hay dương) trong một dãy tính thường được viết trong dấu ngoặc. Nhờ quy tắc cộng hay trừ số nguyên, ta có thể viết dãy tính dưới dạng không có dấu ngoặc.
Vì phép trừ chuyển được về phép cộng nên các dãy tính như trên cũng được gọi là một tổng.
Quy tắc dấu ngoặc:
Khi bỏ dấu ngoặc có dấu “+” đằng trước, ta giữ nguyên dấu của các số hạng trong ngoặc;
Khi bỏ dấu ngoặc có dấu “-” đằng trước, ta phải đổi dấu tất cả các số hạng trong dấu ngoặc: dấu “+” đổi thành “-” và dấu “-” đổi thành dấu “+”.
IV. Phép nhân số nguyên
1. Nhân hai số nguyên khác dấu
Quy tắc nhân hai số nguyên khác dấu
Muốn nhân hai số nguyên khác dấu, ta nhân phần số tự nhiên của hai số đó với nhau rồi đặt dấu “-” trước kết quả nhận được.
Nếu thì m.(-n) = (-n).m = - (m.n).
2. Nhân hai số nguyên cùng dấu
Quy tắc nhân hai số nguyên âm
Muốn nhân hai số nguyên âm, ta nhân phần số tự nhiên của hai số đó với nhau.
Nếu thì (-m).(-n) = (-n).(-m) = m.n.
3. Tính chất của phép nhân
Phép nhân các số nguyên có các tính chất:
Giao hoán: a.b = b.a;
Kết hợp: (a.b).c = a.(b.c);
Phân phối của phép nhân đối với phép cộng: a.(b + c) = a.b + a.c.
V. Phép chia hết. Ước và bội của một số nguyên
1. Phép chia hết
Cho với . Nếu có số nguyên q sao cho a = b.q thì ta có phép chia hết a:b = q (trong đó ta cũng gọi a là số bị chia, b là số chia và q là thương). Khi đó ta nói a chia hết cho b, kí hiệu a b.
2. Ước và bội
Khi a b , ta còn gọi a là một bội của b và b là một ước của a.
Nhận xét:
Nếu a là một bội của b thì –a cũng là một bội của b.
Nếu b là một ước của a thì – b cũng là một ước của a.
Bài tập
Bài 1. Dùng số âm để diễn tả các thông tin sau:
a) Ở nơi lạnh nhất thế giới, nhiệt độ có thể xuống đến 600C dưới 00C.
b) Do dịch bệnh, một công ty trong một tháng đã bị lỗ 2 triệu đồng.
Lời giải
a) Ở nơi lạnh nhất thế giới, nhiệt độ có thể xuống đến - 600C.
b) Do dịch bệnh, một công ty một tháng có – 2 triệu đồng.
Bài 2. Tính một cách hợp lí:
a) 15.(-236) + 15.235;
b) 237.(-28) + 28.137;
c) 38.(27 – 44) – 27.(38 – 44).
Lời giải
a) 15.(-236) + 15.235
= 15.[(-236) + 235]
= 15.(-1)
= -15.
b) 237.(-28) + 28.137
= (-237).28 + 28.137
= 28.[(-237) + 137]
= 28.(-100)
= -2 800.
c) 38.(27 – 44) – 27.(38 – 44).
= 38.27 – 38.44 – 27.38 + 27.44
= 38.27 – 27.38 – 38.44 + 27.44
= 0 + 44.(-38 + 27)
= 0 + 44.(-11)
= - 484.
Bài 3. Có hay không hai số nguyên a và b mà hiệu a – b :
a) Lớn hơn cả a và b?
b) Lớn hơn a nhưng nhỏ hơn b?
Lời giải
a) Có trường hợp a – b > a hoặc a – b > b
Ví dụ: a = 10 và b = - 15
Ta có a – b = 10 – (-15) = 10 + 15 = 25.
Khi đó 25 > 15 và 25 > - 15.
b) Có trường hợp hiệu a – b lớn hơn a nhưng nhỏ hơn b:
Ví dụ: a = - 3, b = -1, a – b = -3 – (-1) = -2 .
Vì -3 < -2 < -1 hay a < a – b < b.
B. Trắc nghiệm Bài tập cuối Chương 3 (Kết nối tri thức 2023) có đáp án
I. Nhận biết
Câu 1. Chọn phát biểu đúng trong số các câu sau:
(A) Tập hợp số nguyên được kí hiệu là .
(B) +2 không phải là một số tự nhiên.
(C) 4 không phải là một số nguyên.
(D) – 5 là một số nguyên.
Lời giải
(A) Tập hợp số nguyên được kí hiệu là Z. Nên A sai.
(B) + 2 là một số tự nhiên nên B sai.
(C) 4 là một số nguyên nên C sai.
(D) – 5 là một số nguyên âm nên – 5 là một số nguyên nên D đúng.
Đáp án: D
Câu 2. Trong các phát biểu sau đây, phát biểu nào sai?
(A) 3 > - 4.
(B) – 5 > - 9.
(C) – 1 < 0.
(D) – 9 > -8.
Lời giải Vì trên trục số điểm – 9 nằm bên trái -8 nên -9 < -8. Do đó D sai.
Đáp án: D
Câu 3. Tính các thương sau: (- 14):(- 7).
A. – 2
B. 2
C. 4
D. -4
Lời giải (- 14):(- 7) = 14 : 7 = 2.
Đáp án: B
II. Thông hiểu
Câu 1. Kết quả của phép tính: 25 – (9 – 10) + (28 – 4) là:
A. 50.
B. 2.
C. – 2.
D. 48.
Lời giải
25 – (9 – 10) + (28 – 4)
= 25 – (- 1) + 24
= 25 + 1 + 24
= 26 + 24
= 50.
Đáp án: A
Câu 2. Kết quả của phép tính: (- 4) . (+21) . (- 25) . (- 2) là:
A. 420. (B) 4 200. (C) – 4 200. (D) - 420.
Lời giải
(- 4) . (+21) . (- 25) . (- 2)
= [(-4) . (-25)] . [(+21) . (-2)] (tính chất giao hoán và kết hợp)
= 100 . (-42)
= - 4 200.
Đáp án: C
Câu 3. Tính: (- 45) – (27 – 8).
A. 64
B. -26
C. -64
D. 26
Lời giải (- 45) – (27 – 8) = (-45) – 19 = (-45) + (-19) = -64.
Đáp án: C
Câu 4. Tìm số nguyên x, thỏa mãn: x2 = 81
A. x = 9
B. x = -9
C. x = 9 hoặc x = -9
D. x = 3
Lời giải
x2 = 81
x2 = 92 hoặc x2 = (-9)2
x = 9 hoặc x = - 9.
Vậy x = 9 hoặc x = - 9.
Đáp án: C
Câu 5. Cho biết năm sinh của một số nhà toán học.
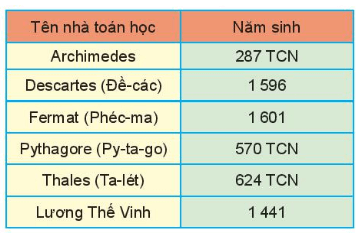
Em hãy sắp xếp các nhà toán học theo thứ tự giảm dần của năm sinh.
A. Fermat; Descartes; Lương thế Vinh; Archimedes; Pythagore; Thales
B. Fermat; Descartes; Lương thế Vinh; Pythagore; Thales; Archimedes
C. Fermat; Descartes; Lương thế Vinh; Thales; Pythagore; Archimedes
D. Fermat; Lương thế Vinh; Descartes; Thales; Pythagore; Archimedes
Lời giải
Archimedes có năm sinh 287 TCN nghĩa là năm thứ -287;
Pythagore có năm sinh 570 TCN nghĩa là năm thứ - 570;
Thales có năm sinh 624 TCN nghĩa là năm thứ - 624;
Ta có: 1 601 > 1 596 > 1 441 > - 287 > - 570 > - 624.
Các nhà bác học theo thứ tự năm sinh giảm dần: Fermat; Descartes; Lương thế Vinh; Archimedes; Pythagore; Thales.
Đáp án: A
Câu 6. Nhận xét nào sau đây đúng về kết quả của phép tính: (2 021 – 39) + [(-21) + (-61)];
A. Kết quả là một số nguyên âm
B. Kết quả là một số nguyên dương lớn hơn 2 000
C. Kết quả là một số nguyên dương nhỏ hơn 2 000
D. Kết quả bằng 0
Lời giải
(2 021 – 39) + [(-21) + (-61)]
= 2 021 + (-39) + (-21) + (-61)
= [2 021 + (-21)] + [(-39) + (-61)]
= 2 000 + (-100)
= 2 000 – 100
= 1 900 < 2 000
Đáp án: C
Xem thêm tóm tắt lý thuyết Toán lớp 6 sách Kết nối tri thức hay, chi tiết khác:
Lý thuyết Bài 18: Hình tam giác đều. Hình vuông. Hình lục giác đều
Lý thuyết Bài 19: Hình chữ nhật. Hình thoi. Hình bình hành. Hình thang cân
Lý thuyết Bài 20: Chu vi và diện tích của một số hình tứ giác đã học
Xem thêm các chương trình khác:
- Soạn văn lớp 6 (hay nhất) - Kết nối tri thức
- Soạn văn lớp 6 (ngắn nhất) - Kết nối tri thức
- Bộ câu hỏi ôn tập Ngữ văn lớp 6 - Kết nối tri thức
- Bố cục tác phẩm Ngữ văn 6 – Kết nối tri thức
- Nội dung chính tác phẩm Ngữ văn lớp 6 – Kết nối tri thức
- Tóm tắt tác phẩm Ngữ văn lớp 6 – Kết nối tri thức
- Tác giả tác phẩm Ngữ văn lớp 6 – Kết nối tri thức
- Văn mẫu lớp 6 – Kết nối tri thức
- Giải sgk Địa Lí 6 – Kết nối tri thức
- Giải sbt Địa Lí 6 – Kết nối tri thức
- Lý thuyết Địa Lí 6 – Kết nối tri thức
- Giải sgk Tin học 6 – Kết nối tri thức
- Giải sbt Tin học 6 – Kết nối tri thức
- Lý thuyết Tin học 6 – Kết nối tri thức
- Giải sgk Công nghệ 6 – Kết nối tri thức
- Giải sbt Công nghệ 6 – Kết nối tri thức
- Lý thuyết Công nghệ 6 – Kết nối tri thức
- Giải sgk Lịch sử 6 – Kết nối tri thức
- Giải sbt Lịch sử 6 – Kết nối tri thức
- Lý thuyết Lịch sử lớp 6 - Kết nối tri thức
- Giải sgk GDCD 6 – Kết nối tri thức
- Giải sbt GDCD 6 – Kết nối tri thức
- Lý thuyết GDCD 6 – Kết nối tri thức
- Giải sgk Khoa học tự nhiên 6 – Kết nối tri thức
- Giải sbt Khoa học tự nhiên 6 – Kết nối tri thức
- Lý thuyết Khoa học tự nhiên 6 – Kết nối tri thức
- Giải sgk Tiếng Anh 6 – Global Success
- Giải sbt Tiếng Anh 6 – Kết nối tri thức
- Bài tập Tiếng Anh 6 Global success theo Unit có đáp án
- Trọn bộ Từ vựng Tiếng Anh 6 Global success đầy đủ nhất
- Ngữ pháp Tiếng Anh 6 Global success
